ENT 281 Signal and Systems Lecture 3 Signal

ENT 281 Signal and Systems Lecture 3 Signal and Systems Modeling Concepts (Part 2) Dr. Abdul Halim Ismail 1 Semester 1, 2017/2018 Session

Contents 4 Elementary Signals 4. 1 Step Function 4. 2 Ramped Function 4. 3 Impulse Function 4. 4 Exponential Signal 4. 5 Sinusoidal Signal 5 System Block Diagram 6 Properties of the System 6. 1 Stability 6. 2 Memory 6. 3 Causality 6. 4 Inevitability 6. 5 Time Invariance 6. 6 Linearity School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 2

Contents 4 Elementary Signals 4. 1 Step Function 4. 2 Ramped Function 4. 3 Impulse Function 4. 4 Exponential Signal 4. 5 Sinusoidal Signal 5 System Block Diagram 6 Properties of the System 6. 1 Stability 6. 2 Memory 6. 3 Causality 6. 4 Inevitability 6. 5 Time Invariance 6. 6 Linearity School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 3

Elementary Signals The signals appear naturally in a wide class of physical systems. They serve as basic building blocks for the construction of more complex signal. -The Unit Step Function -The Ramp Function -The unit Impulse Function -Exponential signals -Sinusoidal Signals School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 4

Elementary Signals Unit Step Function The continuous-time version of the unit-step defined by: School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 5

Elementary Signals Unit Step Function (Signal Example 1) School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 6

Elementary Signals Unit Step Function (Signal Example 2) School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 7

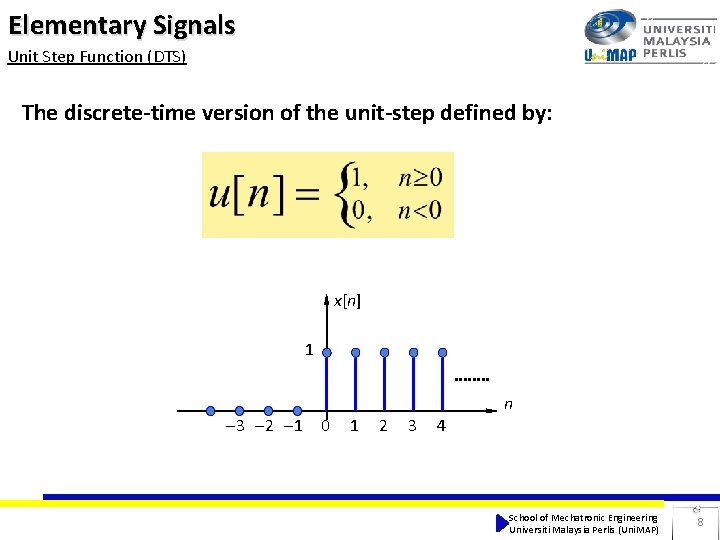
Elementary Signals Unit Step Function (DTS) The discrete-time version of the unit-step defined by: x[n] 1 3 2 1 n 0 1 2 3 4 School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 8

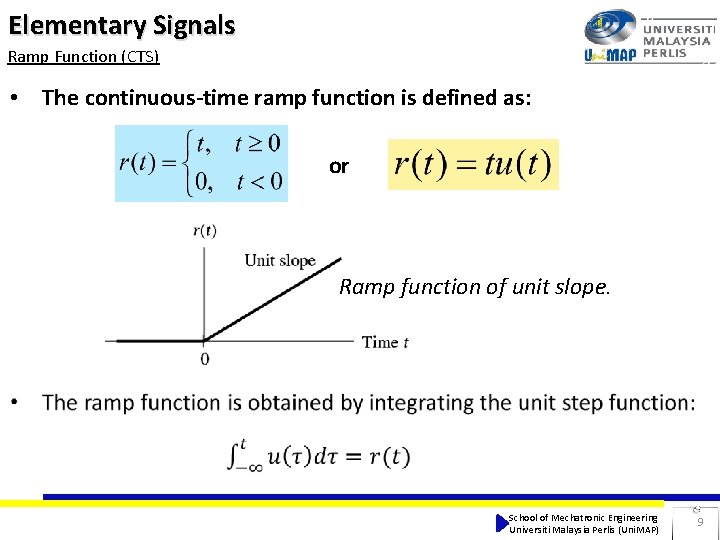
Elementary Signals Ramp Function (CTS) • The continuous-time ramp function is defined as: or Ramp function of unit slope. School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 9

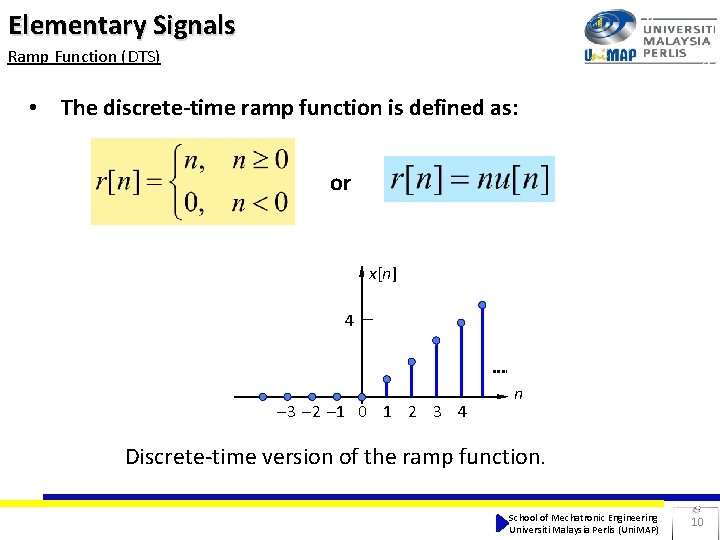
Elementary Signals Ramp Function (DTS) • The discrete-time ramp function is defined as: or x[n] 4 3 2 1 0 1 2 3 4 n Discrete-time version of the ramp function. School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 10

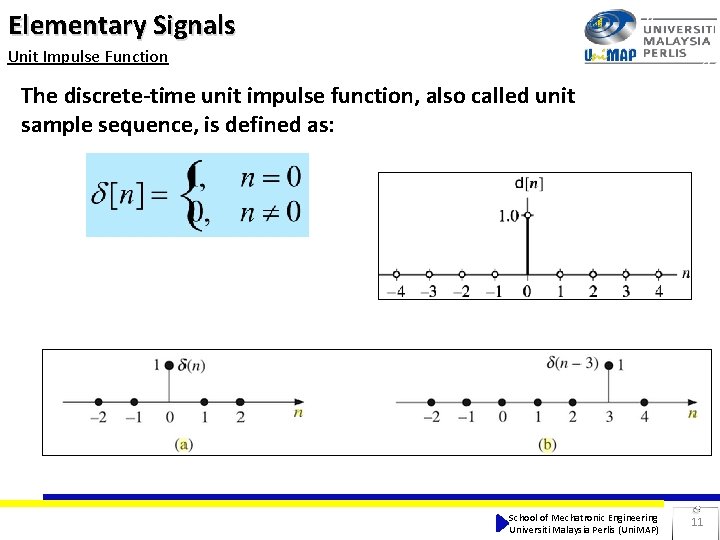
Elementary Signals Unit Impulse Function The discrete-time unit impulse function, also called unit sample sequence, is defined as: School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 11

Elementary Signals Unit Impulse Function The continuous-time unit impulse function δ(t), also called Dirac delta function. It is defined by: and School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 12

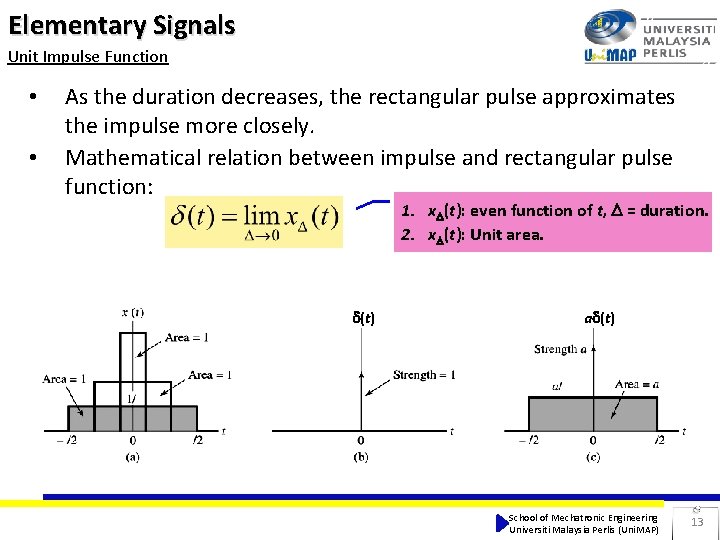
Elementary Signals Unit Impulse Function • • As the duration decreases, the rectangular pulse approximates the impulse more closely. Mathematical relation between impulse and rectangular pulse function: 1. x (t): even function of t, = duration. 2. x (t): Unit area. (t) a (t) Figure 1. 41 (p. 46) Discrete-time form of impulse. School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 13

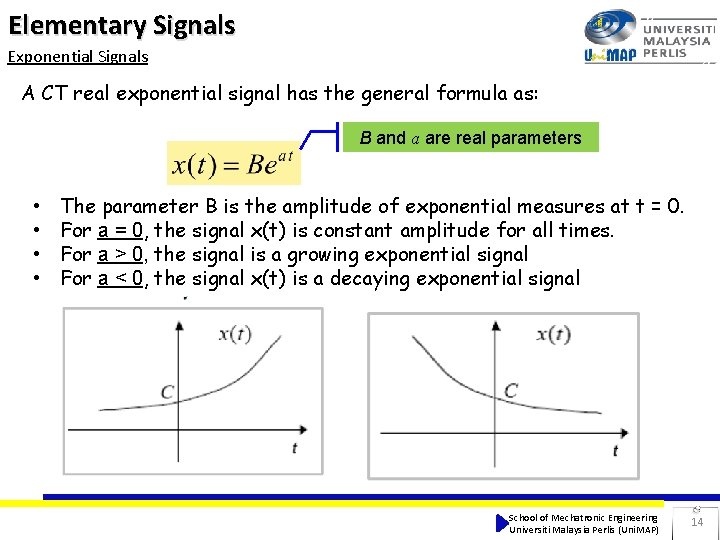
Elementary Signals Exponential Signals A CT real exponential signal has the general formula as: B and a are real parameters • • The parameter B is the amplitude of exponential measures at t = 0. For a = 0, the signal x(t) is constant amplitude for all times. For a > 0, the signal is a growing exponential signal For a < 0, the signal x(t) is a decaying exponential signal School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 14

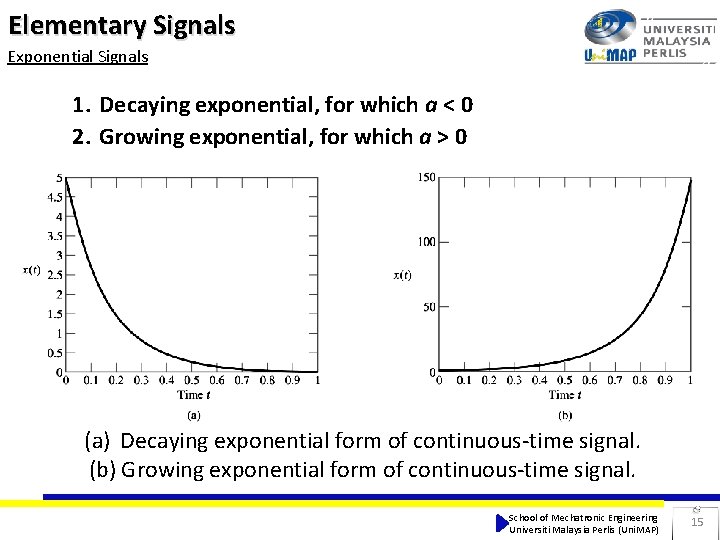
Elementary Signals Exponential Signals 1. Decaying exponential, for which a < 0 2. Growing exponential, for which a > 0 (a) Decaying exponential form of continuous-time signal. (b) Growing exponential form of continuous-time signal. School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 15

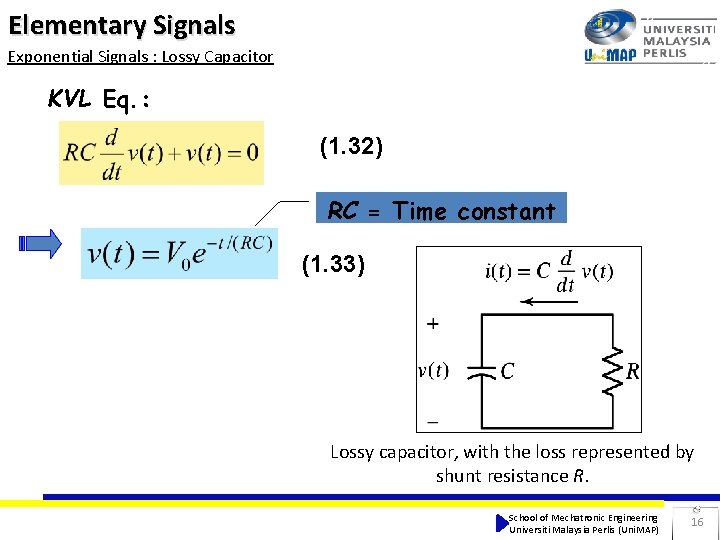
Elementary Signals Exponential Signals : Lossy Capacitor KVL Eq. : (1. 32) RC = Time constant (1. 33) Lossy capacitor, with the loss represented by shunt resistance R. School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 16

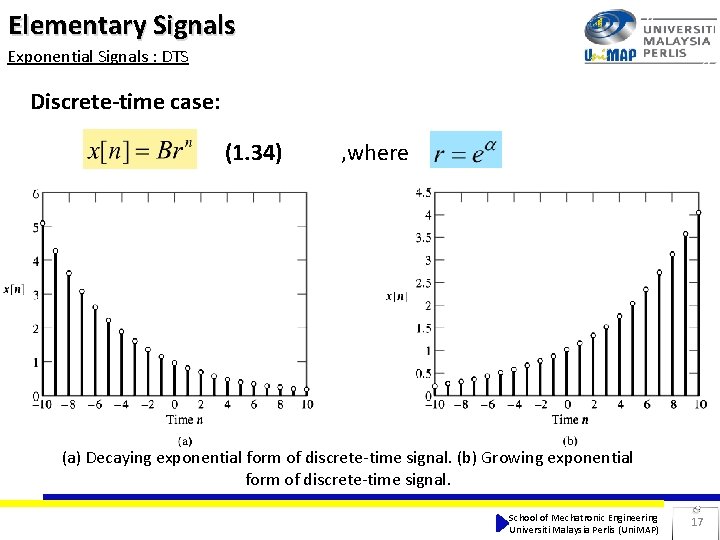
Elementary Signals Exponential Signals : DTS Discrete-time case: (1. 34) , where (a) Decaying exponential form of discrete-time signal. (b) Growing exponential form of discrete-time signal. School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 17

Elementary Signals Sinusoidal Signals ◆ Continuous-time case: (1. 35) where periodicity School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 18

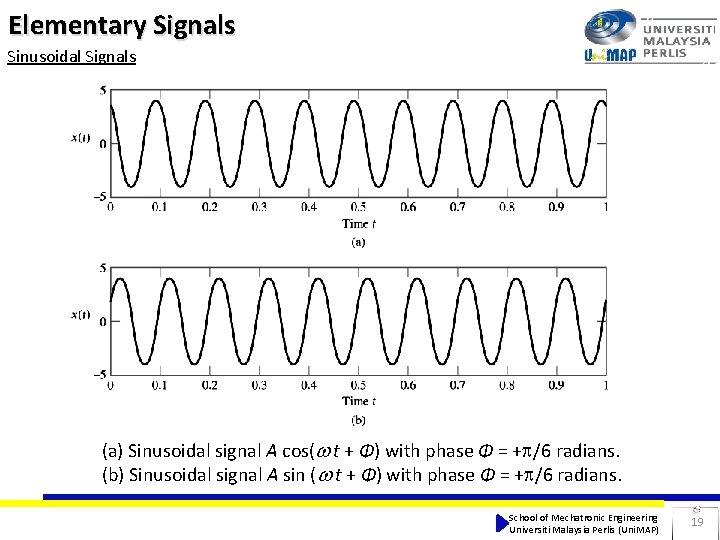
Elementary Signals Sinusoidal Signals (a) Sinusoidal signal A cos( t + Φ) with phase Φ = + /6 radians. (b) Sinusoidal signal A sin ( t + Φ) with phase Φ = + /6 radians. School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 19

Elementary Signals Sinusoidal Signals: Generation of Sinusoidal Signal Circuit Eq. : (1. 36) (1. 37) where Parallel LC circuit, assuming that the inductor L and capacitor C are both ideal. (1. 38) Natural angular frequency of oscillation of the circuit School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 20

Elementary Signals Sinusoidal Signals: DTS ◆ Discrete-time case : (1. 39) (1. 40) Periodic condition: or (1. 41) School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 21

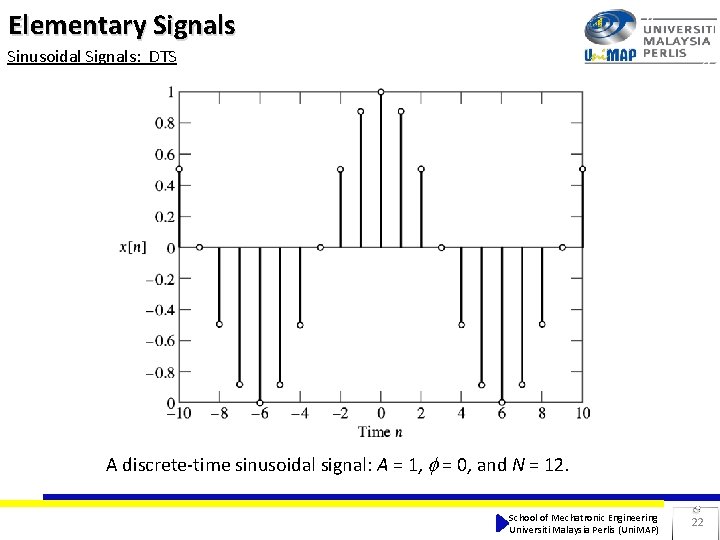
Elementary Signals Sinusoidal Signals: DTS A discrete-time sinusoidal signal: A = 1, = 0, and N = 12. School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 22

Elementary Signals Sinusoidal Signals: DTS Example 1. 7 Discrete-Time Sinusoidal Signal A pair of sinusoidal signals with a common angular frequency is defined by and (a)Both x 1[n] and x 2[n] are periodic. Find their common fundamental period. (b)Express the composite sinusoidal signal In the form y[n] = Acos( n + ), and evaluate the amplitude A and phase . School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 23

<Solution> (a) Angular frequency of both x 1[n] and x 2[n]: This can be only for m = 5, 10, 15, …, which results in N = 2, 4, 6, … (b) Trigonometric identity: Let = 5 , then compare x 1[n] + x 2[n] with the above equation to obtain that School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 24

f= /6 Accordingly, we may express y[n] as School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 25

Sinusoidal and Complex Exponential Signals Complex exponential signal: School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 26

Sinusoidal and Complex Exponential Signals 1. Continuous-time signal in terms of sine function: 2. Discrete-time case: and School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 27

Sinusoidal and Complex Exponential Signals 3. Two-dimensional representation of the complex exponential e j n for = /4 and n = 0, 1, 2, …, 7. Projection on real axis: cos( n); Projection on imaginary axis: sin( n) Complex plane, showing eight points uniformly distributed on the unit circle. School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 28

Contents 4 Elementary Signals 4. 1 Step Function 4. 2 Ramped Function 4. 3 Impulse Function 4. 4 Exponential Signal 4. 5 Sinusoidal Signal 5 System Block Diagram 6 Properties of the System 6. 1 Stability 6. 2 Memory 6. 3 Causality 6. 4 Inevitability 6. 5 Time Invariance 6. 6 Linearity School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 29

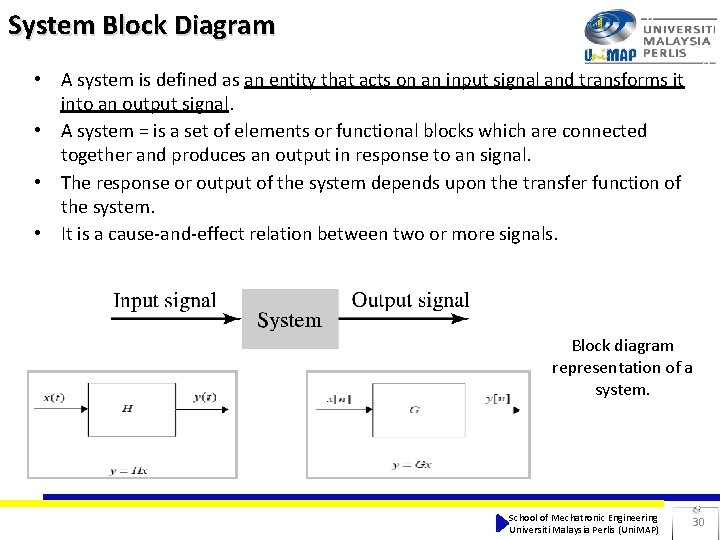
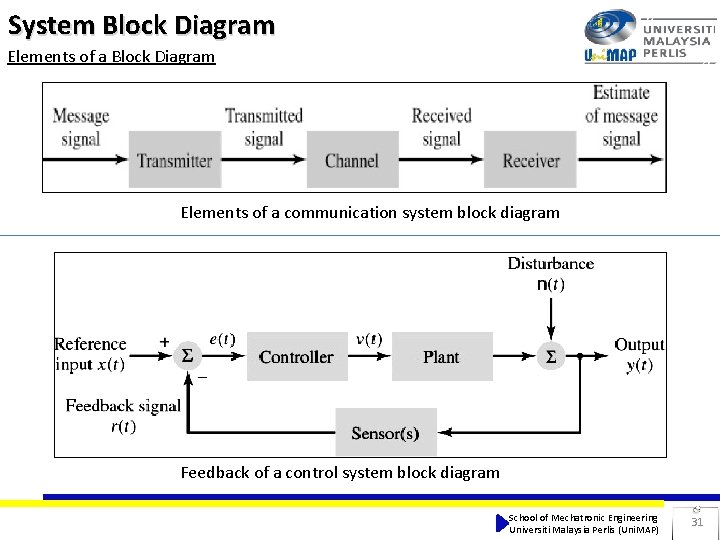
System Block Diagram • A system is defined as an entity that acts on an input signal and transforms it into an output signal. • A system = is a set of elements or functional blocks which are connected together and produces an output in response to an signal. • The response or output of the system depends upon the transfer function of the system. • It is a cause-and-effect relation between two or more signals. Block diagram representation of a system. School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 30

System Block Diagram Elements of a communication system block diagram Feedback of a control system block diagram School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 31

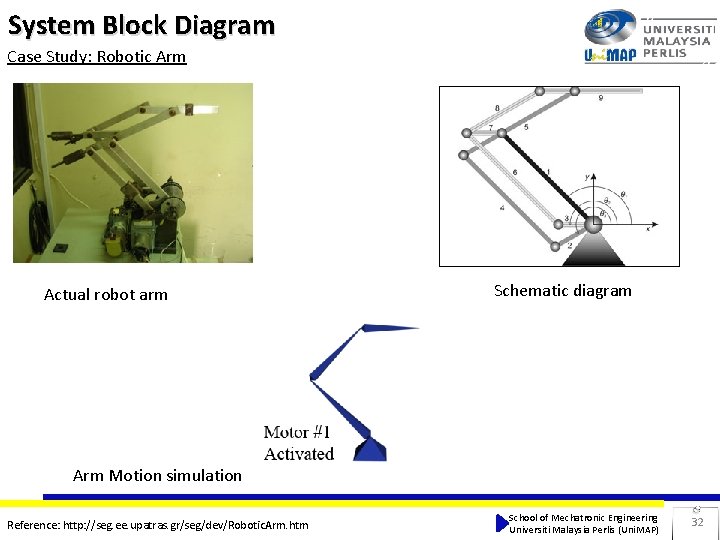
System Block Diagram Case Study: Robotic Arm Actual robot arm Schematic diagram Arm Motion simulation Reference: http: //seg. ee. upatras. gr/seg/dev/Robotic. Arm. htm School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 32

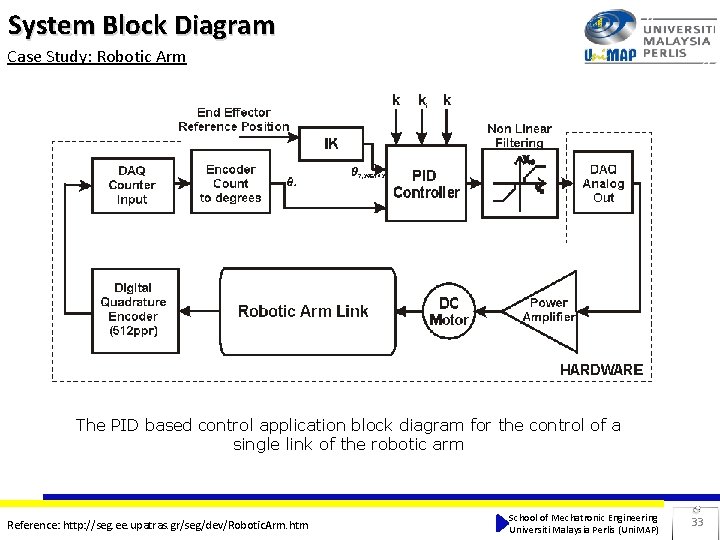
System Block Diagram Case Study: Robotic Arm The PID based control application block diagram for the control of a single link of the robotic arm Reference: http: //seg. ee. upatras. gr/seg/dev/Robotic. Arm. htm School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 33

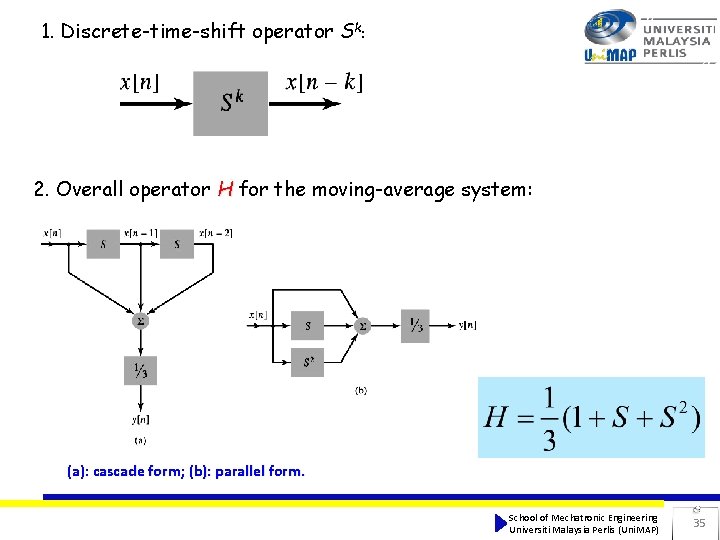
System Block Diagram Continuous-time and Discrete-time Example 1. 12 Moving-average system Consider a discrete-time system whose output signal y[n] is the average of the three most recent values of the input signal x[n], that is Formulate the operator H for this system; then, develop a block diagram representation for it. School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 34

1. Discrete-time-shift operator Sk: 2. Overall operator H for the moving-average system: (a): cascade form; (b): parallel form. School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 35

Contents 4 Elementary Signals 4. 1 Step Function 4. 2 Ramped Function 4. 3 Impulse Function 4. 4 Exponential Signal 4. 5 Sinusoidal Signal 5 System Block Diagram 6 Properties of the System 6. 1 Stability 6. 2 Memory 6. 3 Causality 6. 4 Inevitability 6. 5 Time Invariance 6. 6 Linearity School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 36

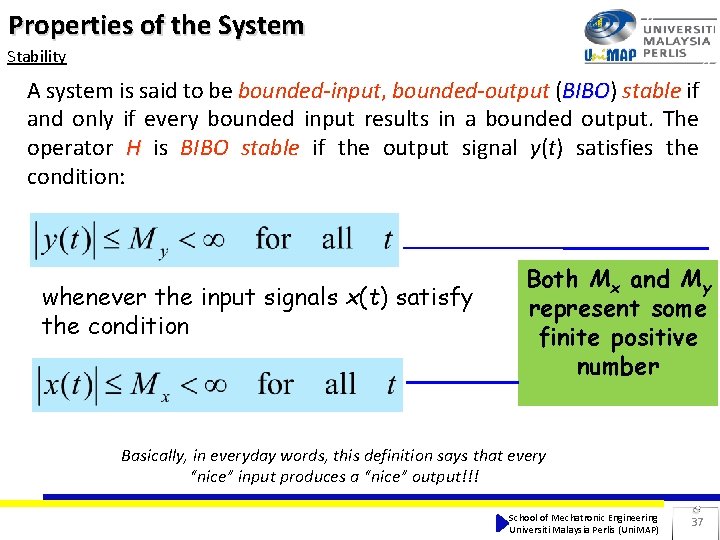
Properties of the System Stability A system is said to be bounded-input, bounded-output (BIBO) BIBO stable if and only if every bounded input results in a bounded output. The operator H is BIBO stable if the output signal y(t) satisfies the condition: whenever the input signals x(t) satisfy the condition Both Mx and My represent some finite positive number Basically, in everyday words, this definition says that every “nice” input produces a “nice” output!!! School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 37

Properties of the System Stability The collapse of the Tacoma Narrow suspension bridge on 7 Nov. 1940. School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 38

Properties of the System Stability (Example 1) Show that the moving-average system described in Example 1. 12 is BIBO stable. 1. Assume that: 2. Input-output relation: The moving-average system is stable. School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 39

Properties of the System Stability (Example 2) Consider a discrete-time system whose input-output relation is defined by where r > 1. Show that this system is unstable. 1. Assume that: 2. We find that: With r > 1, the multiplying factor rn diverges for increasing n. The system is unstable. School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 40

Properties of the System Memory • A system is said to possess memory if its output signal depends on past or future values of the input signal. • A system is said to possess memoryless if its output signal depends only on the present values of the input signal. Ex. : Inductor Ex. : Resistor Memory ! Memoryless ! Moving Average system. Memory or Memoryless? This system. Memory or Memoryless? School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 41

Properties of the System Causality From Meriam-Webster dictionary: Causality: the relation between a cause and its effect or between regularly correlated events or phenomena • A system is said to be causal if its present value of the output signal depends only on the present or past values of the input signal. • A system is said to be noncausal if its output signal depends on one or more future values of the input signal. Ex. : Moving-average system Causal ! Ex. : Moving-average system Noncausal ! A causal system must be capable of operating in real time. School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 42

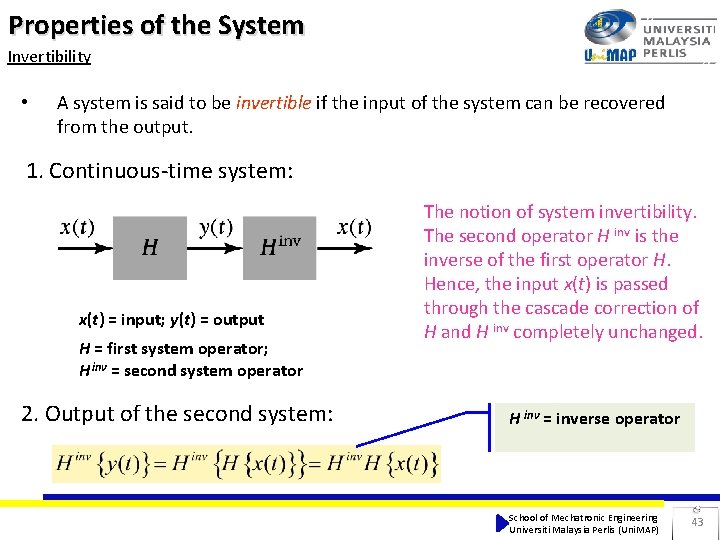
Properties of the System Invertibility • A system is said to be invertible if the input of the system can be recovered from the output. 1. Continuous-time system: x(t) = input; y(t) = output H = first system operator; H inv = second system operator 2. Output of the second system: The notion of system invertibility. The second operator H inv is the inverse of the first operator H. Hence, the input x(t) is passed through the cascade correction of H and H inv completely unchanged. H inv = inverse operator School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 43

3. Condition for invertible system: I = identity operator Example: Inverse of System Consider the time-shift system described by the input-output relation where the operator S t 0 represents a time shift of t 0 seconds. Find the inverse of this system. Sol. 1. Inverse operator S t 0: 2. Invertibility condition: Time shift of t 0 School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 44

Example: Non-Invertible System Show that a square-law system described by the input-output relation is not invertible. Sol. Since the distinct inputs x(t) and x(t) produce the same output y(t). Accordingly, the square-law system is not invertible. School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 45

Properties of the System Time Invariance • A system is said to be time invariance if a time delay or time advance of the input signal leads to an identical time shift in the output signal. A time-invariance system do not change with time. The notion of time invariance. (a) Time-shift operator St 0 preceding operator H. (b) Time-shift operator St 0 following operator H. These two situations are equivalent, provided that H is time invariant. School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 46

Properties of the System Time Invariance 1. Continuous-time system: 2. Input signal x 1(t) is shifted in time by t 0 seconds: S t 0 = operator of a time shift equal to t 0 3. Output of system H: 4. For Fig (b), the output of system H is y 1(t t 0): 5. Condition for time-invariant system: School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 47

Example: Inductor y 1(t) = i(t) The inductor shown in figure is described by the input-output relation: x 1(t) = v(t) where L is the inductance. Show that the inductor so described is time invariant. Solution: 1. Let x 1(t) x 1(t t 0) Response y 2(t) of the inductor to x 1(t t 0) is (A ) 2. Let y 1(t t 0) = the original output of the inductor, shifted by t 0 seconds: (B) 3. Changing variables: (A) Inductor is time invariant. School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 48

Example: Thermistor Let R(t) denote the resistance of thermistor, expressed as a function of time. We may express the input-output relation of the device as y 1(t) = i(t) x 1(t) = v(t) Show that thermistor so described is time variant. Solution: 1. Let response y 2(t) of thermistor to x 1(t t 0) is 2. Let y 1(t t 0) = the original output of thermistor due to x 1(t), shifted by t 0 seconds: 3. Since R(t) R(t t 0) Time variant! School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 49

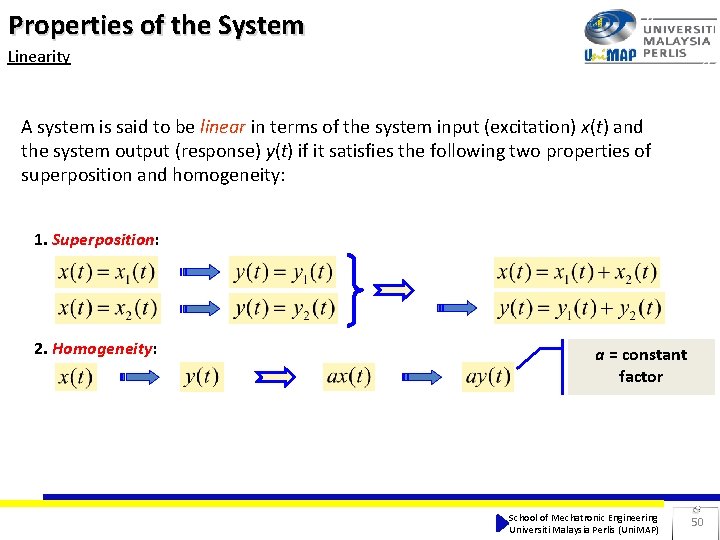
Properties of the System Linearity A system is said to be linear in terms of the system input (excitation) x(t) and the system output (response) y(t) if it satisfies the following two properties of superposition and homogeneity: 1. Superposition: 2. Homogeneity: a = constant factor School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 50

Properties of the System Linearity of a Continuous time system 1. Operator H represent the continuous-tome system. 2. Input: x 1(t), x 2(t), …, x. N(t) input signal; a 1, a 2, …, a. N Corresponding weighted factor 3. Output: Superposition and homogeneity where 4. Commutation and Linearity: School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 51

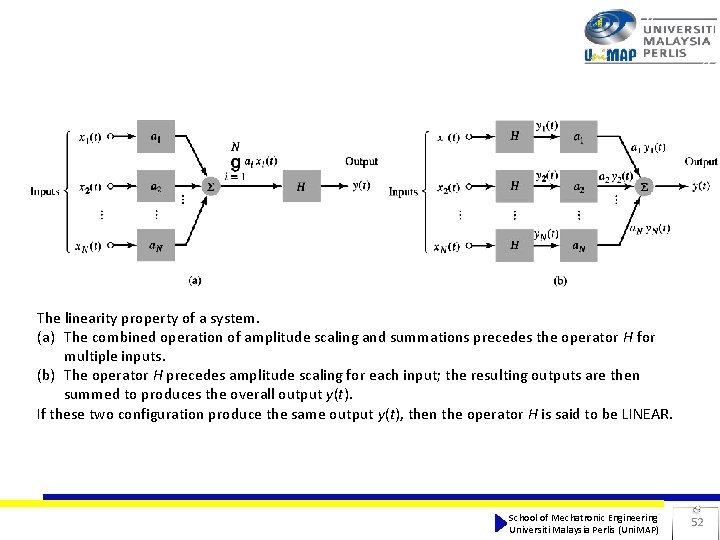
The linearity property of a system. (a) The combined operation of amplitude scaling and summations precedes the operator H for multiple inputs. (b) The operator H precedes amplitude scaling for each input; the resulting outputs are then summed to produces the overall output y(t). If these two configuration produce the same output y(t), then the operator H is said to be LINEAR. School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 52

Example: Linear Discrete-Time system Consider a discrete-time system described by the input-output relation Show that this system is linear. Solution 1. Input: 2. Resulting output signal: where Linear system! School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 53

Example: Nonlinear Continuous-Time System Consider a continuous-time system described by the input-output relation Show that this system is nonlinear. Solution: 1. Input: 2. Output: Here we cannot write Nonlinear system! School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 54

Contents 4 Elementary Signals 4. 1 Step Function 4. 2 Ramped Function 4. 3 Impulse Function 4. 4 Exponential Signal 4. 5 Sinusoidal Signal 5 System Block Diagram 6 Properties of the System 6. 1 Stability 6. 2 Memory 6. 3 Causality 6. 4 Inevitability 6. 5 Time Invariance 6. 6 Linearity 7 Noise School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 55

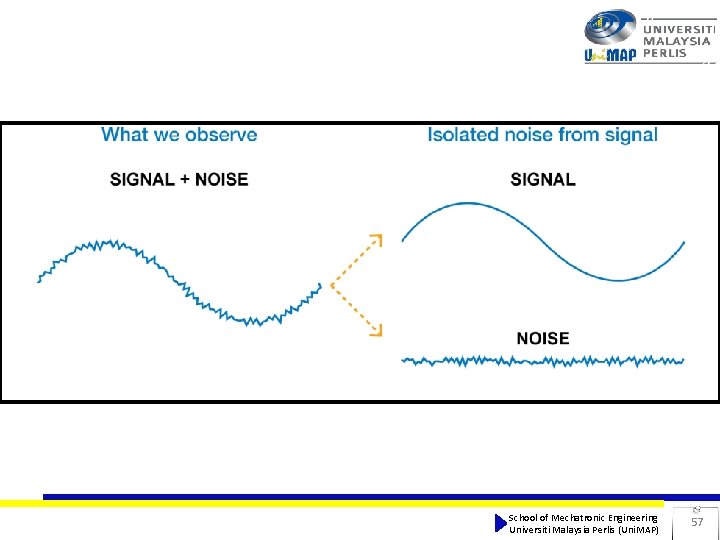
Noise Definition: an unwanted signal that tend to disturb the operation of a system, which are completely uncontrolled. Categories of noises: 1. External sources of noise: • Atmospheric noise, environmental noise, human-made noise 2. Internal sources of noise: • May arises inside the system • For example, ripples in electrical circuits, spontaneous fluctuations of current and voltages. School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 56

School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 57

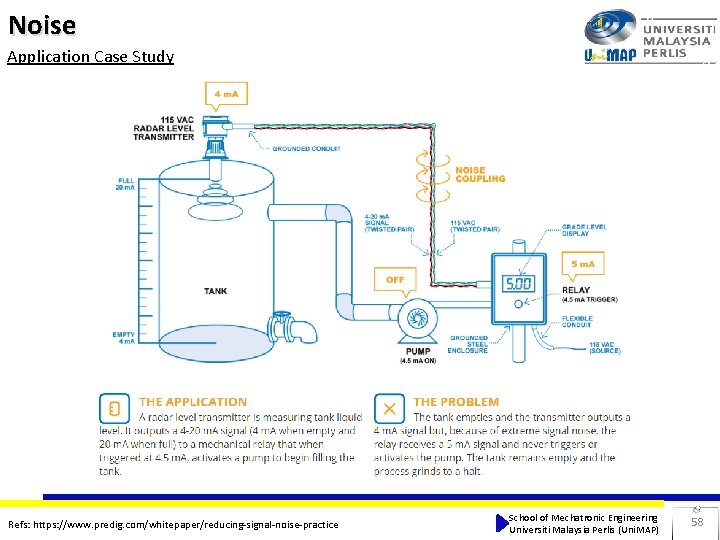
Noise Application Case Study Refs: https: //www. predig. com/whitepaper/reducing-signal-noise-practice School of Mechatronic Engineering Universiti Malaysia Perlis (Uni. MAP) 58