Ensino Superior Mecnica Vetorial para Engenheiros Dinmica 5

Ensino Superior Mecânica Vetorial para Engenheiros Dinâmica 5. 1 – Revisão de Estática e Dinâmica Amintas Paiva Afonso

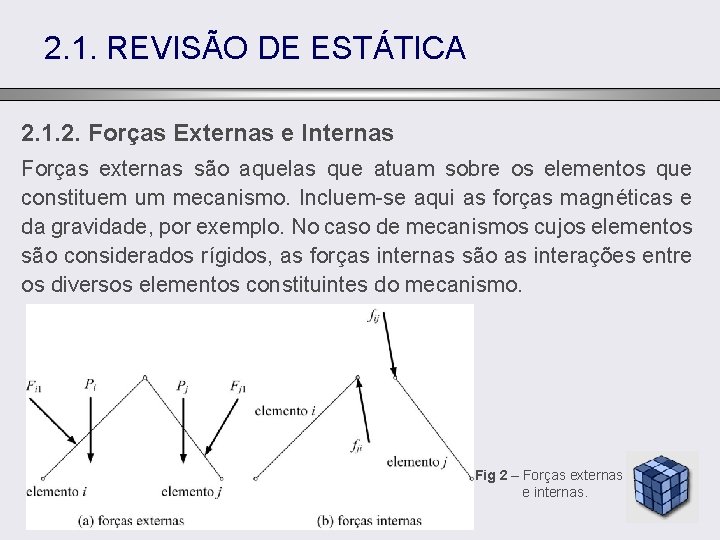
DIN MICA DE MECANISMOS Amintas Paiva Afonso

1. INTRODUÇÃO Enquanto a análise cinemática se ocupa da geometria dos movimentos utilizando as relações de deslocamento com tempo (velocidades e acelerações), a análise dinâmica diz respeito às questões de energia e potência necessárias para gerar o movimento pretendido (forças e momentos). A análise cinemática é importante na forma do movimento que determinado mecanismo deve desenvolver, sendo a base da síntese, que é o primeiro passo do projeto mecânico (design).

1. INTRODUÇÃO A importância da análise dinâmica reside na sua utilização para dimensionamento e escolha de material em determinado elemento ou dispositivo, necessários para que o mesmo possa resistir aos esforços a que estará submetido e à sua tarefa de transmitir potência. Os conhecimentos aqui desenvolvidos serão utilizados em cálculo de elementos de máquinas. Este estudo se restringe a mecanismos de movimento plano com um grau de mobilidade.

2. REVISÃO DE ESTÁTICA E DIN MICA Para que a análise dinâmica possa ser realizada, é necessário realizar uma breve revisão da estática a da dinâmica do corpo rígido. Revisão de Estática Os conceitos importantes da estática necessários são: - Descrição de Forças; - Tipos de Forças; - Equivalência de Forças; - Momentos e Torques; - Redução de um Sistema de Forças; - Leis da Estática e - Diagrama do Corpo Livre.

2. 1. REVISÃO DE ESTÁTICA 2. 1. 1. Descrição de Forças são grandezas vetoriais que representam a ação de um corpo sobre outro. As grandezas vetoriais são descritas pelo seu módulo, direção e reta de ação. Fig 1 – Descrição de força como grandeza vetorial.

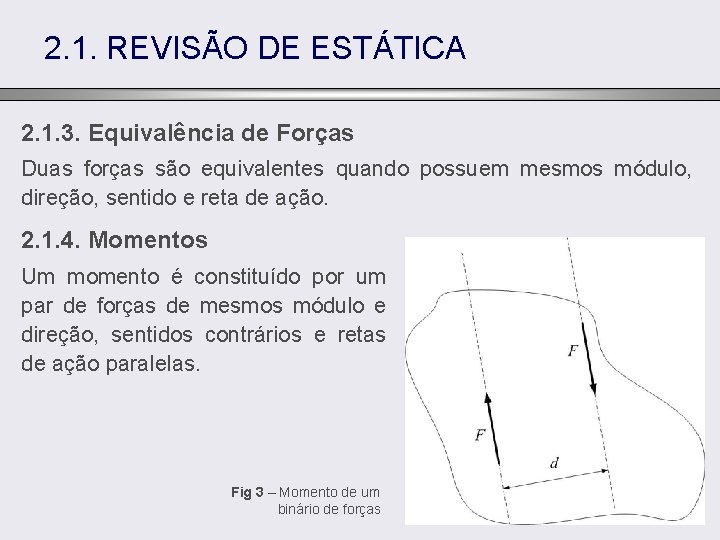
2. 1. REVISÃO DE ESTÁTICA 2. 1. 2. Forças Externas e Internas Forças externas são aquelas que atuam sobre os elementos que constituem um mecanismo. Incluem-se aqui as forças magnéticas e da gravidade, por exemplo. No caso de mecanismos cujos elementos são considerados rígidos, as forças internas são as interações entre os diversos elementos constituintes do mecanismo. Fig 2 – Forças externas e internas.

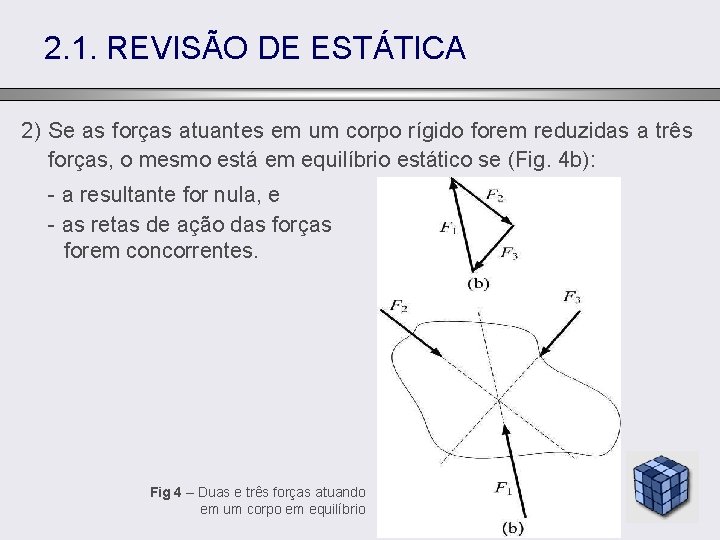
2. 1. REVISÃO DE ESTÁTICA 2. 1. 3. Equivalência de Forças Duas forças são equivalentes quando possuem mesmos módulo, direção, sentido e reta de ação. 2. 1. 4. Momentos Um momento é constituído por um par de forças de mesmos módulo e direção, sentidos contrários e retas de ação paralelas. Fig 3 – Momento de um binário de forças

2. 1. REVISÃO DE ESTÁTICA 2. 1. 5. Leis da Estática 1) Se as forças atuantes em um corpo rígido forem reduzidas a duas forças, o mesmo está em equilíbrio estático se estas forças forem (Fig. 4 a): 2) - colineares; 3) - de mesmo módulo; 4) - de sentidos opostos. Fig. 4 – Duas e três forças atuando em um corpo em equilíbrio

2. 1. REVISÃO DE ESTÁTICA 2) Se as forças atuantes em um corpo rígido forem reduzidas a três forças, o mesmo está em equilíbrio estático se (Fig. 4 b): - a resultante for nula, e - as retas de ação das forças forem concorrentes. Fig 4 – Duas e três forças atuando em um corpo em equilíbrio

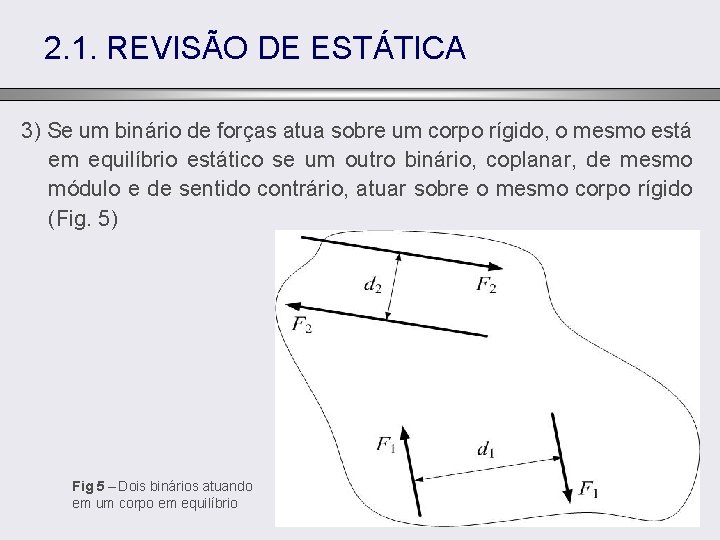
2. 1. REVISÃO DE ESTÁTICA 3) Se um binário de forças atua sobre um corpo rígido, o mesmo está em equilíbrio estático se um outro binário, coplanar, de mesmo módulo e de sentido contrário, atuar sobre o mesmo corpo rígido (Fig. 5) Fig 5 – Dois binários atuando em um corpo em equilíbrio

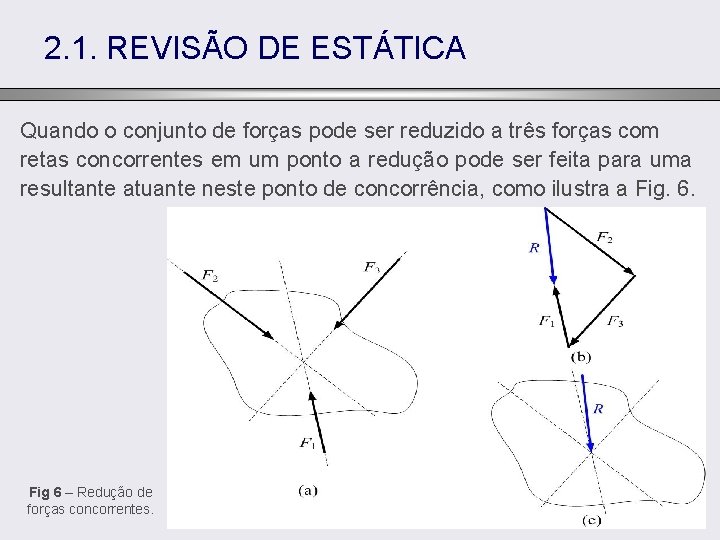
2. 1. REVISÃO DE ESTÁTICA Quando o conjunto de forças pode ser reduzido a três forças com retas concorrentes em um ponto a redução pode ser feita para uma resultante atuante neste ponto de concorrência, como ilustra a Fig. 6. Fig 6 – Redução de forças concorrentes.

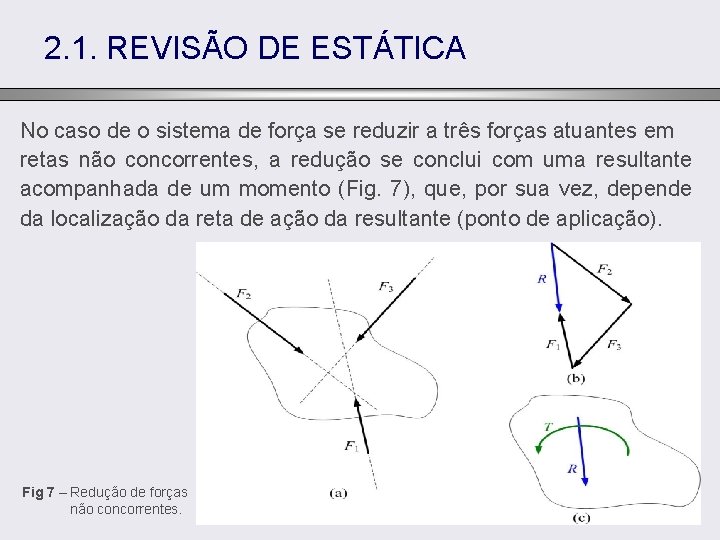
2. 1. REVISÃO DE ESTÁTICA No caso de o sistema de força se reduzir a três forças atuantes em retas não concorrentes, a redução se conclui com uma resultante acompanhada de um momento (Fig. 7), que, por sua vez, depende da localização da reta de ação da resultante (ponto de aplicação). Fig 7 – Redução de forças não concorrentes.

2. 1. REVISÃO DE ESTÁTICA 2. 1. 6. Condições de Equilíbrio Um corpo rígido está em equilíbrio estático se a resultante da soma vetorial das mesmas for nula e a soma vetorial dos momentos em relação a qualquer ponto também é nula. (1 a) (1 b)

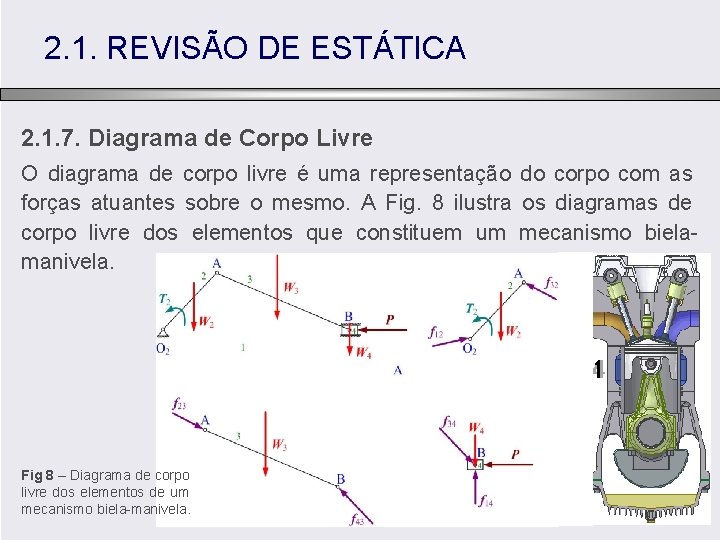
2. 1. REVISÃO DE ESTÁTICA 2. 1. 7. Diagrama de Corpo Livre O diagrama de corpo livre é uma representação do corpo com as forças atuantes sobre o mesmo. A Fig. 8 ilustra os diagramas de corpo livre dos elementos que constituem um mecanismo bielamanivela. Fig 8 – Diagrama de corpo livre dos elementos de um mecanismo biela-manivela.

2. 2. REVISÃO DE DIN MICA 2. 2. 1. Leis de Newton e Euler. Equilíbrio Dinâmico Leis de Newton 1ª Lei: Um corpo rígido permanece em equilíbrio (repouso ou movimento retilíneo uniforme) quando sobre ele não atuam forças externas. 2ª Lei: A razão de variação da quantidade de movimento de um corpo (linear e angular) é proporcional à força (ou momento) que sobre ela atua.

2. 2. REVISÃO DE DIN MICA Movimento de translação (2 a) Movimento de rotação (Lei de Euler) (2 b) onde Fi são as forças atuantes sobre o corpo (grandezas vetoriais são representadas em negrito), Ti os momentos destas forças em relação a um determinado ponto do plano, a a aceleração do centro de massa do corpo, a a aceleração angular do mesmo, m a sua massa e I o seu momento de inércia de massa em relação ao eixo de rotação. 3ª Lei: Quando ocorre a ação de uma força sobre um corpo, a esta ação sempre ocorre uma reação, igual em módulo, direção e com sentido contrário (o mesmo vale para momentos e movimentos angulares).

2. 2. REVISÃO DE DIN MICA 2. 2. 2. Princípio de D’Alembert. Forças e Conjugados de Inércia Princípio de D’Alembert Aplicando sobre o corpo rígido uma força F 0 = – ma e um conjugado T 0 = – I , o corpo estará em equilíbrio estático. Movimento de translação (3 a) Movimento de rotação (Lei de Euler) (3 b)

2. 2. REVISÃO DE DIN MICA Define-se então força de inércia e conjugado de inércia como Movimento de translação (4 a) Movimento de rotação (Lei de Euler) (4 b) O corpo rígido ilustrado na Fig 9 está em equilíbrio estático se e = T 0/F 0 = I /ma com T 0, F 0, e a sendo os módulos dos vetores correspondentes. Fig 9 – Princípio de D’Alembert - equilíbrio.

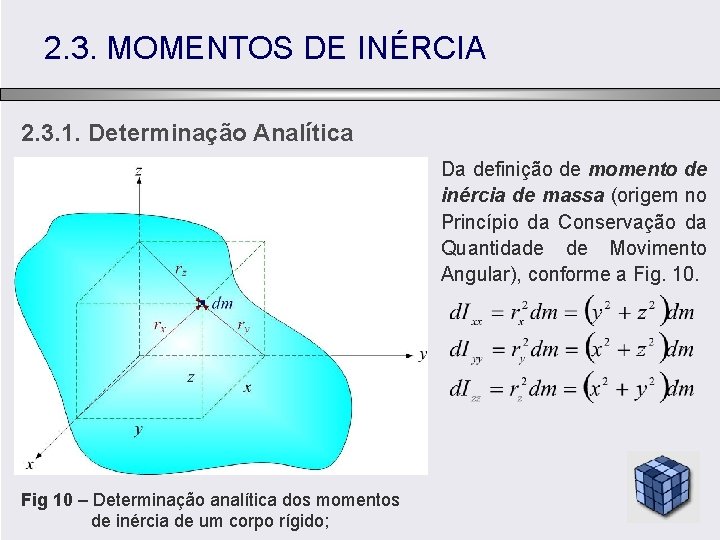
2. 3. MOMENTOS DE INÉRCIA 2. 3. 1. Determinação Analítica Da definição de momento de inércia de massa (origem no Princípio da Conservação da Quantidade de Movimento Angular), conforme a Fig. 10. Fig 10 – Determinação analítica dos momentos de inércia de um corpo rígido;