Enlargement Objectives F Grade Give a scale factor

Enlargement Objectives: F Grade Give a scale factor of an enlarged shape E Grade Enlarge a shape by a positive scale factor Find the measurements of the dimensions of an enlarged shape D Grade Enlarge a shape by a positive scale factor from a given centre C Grade Find the centre of enlargement

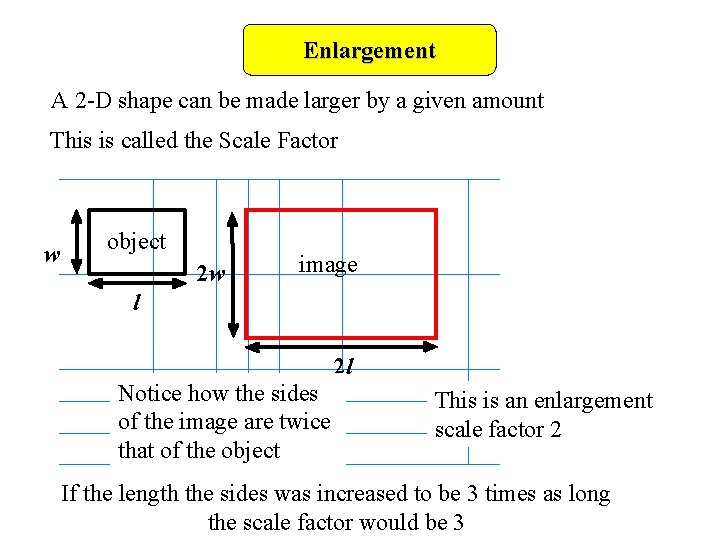
Enlargement A 2 -D shape can be made larger by a given amount This is called the Scale Factor w object 2 w image l 2 l Notice how the sides of the image are twice that of the object This is an enlargement scale factor 2 If the length the sides was increased to be 3 times as long the scale factor would be 3

Enlargement Objects can be enlarged using the scale factor to extend the length of the sides, because it is the sides that are increased it is called the linear scale factor. As was seen by finding the length of the image side by: image line length = object line length × scale factor similarly linear scale factor = object line length image line length This name is only important when the area and / or volume are part of the consideration for enlargement.

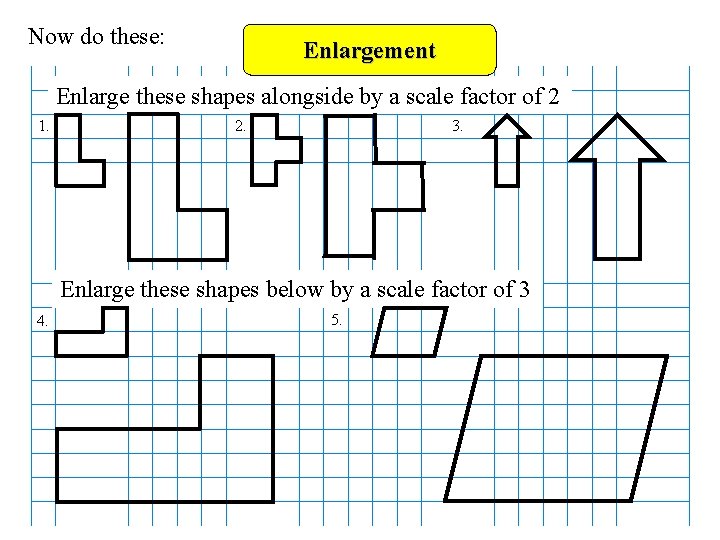
Now do these: Enlargement Enlarge these shapes alongside by a scale factor of 2 1. 3. 2. Enlarge these shapes below by a scale factor of 3 4. 5.

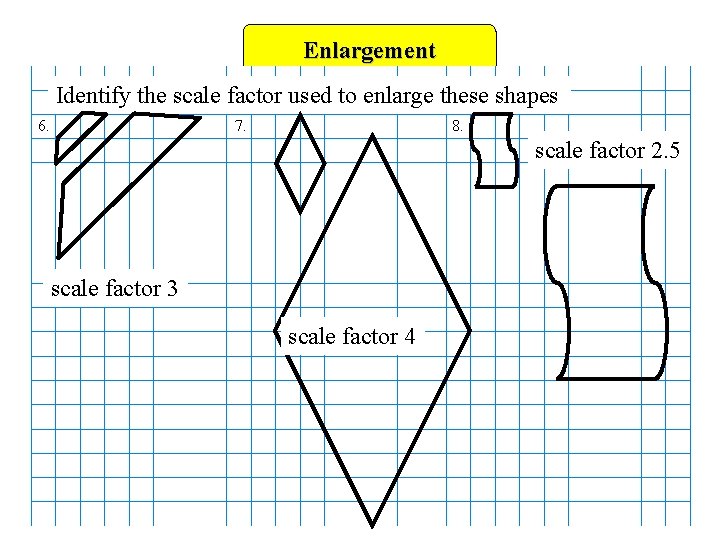
Enlargement Identify the scale factor used to enlarge these shapes 6. 8. 7. scale factor 2. 5 scale factor 3 scale factor 4

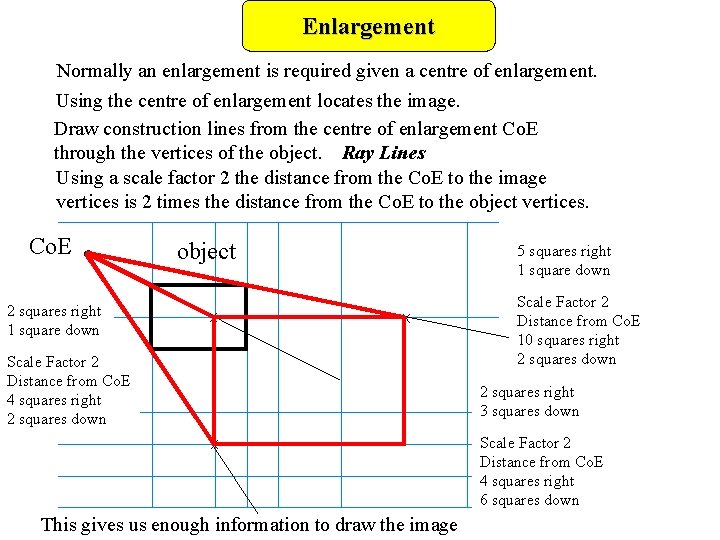
Enlargement Normally an enlargement is required given a centre of enlargement. Using the centre of enlargement locates the image. Draw construction lines from the centre of enlargement Co. E through the vertices of the object. Ray Lines Using a scale factor 2 the distance from the Co. E to the image vertices is 2 times the distance from the Co. E to the object vertices. Co. E 2 squares right 1 square down object x 5 squares right 1 square down x Scale Factor 2 Distance from Co. E 4 squares right 2 squares down Scale Factor 2 Distance from Co. E 10 squares right 2 squares down 2 squares right 3 squares down x This gives us enough information to draw the image Scale Factor 2 Distance from Co. E 4 squares right 6 squares down

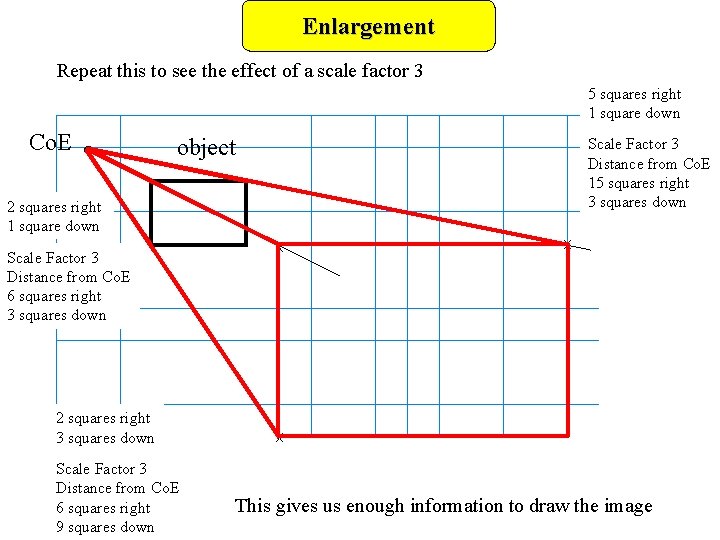
Enlargement Repeat this to see the effect of a scale factor 3 5 squares right 1 square down Co. E object Scale Factor 3 Distance from Co. E 15 squares right 3 squares down 2 squares right 1 square down Scale Factor 3 Distance from Co. E 6 squares right 3 squares down 2 squares right 3 squares down Scale Factor 3 Distance from Co. E 6 squares right 9 squares down x x x This gives us enough information to draw the image

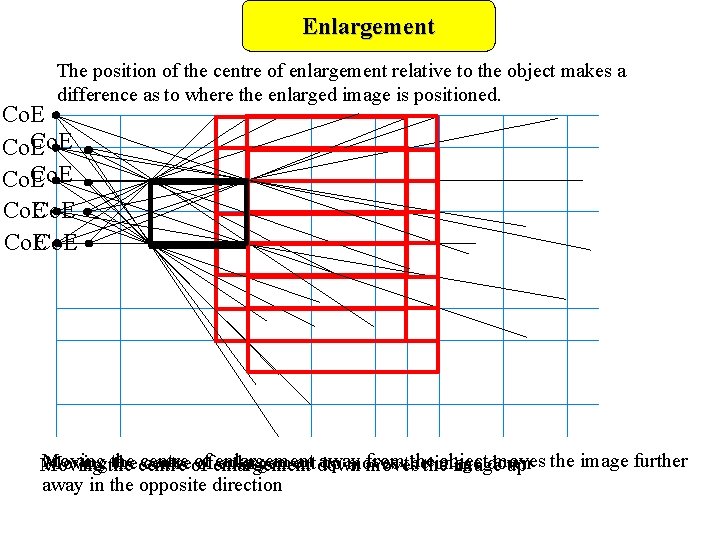
Enlargement The position of the centre of enlargement relative to the object makes a difference as to where the enlarged image is positioned. Co. ECo. E Moving the centre of enlargement away from the object moves Movingthe thecentreof ofenlargementdown up moves the image down Moving moves the image up the image further away in the opposite direction

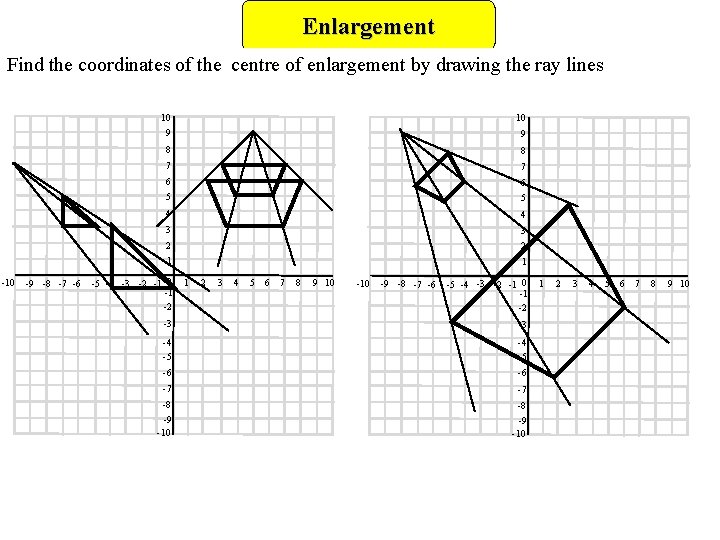
Enlargement Find the coordinates of the centre of enlargement by drawing the ray lines -10 -9 -8 -7 -6 10 10 9 9 8 8 7 7 6 6 5 5 4 4 3 3 2 2 1 1 -5 -4 -3 -2 -1 0 -1 -2 1 2 3 4 5 6 7 8 9 10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 -1 -2 -3 -3 -4 -5 -6 -6 -7 -7 -8 -8 -9 -10 1 2 3 4 5 6 7 8 9 10

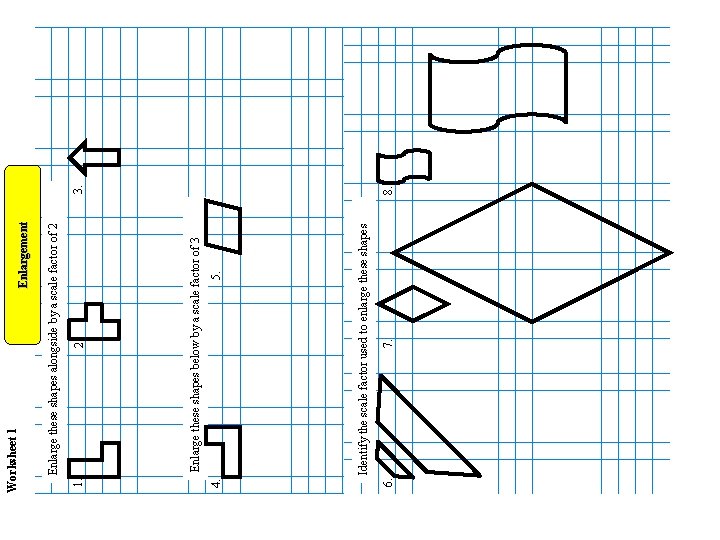
6. 4. 1. Enlargement 7. Identify the scale factor used to enlarge these shapes 5. Enlarge these shapes below by a scale factor of 3 2. Enlarge these shapes alongside by a scale factor of 2 Worksheet 1 8. 3.

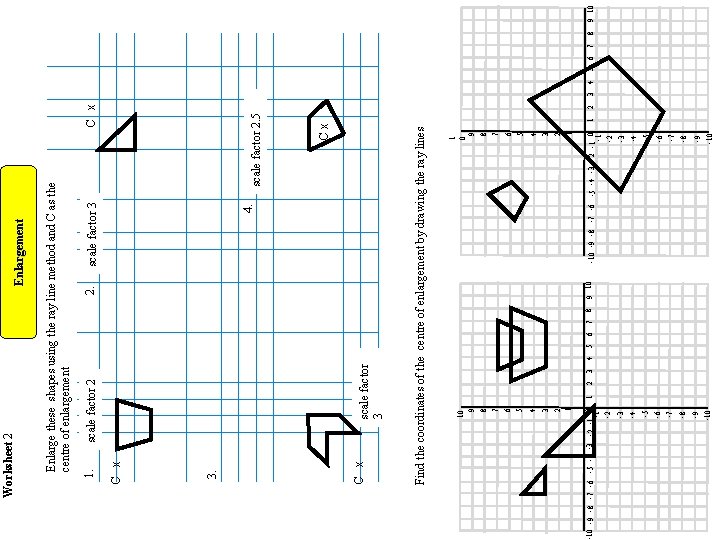
Enlargement scale factor 3 scale factor 2 2. 4. scale factor 3 Cx 3 4 5 6 7 8 9 10 -9 -10 -7 -8 -9 -7 -8 -6 -10 -5 -6 -5 -3 -4 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 -1 -2 -3 -4 3 2 1 4 5 3 6 5 6 2 7 7 1 1 0 9 8 1 scale factor 2. 5 2 C x Find the coordinates of the centre of enlargement by drawing the ray lines C x 3. C x 1. Enlarge these shapes using the ray line method and C as the centre of enlargement Worksheet 2 3 4 5 6 7 8 9 10