Engr 240 Week 14 Chapter 17 ImpulseMomentum Principle

Impulse-Momentum Principle For A Rigid Body For a system of particles: System Momenta 1

Impulse-Momentum Diagram For A Rigid Body . Three independent equations: Two summations of vector

CONSERVATION OF LINEAR MOMENTUM: When the vector sum of all linear impulses acting on

Example 1. Gear A has a mass of 10 kg and a radius of

Example 2. Two solid spheres of radius 3 in. , weighing 2 lb each,

Eccentric Impact Let A and B be the two points of contact during collision.

Example 3. A 0. 05 -lb bullet is fired into the side of a

Example 4. A 2 -kg sphere moving horizontally to the right with an initial

Slides: 9

Download presentation

Engr 240 – Week 14 Chapter 17. Impulse-Momentum Principle For A Rigid Body

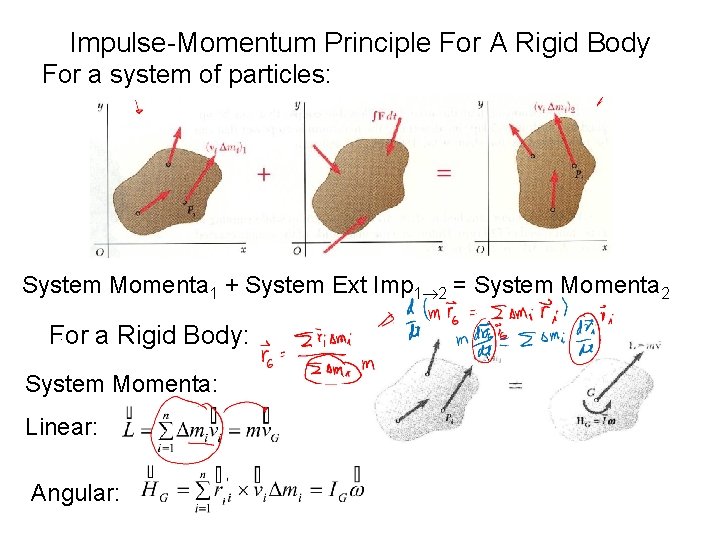
Impulse-Momentum Principle For A Rigid Body For a system of particles: System Momenta 1 + System Ext Imp 1 2 = System Momenta 2. For a Rigid Body: System Momenta: Linear: Angular:

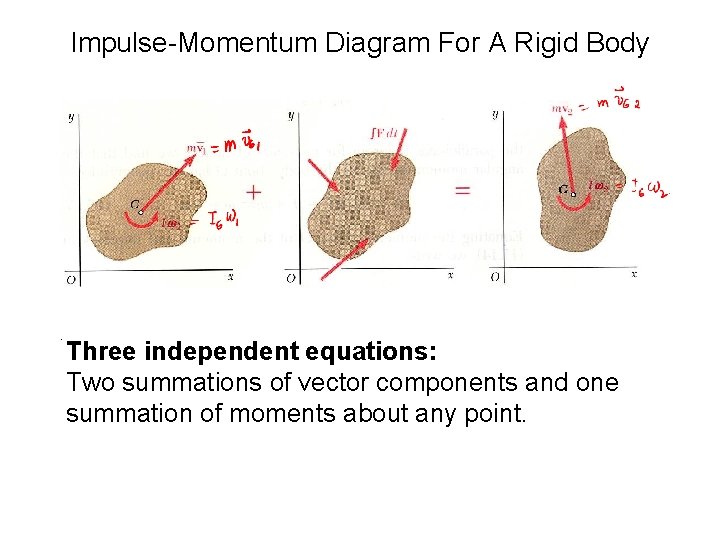
Impulse-Momentum Diagram For A Rigid Body . Three independent equations: Two summations of vector components and one summation of moments about any point.

CONSERVATION OF LINEAR MOMENTUM: When the vector sum of all linear impulses acting on the rigid body (i. e. , no net force): The velocity of the center of mass is constant. Angular velocity changes if there is a net moment of forces about G. CONSERVATION OF ANGULAR MOMENTUM: When the sum of angular impulses about point O is zero (e. g. , when the lines of action of all external forces pass through point O):

Example 1. Gear A has a mass of 10 kg and a radius of gyration of 200 mm, and gear B has a mass of 3 kg and a radius of gyration of 80 mm. The system is at rest when a couple M of magnitude 6 N-m is applied to gear B. Neglecting friction, determine (a) the time required for the angular velocity of gear B to reach 60 rpm, (b) the tangential force which gear B exerts on gear A.

Example 2. Two solid spheres of radius 3 in. , weighing 2 lb each, are mounted at A and B on the horizontal rod A’B’, which rotates freely about the vertical with a counterclockwise angular velocity of 6 rad/s. The spheres are held in position by a cord which is suddenly cut. Knowing that the centroidal moment of inertia of the rod and pivot is IG=0. 25 lb-ft-s 2, determine (a) the angular velocity of the rod after the spheres have moved to positions A’ and B’, (b) the energy lost due to the plastic impact of the spheres and the stops at A’ and B’.

Eccentric Impact Let A and B be the two points of contact during collision. The relative velocities of the two points of contact A and B are given by SOLVING AN IMPACT PROBLEM: 1. Draw diagrams: Syst Momenta 1 + Syst Ext Imp 1 2 = Syst Momenta 2 3 equations: 2 summation of components, and one moment summation 2. Reduce the number of unknowns using kinematic equations relating velocities of center of mass with angular velocities, and velocities of points of contact before and after impact.

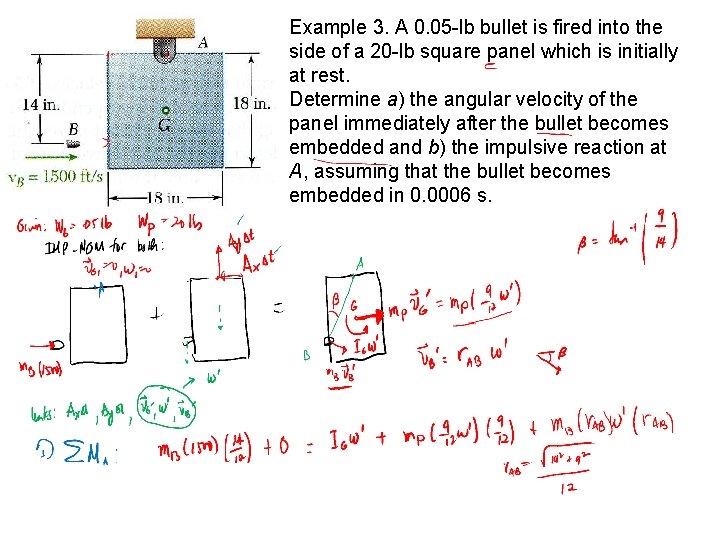
Example 3. A 0. 05 -lb bullet is fired into the side of a 20 -lb square panel which is initially at rest. Determine a) the angular velocity of the panel immediately after the bullet becomes embedded and b) the impulsive reaction at A, assuming that the bullet becomes embedded in 0. 0006 s.

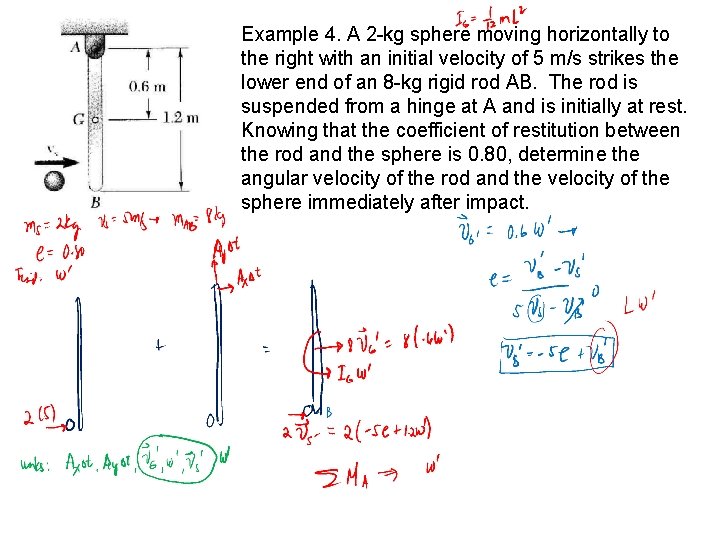
Example 4. A 2 -kg sphere moving horizontally to the right with an initial velocity of 5 m/s strikes the lower end of an 8 -kg rigid rod AB. The rod is suspended from a hinge at A and is initially at rest. Knowing that the coefficient of restitution between the rod and the sphere is 0. 80, determine the angular velocity of the rod and the velocity of the sphere immediately after impact.