Engineering Principles in Software Engineering five important concepts

Engineering Principles in Software Engineering five important concepts in CS that you will learn that can enhance software development

1. Divide-and-conquer • a general strategy for solving problems – an aspect of Computational Thinking – break problems into smaller sub-problems, which might be easier to solve (if decoupled) – example: chess moves • if I could just capture the opponents queen, then I could. . – or break large datasets into smaller pieces

• example: mergesort – given a list of numbers in random order – split the list into 2 halves – sort each half independently – merge the two sub-lists (interleave) 1 18 22 17 6 13 9 10 7 15 14 4 ← here is a list to sort 1 18 22 17 6 13 | 9 10 7 15 14 4 ← divide into 2 sub-lists 1 6 13 17 18 22 | 4 7 9 10 14 15 ← sort each separately 1 4 6 7 9 10 13 14 15 17 18 22 ← merge them back together

2. Recursion • a form of divide-and-conquer • write functions that call themselves call trace: • example: factorial fact(3) => n! = 1 x 2 x 3. . . n = n(n-1)! def fact(n): if n<=1: return 1 // base case return n*fact(n-1) fact(2) => fact(1) 1 <= 2*1=2<= 3*2=6 <= • example: mergesort – when you divide list into 2 halves, how do you sort each half – by calling mergesort, of course!

3. Greedy algorithms • most implementations involve making tradeoffs – we know NP-complete problems are hard and probably cannot be solved in polynomial time – use a heuristic/shortcut – might get a pretty good solution (but not optimal) in faster time • greedy methods do not guarantee an optimal solution – however, in many cases, a near-optimal solution can be good enough – it is important to know when a heuristic will NOT produce an optimal solution, and to know how suboptimal it is (i. e. an “error bound”)

• Examples of greedy algorithms – navigation, packet routing, shortest path in graph, robot motion planning • choose the “closest” neighbor in the direction of the destination – document comparison (e. g. diff) • start by aligning the longest matching substrings . . out to be more efficient to find the length of the longest subsequence. Then in the case where the. . increase the efficiency using the length of the longest subsequence. But if the first characters diffe – knapsack packing • choose item with highest value/weight ratio first – scheduling • schedule the longest job first, (or the one with most constraints)

4. Caching • One way to improve the efficiency of many programs is to use caching – saving intermediate results in memory that will get used multiple times – why calculate the same thing multiple times? – might require designing a special data structure (e. g. a hash table) to store/retrieve these efficiently – amortization: the cost of calculating something gets divided over all the times it is used

• calculating Fibonacci numbers – F(n) = F(n-1)+F(n-2) – base cases: F(1) = F(2) = 1 – this sequence of numbers arises in several patterns in nature, as well as the stock market – 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144. . . – (show calculating this slows down, and can be dramatically speeded up by caching results of previous function calls)

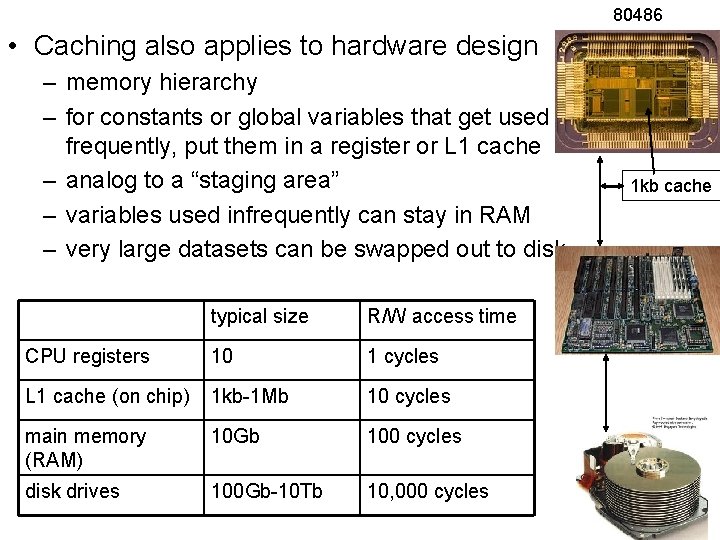
80486 • Caching also applies to hardware design – memory hierarchy – for constants or global variables that get used frequently, put them in a register or L 1 cache – analog to a “staging area” – variables used infrequently can stay in RAM – very large datasets can be swapped out to disk typical size R/W access time CPU registers 10 1 cycles L 1 cache (on chip) 1 kb-1 Mb 10 cycles main memory (RAM) 10 Gb 100 cycles disk drives 100 Gb-10 Tb 10, 000 cycles 1 kb cache

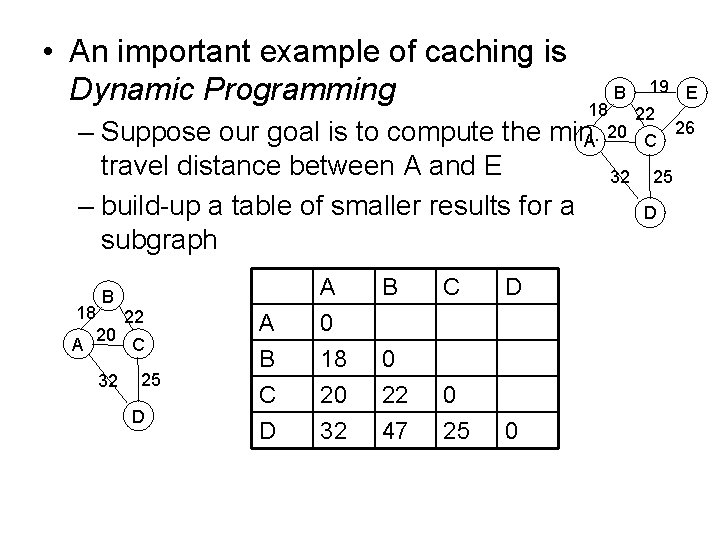
• An important example of caching is Dynamic Programming 19 E 18 22 26 20 min. A C – Suppose our goal is to compute the travel distance between A and E – build-up a table of smaller results for a subgraph B C A 0 18 20 0 22 0 D 32 47 25 B 18 22 20 A C 32 25 D D 0 B 32 25 D

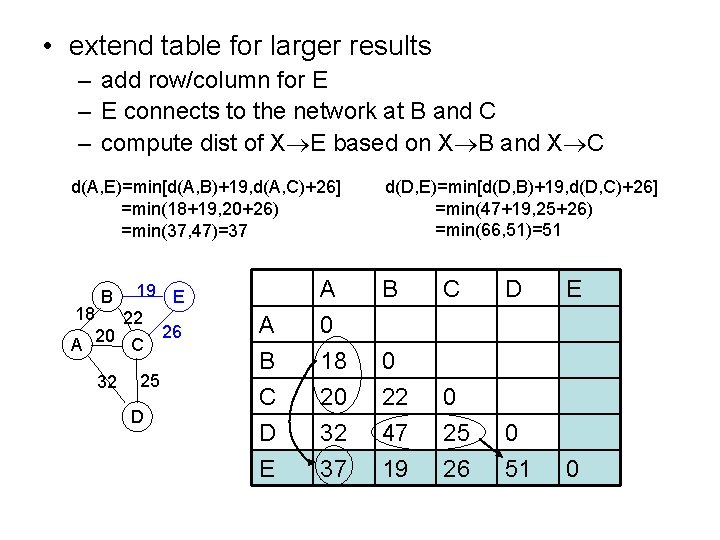
• extend table for larger results – add row/column for E – E connects to the network at B and C – compute dist of X E based on X B and X C d(A, E)=min[d(A, B)+19, d(A, C)+26] =min(18+19, 20+26) =min(37, 47)=37 19 E 18 22 26 20 A C B C A 0 18 20 0 22 0 D E 32 37 47 19 25 26 B 32 25 D d(D, E)=min[d(D, B)+19, d(D, C)+26] =min(47+19, 25+26) =min(66, 51)=51 D E 0 51 0

5. Abstraction and Reuse • Abstraction is the key to becoming a good programmer – don’t reinvent the wheel – more importantly, reuse things that have already been tested and debugged • This is the basis of Object-Oriented Programming

• Many large software projects are built by plugging components together • write a small amount of (“glue”) code the makes things work together • example: creating a web browser out of: a) an HTML text parser b) a display engine (graphics, windows) c) URL query/retrieval network functions d) plug-ins

Examples of Abstraction • Making a function out of things you do repeatedly – parameterizing it so it can be applied to a wider range of inputs

Here is output for scores of Aggies in basketball games so far this year: Here is code for printing a histogram of basketball scores (which typically range between 50 and 100 points): histo([82, 91, 68, 75, 79, 88, 67, 52, 74, 73, 52, 41, 63, 69, 57, 75, 72, 51, 5 5, 52, 36, 72]) def histo(Scores): i = 50 while i<100: c = 0 for s in Scores: if s i and s<i+5: c += 1 print i, ’*’*c i += 5 50 55 60 65 70 75 80 85 90 95 **** **** * * *

Suppose we want to generalize this code for printing a histogram of football scores too, which span a different range. Add parameters of lower and upper bound of histogram A and B, and step size S. def histo(Scores, A, B, S): i = A while i<B: c = 0 for s in Scores: if s i and s<i+S: c += 1 print i, ’*’*c i += S Here is output for scores of Aggies in football games last year: histo([52, 65, 42, 45, 41, 56, 57, 51, 10, 21, 52], A=0, B=70, S=10) 0 10 20 30 40 50 60 * * ***** * vs Rice W 52 -31 vs Sam Houston W 65 -28 vs #1 Alabama L 49 -42 vs SMU W 42 -13 @ Arkansas W 45 -33 @ Ole Miss W 41 -38 vs #24 Auburn L 45 -41 vs Vanderbilt W 56 -24 vs UTEP W 57 -7 vs Mississippi St W 51 -41 @ #22 LSU L 34 -10 @ #5 Missouri L 28 -21 vs #24 Duke* W 52 -48

• Object-oriented classes – encapsulation – define internal representation of data – interface – define methods, services – good design – make the external operations independent of the internal representation (helps decouple code) – example: a Complex number is a ‘thing’ that can be added/subtracted, multiplied (by another Complex or a scalar), conjugated, viewed as (a+bi) or (reiq)

• Here is an example of class definition of Complex Numbers in C++ class Complex { double re, im; // interval variables public: // constructor (initialization) Complex(double x, double y) { re = x; im = y; } void conjugate() { im *= -1; } double magnitude() { double z=re*re+im*im; return sqrt(z); } void print() { cout << "(" << re << "+" << im << "i)"; } }; A Complex object representing 1+2 i has two member variables for holding the real and imaginary components. re=1. 0 im=2. 0

#include <iostream> #include <iomanip> #include <math. h> using namespace std; class Complex {. . . from previous slide. . . }; int main() { Complex p=Complex(1, 2); cout << “|p|=“ << p. magnitude() << "n"; Complex p 2=p+p; // custom addition } Note how we get the magnitude of a Complex object by invoking a method on it, p. magnitude(). The calculation is done internally to the object. Output: > g++ complex. cpp –o complex -lm > complex p = (1. 0+2. 0 i) |p| = 2. 23607

• Templates in C++ – if you can sort a list of integers, why not generalize it to sort lists with any data type that can be pairwise-compared (total order)? void insertion. Sort(int a[], int n) { for (int i = 1; i <= n; i++) { int temp = a[i]; for (int j=i; j>0; j--) if(temp < a[j-1]) a[j] = a[j-1]; else break; a[j] = temp; } } 1 3 5 2 6 4 9 8 7 1 2 3 5 6 4 9 8 7 1 2 3 4 5 6 9 8 7

• Templates in C++ – can use same algorithm to sort any type T, as long as element can be compare with ‘<‘ operator – works on float, characters, strings. . . template <class T> void insertion. Sort(T a[], int n) { for(int i = 1; i <= n; i++) { T temp = a[i]; for (int j=i; j>0; j--) if(temp < a[j-1]) a[j] = a[j-1]; else break; a[j] = temp; } defined for string, characters, floats. . . }

• API design – Application-Programmer Interface – a coherent, complete, logical system of functions and data formats – example: OCR (optical character recognition) – you don’t want to have to implement feature-based character recognition that is font- and scaleindependent yourself (probably) – interface defines input (e. g. scanned TIFF images) and output (e. g. ASCII strings) String* OCRscan(Tiff. Image* input_image) – are you going to indicate coordinates where word was found on the page? – is the user able to load different character sets (alphabets)?

Engineering Principles in Software Engineering A summary of the key ideas we talked about. . . 1. divide-and-conquer 2. recursion 3. greedy algorithms, tradeoffs 4. caching, dynamic programming 5. abstraction and reuse