Engineering Physics Diffraction Diffraction of ocean water waves

Engineering Physics

Diffraction

Diffraction of ocean water waves Ocean waves passing through slits in Tel Aviv, Israel Diffraction occurs for all waves, whatever the phenomenon.

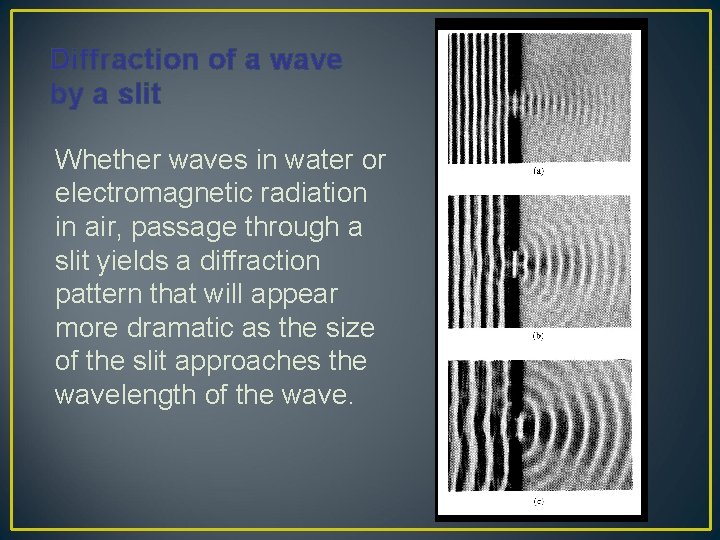
Diffraction of a wave by a slit Whether waves in water or electromagnetic radiation in air, passage through a slit yields a diffraction pattern that will appear more dramatic as the size of the slit approaches the wavelength of the wave.

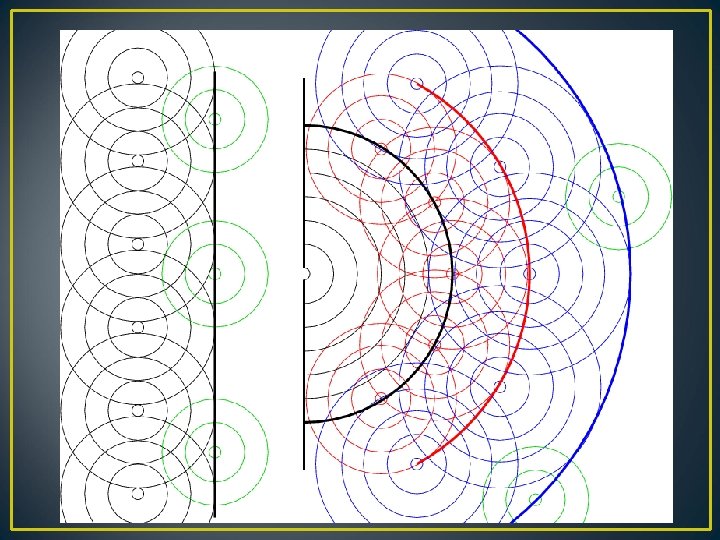
• In addition to interference, waves also exhibit another property – diffraction. • It is the bending of the waves as they pass by some objects or through an aperture. • The phenomenon of diffraction can be understood using Huygens principle

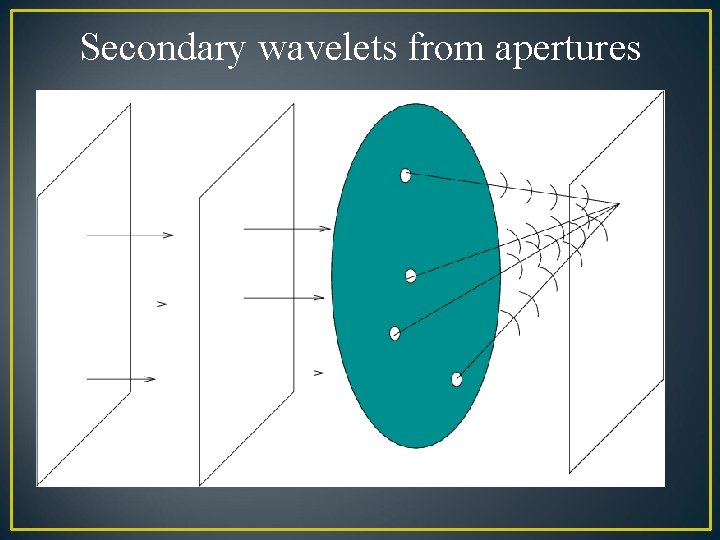
Huygen’s Principle • Every unobstructed point on a wavefront will act as a source of secondary spherical waves. • The new wavefront is the surface tangent to all the secondary spherical waves.

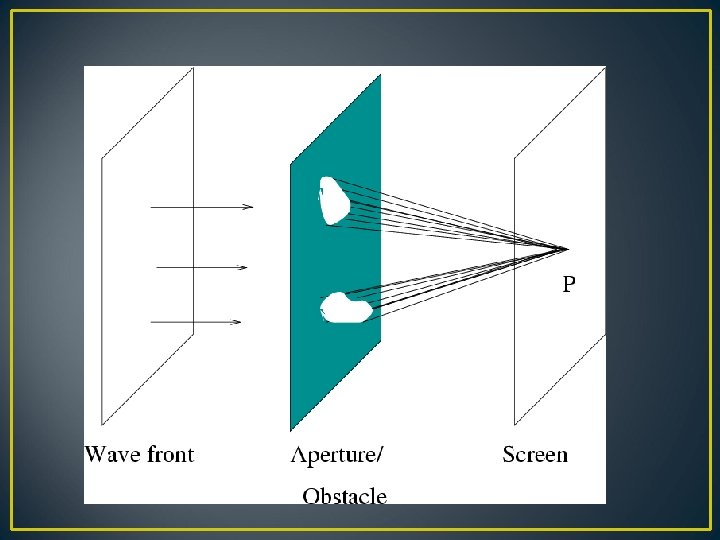
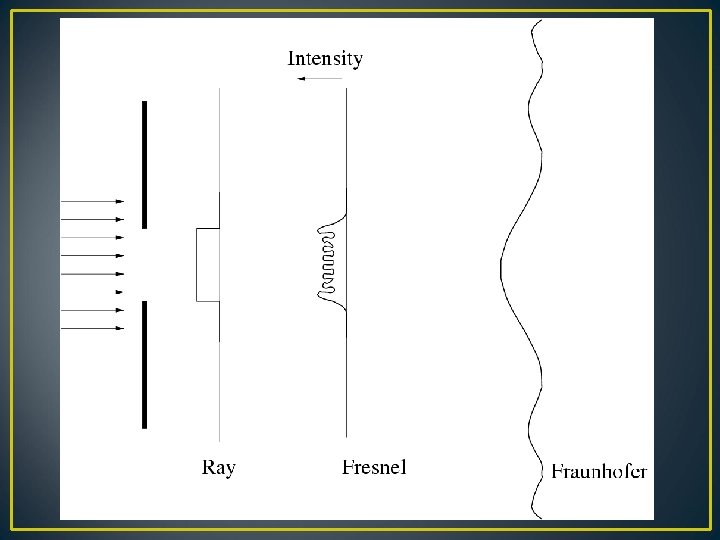
Diffraction ``Any deviation of light rays from rectilinear path which is neither reflection nor refraction known as diffraction. ’’ (Sommerfeld) Types or kinds of diffraction: 1. Fraunhofer (1787 -1826) 2. Fresnel (1788 -1827)

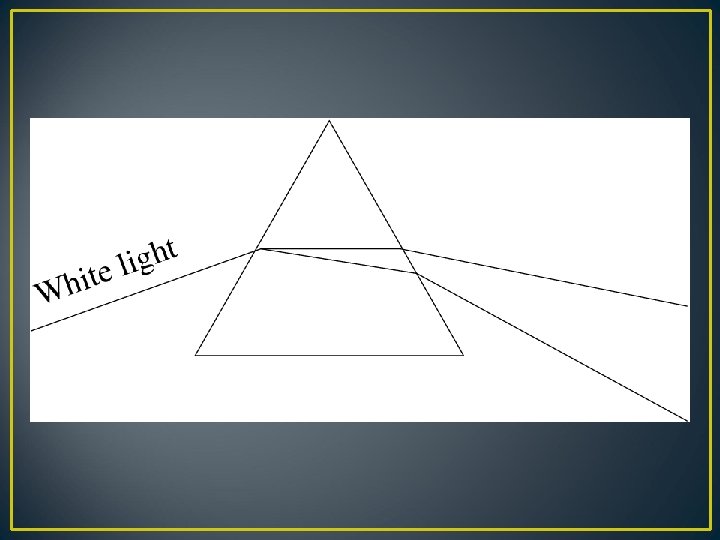
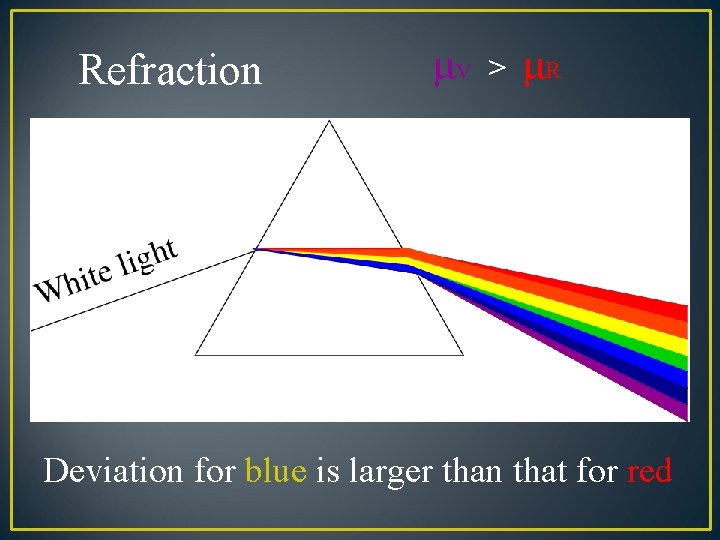
Refraction μv > μR Deviation for blue is larger than that for red

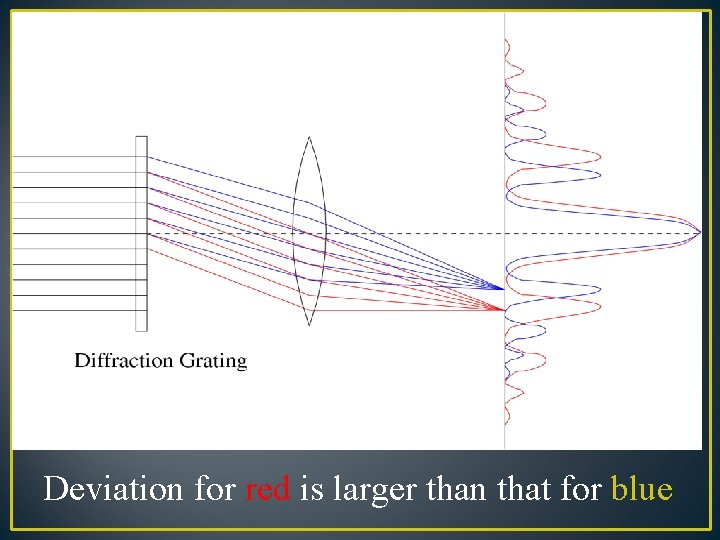
Diffraction Deviation for red is larger than that for blue

Secondary wavelets from apertures

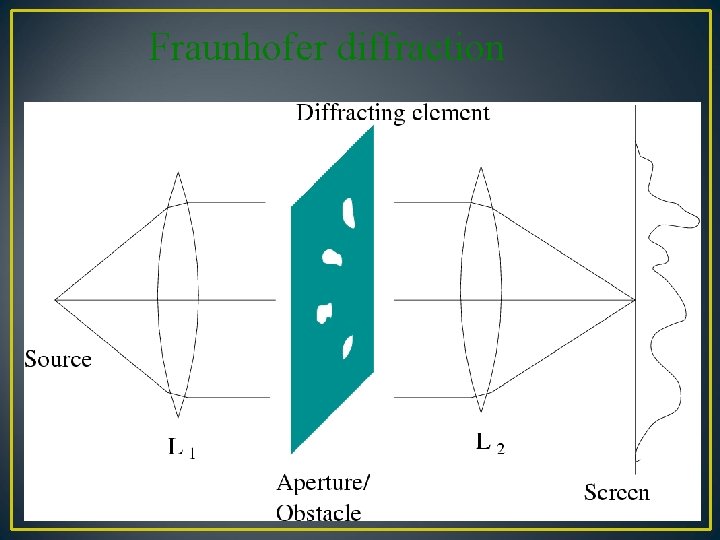
Fraunhofer diffraction

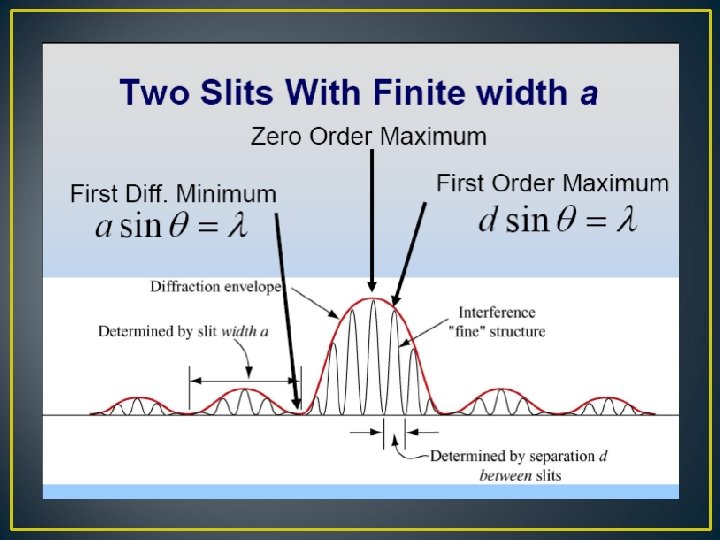
Single slit diffraction Principal maximum

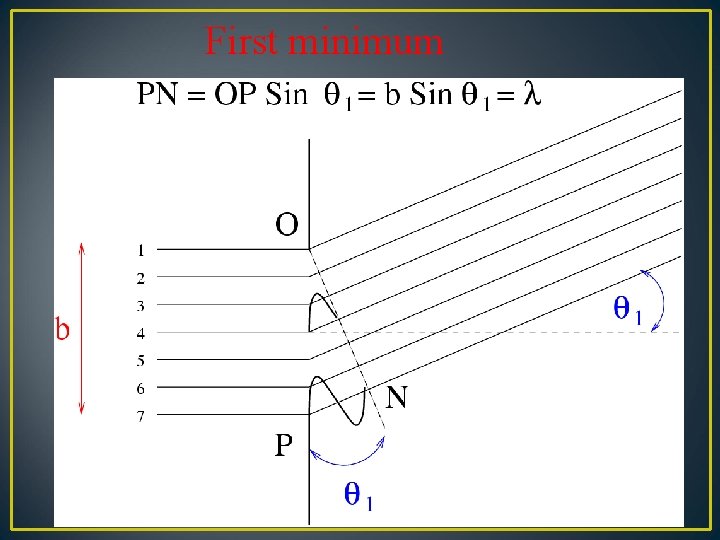
First minimum

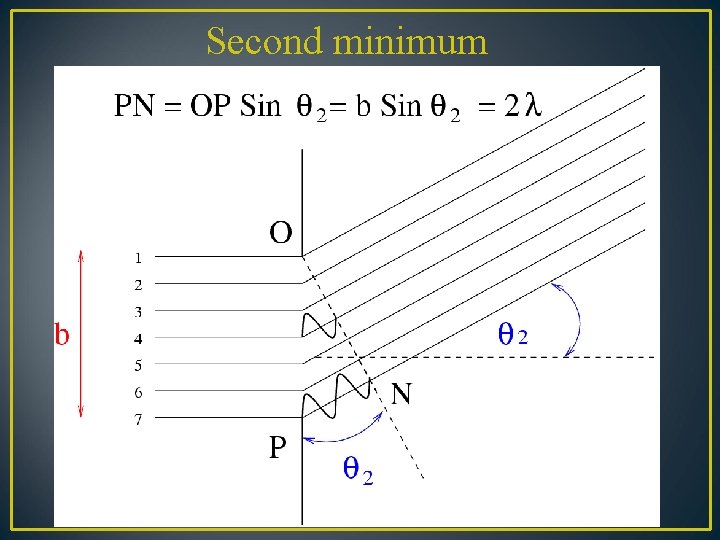
Second minimum

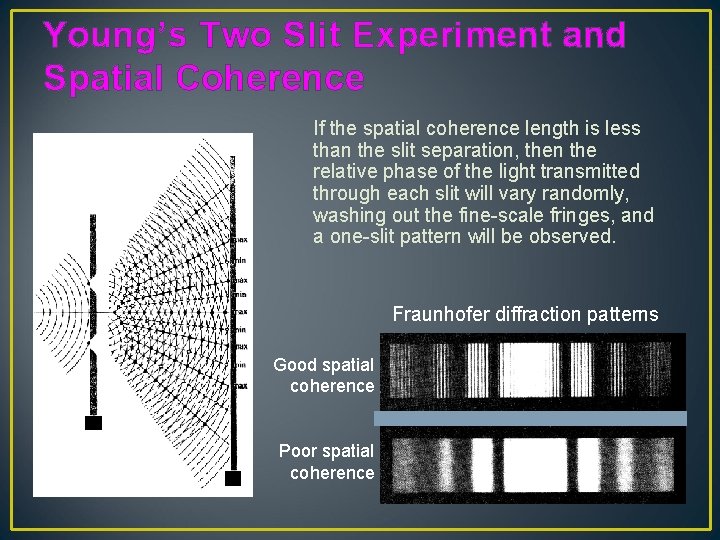
Young’s Two Slit Experiment and Spatial Coherence If the spatial coherence length is less than the slit separation, then the relative phase of the light transmitted through each slit will vary randomly, washing out the fine-scale fringes, and a one-slit pattern will be observed. Fraunhofer diffraction patterns Good spatial coherence Poor spatial coherence

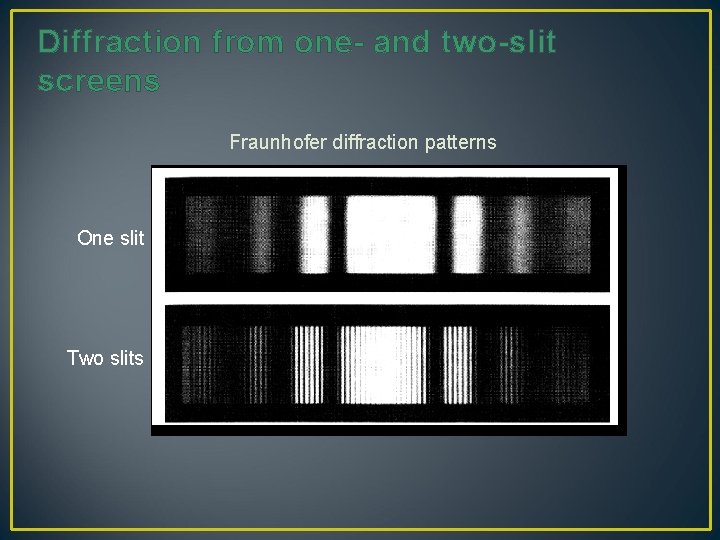
Diffraction from one- and two-slit screens Fraunhofer diffraction patterns One slit Two slits

Diffraction from small and large circular apertures Far-field intensity pattern from a small aperture Far-field intensity pattern from a large aperture

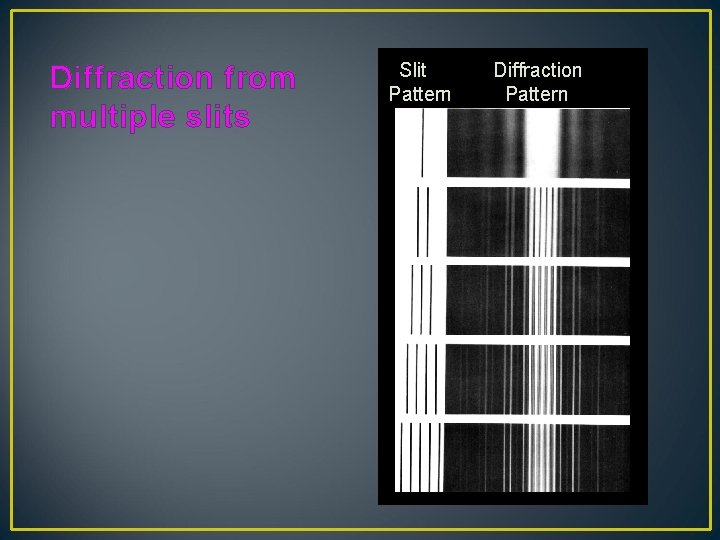
Diffraction from multiple slits Slit Pattern Diffraction Pattern

Superposition of large number of phasors of equal amplitude a and equal successive phase difference δ. Find the resultant phasor.

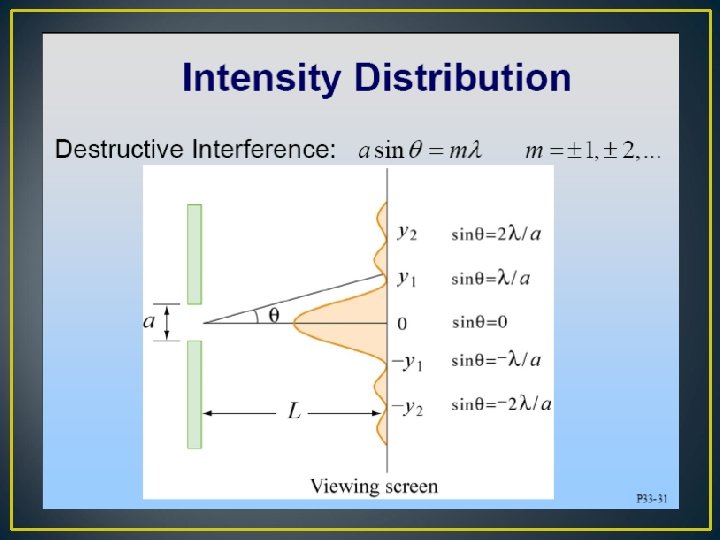
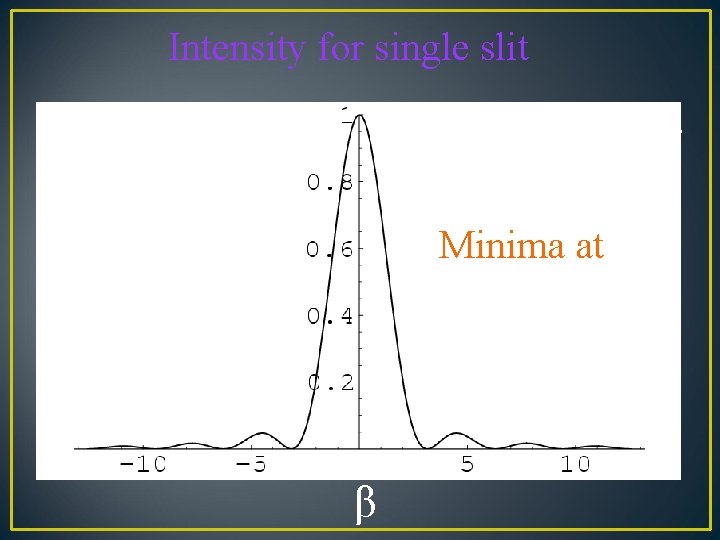
For single slit path difference between the two ends of the slit Δ = a Sin θ Phase difference = 2 π Δ / λ = n δ β = n δ / 2 = π a Sin θ / λ

Intensity for single slit β = π a Sin θ / λ I Minima at β = +_ m π β