ENGINEERING OPTIMIZATION Methods and Applications A Ravindran K

ENGINEERING OPTIMIZATION Methods and Applications A. Ravindran, K. M. Ragsdell, G. V. Reklaitis Book Review Page 1

Chapter 5: Constrained Optimality Criteria Part 1: Ferhat Dikbiyik Part 2: Yi Zhang Review Session July 2, 2010 Page 2

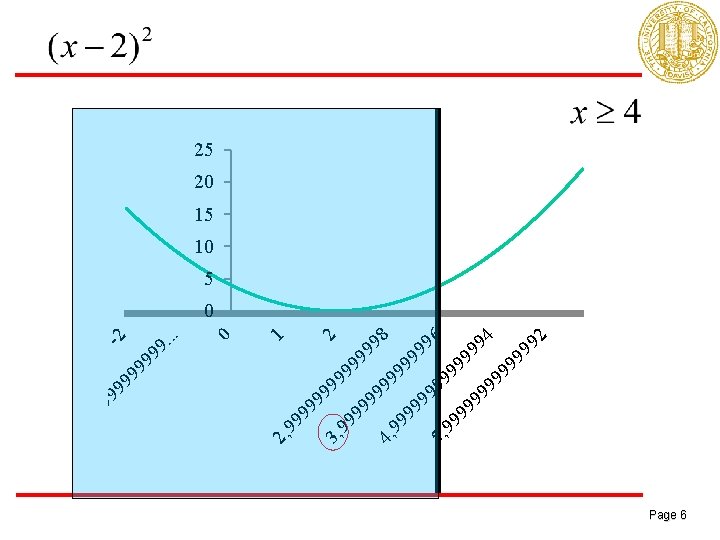
Constraints: Good guys or bad guys? Page 3

Constraints: Good guys or bad guys? reduces the region in which we search for optimum. Page 4

Constraints: Good guys or bad guys? makes optimization process very complicated Page 5

4 92 99 99 99 6 99 99 99 5, 2 1 0 8 99 9 99 4, 99 9 99 3, 99 9 99 2, -2 9. . . 99 99 99 , 9 -0 25 20 15 10 5 0 Page 6

Outline of Part 1 • Equality-Constrained Problems • Lagrange Multipliers • Economic Interpretation of Lagrange Multipliers • Kuhn-Tucker Conditions • Kuhn-Tucker Theorem Page 7

Outline of Part 1 • Equality-Constrained Problems • Lagrange Multipliers • Economic Interpretation of Lagrange Multipliers • Kuhn-Tucker Conditions • Kuhn-Tucker Theorem Page 8

Equality-Constrained Problems GOAL solving the problem as an unconstrained problem by explicitly eliminating K independent variables using the equality constraints Page 9

Example 5. 1 Page 10

What if? Page 11

Outline of Part 1 • Equality-Constrained Problems • Lagrange Multipliers • Economic Interpretation of Lagrange Multipliers • Kuhn-Tucker Conditions • Kuhn-Tucker Theorem Page 12

Lagrange Multipliers Converting constrained problem to an unconstrained problem with help of certain unspecified parameters known as Lagrange Multipliers Page 13

Lagrange Multipliers Lagrange function Page 14

Lagrange Multipliers Lagrange multiplier Page 15

Example 5. 2 Page 16

Page 17

Test whether the stationary point corresponds to a minimum positive definite Page 18

Page 19

Example 5. 3 Page 20

Page 21

Page 22

max positive definite negative definite Page 23

Outline of Part 1 • Equality-Constrained Problems • Lagrange Multipliers • Economic Interpretation of Lagrange Multipliers • Kuhn-Tucker Conditions • Kuhn-Tucker Theorem Page 24

Economic Interpretation of Lagrange Multipliers The Lagrange multipliers have an important economic interpretation as shadow prices of the constraints, and their optimal values are very useful in sensitivity analysis. Page 25

Outline of Part 1 • Equality-Constrained Problems • Lagrange Multipliers • Economic Interpretation of Lagrange Multipliers • Kuhn-Tucker Conditions • Kuhn-Tucker Theorem Page 26

Kuhn-Tucker Conditions Page 27

NLP problem Page 28

Kuhn-Tucker conditions (aka Kuhn-Tucker Problem) Page 29

Example 5. 4 Page 30

Example 5. 4 Page 31

Example 5. 4 Page 32

Outline of Part 1 • Equality-Constrained Problems • Lagrange Multipliers • Economic Interpretation of Lagrange Multipliers • Kuhn-Tucker Conditions • Kuhn-Tucker Theorem Page 33

Kuhn-Tucker Theorems 1. Kuhn – Tucker Necessity Theorem 2. Kuhn – Tucker Sufficient Theorem Page 34

Kuhn-Tucker Necessity Theorem Let • f, g, and h be differentiable functions • x* be a feasible solution to the NLP problem. • • and for k=1, …. , K are linearly independent Page 35

Kuhn-Tucker Necessity Theorem Let f, g, and. Constraint h be differentiable functions x* be a qualification feasible solution to the NLP problem. • and for k=1, …. , K are linearly independent at the optimum If x* is an optimal solution NLP problem, ! Hard to verify, sincetoitthe requires that then there exists a (u*, v*) suchbe thatknown (x*, u*, v*) the optimum solution solves the KTP given by KTC. ! beforehand Page 36

Kuhn-Tucker Necessity Theorem For certain special NLP problems, the constraint qualification is satisfied: 1. When all the inequality and equality constraints are linear 2. When all the inequality constraints are concave functions and equality constraints are linear ! When the constraint qualification is not met at the optimum, there may not exist a solution to the KTP Page 37

Example 5. 5 x* = (1, 0) and for k=1, …. , K are linearly independent at the optimum Page 38

Example 5. 5 x* = (1, 0) No Kuhn-Tucker point at the optimum Page 39

Kuhn-Tucker Necessity Theorem Given a feasible point that satisfies the constraint qualification optimal not optimal If it does not satisfy the KTCs If it does satisfy the KTCs Page 40

Example 5. 6 Page 41

Kuhn-Tucker Sufficiency Theorem Let • f(x) be convex • the inequality constraints gj(x) for j=1, …, J be all concave function • the equality constraints hk(x) for k=1, …, K be linear If there exists a solution (x*, u*, v*) that satisfies KTCs, then x* is an optimal solution Page 42

Example 5. 4 • f(x) be convex • the inequality constraints gj(x) for j=1, …, J be all concave function • the equality constraints hk(x) for k=1, …, K be linear Page 43

Example 5. 4 • f(x) be convex semi-definite Page 44

Example 5. 4 • f(x) be convex v • the inequality constraints gj(x) for j=1, …, J be all concave function g 1(x) linear, hence both convex and concave negative definite Page 45

Example 5. 4 • f(x) be convex v • the inequality constraints gj(x) for j=1, …, J be all concave function • the equality constraints hk(x) for k=1, …, K be linear Page 46

Remarks For practical problems, the constraint qualification will generally hold. If the functions are differentiable, a Kuhn–Tucker point is a possible candidate for the optimum. Hence, many of the NLP methods attempt to converge to a Kuhn– Tucker point. Page 47

Remarks When the sufficiency conditions of Theorem 5. 2 hold, a Kuhn–Tucker point automatically becomes the global minimum. Unfortunately, the sufficiency conditions are difficult to verify, and often practical problems may not possess these nice properties. Note that the presence of one nonlinear equality constraint is enough to violate the assumptions of Theorem 5. 2 Page 48

Remarks The sufficiency conditions of Theorem 5. 2 have been generalized further to nonconvex inequality constraints, nonconvex objectives, and nonlinear equality constraints. These use generalizations of convex functions such as quasi-convex and pseudoconvex functions Page 49