Engineering Mechanics Statics Mustansiriyah University 15 Mechanical Engineering

Engineering Mechanics (Statics) Mustansiriyah University (15) Mechanical Engineering Dep. Faculty of Engineering Lecturer: Dr. Muhanad Nazar Centroids and Centers of Gravity The Center of Gravity of a Body To determine mathematically the position of the center of gravity of any body, Figure 1, we apply the principle of moments to the parallel system of gravitational forces. The moment of the resultant gravitational force W about any axis equals the sum of the moments about the same axis of the gravitational forces. The resultant considering number weight the of of plate small the to plate be elements can made each be up having determined of a an weight by infinite given by the expression: ���� = �� �� ���� Figure 1 Where d. W is the weight of an element, γ is the specific weight of the material (weight per unit volume), t is the thickness of the plate, and d. A is the area of the element (surface area in xy plane). The total weight of the plate is: �� = ∫ ���� The coordinates of a point on the line of action of the resultant weight can be determined by the principle of moments. The moment of the weight of the element about the x axis is ���� = �� ���� and �� �� = ∫ �� ���� �� The y coordinate of a point on the action line of the resultant is �� �� ∫ ����� = -----------------(1) �� ∫ ���� In a similar manner, the x coordinate of a point on the action line of the resultant is found to be �� = ∫ ����� -----------------(2) ∫ ���� 1

The center of gravity of the body is on a line parallel to the z axis through the point (�� ) . When t and γ are constant, �� , �� can be obtained by symmetry. If either t or γ is a variable, the plate can be rotated so that either the x axis or the y axis is vertical. Then the principle of moments gives �� = ∫ ���� Where d. V is equal to d. A dt ∫ ������ Centroids If the plate in Figure 1 has a constant thickness and is homogeneous (has a constant specific weight), the product t γ in Equations (1) and (2) can be taken outside the integral signs and eliminated from the equations, leaving � ���� ∫ ����� � =� = ∫ �� , �� ∫ ���� In each of these equations, the denominator is the surface area of the plate in the xy plane, and the numerator is called the first moment of the area with respect to the x or the y axis. Note: The term “first moment” is used to distinguish this quantity from the second moment, or moment of inertia. The point located by the coordinates �� and � is�defined as the centroid of the area of the top surface of the plate. Since an area has no thickness, the centroid must lie in the plane of the area, and two coordinates are sufficient to locate it. 2

Centroids and Centers of Gravity by Integration Sometimes it is possible to determine or both of the coordinates of the centroid from symmetry, as for example the coordinates of the centroid of a rectangular or a circular area. The location of the centroid of an area by integration involves the selection and use of an element of that area. The element can usually be selected in such a manner that only one integration is necessary. Sometimes, however, it may be necessary to use double integration or perhaps triple integration for volumes. The element must be selected in such a manner that the distance from its centroid to the moment axis or plane is known. The following examples illustrate the use of different types of elements and the sequence of steps used to locate the centroid of a figure or the center of gravity or mass of a body. Example 1. Determine the coordinates of the centroid of the circular arc (line) in Figure 2. Solution. From symmetry, the centroid must lie on a line through the origin at an angle α/2 with the x axis; therefore it is necessary to integrate for only one coordinate of the centroid since the other can be found by trigonometry. Figure 2 The length of the element is ���� = ������ The length of the arc, determined by integrating the length of the element, is ∝ ]�� �� = ∫ 0 �� ���� = [���� = 0 ���� The angle α is expressed in radians, and the length L could have been obtained directly from the definition of a radian. The moment of the element with respect to the y axis is 2(���� )(������ ) = �� )���� = �� ���� = (����� �� The moment of the arc with respect to the y axis as determined by integrating the moment of the element is ∝ 2(�������� 2 ���� ]�� �� = ∫ 0�� ) ���� = [�� =0 �� �� The x coordinate of the centroid of the arc is determined by dividing the moment of the arc with respect to the y axis by the length of the arc; thus 3

2 �� ∝ ������ ∝ � =��� t an ( ∝ ) = ������ ∝ ∝ �� = ���� and �� �� ∝ ∝ 2 2 ∝ When the angle ∝ is 90° or �� /2 radians, the x coordinate of the centroid is the same as the y coordinate (by symmetry) and is 2�� �� =� =� �� Example 2. Determine the coordinates of the centroid of the area in Figure 3 bounded by the curve y = x 2 and the line y = x+2. In the equation x and y are in inches. Solution. A vertical element of area is selected because the same element can be used for the entire area. If a horizontal element were chosen, it would be necessary to use two different elements. Note that the element is completely dimensioned. The area of the element is: 2 ) ���� = (�� + 2 − �� 1)���� And the total area is 2 �� 3 2 2 2 ) ���� (+ 2 − �� = [ + 2�� − �� ] = �� = ∫− 1�� 2 Figure 3 3 − 1 4. 5 ���� The moment of the element with respect to the y axis is 2 ) ���� 2 + 2�� 3 ) ���� (�� ���� = �� + 2 − �� = ( �� − �� �� And the total moment is 3 4 2 �� 2 3) 2 − �� 3 ( 2 + 2�� �� − �� ���� = [ 3 + �� ] = 2. 25 ���� �= � ∫− 1 �� 4 − 1 The x coordinate of the centroid is �� 2. 25 �� = �� 0. 5 ���� 4. 5 The positive result indicates that the centroid is to the right of the y axis. The element used above is parallel to the y axis and thus was selected in accordance with the first rule for selecting the element when determining the moment with respect to the y axis. If the same element is used to determine the moment about the x axis, the location of the centroid of the element must be obtained with respect to the x axis. Since the element is a rectangle, the centroid is at the midpoint, which is a distance Above the x axis, and the first moment of the element with respect to the x axis is 4

The moment of the entire area with respect to the x axis is The y coordinate of the centroid is �� = ���� = 7. 2 �� 4. 5 = 1. 6 ���� The centroid of the area is 0. 5 in to the right of the y axis and 1. 6 in above the x axis. Example 3. Locate the centroid of the semicircular area in Figure 4. Solution. By symmetry, the centroid must be on the y axis; therefore it is necessary only to determine ��. The element of area is approximately a rectangle of length ���� and width ������ , and the area of the element is ���� = ����� Figure 4 It is not necessary to integrate this expression for the area, since the area of a semicircle is 2 ���� �� = 2 The centroidal distance from the x axis to the element is �� = �� ���� and the moment of the element with respect to the x axis is ���� = ������ = (���������� ) �� The moment of the entire area about the x axis is �� =∫ �� �� 3 �� �� 2 ∫ �� ���� = ∫ [ ] ���� = [ (−���� )] = 0 0 0 3 0 3 From the principle of moments, the y coordinate of the centroid is �� �� � =� = 4�� �� 3�� 5

Example 4. Determine the coordinates of the center of mass of the frustum of a homogeneous right circular cone shown in Figure 5. Solution. By symmetry, �� and � � are both zero. In order to determine the z coordinate of the mass center, the moment of the mass of the frustum of the cone with respect to the xy plane is needed. A thin, circular disk of radius x and thickness dz is selected as the element of mass because all parts of it are the same distance from the xy plane. The mass of this element is Dm =ρ d. V = ρπx 2 dz Figure 5 Where ρ is the density (mass per unit volume) of the material of the body and d. V is the volume of the element. The relationship between x and z may be obtained from similar triangles as �� 6 = 4−� � 4− 1 from which �� =4− �� 2 The mass of the element then become � 2� 4 ���� = ���� (16 − 4�� + ) ���� And the total mass of the body is 2 6 �� = ���� + �� = 42 ���� ) ���� ∫ 0(16 − 4�� 4 The moment of the mass of the element with respect to the xy plane is � 3� 4 2+ ���� = ���� (16�� − 4�� ) ���� � �= ������ �� and the moment of the body is 3 6 2 + �� ��= − 4�� = 81 ���� ) ���� ∫ 0(16�� � � ���� 4 �� From the principle of moments, the z coordinate of the mass center is �� �� = ���� = 81 ���� = 1. 929 ���� �� 42 ���� Above the xy plane. If the material in the body had not been homogeneous, the density, ρ, would have been a variable and could not have been taken outside the integral sign. In this case the problem could not be solved without first obtaining the law relating the density and the coordinates of any point in the body. 6

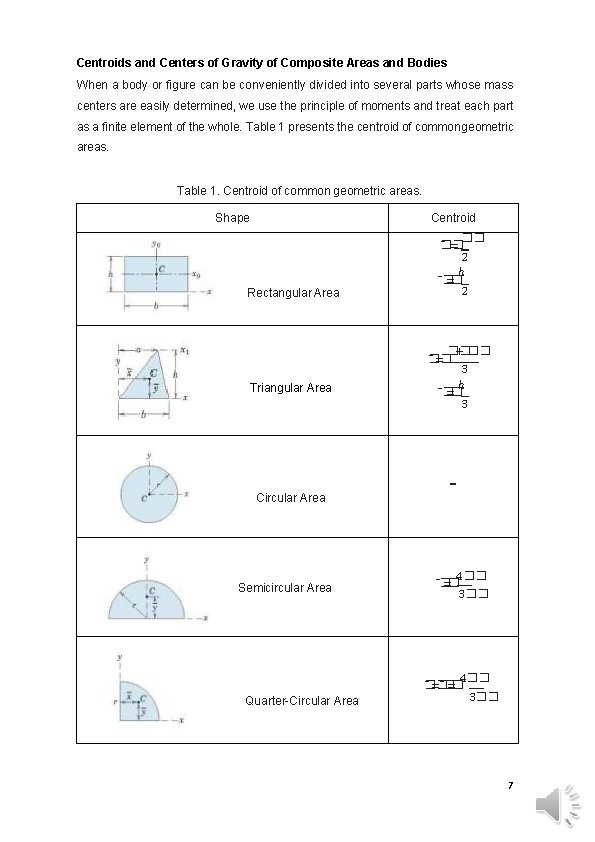
Centroids and Centers of Gravity of Composite Areas and Bodies When a body or figure can be conveniently divided into several parts whose mass centers are easily determined, we use the principle of moments and treat each part as a finite element of the whole. Table 1 presents the centroid of common geometric areas. Table 1. Centroid of common geometric areas. Shape Centroid Rectangular Area Triangular Area Circular Area Semicircular Area Quarter-Circular Area �� �� = 2 ℎ � =� 2 �� + �� �� = 3 ℎ � =� 3 - 4�� � =� 3�� 4�� �� =� 3�� 7

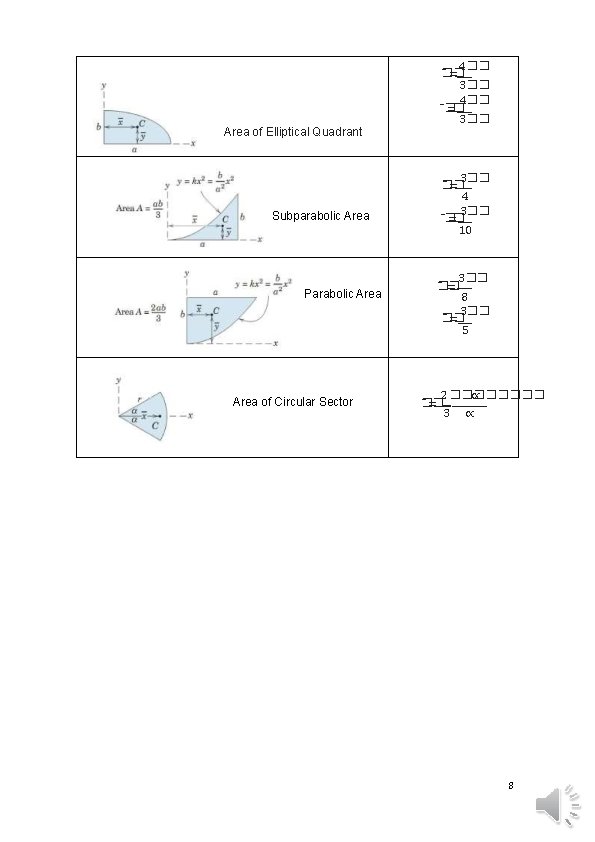
Area of Elliptical Quadrant Subparabolic Area Parabolic Area of Circular Sector 4�� �� = 3�� 4�� � =� 3�� �� = 4 3�� � =� 10 3�� �� = 8 3�� �� = 5 2 ���� ∝ �� = 3 ∝ 8

Example 1. Determine the coordinates of the centroid of the shaded area in the figure below. Solution 1. The composite area is divided into two right triangles A and B, a large rectangle C, and a small rectangle D whose area is to be removed. All necessary data for each area are arranged in a compact and convenient form in the following table. Symbol used in sketch Area (in 2) A B C D Total 27 9 48 -12 72 X coordinate of centroid (in) 3 7 3 4. 5 My (in 3) y coordinate of centroid (in) 81 63 144 -54 234 2 2 -2 -1 Mx (in 3) 54 18 -96 12 -12 The coordinates of the centroid can be obtained by applying the principle of moments for areas. They are �� 234 �� = �� = = 3. 25 ���� �� 72 and �� �� − 12 � =� = = − 0. 1667 ���� below the x �� axis 72 9

Example 2. The composite body in the figure consists of the 322 - lb homogeneous cylindrical disk A, the 257. 6 -lb homogeneous slender rod BC, and the 64. 4 -lb homogeneous slender rod CD. The xy plane of symmetry, and the diameters of the rods may be neglected. Determine the coordinates of the center of mass of the composite body. Solution. The z coordinate of the mass center of the body is zero, by symmetry. The mass of a body can be determined by dividing its weight by the acceleration of gravity, that is, the acceleration the weight would produce if it were the only force acting on the body Thus the total mass of the composite body is. 2 ������ �� = 322 + 257. 6 + 64. 4 = 20 ���� − ������ = 20 ����� 32. 2 The moment of the mass of the body with respect to the yz plane is �� = 10(− 5) + 8(2) + 2(7) = − 20 ���� − ���� and the x coordinate of the centroid is �� �� = ���� = − 20 = − 1 ���� to the left of the yz plane �� 20 Similarly, the moment of the mass with respect to the xz plane is �� = 10(0) + 8(0) + 2(2) = 4 slug-ft ���� And the y coordinate of the centroid is ���� � =��� = �� 4 20 = 0. 2 ���� 10

Example 3. Locate the centroid of the shaded area. Solution. The composite area is divided into the four elementary shapes shown in the lower figure. The centroid locations of all these shapes may be obtained from the table below. Note that the areas of the “holes” (parts 3 and 4) are taken as negative in the following table. 11