Engineering Mechanics Statics in SI Units 12 e

Engineering Mechanics: Statics in SI Units, 12 e 4 Force System Resultants Copyright © 2010 Pearson Education South Asia Pte Ltd

Chapter Objectives • Concept of moment of a force in two and three dimensions • Method for finding the moment of a force about a specified axis. • Define the moment of a couple. • Determine the resultants of non-concurrent force systems • Reduce a simple distributed loading to a resultant force having a specified location Copyright © 2010 Pearson Education South Asia Pte Ltd

Chapter Outline 1. 2. 3. 4. 5. 6. 7. 8. 9. Moment of a Force – Scalar Formation Cross Product Moment of Force – Vector Formulation Principle of Moments Moment of a Force about a Specified Axis Moment of a Couple Simplification of a Force and Couple System Further Simplification of a Force and Couple System Reduction of a Simple Distributed Loading Copyright © 2010 Pearson Education South Asia Pte Ltd

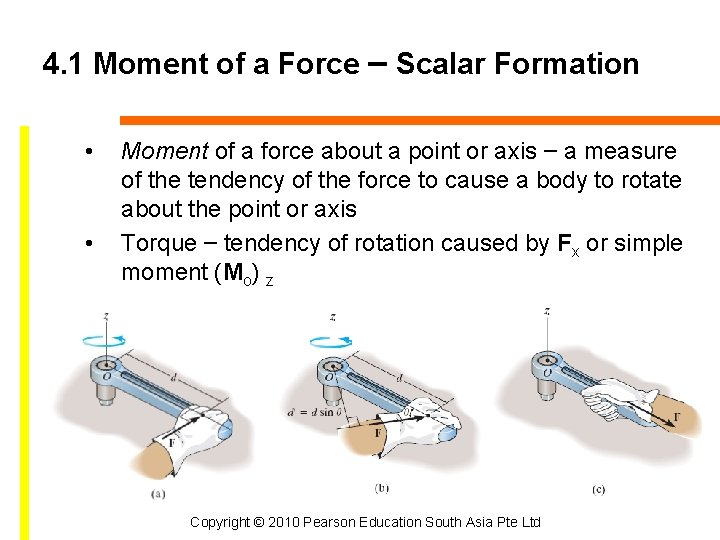
4. 1 Moment of a Force – Scalar Formation • • Moment of a force about a point or axis – a measure of the tendency of the force to cause a body to rotate about the point or axis Torque – tendency of rotation caused by Fx or simple moment (Mo) z Copyright © 2010 Pearson Education South Asia Pte Ltd

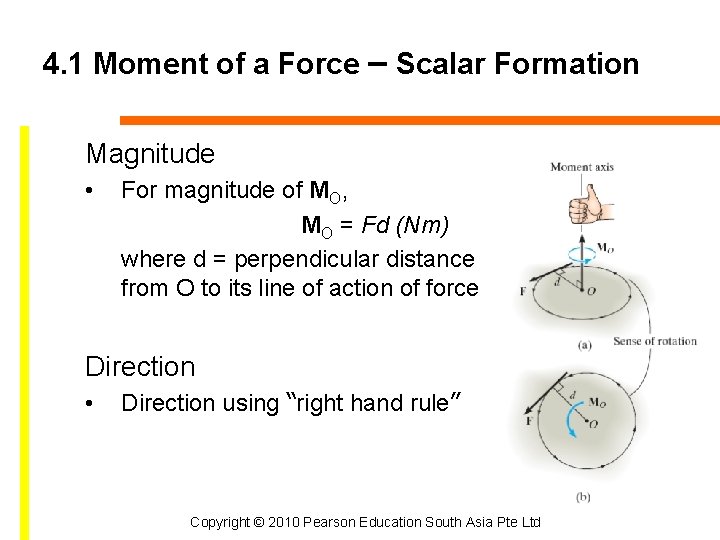
4. 1 Moment of a Force – Scalar Formation Magnitude • For magnitude of MO, MO = Fd (Nm) where d = perpendicular distance from O to its line of action of force Direction • Direction using “right hand rule” Copyright © 2010 Pearson Education South Asia Pte Ltd

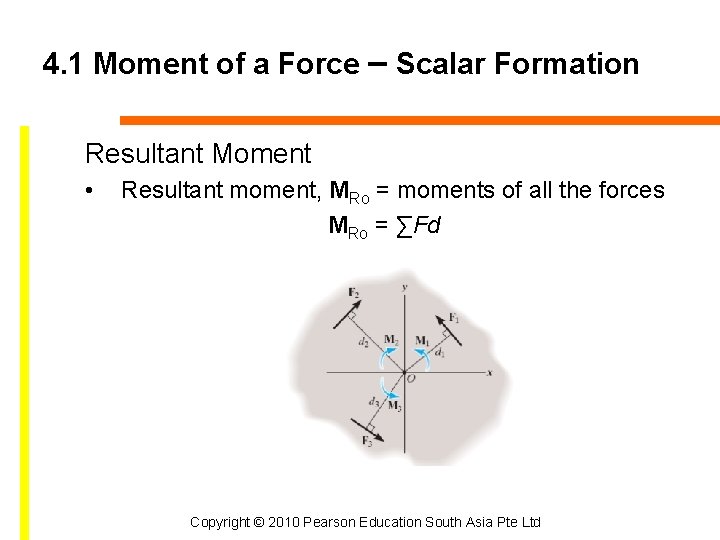
4. 1 Moment of a Force – Scalar Formation Resultant Moment • Resultant moment, MRo = moments of all the forces MRo = ∑Fd Copyright © 2010 Pearson Education South Asia Pte Ltd

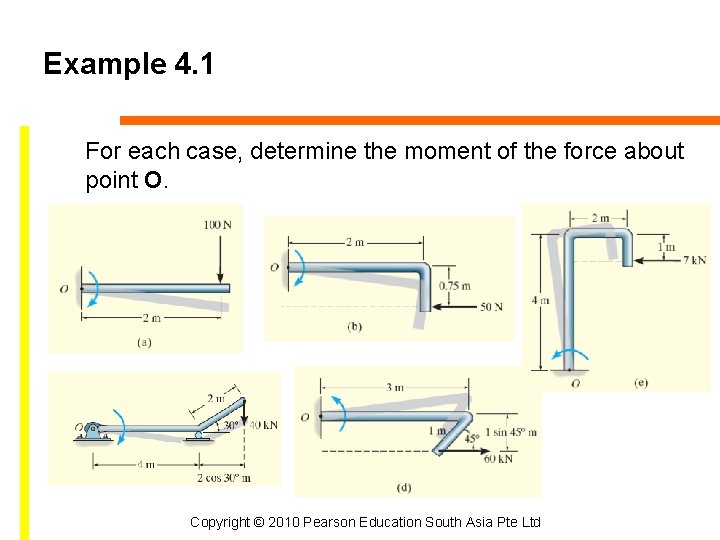
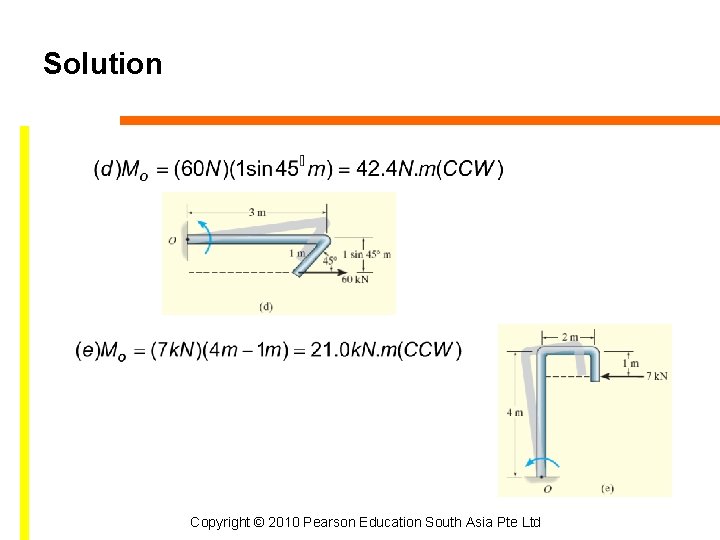
Example 4. 1 For each case, determine the moment of the force about point O. Copyright © 2010 Pearson Education South Asia Pte Ltd

Solution Line of action is extended as a dashed line to establish moment arm d. Tendency to rotate is indicated and the orbit is shown as a colored curl. Copyright © 2010 Pearson Education South Asia Pte Ltd

Solution Copyright © 2010 Pearson Education South Asia Pte Ltd

Solution Copyright © 2010 Pearson Education South Asia Pte Ltd

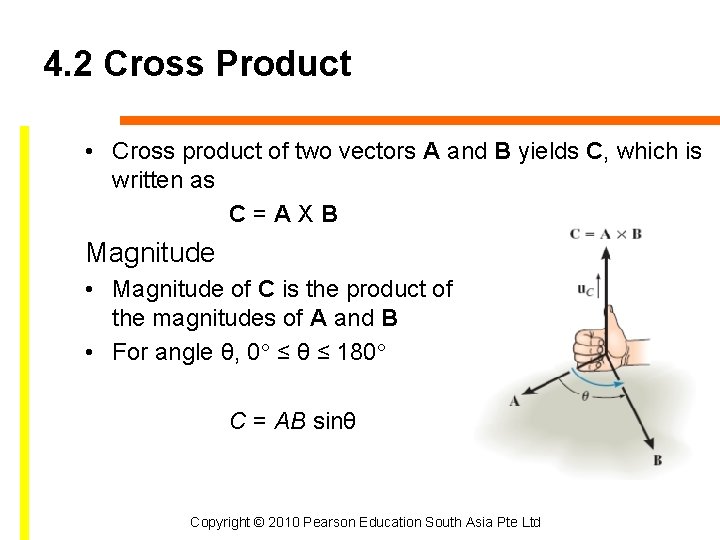
4. 2 Cross Product • Cross product of two vectors A and B yields C, which is written as C=AXB Magnitude • Magnitude of C is the product of the magnitudes of A and B • For angle θ, 0° ≤ θ ≤ 180° C = AB sinθ Copyright © 2010 Pearson Education South Asia Pte Ltd

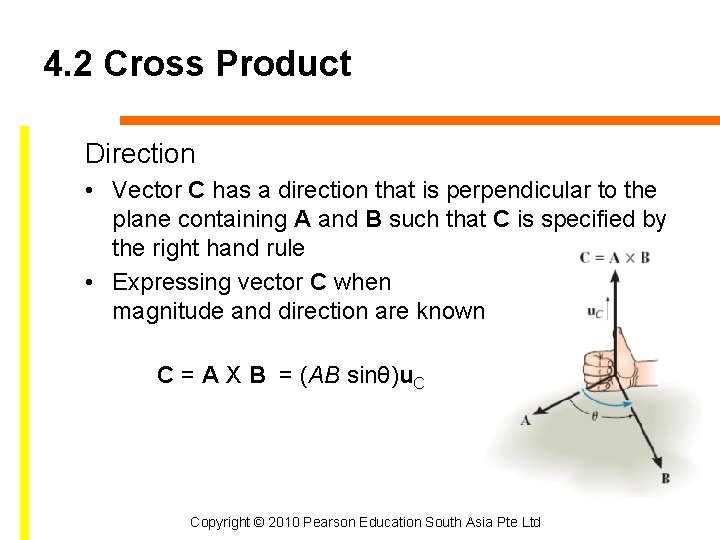
4. 2 Cross Product Direction • Vector C has a direction that is perpendicular to the plane containing A and B such that C is specified by the right hand rule • Expressing vector C when magnitude and direction are known C = A X B = (AB sinθ)u. C Copyright © 2010 Pearson Education South Asia Pte Ltd

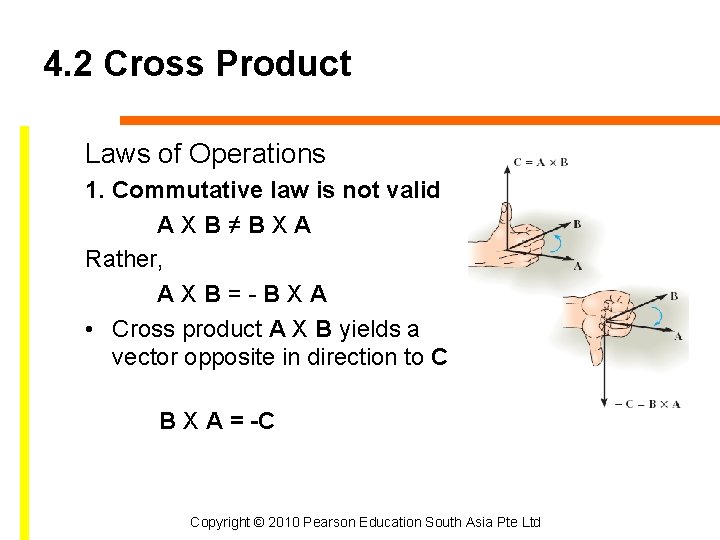
4. 2 Cross Product Laws of Operations 1. Commutative law is not valid AXB≠BXA Rather, AXB=-BXA • Cross product A X B yields a vector opposite in direction to C B X A = -C Copyright © 2010 Pearson Education South Asia Pte Ltd

4. 2 Cross Product Laws of Operations 2. Multiplication by a Scalar a( A X B ) = (a. A) X B = A X (a. B) = ( A X B )a 3. Distributive Law AX(B+D)=(AXB)+(AXD) • Proper order of the cross product must be maintained since they are not commutative Copyright © 2010 Pearson Education South Asia Pte Ltd

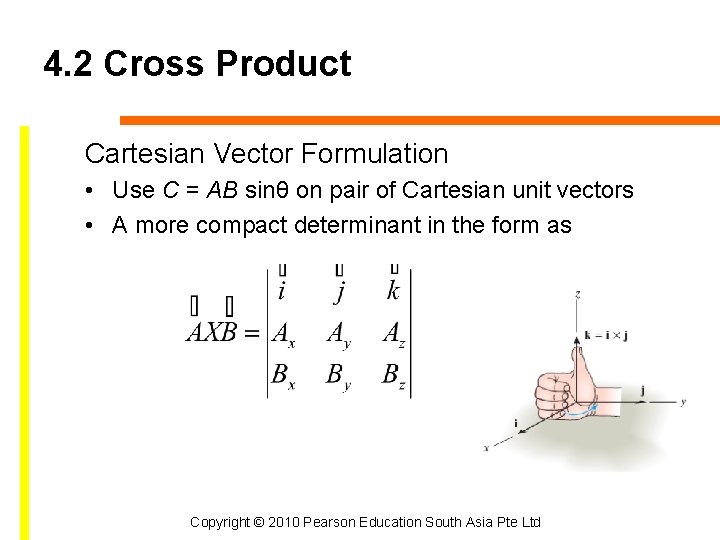
4. 2 Cross Product Cartesian Vector Formulation • Use C = AB sinθ on pair of Cartesian unit vectors • A more compact determinant in the form as Copyright © 2010 Pearson Education South Asia Pte Ltd

4. 3 Moment of Force - Vector Formulation • Moment of force F about point O can be expressed using cross product MO = r X F Magnitude • For magnitude of cross product, MO = r. F sinθ • Treat r as a sliding vector. Since d = r sinθ, MO = r. F sinθ = F (rsinθ) = Fd Copyright © 2010 Pearson Education South Asia Pte Ltd

4. 3 Moment of Force - Vector Formulation Direction • Direction and sense of MO are determined by righthand rule *Note: - “curl” of the fingers indicates the sense of rotation - Maintain proper order of r and F since cross product is not commutative Copyright © 2010 Pearson Education South Asia Pte Ltd

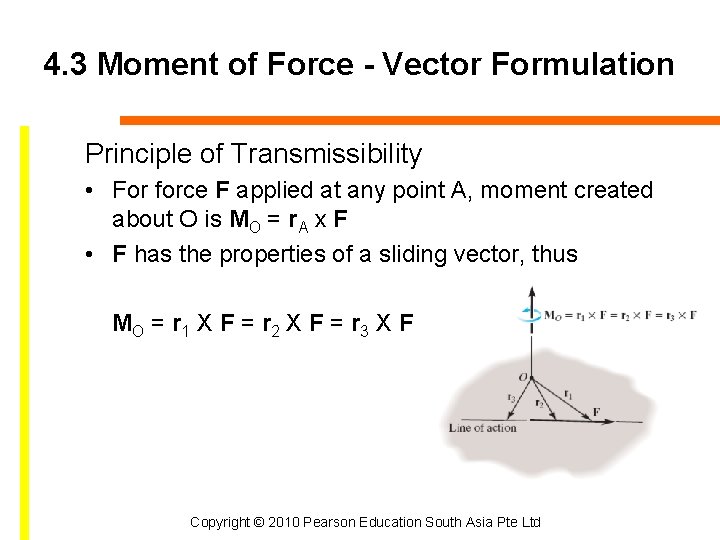
4. 3 Moment of Force - Vector Formulation Principle of Transmissibility • For force F applied at any point A, moment created about O is MO = r. A x F • F has the properties of a sliding vector, thus MO = r 1 X F = r 2 X F = r 3 X F Copyright © 2010 Pearson Education South Asia Pte Ltd

4. 3 Moment of Force - Vector Formulation Cartesian Vector Formulation • For force expressed in Cartesian form, • With the determinant expended, MO = (ry. Fz – rz. Fy)i – (rx. Fz - rz. Fx)j + (rx. Fy – y. Fx)k Copyright © 2010 Pearson Education South Asia Pte Ltd

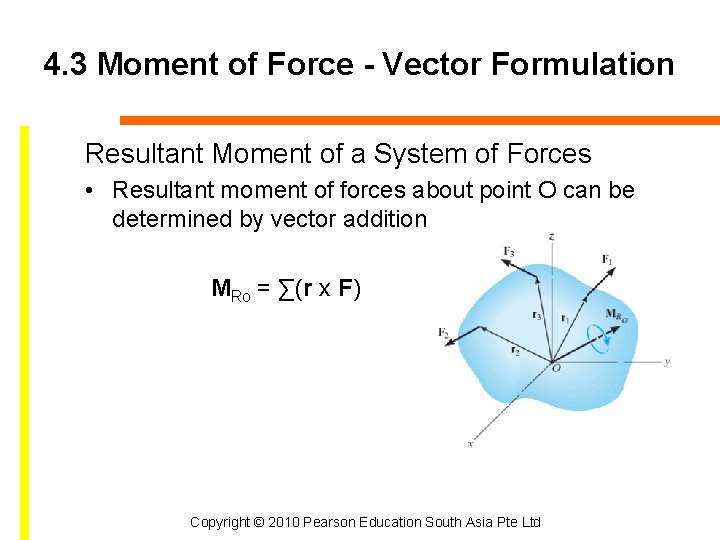
4. 3 Moment of Force - Vector Formulation Resultant Moment of a System of Forces • Resultant moment of forces about point O can be determined by vector addition MRo = ∑(r x F) Copyright © 2010 Pearson Education South Asia Pte Ltd

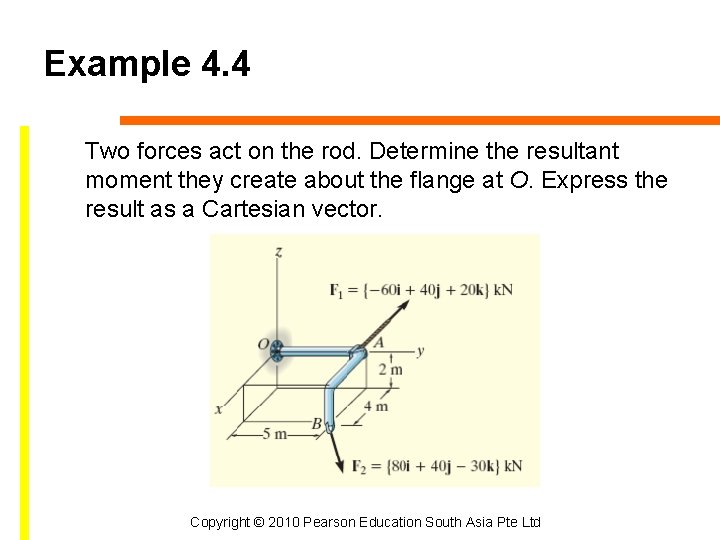
Example 4. 4 Two forces act on the rod. Determine the resultant moment they create about the flange at O. Express the result as a Cartesian vector. Copyright © 2010 Pearson Education South Asia Pte Ltd

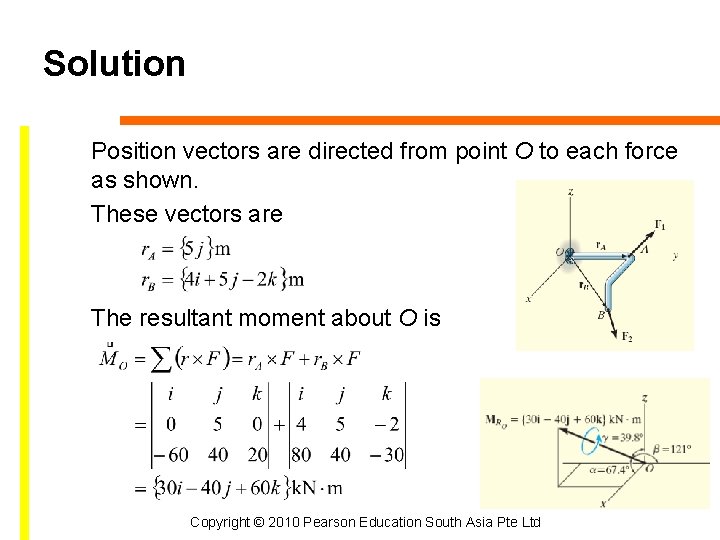
Solution Position vectors are directed from point O to each force as shown. These vectors are The resultant moment about O is Copyright © 2010 Pearson Education South Asia Pte Ltd

4. 4 Principles of Moments • Also known as Varignon’s Theorem “Moment of a force about a point is equal to the sum of the moments of the forces’ components about the point” • Since F = F 1 + F 2, MO = r X F = r X (F 1 + F 2) = r X F 1 + r X F 2 Copyright © 2010 Pearson Education South Asia Pte Ltd

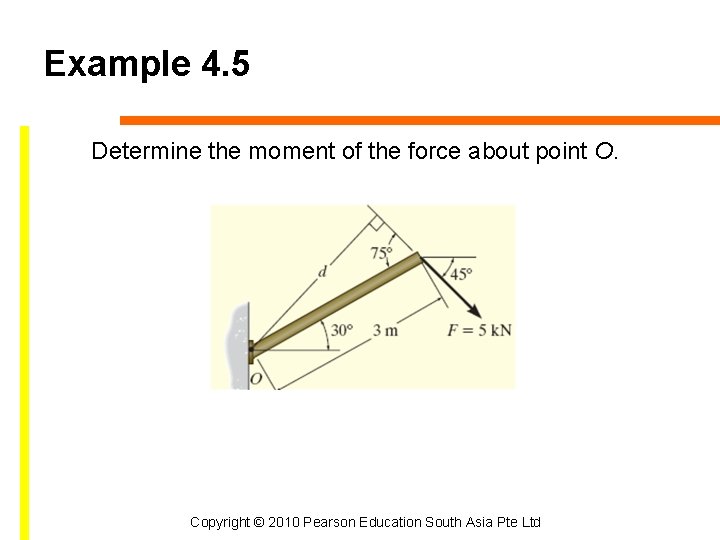
Example 4. 5 Determine the moment of the force about point O. Copyright © 2010 Pearson Education South Asia Pte Ltd

Solution The moment arm d can be found from trigonometry, Thus, Since the force tends to rotate or orbit clockwise about point O, the moment is directed into the page. Copyright © 2010 Pearson Education South Asia Pte Ltd

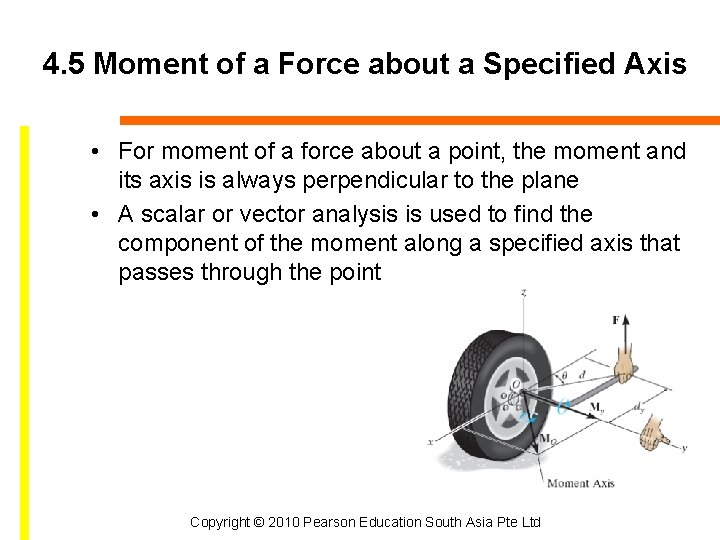
4. 5 Moment of a Force about a Specified Axis • For moment of a force about a point, the moment and its axis is always perpendicular to the plane • A scalar or vector analysis is used to find the component of the moment along a specified axis that passes through the point Copyright © 2010 Pearson Education South Asia Pte Ltd

4. 5 Moment of a Force about a Specified Axis Scalar Analysis • According to the right-hand rule, My is directed along the positive y axis • For any axis, the moment is • Force will not contribute a moment if force line of action is parallel or passes through the axis Copyright © 2010 Pearson Education South Asia Pte Ltd

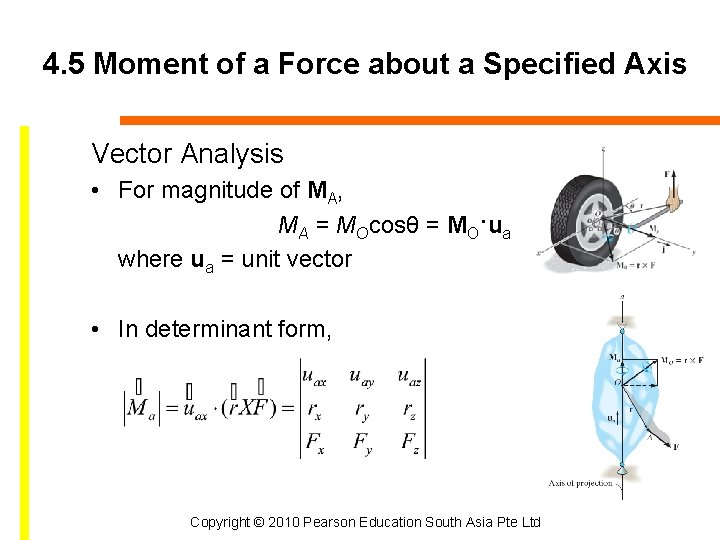
4. 5 Moment of a Force about a Specified Axis Vector Analysis • For magnitude of MA, MA = MOcosθ = MO·ua where ua = unit vector • In determinant form, Copyright © 2010 Pearson Education South Asia Pte Ltd

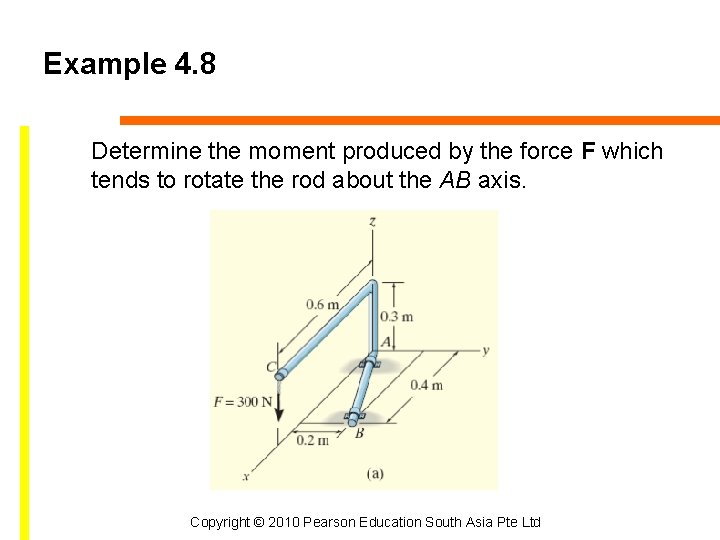
Example 4. 8 Determine the moment produced by the force F which tends to rotate the rod about the AB axis. Copyright © 2010 Pearson Education South Asia Pte Ltd

Solution Unit vector defines the direction of the AB axis of the rod, where For simplicity, choose r. D The force is Copyright © 2010 Pearson Education South Asia Pte Ltd

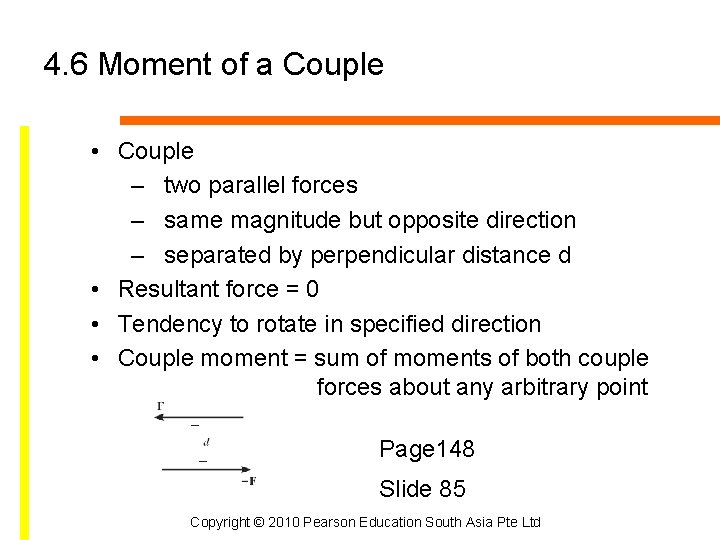
4. 6 Moment of a Couple • Couple – two parallel forces – same magnitude but opposite direction – separated by perpendicular distance d • Resultant force = 0 • Tendency to rotate in specified direction • Couple moment = sum of moments of both couple forces about any arbitrary point Page 148 Slide 85 Copyright © 2010 Pearson Education South Asia Pte Ltd

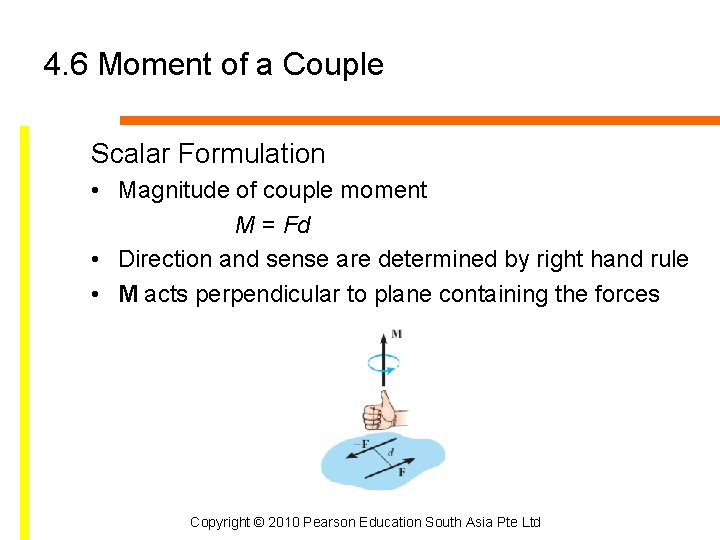
4. 6 Moment of a Couple Scalar Formulation • Magnitude of couple moment M = Fd • Direction and sense are determined by right hand rule • M acts perpendicular to plane containing the forces Copyright © 2010 Pearson Education South Asia Pte Ltd

4. 6 Moment of a Couple Vector Formulation • For couple moment, M=r. XF • If moments are taken about point A, moment of –F is zero about this point • r is crossed with the force to which it is directed Copyright © 2010 Pearson Education South Asia Pte Ltd

4. 6 Moment of a Couple Equivalent Couples • 2 couples are equivalent if they produce the same moment • Forces of equal couples lie on the same plane or plane parallel to one another Copyright © 2010 Pearson Education South Asia Pte Ltd

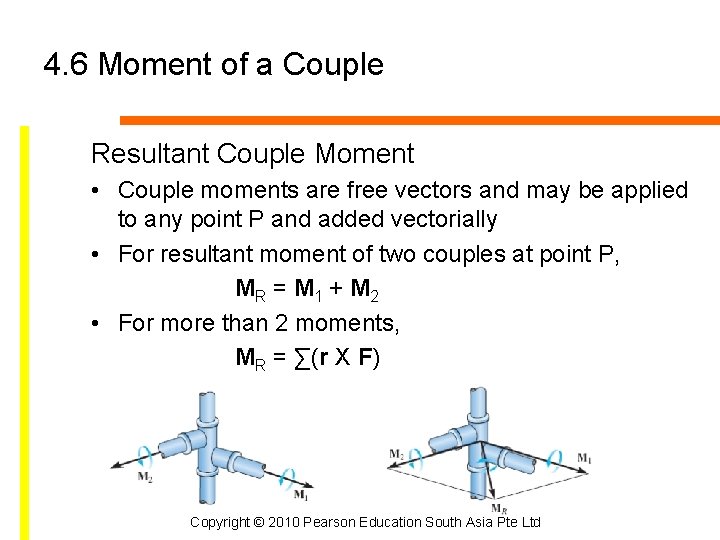
4. 6 Moment of a Couple Resultant Couple Moment • Couple moments are free vectors and may be applied to any point P and added vectorially • For resultant moment of two couples at point P, MR = M 1 + M 2 • For more than 2 moments, MR = ∑(r X F) Copyright © 2010 Pearson Education South Asia Pte Ltd

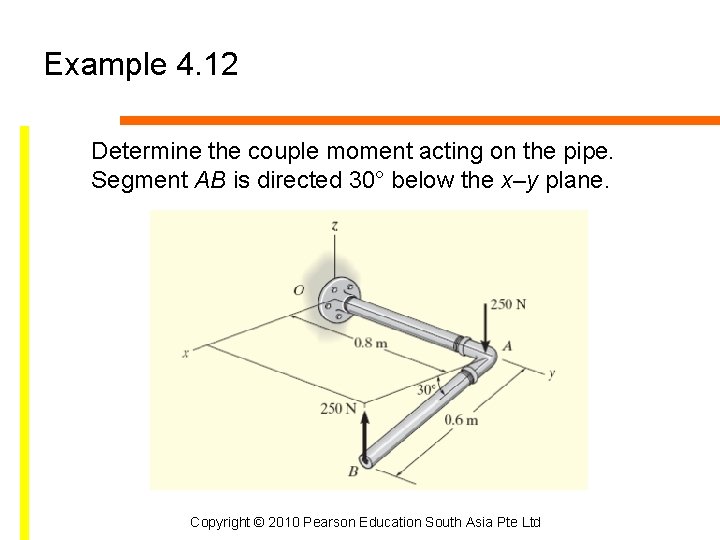
Example 4. 12 Determine the couple moment acting on the pipe. Segment AB is directed 30° below the x–y plane. Copyright © 2010 Pearson Education South Asia Pte Ltd

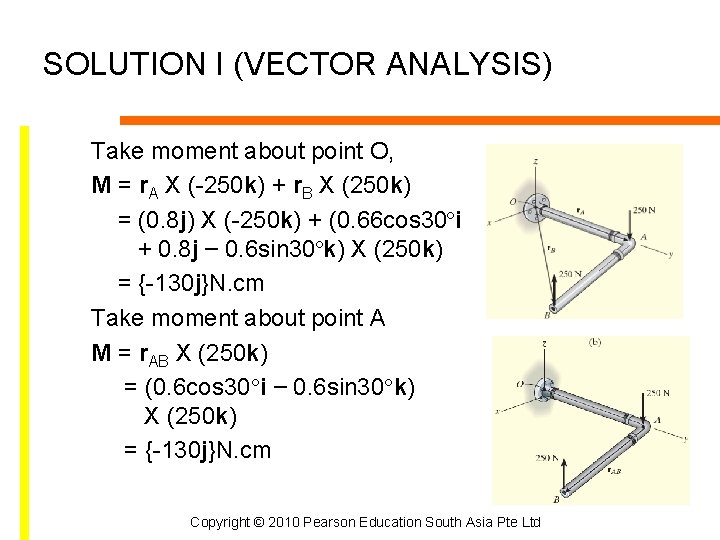
SOLUTION I (VECTOR ANALYSIS) Take moment about point O, M = r. A X (-250 k) + r. B X (250 k) = (0. 8 j) X (-250 k) + (0. 66 cos 30ºi + 0. 8 j – 0. 6 sin 30ºk) X (250 k) = {-130 j}N. cm Take moment about point A M = r. AB X (250 k) = (0. 6 cos 30°i – 0. 6 sin 30°k) X (250 k) = {-130 j}N. cm Copyright © 2010 Pearson Education South Asia Pte Ltd

SOLUTION II (SCALAR ANALYSIS) Take moment about point A or B, M = Fd = 250 N(0. 5196 m) = 129. 9 N. cm Apply right hand rule, M acts in the –j direction M = {-130 j}N. cm Copyright © 2010 Pearson Education South Asia Pte Ltd

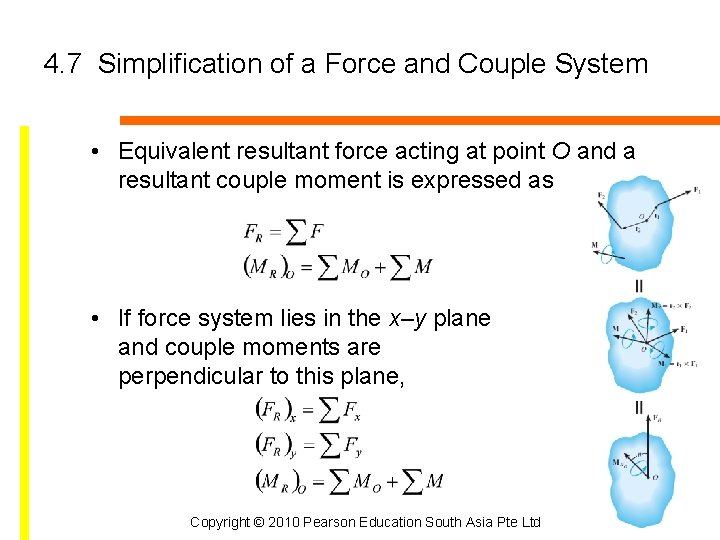
4. 7 Simplification of a Force and Couple System • An equivalent system is when the external effects are the same as those caused by the original force and couple moment system • External effects of a system is the translating and rotating motion of the body • Or refers to the reactive forces at the supports if the body is held fixed Copyright © 2010 Pearson Education South Asia Pte Ltd

4. 7 Simplification of a Force and Couple System • Equivalent resultant force acting at point O and a resultant couple moment is expressed as • If force system lies in the x–y plane and couple moments are perpendicular to this plane, Copyright © 2010 Pearson Education South Asia Pte Ltd

4. 7 Simplification of a Force and Couple System Procedure for Analysis 1. Establish the coordinate axes with the origin located at point O and the axes having a selected orientation 2. Force Summation 3. Moment Summation Copyright © 2010 Pearson Education South Asia Pte Ltd

Example 4. 16 A structural member is subjected to a couple moment M and forces F 1 and F 2. Replace this system with an equivalent resultant force and couple moment acting at its base, point O. Copyright © 2010 Pearson Education South Asia Pte Ltd

Solution Express the forces and couple moments as Cartesian vectors. Copyright © 2010 Pearson Education South Asia Pte Ltd

Solution Force Summation. Copyright © 2010 Pearson Education South Asia Pte Ltd

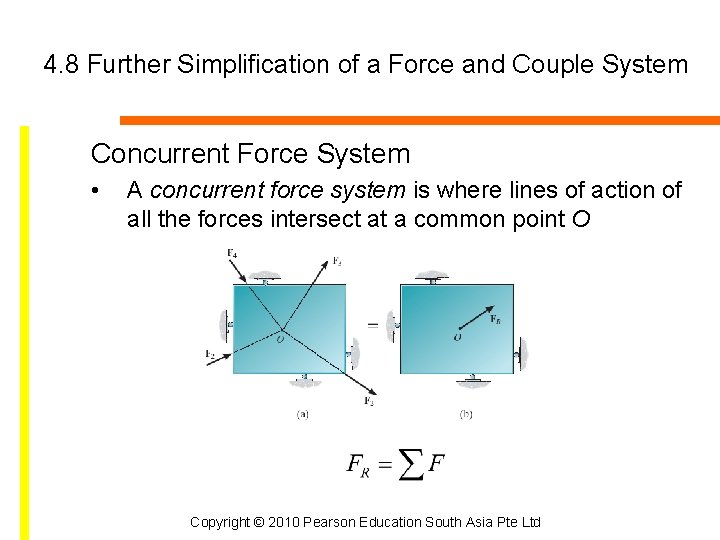
4. 8 Further Simplification of a Force and Couple System Concurrent Force System • A concurrent force system is where lines of action of all the forces intersect at a common point O Copyright © 2010 Pearson Education South Asia Pte Ltd

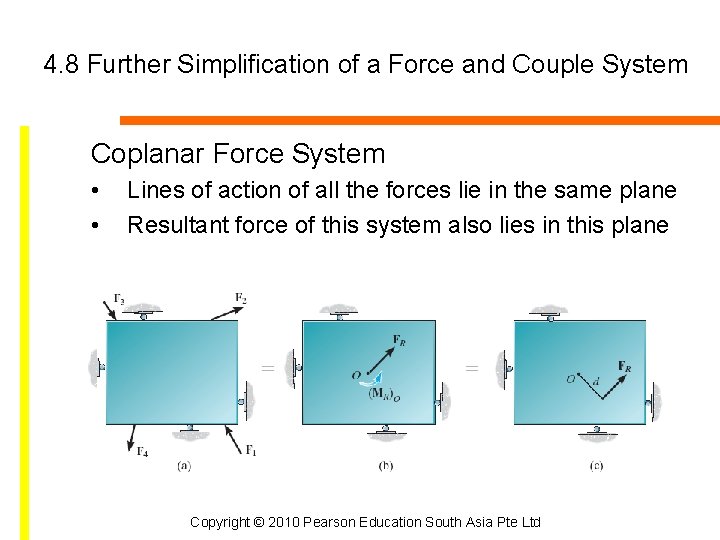
4. 8 Further Simplification of a Force and Couple System Coplanar Force System • • Lines of action of all the forces lie in the same plane Resultant force of this system also lies in this plane Copyright © 2010 Pearson Education South Asia Pte Ltd

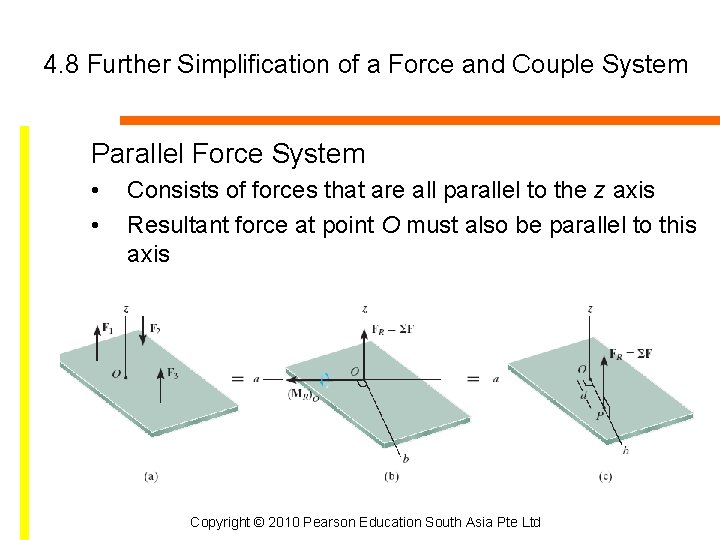
4. 8 Further Simplification of a Force and Couple System Parallel Force System • • Consists of forces that are all parallel to the z axis Resultant force at point O must also be parallel to this axis Copyright © 2010 Pearson Education South Asia Pte Ltd

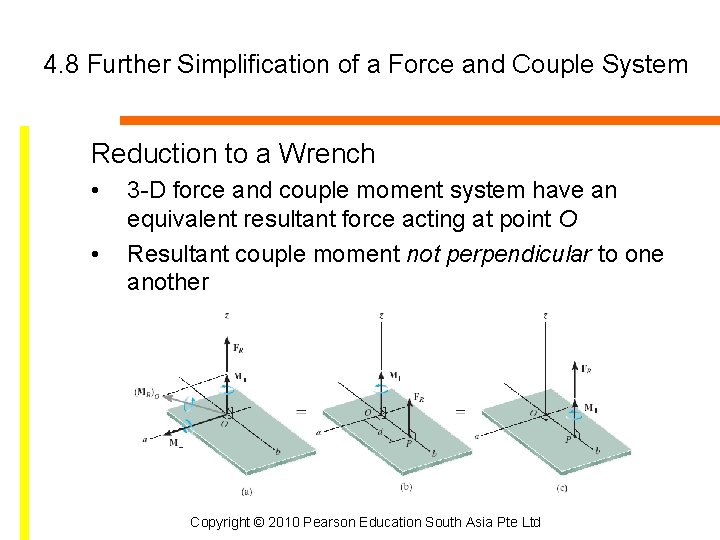
4. 8 Further Simplification of a Force and Couple System Reduction to a Wrench • • 3 -D force and couple moment system have an equivalent resultant force acting at point O Resultant couple moment not perpendicular to one another Copyright © 2010 Pearson Education South Asia Pte Ltd

Example 4. 18 The jib crane is subjected to three coplanar forces. Replace this loading by an equivalent resultant force and specify where the resultant’s line of action intersects the column AB and boom BC. Copyright © 2010 Pearson Education South Asia Pte Ltd

Solution Force Summation Copyright © 2010 Pearson Education South Asia Pte Ltd

Solution For magnitude of resultant force, FR = ( FRx )2 + ( FRy )2 = (3. 25)2 + (2. 60)2 = 4. 16 k. N For direction of resultant force, æF ö q = tan -1çç Ry ÷÷ = tan -1æç 2. 60 ö÷ è 3. 25 ø è FRx ø = 38. 7 o Copyright © 2010 Pearson Education South Asia Pte Ltd

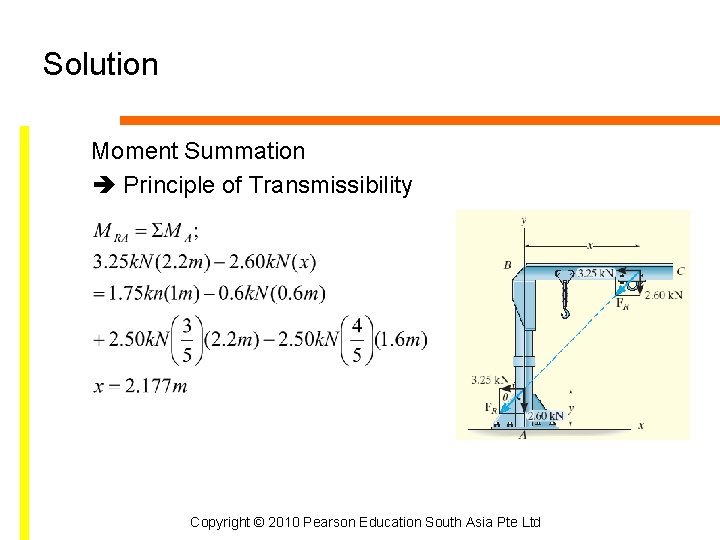
Solution Moment Summation of moments about point A, Copyright © 2010 Pearson Education South Asia Pte Ltd

Solution Moment Summation Principle of Transmissibility Copyright © 2010 Pearson Education South Asia Pte Ltd

4. 9 Reduction of a Simple Distributed Loading • Large surface area of a body may be subjected to distributed loadings • Loadings on the surface is defined as pressure • Pressure is measured in Pascal (Pa): 1 Pa = 1 N/m 2 Uniform Loading Along a Single Axis • Most common type of distributed loading is uniform along a single axis Copyright © 2010 Pearson Education South Asia Pte Ltd

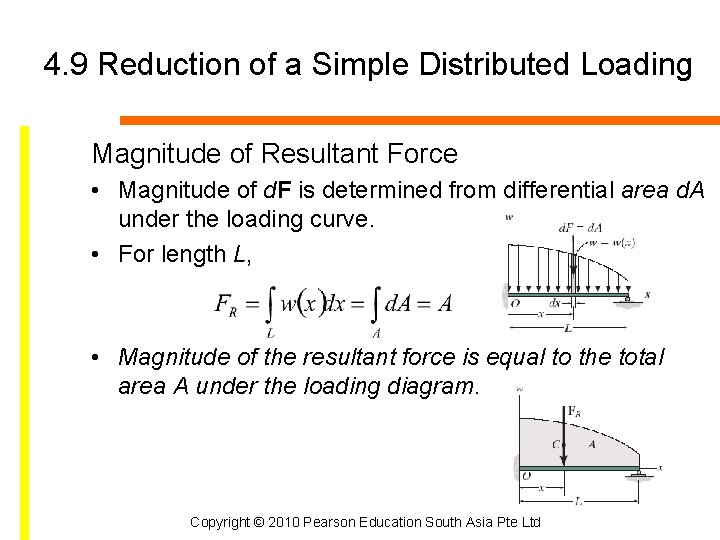
4. 9 Reduction of a Simple Distributed Loading Magnitude of Resultant Force • Magnitude of d. F is determined from differential area d. A under the loading curve. • For length L, • Magnitude of the resultant force is equal to the total area A under the loading diagram. Copyright © 2010 Pearson Education South Asia Pte Ltd

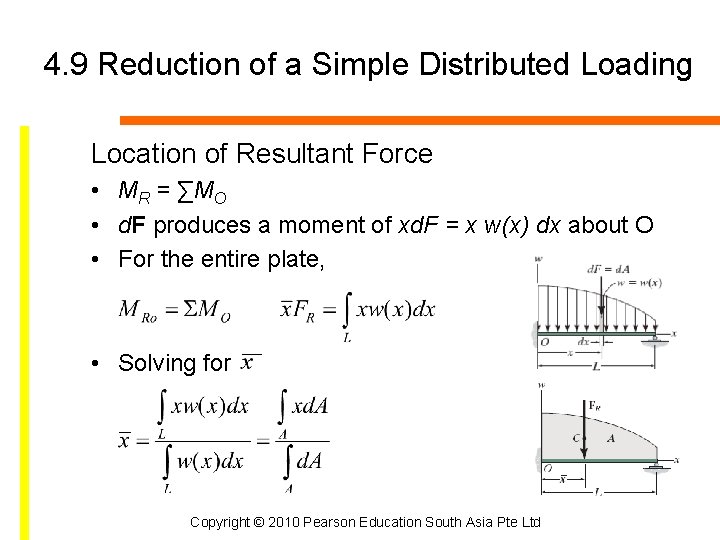
4. 9 Reduction of a Simple Distributed Loading Location of Resultant Force • MR = ∑MO • d. F produces a moment of xd. F = x w(x) dx about O • For the entire plate, • Solving for Copyright © 2010 Pearson Education South Asia Pte Ltd

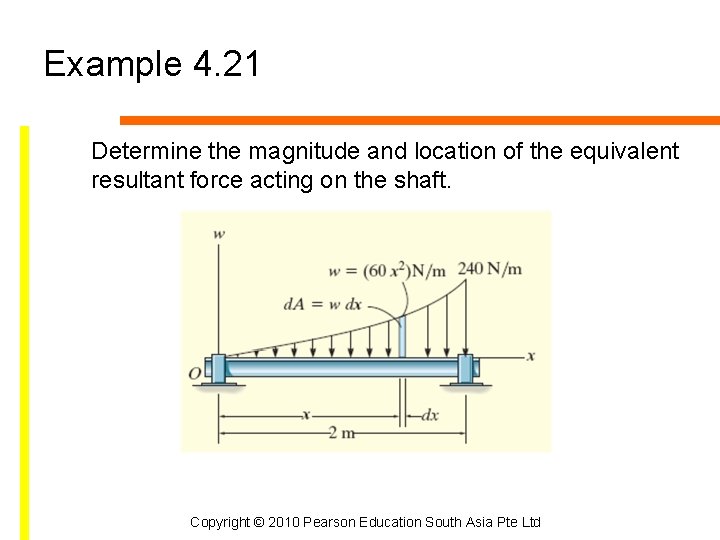
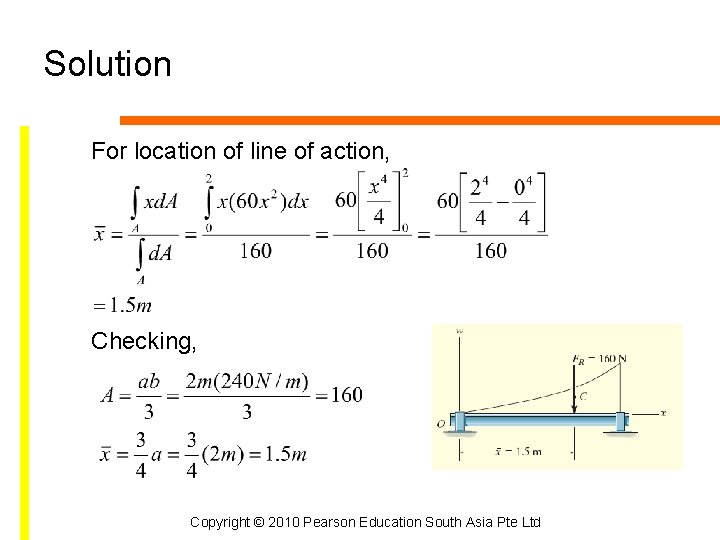
Example 4. 21 Determine the magnitude and location of the equivalent resultant force acting on the shaft. Copyright © 2010 Pearson Education South Asia Pte Ltd

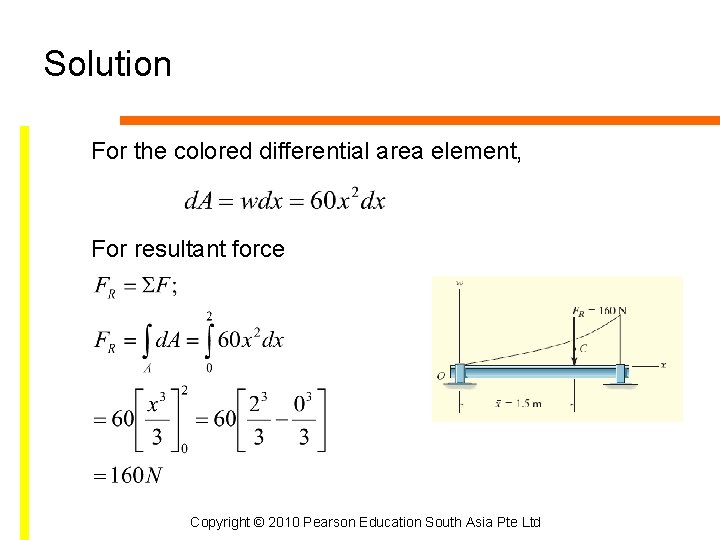
Solution For the colored differential area element, For resultant force Copyright © 2010 Pearson Education South Asia Pte Ltd

Solution For location of line of action, Checking, Copyright © 2010 Pearson Education South Asia Pte Ltd

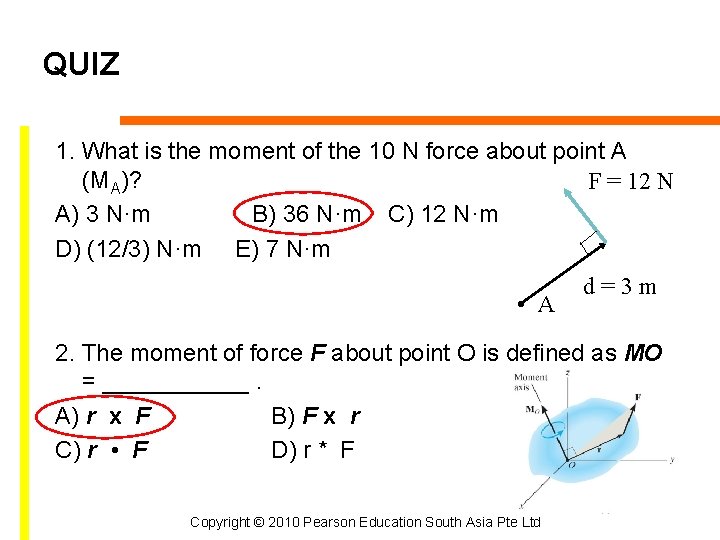
QUIZ 1. What is the moment of the 10 N force about point A (MA)? F = 12 N A) 3 N·m B) 36 N·m C) 12 N·m D) (12/3) N·m E) 7 N·m • A d=3 m 2. The moment of force F about point O is defined as MO = ______. A) r x F B) F x r C) r • F D) r * F Copyright © 2010 Pearson Education South Asia Pte Ltd

QUIZ 3. If a force of magnitude F can be applied in 4 different 2 D configurations (P, Q, R, & S), select the cases resulting in the maximum and minimum torque values on the nut. (Max, Min). A) (Q, P) B) (R, S) C) (P, R) D) (Q, S) 4. If M = r F, then what will be the value of M • r ? A) 0 B) 1 C) r 2 F D) None of the above. Copyright © 2010 Pearson Education South Asia Pte Ltd

QUIZ 5. Using the CCW direction as positive, the net moment of the two forces about point P is A) 10 N ·m B) 20 N ·m C) - 20 N ·m D) 40 N ·m E) - 40 N ·m 10 N 3 m P 2 m 5 N 6. If r = { 5 j } m and F = { 10 k } N, the moment r x F equals { _______ } N·m. A) 50 i B) 50 j C) – 50 i D) – 50 j E) 0 Copyright © 2010 Pearson Education South Asia Pte Ltd

QUIZ 7. When determining the moment of a force about a specified axis, the axis must be along _______. A) the x axis B) the y axis C) the z axis D) any line in 3 -D space E) any line in the x-y plane 8. The triple scalar product u • ( r F ) results in A) a scalar quantity ( + or - ) B) a vector quantity. C) zero. D) a unit vector. E) an imaginary number. Copyright © 2010 Pearson Education South Asia Pte Ltd

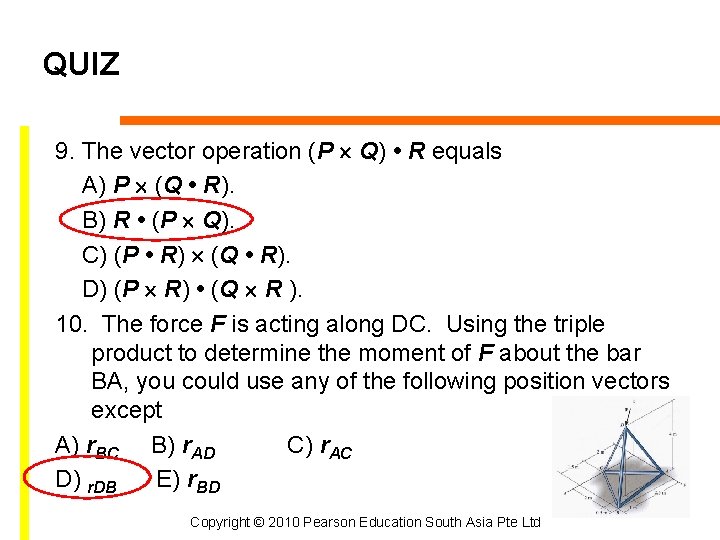
QUIZ 9. The vector operation (P Q) • R equals A) P (Q • R). B) R • (P Q). C) (P • R) (Q • R). D) (P R) • (Q R ). 10. The force F is acting along DC. Using the triple product to determine the moment of F about the bar BA, you could use any of the following position vectors except A) r. BC B) r. AD C) r. AC D) r. DB E) r. BD Copyright © 2010 Pearson Education South Asia Pte Ltd

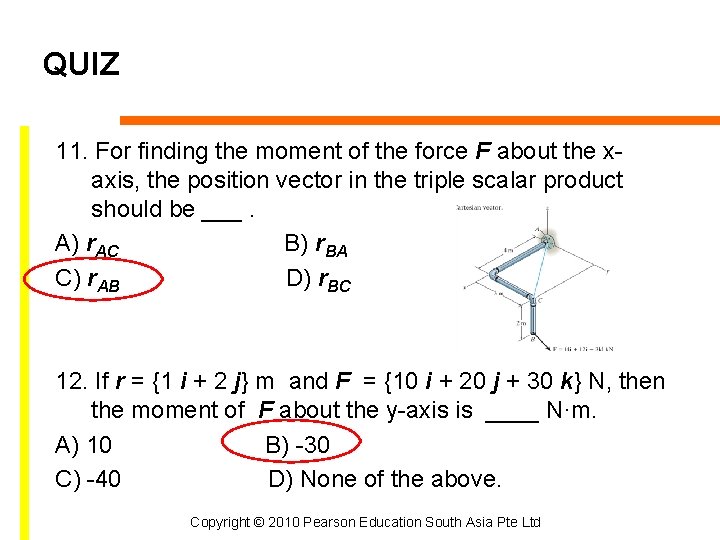
QUIZ 11. For finding the moment of the force F about the xaxis, the position vector in the triple scalar product should be ___. A) r. AC B) r. BA C) r. AB D) r. BC 12. If r = {1 i + 2 j} m and F = {10 i + 20 j + 30 k} N, then the moment of F about the y-axis is ____ N·m. A) 10 B) -30 C) -40 D) None of the above. Copyright © 2010 Pearson Education South Asia Pte Ltd

QUIZ 13. In statics, a couple is defined as _____ separated by a perpendicular distance. A) two forces in the same direction B) two forces of equal magnitude C) two forces of equal magnitude acting in the same direction D) two forces of equal magnitude acting in opposite directions 14. The moment of a couple is called a _____ vector. A) Free B) Spin C) Romantic D) Sliding Copyright © 2010 Pearson Education South Asia Pte Ltd

QUIZ 15. F 1 and F 2 form a couple. The moment of the couple is given by ____. A) r 1 F 1 B) r 2 F 1 C) F 2 r 1 D) r 2 F 2 16. If three couples act on a body, the overall result is that A) The net force is not equal to 0. B) The net force and net moment are equal to 0. C) The net moment equals 0 but the net force is not necessarily equal to 0. D) The net force equals 0 but the net moment is not necessarily equal to 0. Copyright © 2010 Pearson Education South Asia Pte Ltd

QUIZ 17. A general system of forces and couple moments acting on a rigid body can be reduced to a ___. A) single force B) single moment C) single force and two moments D) single force and a single moment 18. The original force and couple system and an equivalent force-couple system have the same _____ effect on a body. A) internal B) external C) internal and external D) microscopic Copyright © 2010 Pearson Education South Asia Pte Ltd

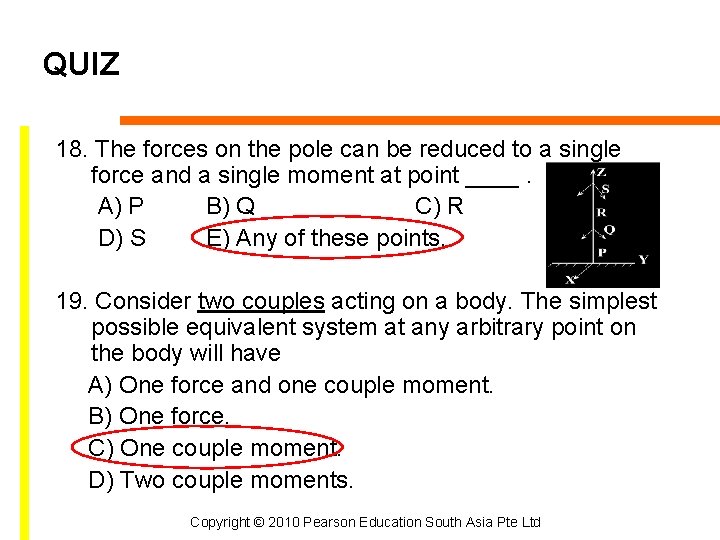
QUIZ 18. The forces on the pole can be reduced to a single force and a single moment at point ____. A) P B) Q C) R D) S E) Any of these points. 19. Consider two couples acting on a body. The simplest possible equivalent system at any arbitrary point on the body will have A) One force and one couple moment. B) One force. C) One couple moment. D) Two couple moments. Copyright © 2010 Pearson Education South Asia Pte Ltd

QUIZ 20. Consider three couples acting on a body. Equivalent systems will be _______ at different points on the body. A) Different when located B) The same even when located C) Zero when located D) None of the above. Copyright © 2010 Pearson Education South Asia Pte Ltd

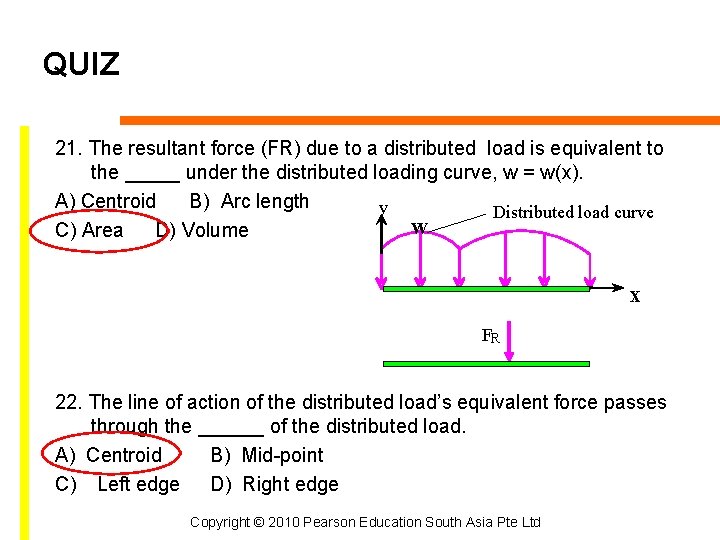
QUIZ 21. The resultant force (FR) due to a distributed load is equivalent to the _____ under the distributed loading curve, w = w(x). A) Centroid B) Arc length y Distributed load curve w C) Area D) Volume x FR 22. The line of action of the distributed load’s equivalent force passes through the ______ of the distributed load. A) Centroid B) Mid-point C) Left edge D) Right edge Copyright © 2010 Pearson Education South Asia Pte Ltd

QUIZ 23. What is the location of FR, i. e. , the distance d? A) 2 m B) 3 m C) 4 m D) 5 m. E) 6 m A BA 3 m 3 m FR d B 24. If F 1 = 1 N, x 1 = 1 m, F 2 = 2 N and x 2 = 2 m, what is the location of FR, i. e. , the distance x. A) 1 m B) 1. 33 m C) 1. 5 m F 1 x 2 x FR F 2 D) 1. 67 m E) 2 m x 1 Copyright © 2010 Pearson Education South Asia Pte Ltd

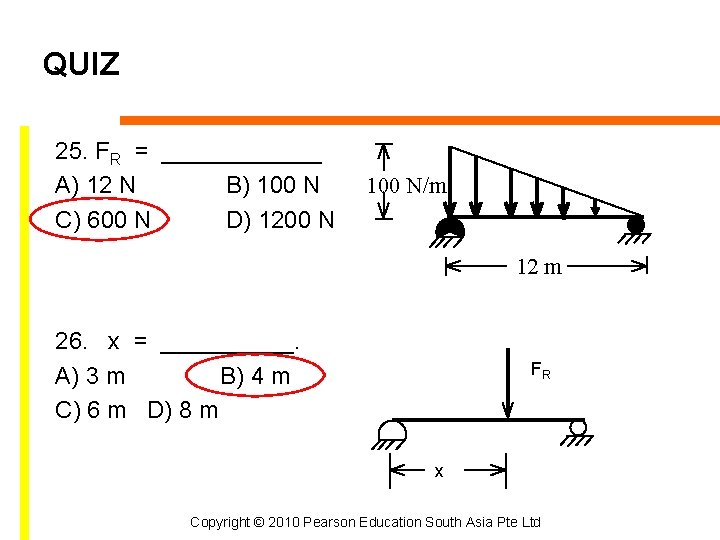
QUIZ 25. FR = ______ A) 12 N B) 100 N C) 600 N D) 1200 N 100 N/m 12 m 26. x = _____. A) 3 m B) 4 m C) 6 m D) 8 m FR x Copyright © 2010 Pearson Education South Asia Pte Ltd