ENGINEERING MECHANICS STATICS Equilibrium of particle in space

ENGINEERING MECHANICS STATICS

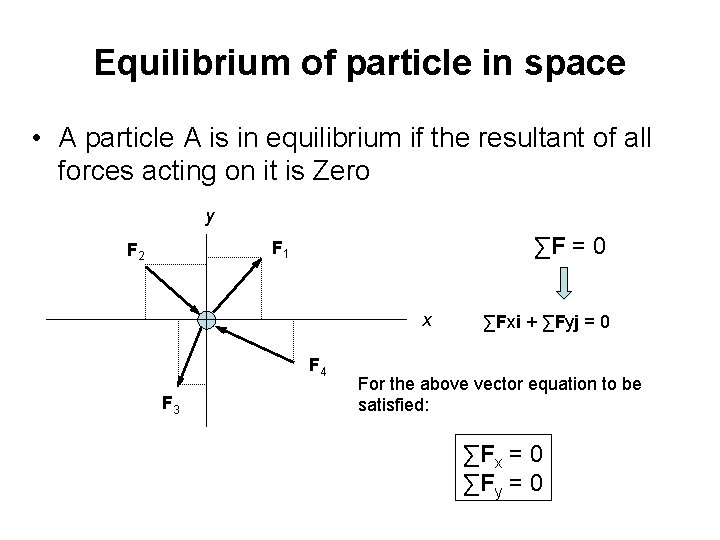
Equilibrium of particle in space • A particle A is in equilibrium if the resultant of all forces acting on it is Zero y ∑F = 0 F 1 F 2 x F 4 F 3 ∑Fxi + ∑Fyj = 0 For the above vector equation to be satisfied: ∑Fx = 0 ∑Fy = 0

Equilibrium of a Particle • When the resultant of all forces acting on a particle is zero, the particle is in equilibrium. • Newton’s First Law: If the resultant force on a particle is zero, the particle will remain at rest or will continue at constant speed in a straight line. • Particle acted upon by two forces: - equal magnitude - same line of action - opposite sense • Particle acted upon by three or more forces: - graphical solution yields a closed polygon - algebraic solution

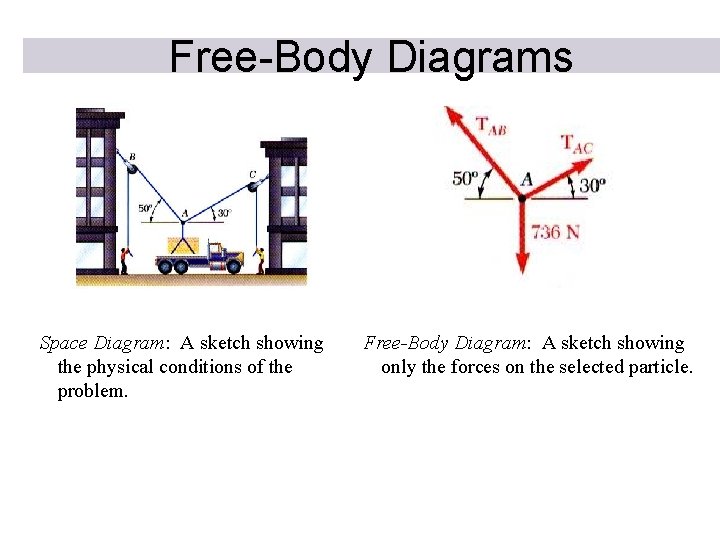
Free-Body Diagrams Space Diagram: A sketch showing the physical conditions of the problem. Free-Body Diagram: A sketch showing only the forces on the selected particle.

THE WHAT, WHY AND HOW OF A FREE BODY DIAGRAM (FBD) Free Body Diagrams are one of the most important things for you to know how to draw and use. What ? - It is a drawing that shows all external forces acting on the particle. Why ? - It helps you write the equations of equilibrium used to solve for the unknowns (usually forces or angles).

How ? 1. Imagine the particle to be isolated or cut free from its surroundings. 2. Show all the forces that act on the particle. Active forces: They want to move the particle. Reactive forces: They tend to resist the motion. 3. Identify each force and show all known magnitudes and directions. Show all unknown magnitudes and / or directions as variables.

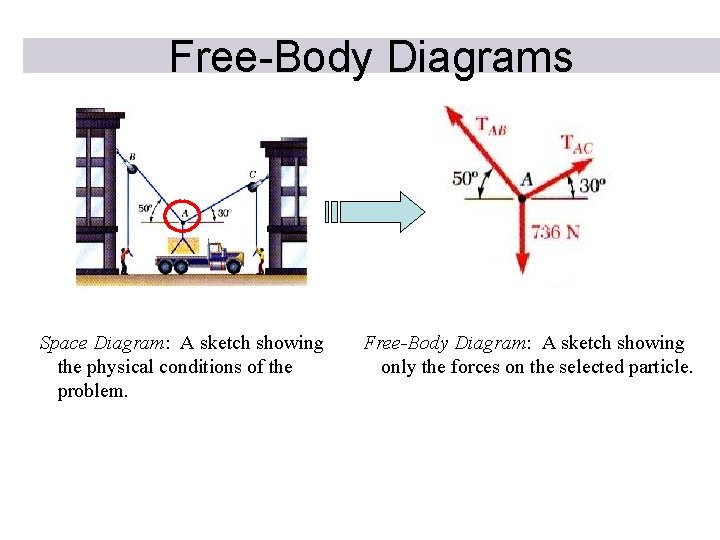
Free-Body Diagrams Space Diagram: A sketch showing the physical conditions of the problem. Free-Body Diagram: A sketch showing only the forces on the selected particle.

Equilibrium of particle in space three dimensional force system For equilibrium we require: ∑F = 0 Resolving forces into their respective i, j, k components, we get ∑Fxi + ∑Fyj + ∑Fzk = 0 ∑Fx = 0 ∑Fy = 0 ∑Fz = 0

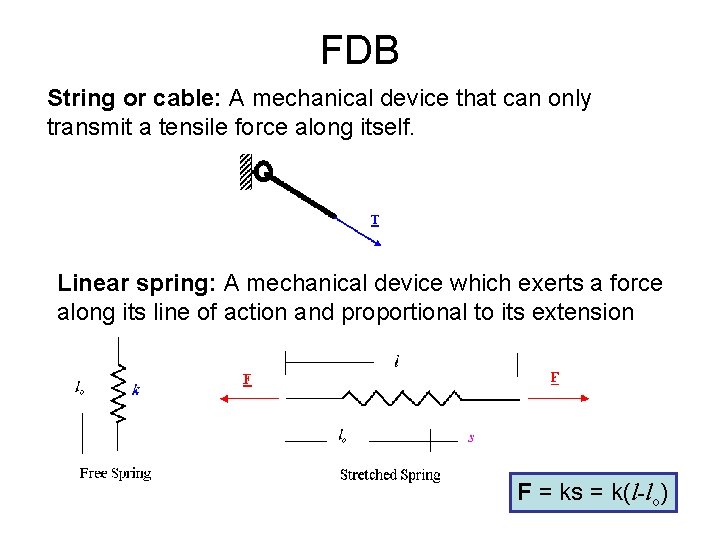
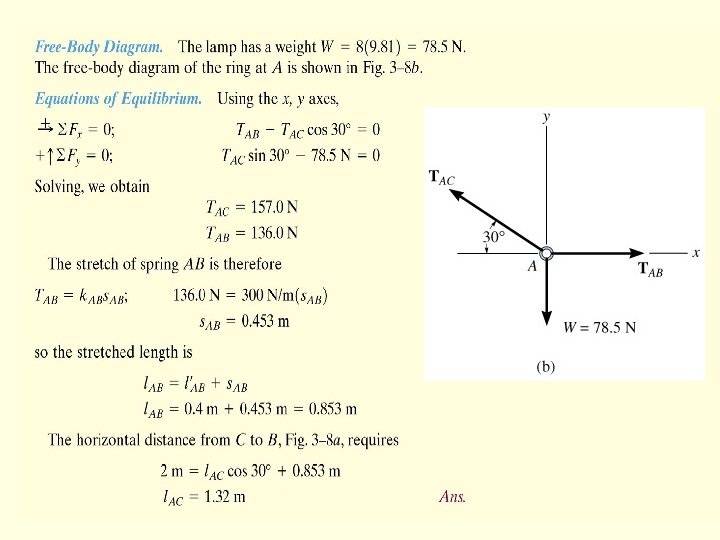
FDB String or cable: A mechanical device that can only transmit a tensile force along itself. Linear spring: A mechanical device which exerts a force along its line of action and proportional to its extension F = ks = k(l-lo)

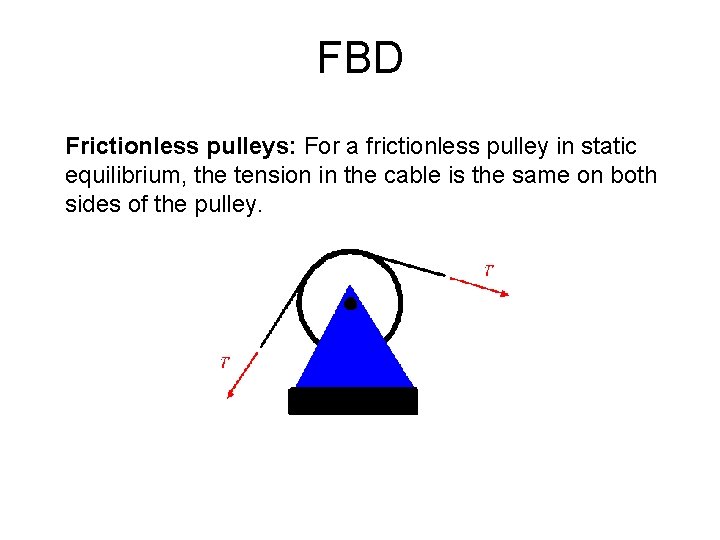
FBD Frictionless pulleys: For a frictionless pulley in static equilibrium, the tension in the cable is the same on both sides of the pulley.

Example FBD

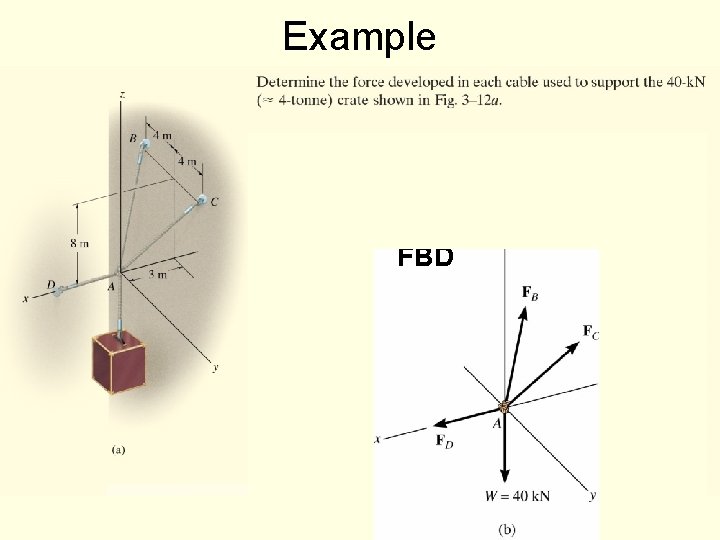
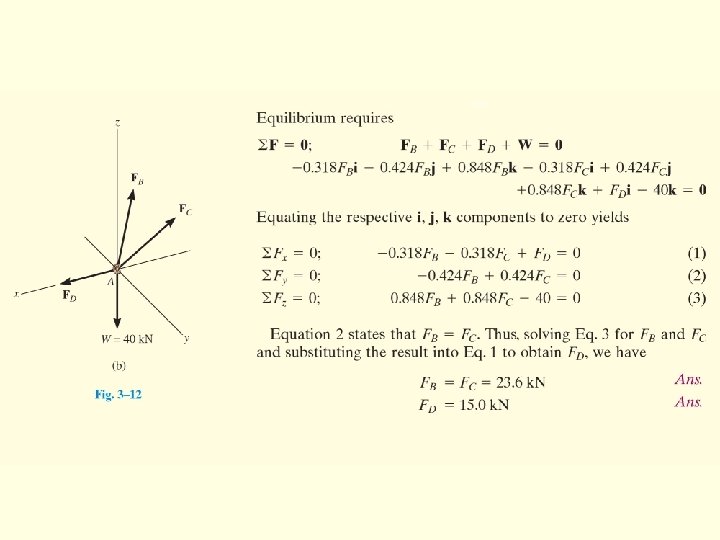
Example FBD

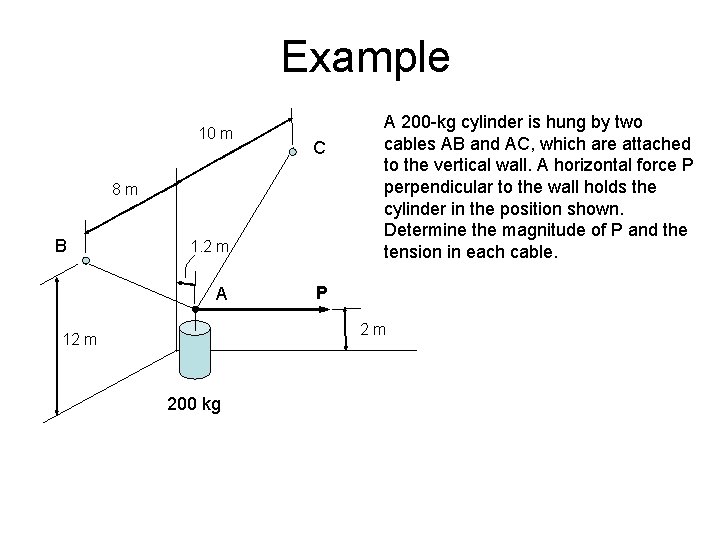
Example 10 m C 8 m B 1. 2 m A A 200 -kg cylinder is hung by two cables AB and AC, which are attached to the vertical wall. A horizontal force P perpendicular to the wall holds the cylinder in the position shown. Determine the magnitude of P and the tension in each cable. P 2 m 12 m 200 kg

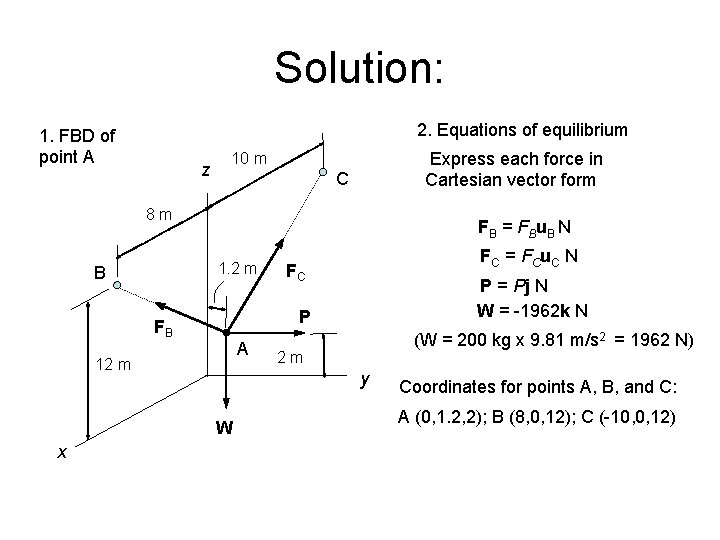
Solution: 2. Equations of equilibrium 1. FBD of point A z Express each force in Cartesian vector form 10 m C 8 m FB = FBu. B N 1. 2 m B FC P = Pj N W = -1962 k N P FB A 12 m (W = 200 kg x 9. 81 m/s 2 = 1962 N) 2 m y W x FC = FC u. C N Coordinates for points A, B, and C: A (0, 1. 2, 2); B (8, 0, 12); C (-10, 0, 12)