ENGINEERING MECHANICS MOMENT OF INERTIA Prepared by Dr

ENGINEERING MECHANICS MOMENT OF INERTIA Prepared by, Dr. S. Elangovan Mr. N. Muthuram Department of Production Engineering PSG College of Technology Coimbatore – 641004. This work is licensed under the Creative Commons Attribution 4. 0 International License. To view a copy of this license, visit http: //creativecommons. org/licenses/by/4. 0/ or send a letter to Creative Commons, PO Box 1866, Mountain View, CA 94042, USA.

MOMENT OF INERTIA The moment of inertia of an object is a measure of its resistance to change in rotation or capacity of a cross section to resist bending. . Example: It is harder to start (or stop) a large wheel turning than a small wheel • large wheel having a larger moment of inertia. Applications: Moments of inertia are used in various engineering calculations: • Locating the resultant of hydrostatic pressure forces on submerged bodies • Calculating stresses in beams – resistance to bending • Mass moments of inertia are used in studying the rotational motion of objects

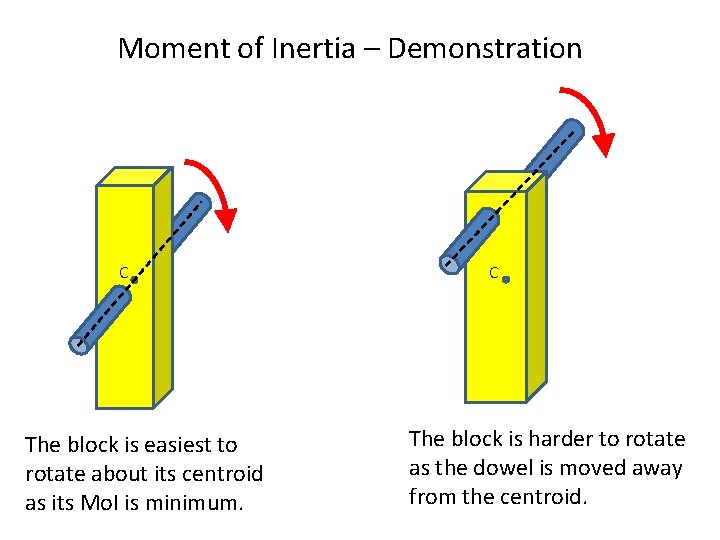
Moment of Inertia – Demonstration C The block is easiest to rotate about its centroid as its Mo. I is minimum. C The block is harder to rotate as the dowel is moved away from the centroid.

MOMENT OF INERTIA The product of the elemental area and square of the perpendicular distance between the centroid of area and the axis of reference is the “Moment of Inertia” about the reference axis. It is also called second moment of area because first moment of elemental area is d. A. y and d. A. x; and if it is again multiplied by the distance, we get second moment of elemental area as (d. A. y)y and (d. A. x)x. Ixx = ∫d. A. Y 2 Iyy = ∫d. A. x 2

Polar moment of Inertia (Perpendicular Axes theorem) • The moment of inertia of an area about an axis perpendicular to the plane of the area is called “Polar Moment of Inertia” and it is denoted by symbol Izz or J or Ip. (or) • The moment of inertia of an area about an axis perpendicular to its plane (Polar M. I) at any point O is equal to the sum of moments of inertia about any two mutually perpendicular axis through the same point O and lying in the plane of the area.

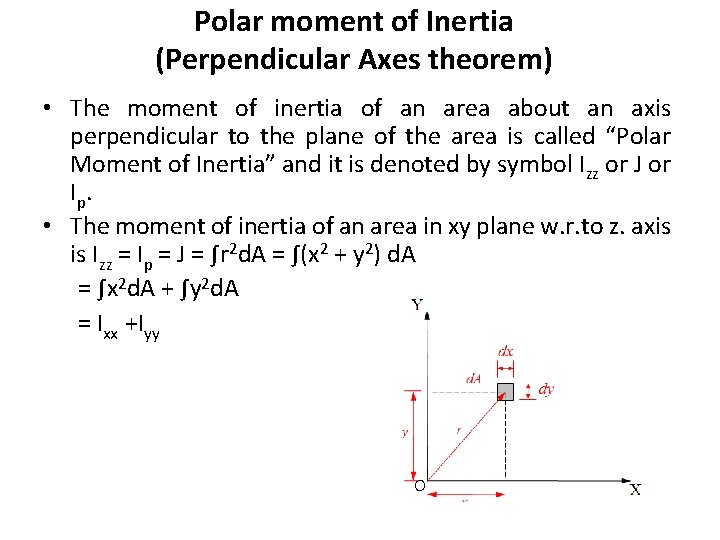
Polar moment of Inertia (Perpendicular Axes theorem) • The moment of inertia of an area about an axis perpendicular to the plane of the area is called “Polar Moment of Inertia” and it is denoted by symbol Izz or J or I p. • The moment of inertia of an area in xy plane w. r. to z. axis is Izz = Ip = J = ∫r 2 d. A = ∫(x 2 + y 2) d. A = ∫x 2 d. A + ∫y 2 d. A = Ixx +Iyy O

Parallel Axis Theorem Moment of inertia about any axis in the plane of an area is equal to the sum of moment of inertia about a parallel centroidal axis and the product of area and square of the distance between the two parallel axes.

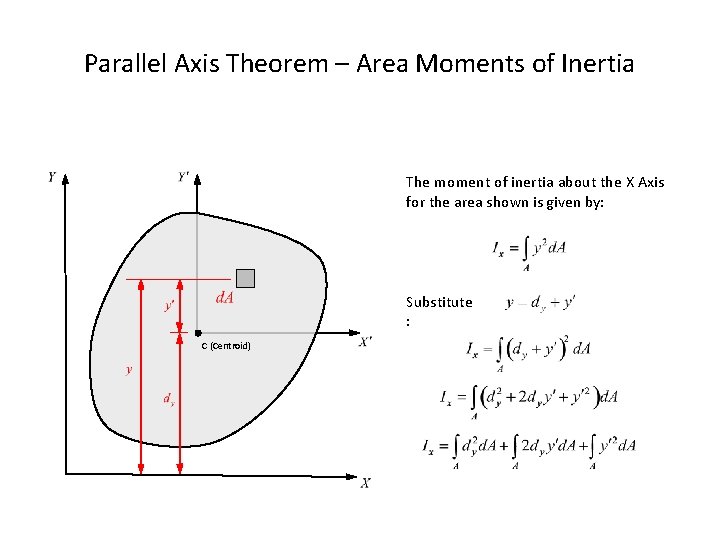
Parallel Axis Theorem – Area Moments of Inertia The moment of inertia about the X Axis for the area shown is given by: Substitute : C (Centroid)

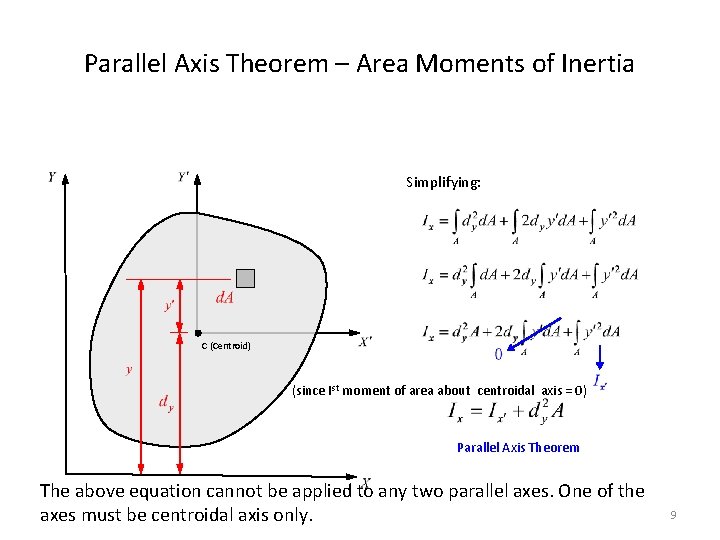
Parallel Axis Theorem – Area Moments of Inertia Simplifying: C (Centroid) (since Ist moment of area about centroidal axis = 0) Parallel Axis Theorem The above equation cannot be applied to any two parallel axes. One of the axes must be centroidal axis only. 9

Radius of Gyration It is the perpendicular distance at which the whole area may be assumed to be concentrated, yielding the same second moment of the area above the axis under consideration.

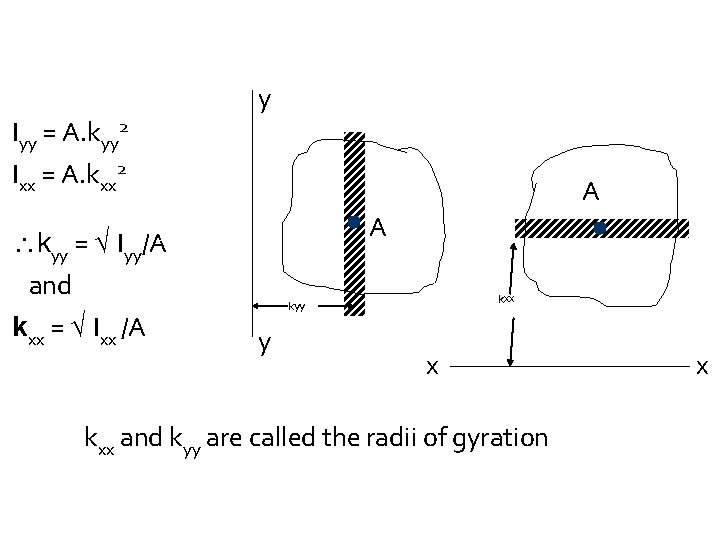
Iyy = A. kyy 2 y Ixx = A. kxx 2 kyy = √ Iyy/A and kxx = √ Ixx /A A A kxx kyy y x kxx and kyy are called the radii of gyration x

Thank you