Engineering Mechanics LECTURE 29 By D V Ramana

Engineering Mechanics LECTURE 29 By D. V. Ramana Reddy Assistant Professor Department of Mechanical Engineering

Lecture 29 TOPICS : Centre of gravity of simple and complex shapes

Centre of Gravity

Centre of gravity
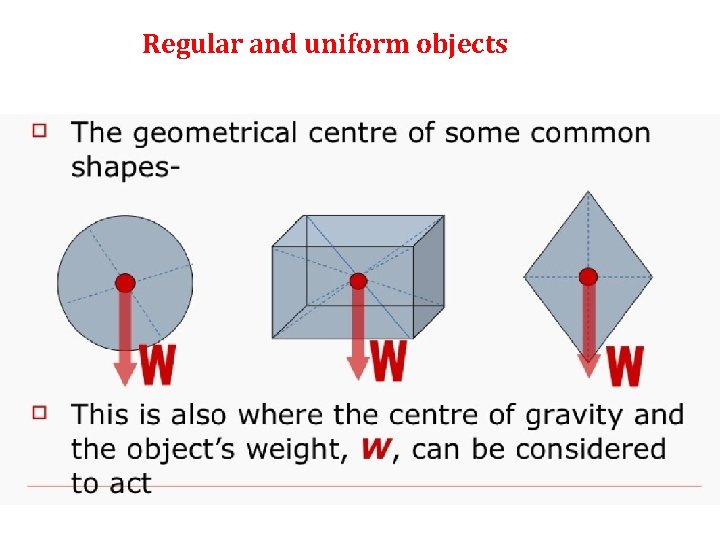
Regular and uniform objects
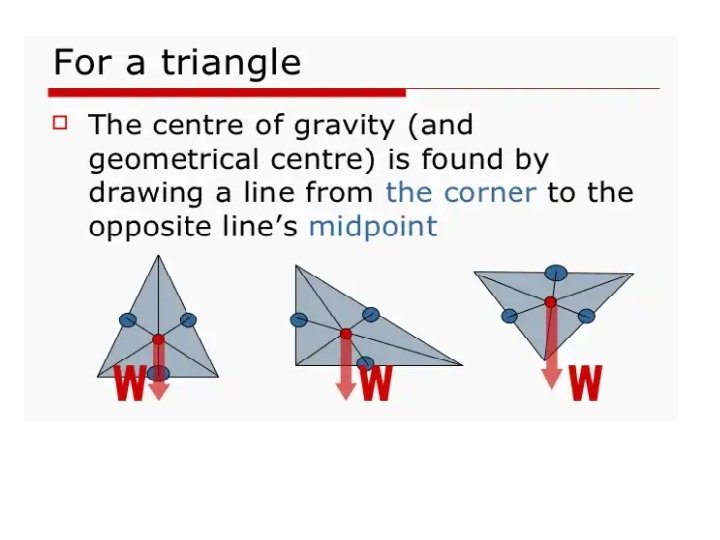
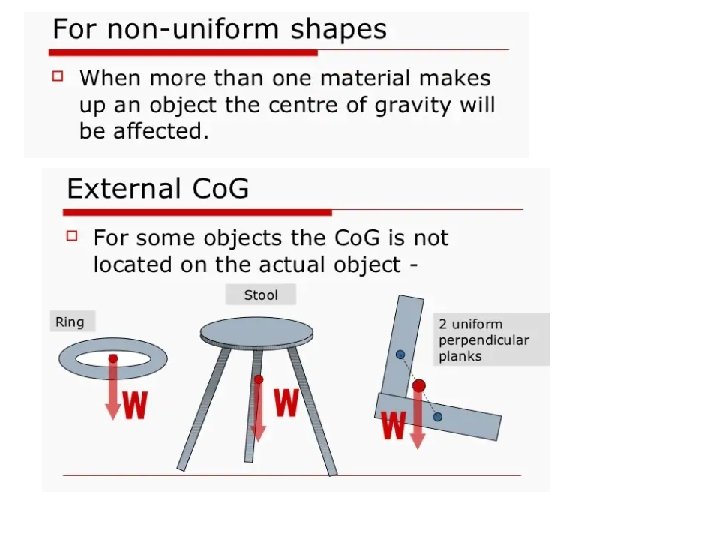
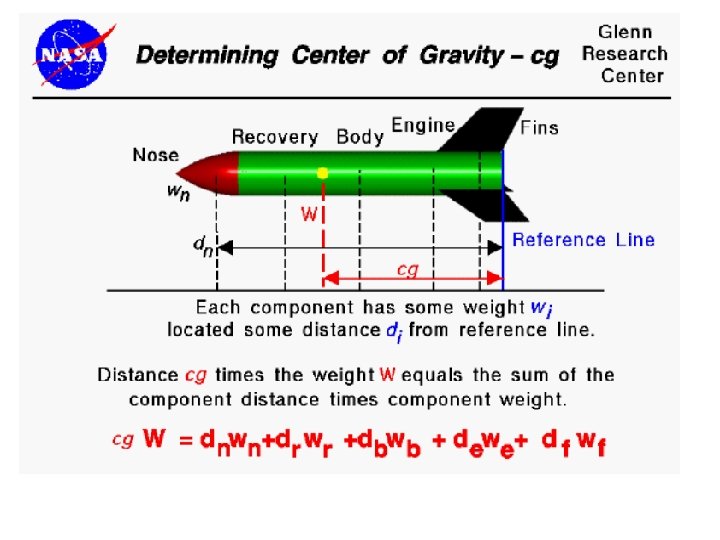

Centre of gravity
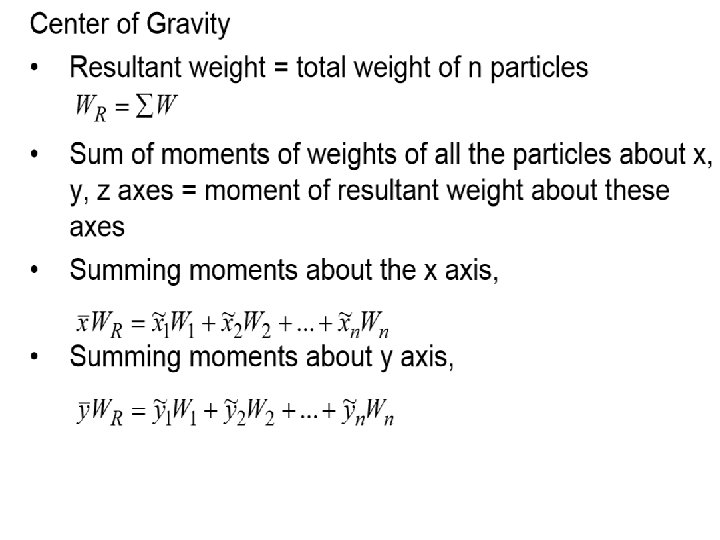
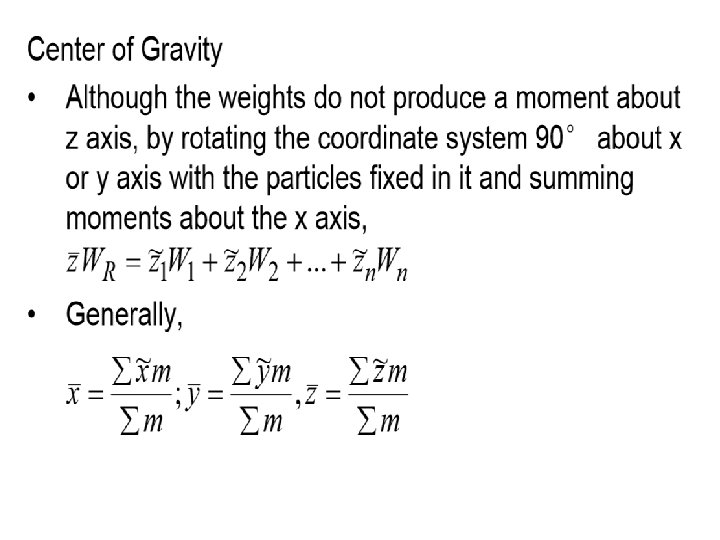
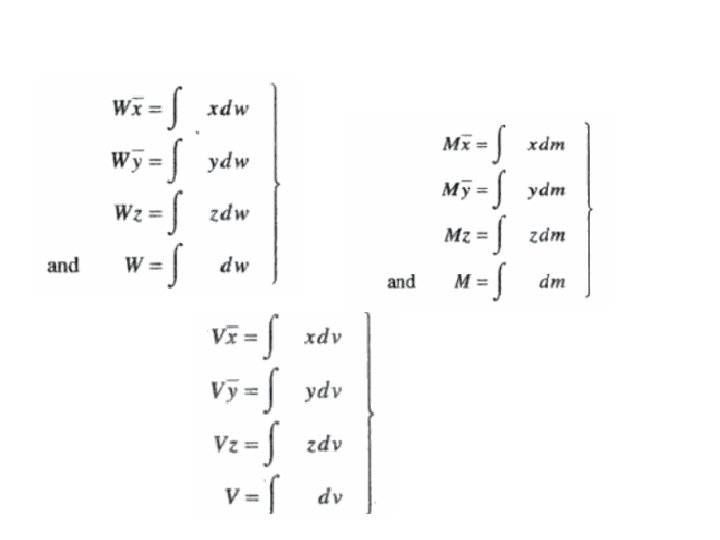

Centre of mass
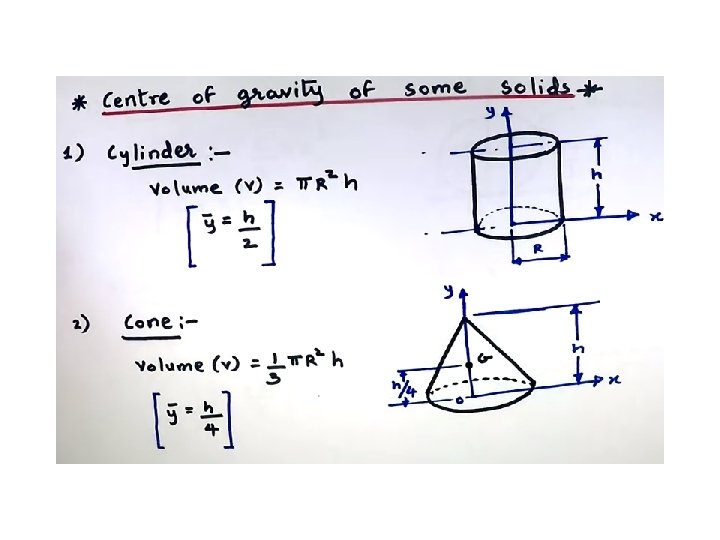

Locate the centre of gravity of Right circular cone base radius r and height h Taking origin at the vertex of the cone and selecting the axes as shown in fig. it can be observed that due to symmetry the coordinates of centre of gravity y and z coordinates are equal to zero. The centre of gravity lies on the axis of rotation of the cone.
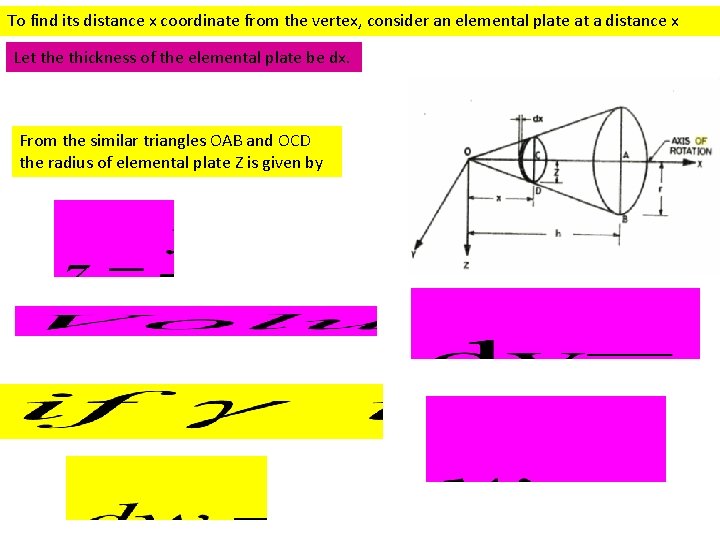
To find its distance x coordinate from the vertex, consider an elemental plate at a distance x Let the thickness of the elemental plate be dx. From the similar triangles OAB and OCD the radius of elemental plate Z is given by
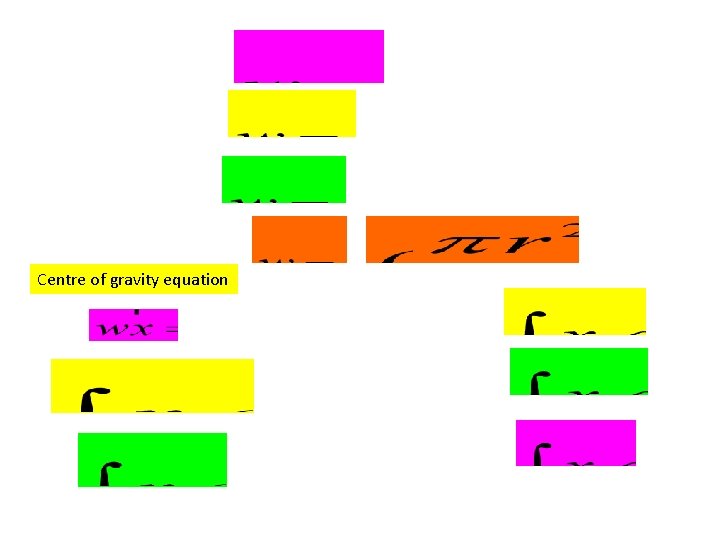
Centre of gravity equation
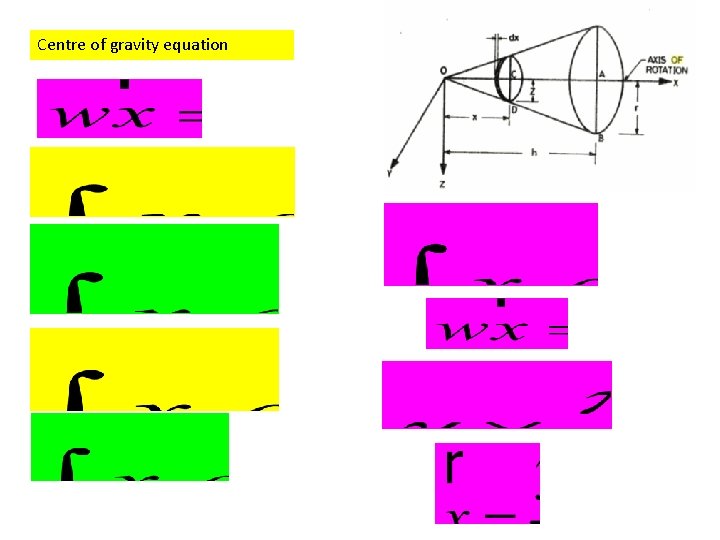
Centre of gravity equation

Conclusion: In a right circular cone, centre of gravity lies at a distance 3 h/4 from vertex along the axis of rotation and at a distance of h/4 from the base.

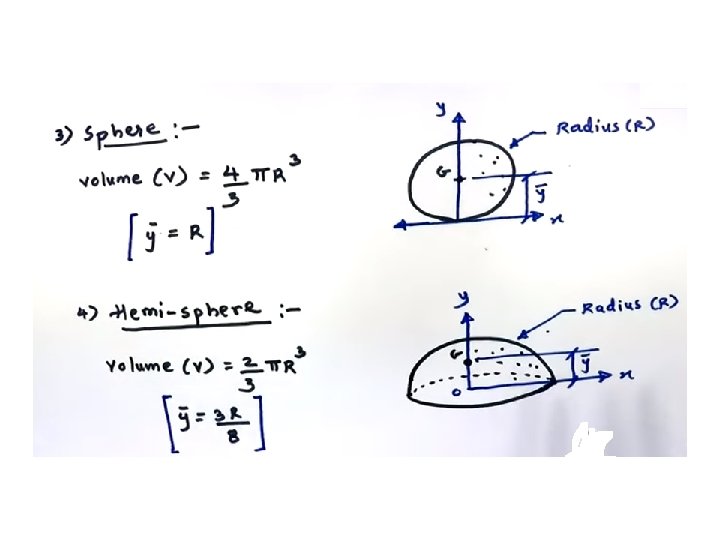
CENTRE OF GRAVITY OF SOLID HEMISPHERE Centre of gravity of a solid hemisphere of radius r from its diametral axis Due to symmetry centre of gravity lies on the axis of rotation To find its distance x coordinate from the base along axis of rotation Consider an elemental plate at a distance x as shown in fig.
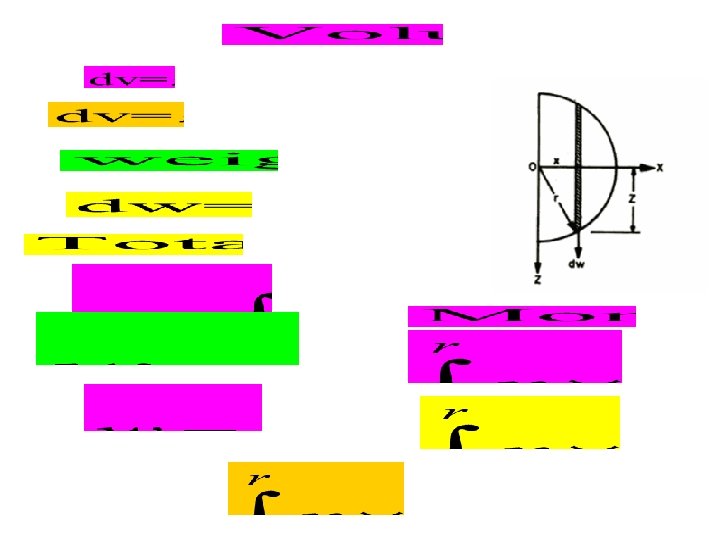
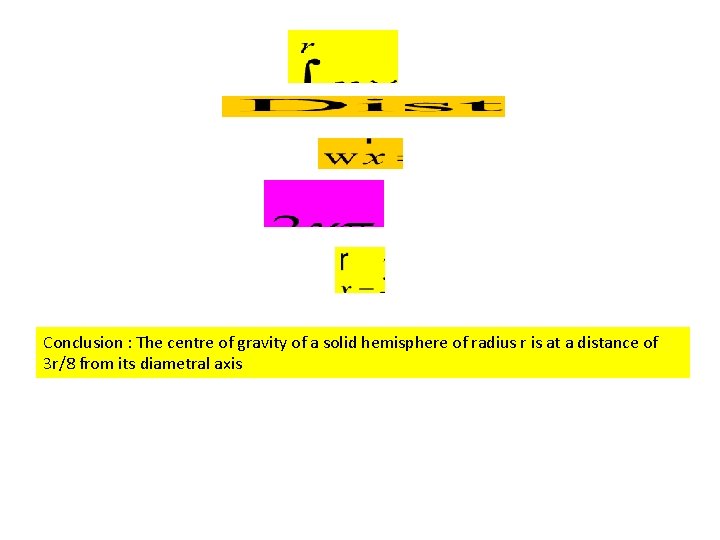
Conclusion : The centre of gravity of a solid hemisphere of radius r is at a distance of 3 r/8 from its diametral axis
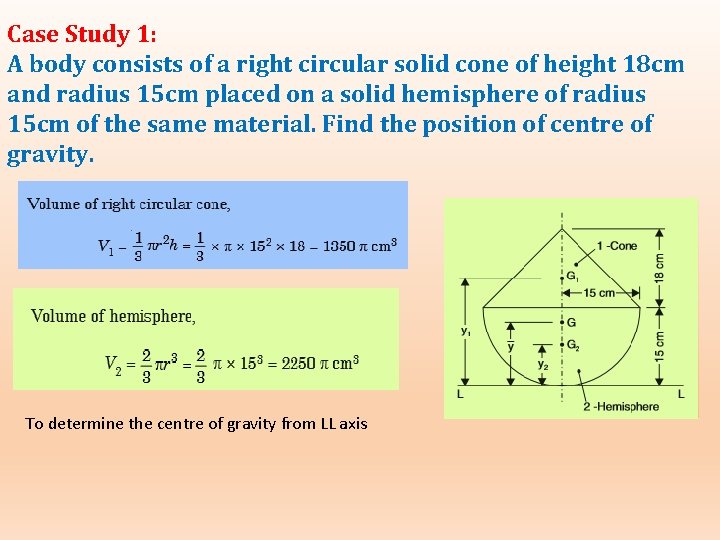
Case Study 1: A body consists of a right circular solid cone of height 18 cm and radius 15 cm placed on a solid hemisphere of radius 15 cm of the same material. Find the position of centre of gravity. To determine the centre of gravity from LL axis

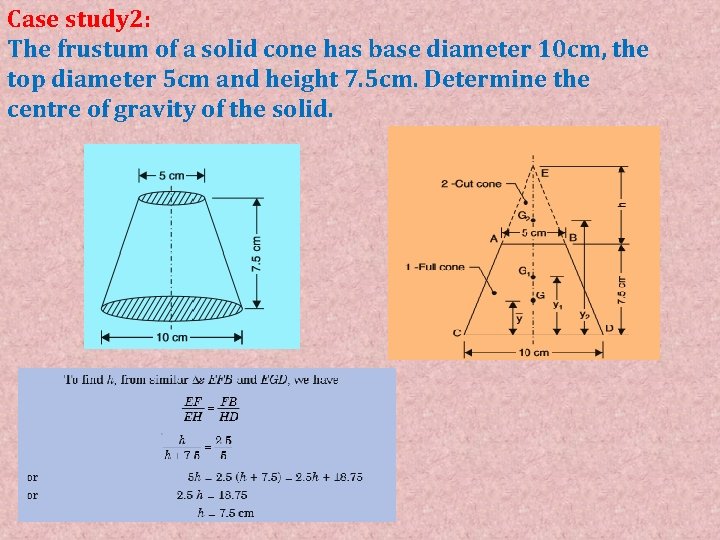
Case study 2: The frustum of a solid cone has base diameter 10 cm, the top diameter 5 cm and height 7. 5 cm. Determine the centre of gravity of the solid.


Homework: : A right circular cylinder of 12 cm diameter is joined with a hemisphere of the same diameter face to face. Find the greatest height of the cylinder, so that centre of gravity of the composite section coincides with the plane of joining the two sections. The density of the material of hemisphere is twice that the material of cylinder.


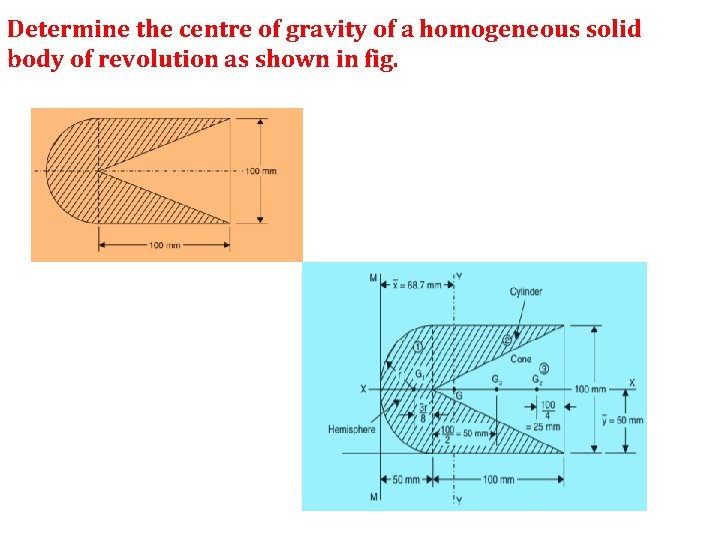
Determine the centre of gravity of a homogeneous solid body of revolution as shown in fig.

- Slides: 33