Engineering Mechanics LECTURE 02 VECTORS C 2005 Pearson

Chapter Outline Scalars & Vectors Rules for Manipulating Vectors Components in 2 Dimensions Dot

2. 1 Scalars & Vectors Scalar – a physical quantity that is completely described

2. 1 Scalars & Vectors ◦ Graphical representation of vectors: arrows Direction of arrow

2. 2 Rules for Manipulating Vectors Vector Addition: ◦ When an object undergoes a

2. 2 Rules for Manipulating Vectors ◦ 2 nd displacement V ◦ Final position

2. 2 Rules for Manipulating Vectors Definition of Vector Addition: ◦ Vector from tail

2. 2 Rules for Manipulating Vectors ◦ Vector addition is commutative: U+V=V+U (2. 1)

2. 2 Rules for Manipulating Vectors n Product of a Scalar & a Vector:

2. 2 Rules for Manipulating Vectors ◦ The product is associative with respect to

2. 2 Rules for Manipulating Vectors Vector Subtraction: U – V = U +

Example 2. 1 Adding Vectors Fig. 2. 11 is an initial design sketch of

Example 2. 1 Adding Vectors Strategy (a) By drawing the parallelogram rule for adding

Example 2. 1 Adding Vectors Solution (a) Graphically construct the parallelogram rule with FAB

Example 2. 1 Adding Vectors Solution (b) Consider the parallelogram rule: Since + 30°

Example 2. 1 Adding Vectors Solution (b) To determine the angle between FAB +

Example 2. 1 Adding Vectors Critical Thinking n n n In engineering applications, vector

2. 3 Components in 2 Dimensions Vectors are much easier to work with when

2. 3 Components in 2 Dimensions ◦ Introduce a unit vector i defined to

2. 3 Components in 2 Dimensions Manipulating Vectors in Terms of Components: ◦ Sum

2. 3 Components in 2 Dimensions Manipulating Vectors in Terms of Components: ◦ Product

2. 3 Components in 2 Dimensions Position Vectors in Terms of Components: ◦ Consider

2. 3 Components in 2 Dimensions Position Vectors in Terms of Components: ◦ Let

Example 2. 2 Adding Vectors in Terms of Components The forces acting on the

Example 2. 2 Adding Vectors in Terms of Components Strategy (a) By letting the

Example 2. 2 Adding Vectors in Terms of Components Solution (a) Set the sum

Example 2. 2 Adding Vectors in Terms of Components Solution (b) If the drag

Example 2. 3 Determining Components in Terms of an Angle Hydraulic cylinders are used

Example 2. 3 Determining Components in Terms of an Angle Strategy When the direction

Example 2. 3 Determining Components in Terms of an Angle Solution Magnitude of Fx:

Example 2. 3 Determining Components in Terms of an Angle Solution Fy points in

Example 2. 3 Determining Components in Terms of an Angle Critical Thinking n When

Example 2. 4 Determining Components The cable from point A to point B exerts

Example 2. 4 Determining Components Strategy 1 st Method: ◦ Determine the angle between

Example 2. 4 Determining Components Strategy 3 rd Method: ◦ Determine the components of

Example 2. 4 Determining Components Solution 1 st Method: Consider the force F &

Example 2. 4 Determining Components Solution n 1 st Method: From the right triangles

Example 2. 4 Determining Components Solution n 1 st Method: Since Fx points in

Example 2. 4 Determining Components Solution 2 nd Method: Length of cable AB: Since

Example 2. 4 Determining Components Solution 2 nd Method: (C) 2005 Pearson Education South

Example 2. 4 Determining Components Solution n 2 nd Method: Also from similar triangles:

Example 2. 4 Determining Components Solution 3 rd Method: Vector r. AB: (C) 2005

Example 2. 4 Determining Components Solution n 3 rd Method: Divide this vector by

Example 2. 4 Determining Components Solution § 3 rd Method: The force F is

Example 2. 4 Determining Components Critical Thinking To specify a vector, the magnitude &

Example 2. 4 Determining Components Critical Thinking 2 nd Method: ◦ Take advantage of

Example 2. 5 Determining an unknown Vector Magnitude The cables A & B in

Example 2. 5 Determining an unknown Vector Magnitude Strategy The vector sum of the

Example 2. 5 Determining an unknown Vector Magnitude Solution (a) Total force: Set the

Example 2. 5 Determining an unknown Vector Magnitude Solution (b) With |FB|, the total

Example 2. 5 Determining an unknown Vector Magnitude Critical Thinking We can obtain the

Slides: 51

Download presentation

2. 1 Scalars & Vectors Scalar – a physical quantity that is completely described by a real number ◦ E. g. Time, mass Vector – both magnitude (nonnegative real number) & direction ◦ E. g. Position of a point in space relative to another point, forces ◦ Represented by boldfaced letters: ◦ Magnitude of vector (C) 2005 Pearson Education South Asia Pte Ltd 3

2. 1 Scalars & Vectors ◦ Graphical representation of vectors: arrows Direction of arrow = direction of vector Length of arrow n (a) (b) Example: Ø r. AB = position of point B relative to point A Ø Direction of r. AB = direction from point A to point B Ø |r. AB| = distance between 2 points (C) 2005 Pearson Education South Asia Pte Ltd 4

2. 2 Rules for Manipulating Vectors Vector Addition: ◦ When an object undergoes a displacement (moves from 1 location in space to another) ◦ Displacement vector: U ◦ Direction of U = direction of displacement ◦ |U| = distance the book moves (C) 2005 Pearson Education South Asia Pte Ltd 5

2. 2 Rules for Manipulating Vectors ◦ 2 nd displacement V ◦ Final position of book is the same whether we give it displacement U then V, or vice versa ◦ U and V equivalent to a single displacement W: U + V = W (C) 2005 Pearson Education South Asia Pte Ltd 6

2. 2 Rules for Manipulating Vectors Definition of Vector Addition: ◦ Vector from tail of U to head of V Triangle rule ◦ Sum is independent of the order in which the vectors are placed head to tail Parallelogram rule (C) 2005 Pearson Education South Asia Pte Ltd 7

2. 2 Rules for Manipulating Vectors ◦ Vector addition is commutative: U+V=V+U (2. 1) ◦ Vector addition is associative: (U + V) + W = U + (V + W) (2. 2) ◦ If the sum of 2 or more vectors = 0, they form a closed polygon ◦ Example: Vector r. AC from A to C is the & r. BC sum of r. AB (C) 2005 Pearson Education South Asia Pte Ltd 8

2. 2 Rules for Manipulating Vectors n Product of a Scalar & a Vector: Ø Product of scalar (real number) a & vector U = vector a. U Ø Magnitude = |a||U| , where |a| is the absolute value of the scalar a Ø Direction of a. U is the same as direction of U when a is positive Ø Direction of a. U is opposite to direction of U when a is negative Ø Division of a vector U by a scalar a: (C) 2005 Pearson Education South Asia Pte Ltd 9

2. 2 Rules for Manipulating Vectors ◦ The product is associative with respect to scalar multiplication: a(b. U) = (ab)U (2. 3) ◦ The product is distributive with respect to scalar addition: (a + b)U = a. U + b. U (2. 4) ◦ The product is distributive with respect to vector addition: a(U + V) = a. U + a. V (2. 5) (C) 2005 Pearson Education South Asia Pte Ltd 10

2. 2 Rules for Manipulating Vectors Vector Subtraction: U – V = U + ( 1)V Unit (2. 6) Vectors: ◦ Magnitude = 1 ◦ Specifies a direction ◦ If a unit vector e & a vector U have the same direction: U = |U|e Unit Vector Subtraction (C) 2005 Pearson Education South Asia Pte Ltd 11

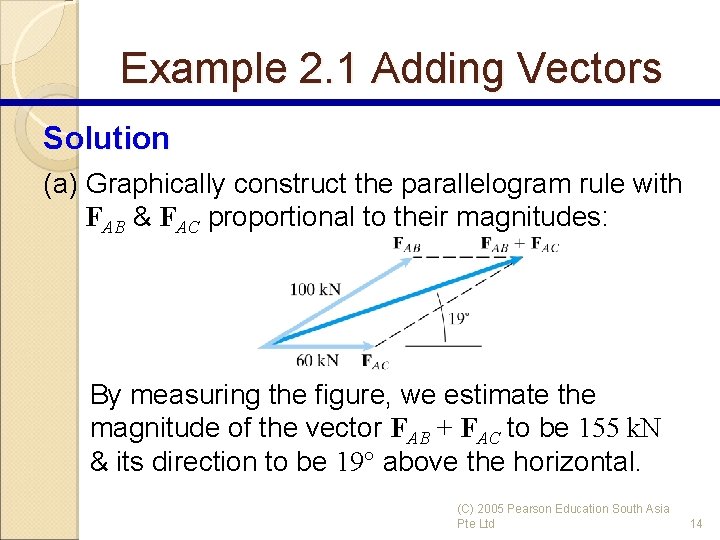
Example 2. 1 Adding Vectors Fig. 2. 11 is an initial design sketch of part of the roof of a sports stadium to be supported by the cables AB & AC. The forces the cables exert on the pylon to which they are attached are represented by the vectors FAB & FAC. The magnitude of the forces are |FAB| = 100 k. N & |FAC| = 60 k. N. Determine the magnitude & direction of the sum of the forces exerted on the pylon by the cables (a) graphically & (b) using trigonometry. Figure 2. 11 (C) 2005 Pearson Education South Asia Pte Ltd 12

Example 2. 1 Adding Vectors Strategy (a) By drawing the parallelogram rule for adding the 2 forces with the vectors drawn to scale, we can measure the magnitude & direction of their sum. (b) We will calculate the magnitude & direction of the sum of the forces by applying the laws of sines & cosines to the triangles formed by the parallelogram rule. (C) 2005 Pearson Education South Asia Pte Ltd 13

Example 2. 1 Adding Vectors Solution (a) Graphically construct the parallelogram rule with FAB & FAC proportional to their magnitudes: By measuring the figure, we estimate the magnitude of the vector FAB + FAC to be 155 k. N & its direction to be 19° above the horizontal. (C) 2005 Pearson Education South Asia Pte Ltd 14

Example 2. 1 Adding Vectors Solution (b) Consider the parallelogram rule: Since + 30° = 180°, = 150° Applying law of cosines to shaded triangle: Magnitude |FAB + FAC| = 155 k. N (C) 2005 Pearson Education South Asia Pte Ltd 15

Example 2. 1 Adding Vectors Solution (b) To determine the angle between FAB + FAC & the horizontal, apply law of sines to shaded triangle: The solution is (C) 2005 Pearson Education South Asia Pte Ltd 16

Example 2. 1 Adding Vectors Critical Thinking n n n In engineering applications, vector operations are nearly always done analytically However, graphical methods enhances your intuition about vectors & helps you understand vector operations Also, sketching out a graphical solution can often help you to formulate an analytical solution (C) 2005 Pearson Education South Asia Pte Ltd 17

2. 3 Components in 2 Dimensions Vectors are much easier to work with when expressed in terms of mutually perpendicular vector components: ◦ Consider vector U: ◦ Place a cartesian coordinate system so that the vector U is parallel to the x-y plane ◦ U = sum of perpendicular vector components Ux & Uy that are parallel to the x & y axes: U = Ux + Uy (C) 2005 Pearson Education South Asia Pte Ltd 18

2. 3 Components in 2 Dimensions ◦ Introduce a unit vector i defined to point in the direction of the positive x axis & a unit vector j defined to point in the direction of the positive y axis: U = Ux i + U y j (2. 7) where Ux & Uy are scalar components of U ◦ Magnitude of U is given in terms of its components by the Pythagorean theorem: (2. 8) (C) 2005 Pearson Education South Asia Pte Ltd 19

2. 3 Components in 2 Dimensions Manipulating Vectors in Terms of Components: ◦ Sum of 2 vectors U & V: U + V = (Uxi + Uyj) + (Vxi + Vyj) = (Ux + Vx)i + (Uy + Vy)j ◦ Graphically: (2. 9) (C) 2005 Pearson Education South Asia Pte Ltd 20

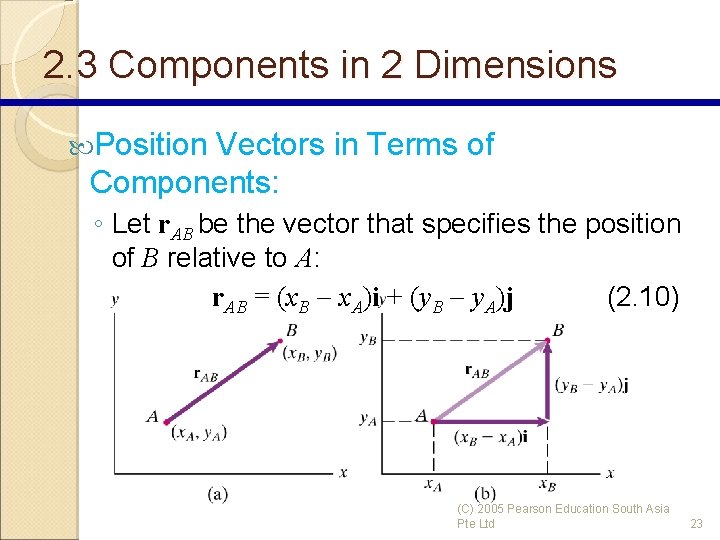
2. 3 Components in 2 Dimensions Position Vectors in Terms of Components: ◦ Consider point A with coordinates (x. A, y. A) & point B with coordinates (x. B, y. B) (C) 2005 Pearson Education South Asia Pte Ltd 22

2. 3 Components in 2 Dimensions Position Vectors in Terms of Components: ◦ Let r. AB be the vector that specifies the position of B relative to A: r. AB = (x. B x. A)i + (y. B y. A)j (2. 10) (C) 2005 Pearson Education South Asia Pte Ltd 23

Example 2. 2 Adding Vectors in Terms of Components The forces acting on the sailplane in Fig. 2. 15 are its weight W = 3500 j (N), the drag D = 1000 i + 500 j (N) & the lift L. Fig. 2. 15 (a) If the sum of the forces on the sailplane is zero, what are the components of L? (b) If the lift L has the components determined in (a) & the drag D increased by a factor of 2, what is the magnitude of the sum of the forces on the sailplane? (C) 2005 Pearson Education South Asia Pte Ltd 24

Example 2. 2 Adding Vectors in Terms of Components Strategy (a) By letting the sum of the forces = 0, we can determine the components of L. (b) Using the value of L from (a), we can determine the components of the sum of the forces & use Eq. (2. 8) to determine its magnitude. (C) 2005 Pearson Education South Asia Pte Ltd 25

Example 2. 2 Adding Vectors in Terms of Components Solution (a) Set the sum of forces = 0 with the forces expressed in N: W+D+L=0 (-3000 j) + ( 1000 i + 500 j) + L = 0 Solving for the lift, we obtain: L = 1000 i + 2500 j (N) (C) 2005 Pearson Education South Asia Pte Ltd 26

Example 2. 2 Adding Vectors in Terms of Components Solution (b) If the drag increases by a factor of 2, the sum of the forces on the sailplane: W From Eq. (2. 8), the magnitude of the sum is: (C) 2005 Pearson Education South Asia Pte Ltd 27

Example 2. 3 Determining Components in Terms of an Angle Hydraulic cylinders are used to exert forces in many mechanical devices. The force is exerted by the pressurized liquid (hydraulic fluid) pushing against a piston within the cylinder. The hydraulic cylinder AB in Fig. 2. 16 exerts 20, 000 -N force F on the bed of the dump truck at B. Express F in terms of components using the coordinate system shown. Fig. 2. 16 (C) 2005 Pearson Education South Asia Pte Ltd 28

Example 2. 3 Determining Components in Terms of an Angle Strategy When the direction of a vector is specified by an angle, we can determine the values of the components from the right triangle formed by the vector & its components. Solution Draw the vector F & its components: (C) 2005 Pearson Education South Asia Pte Ltd 29

Example 2. 3 Determining Components in Terms of an Angle Solution Fy points in the positive y direction: The vector F, in terms of its components: F = Fx + Fy = 17300 i + 10000 j (N) The x component of F is 17, 300 N & the y component is 10, 000 N. (C) 2005 Pearson Education South Asia Pte Ltd 31

Example 2. 3 Determining Components in Terms of an Angle Critical Thinking n When you have determined the components of a given vector, make sure they appear reasonable: Ø In this example, the x component should be negative & the y component positive n Make sure that the components yields the correct magnitude: (C) 2005 Pearson Education South Asia Pte Ltd 32

Example 2. 4 Determining Components The cable from point A to point B exerts 800 -N force F on the top of the television transmission tower in Fig. 2. 17. Express F in terms of components using the coordinate system shown. Fig. 2. 17 (C) 2005 Pearson Education South Asia Pte Ltd 33

Example 2. 4 Determining Components Strategy 1 st Method: ◦ Determine the angle between F & the y axis ◦ Determine the components from the right triangles formed by the vector F & its components 2 nd Method: ◦ The right triangles formed by F & its components are similar to triangle OAB ◦ Determine the components of F by using the ratios of the sides of these similar triangles (C) 2005 Pearson Education South Asia Pte Ltd 34

Example 2. 4 Determining Components Strategy 3 rd Method: ◦ Determine the components of the position vector r. AB from point A to point B ◦ Divide this vector by its magnitude, we obtain a unit vector e. AB with the same direction as F ◦ Obtain F in terms of its components by expressing it as the product of its magnitude & e. AB (C) 2005 Pearson Education South Asia Pte Ltd 35

Example 2. 4 Determining Components Solution n 1 st Method: From the right triangles formed by F & its vector components, the magnitude of Fx is: Magnitude of Fy is: (C) 2005 Pearson Education South Asia Pte Ltd 37

Example 2. 4 Determining Components Solution n 1 st Method: Since Fx points in the positive x direction & Fy points in the negative y direction: F = 358 i 716 j (N) (C) 2005 Pearson Education South Asia Pte Ltd 38

Example 2. 4 Determining Components Solution 2 nd Method: Length of cable AB: Since triangle OAB is similar to the triangle formed by F & its vector components: (C) 2005 Pearson Education South Asia Pte Ltd 39

Example 2. 4 Determining Components Solution n 3 rd Method: Divide this vector by its magnitude to obtain a unit vector e. AB that has the same direction as the force F: (C) 2005 Pearson Education South Asia Pte Ltd 43

Example 2. 4 Determining Components Critical Thinking To specify a vector, the magnitude & direction must be prescribed: ◦ In this example, the |F| is given ◦ The 40 -m & 80 -m dimensions in Fig. 2. 17 define the direction of the cable from A to B, which also defines the direction of F 1 st Method: ◦ Knowing the 40 -m & 80 -m dimensions determine the angle between the vertical & line AB ◦ |F| & was then used to calculate the components of F (C) 2005 Pearson Education South Asia Pte Ltd 45

Example 2. 4 Determining Components Critical Thinking 2 nd Method: ◦ Take advantage of the similar triangles ◦ Knowing |F| & the 40 -m & 80 -m dimensions F components 3 rd Method: ◦ Knowing the 40 -m & 80 -m dimensions express position vector from A to B in terms of its components ◦ Dividing that position vector by its magnitude unit vector with the same direction as F ◦ Multiply the unit vector by |F| F components (C) 2005 Pearson Education South Asia Pte Ltd 46

Example 2. 5 Determining an unknown Vector Magnitude The cables A & B in Fig. 2. 18 exert forces FA & FB on the hook. The magnitude of FA is 100 N. The tension in cable B has been adjusted so that the total force FA + FB is perpendicular to the wall to which the hook is attached. Fig. 2. 18 (a) What is the magnitude of FB? (b) What is the total force exerted on the hook by the 2 cables? (C) 2005 Pearson Education South Asia Pte Ltd 47

Example 2. 5 Determining an unknown Vector Magnitude Strategy The vector sum of the 2 forces is perpendicular to the wall, so the sum of the components parallel to the wall equals zero. From this condition we can obtain an equation for the magnitude of FB. Solution (a) Components of FA & FB are: (C) 2005 Pearson Education South Asia Pte Ltd 48

Example 2. 5 Determining an unknown Vector Magnitude Solution (a) Total force: Set the component of the total force parallel to the wall (the y component) = 0: Thus: (C) 2005 Pearson Education South Asia Pte Ltd 49

Example 2. 5 Determining an unknown Vector Magnitude Solution (b) With |FB|, the total force acting on the hook: The magnitude of the total force is 92. 2 N. (C) 2005 Pearson Education South Asia Pte Ltd 50

Example 2. 5 Determining an unknown Vector Magnitude Critical Thinking We can obtain the solution to (a) in a less formal way: ◦ If the component of the total force parallel to the wall is zero, the magnitude of the vertical component of FA must equal the magnitude of the vertical component of FB (C) 2005 Pearson Education South Asia Pte Ltd 51