Engineering Mechanics Friction in Action What is friction

Engineering Mechanics Friction in Action

What is friction? Friction is a retarding force that opposes motion. Friction types: Dry or Coulombic friction Sources of dry friction Static friction Kinetic friction Fluid friction Asperities between contacting surfaces Interactions at the atomic level Tribology studies sources of friction, lubrication, wear and tear etc.

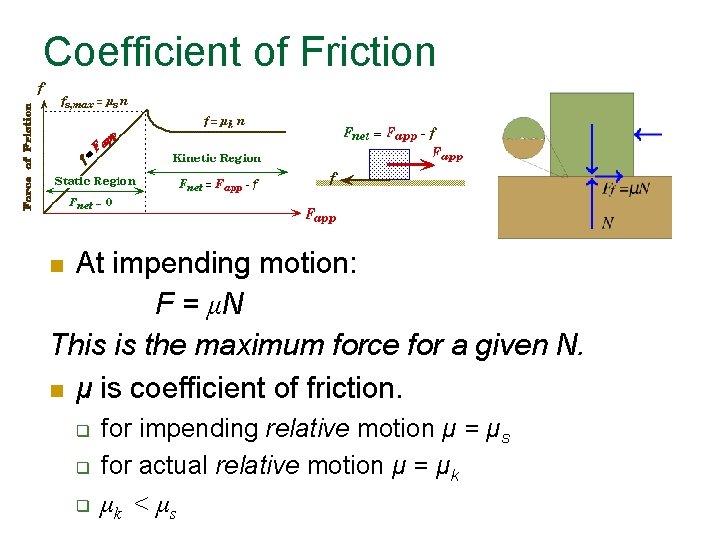
Coefficient of Friction At impending motion: F = μN This is the maximum force for a given N. μ is coefficient of friction. for impending relative motion μ = μs for actual relative motion μ = μk μk < μs

The Laws of Dry Friction. Coefficients of Friction • Maximum static-friction force: • Kinetic-friction force: • Maximum static-friction force and kineticfriction force are: - proportional to normal force - dependent on type and condition of contact surfaces - independent of contact area

The Laws of Dry Friction. Coefficients of Friction • Four situations can occur when a rigid body is in contact with a horizontal surface: • No friction, (Px = 0) • No motion, (Px < Fm) • Motion impending, (Px = Fm) • Motion, (Px > Fm)

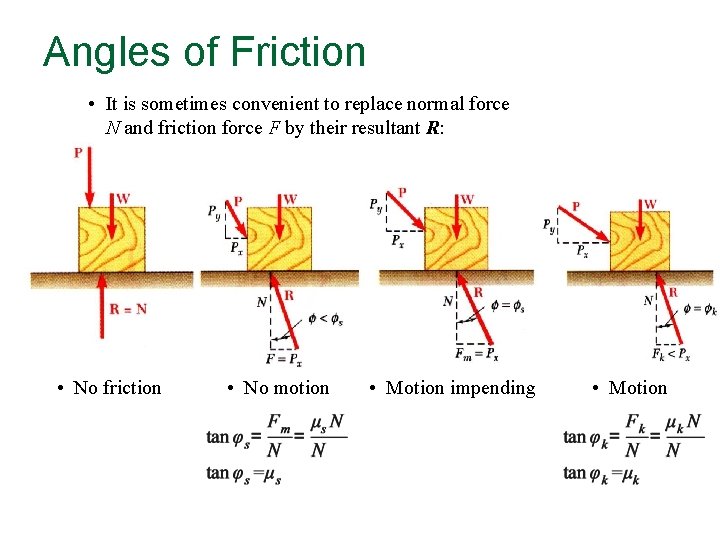
Angles of Friction • It is sometimes convenient to replace normal force N and friction force F by their resultant R: • No friction • No motion • Motion impending • Motion

Lighter Side of Friction

Friction is not always inanimate!

How to invoke laws of friction? Key: Always keep track of the number of unknowns and the number of equilibrium equation. Read : Beer and Johnston 8 th Ed. pgs 441442 Problem type 1: Like a usual equilibrium problem Solve using what we learnt earlier Only a couple of changes: Verify if the surface is capable of handling the load OR Find the minimum friction coefficient required. OR Given slipping occurs find the friction coefficient. Friction law need to be used at the very end.

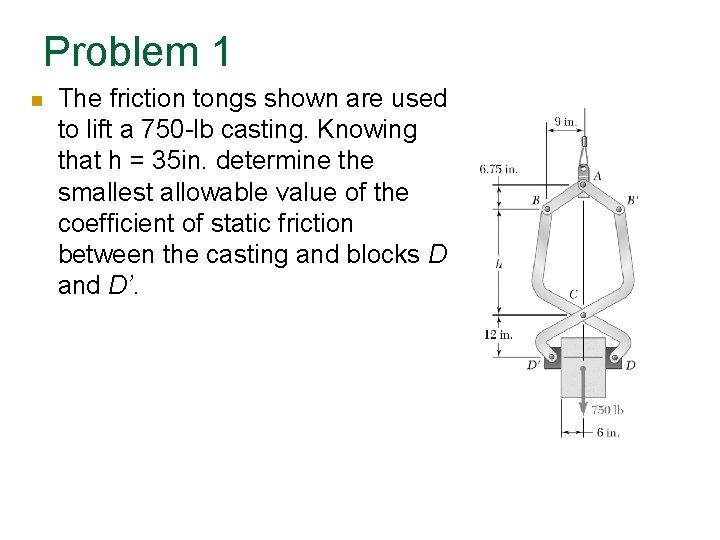
Problem 1 The friction tongs shown are used to lift a 750 -lb casting. Knowing that h = 35 in. determine the smallest allowable value of the coefficient of static friction between the casting and blocks D and D’.

Problem 2 A woman pedals her bicycle up a 5 -percent grade and a slippery road at a steady speed. The woman and bicycle have a combined mass of 82 kg. with mass center at G. If the rear wheel is on the verge of slipping, determine the coefficient of friction μs between the rear tire and the road. If the coefficient of friction is doubled, what would be the friction force acting on the rear wheel? (why may we neglect friction under the front wheel)

Problem 3 The light bar is used to support the 50 -kg block in its vertical guides. If the coefficient of static friction is 0. 3 at the upper end of the bar and 0. 4 at the lower end of the bar, find the friction force acting on each end for x = 75 mm. Also find the maximum value of x for which the bar will not slip.

Problem Type 2 Number of equations is less than number of unknowns. Motion of the body is impending. You are asked to obtain: Force/Torque required to start the impending motion. Some distance, angle etc. for the impending motion. Need to use the law of friction at impending surface. Careful about the sign of forces.

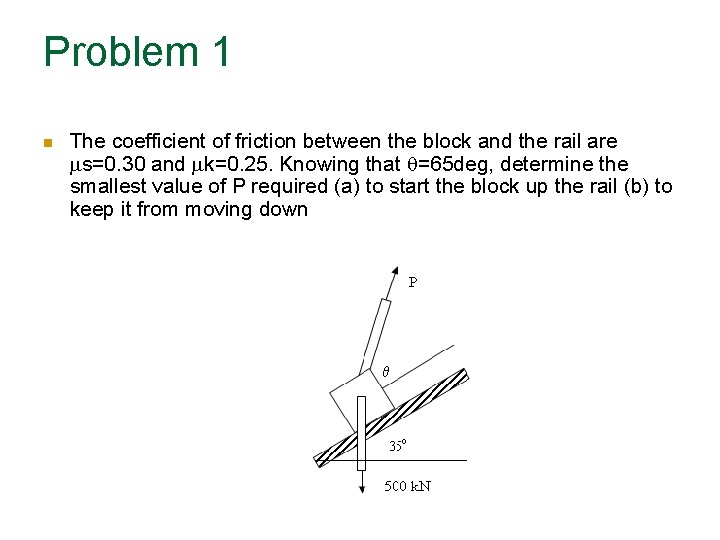
Problem 1 The coefficient of friction between the block and the rail are s=0. 30 and k=0. 25. Knowing that =65 deg, determine the smallest value of P required (a) to start the block up the rail (b) to keep it from moving down

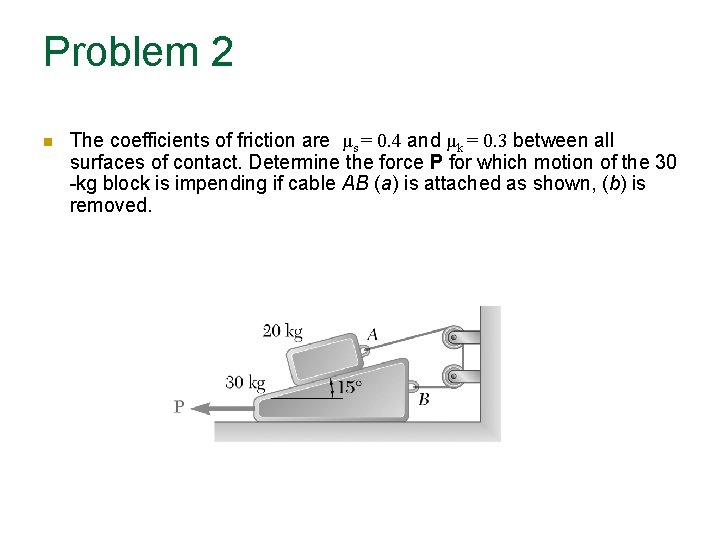
Problem 2 The coefficients of friction are μs = 0. 4 and μk = 0. 3 between all surfaces of contact. Determine the force P for which motion of the 30 -kg block is impending if cable AB (a) is attached as shown, (b) is removed.

Problem Type 3 Similar to Problem Type 2, but with one significant difference There can be multiple modes of slipping. Which particular contact at which the impending slippage occurs have to be decided by Trial and error Inspection Physical intuition. Ultimately it must be checked that everything is consistent, i. e. , the force on surfaces other than slipping surfaces should be less than μN. Caution: Be careful about the sign of forces

Problem 1 A block of mass mo is placed between the vertical wall and the small ideal roller at the upper end A of the uniform slender bar of mass m. The lower end B of the bar rests on the horizontal surface. If the coefficient of static friction is μs at B and also between the block and the wall, determine a general expression for the minimum value θmin of θ for which the block will remain in equilibrium. Evaluate the expression for μs = 0. 5 and m/mo = 10. For these conditions, check for possible slipping at B.

Problem 2 The 12 -lb slender rod AB is pinned at A and rests on the 36 -lb cylinder C. Knowing that the diameter of the cylinder is 12. 5 in. and that the coefficient of static friction is 0. 35 between all surfaces of contact, determine the largest magnitude of the force P for which equilibrium is maintained

Problem Type 4 Whethere is an impending slipping or sliding. If slipping occurs: F = μN at the point of slipping If tipping occurs Reactions at all points other than the point of tipping is equal to zero. Note that this case is just a special case of what we have seen earlier.

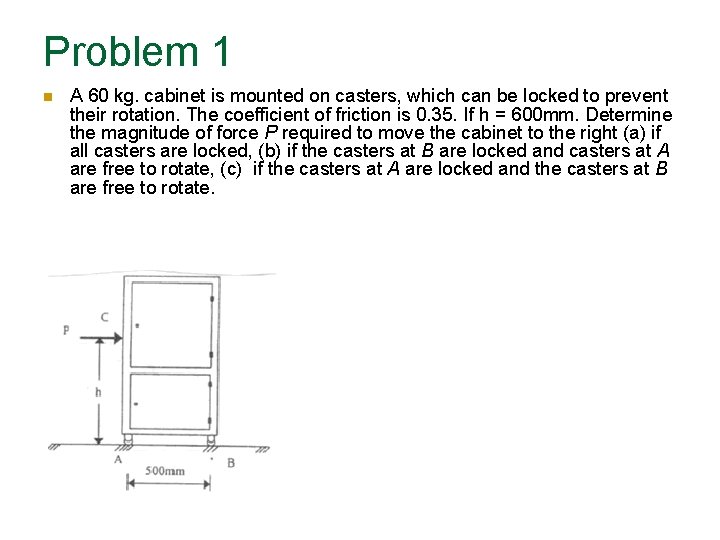
Problem 1 A 60 kg. cabinet is mounted on casters, which can be locked to prevent their rotation. The coefficient of friction is 0. 35. If h = 600 mm. Determine the magnitude of force P required to move the cabinet to the right (a) if all casters are locked, (b) if the casters at B are locked and casters at A are free to rotate, (c) if the casters at A are locked and the casters at B are free to rotate.

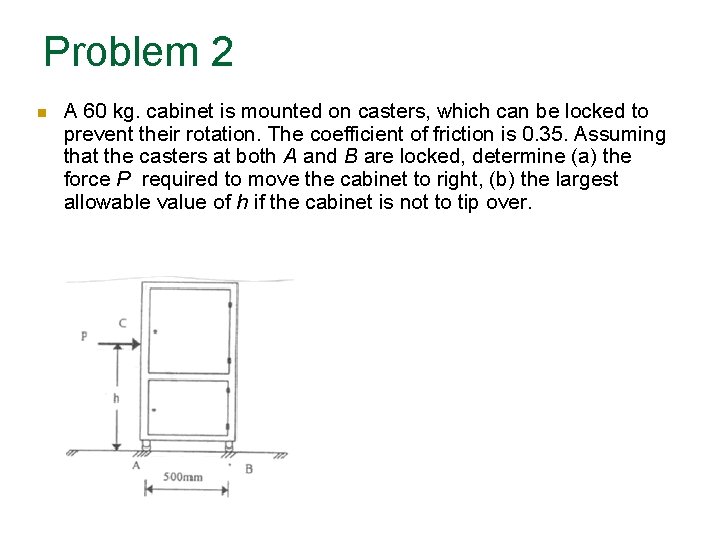
Problem 2 A 60 kg. cabinet is mounted on casters, which can be locked to prevent their rotation. The coefficient of friction is 0. 35. Assuming that the casters at both A and B are locked, determine (a) the force P required to move the cabinet to right, (b) the largest allowable value of h if the cabinet is not to tip over.

Extra Problem-1 Two slender rods of negligible weight are pinconnected at A and attached to the 18 -lb block B and the 80 -lb block C as shown. The coefficient of static friction is 0. 55 between all surfaces of contact. Determine the range of values of P for which equilibrium is maintained

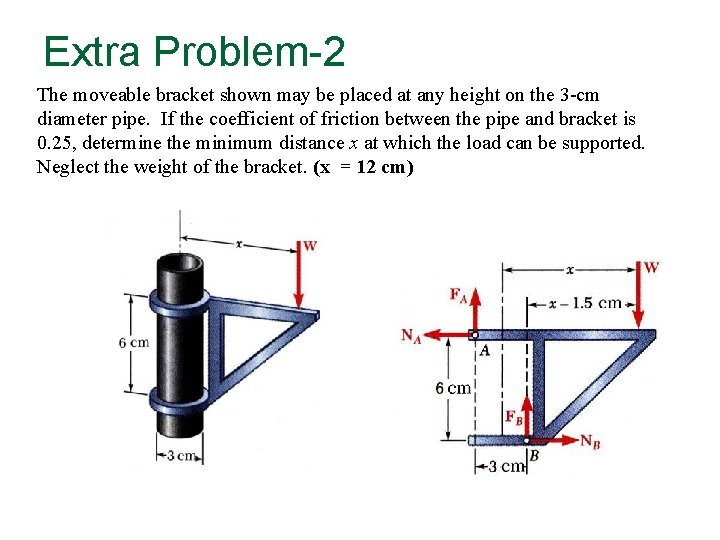
Extra Problem-2 The moveable bracket shown may be placed at any height on the 3 -cm diameter pipe. If the coefficient of friction between the pipe and bracket is 0. 25, determine the minimum distance x at which the load can be supported. Neglect the weight of the bracket. (x = 12 cm)

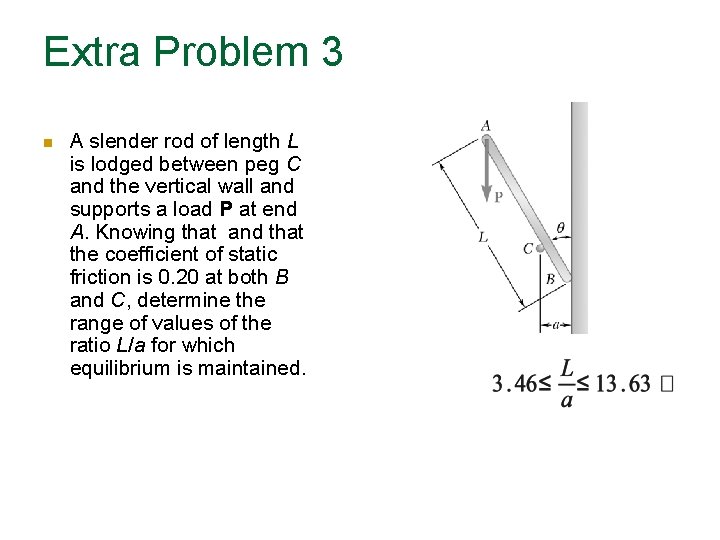
Extra Problem 3 A slender rod of length L is lodged between peg C and the vertical wall and supports a load P at end A. Knowing that and that the coefficient of static friction is 0. 20 at both B and C, determine the range of values of the ratio L/a for which equilibrium is maintained.

Extra Problem 4 Three flat blocks are positioned on the 30 deg. Incline as shown, and a force P parallel to the incline is applied to the middle block. The upper block is prevented moving by a wire which attached it to the fixed support. The coefficient of static friction for each of the three pairs of mating surfaces is shown. Determine the maximum value which P may have before any slipping takes place.

Note of caution: • The tips and classification of the problems done earlier is only a thumb rule. • Some problems may not fit into any category. • In any case such problems can be dealt with using ides discussed earlier. • Key is to always keep the track of the number of equations and the number of unknowns. • To check whether static friction, or kinetic friction is working look at the possible relative velocity between contacting surfaces.

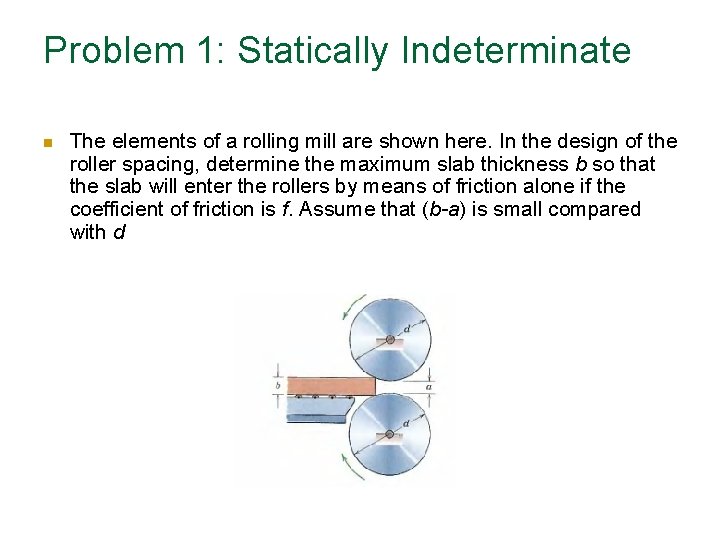
Problem 1: Statically Indeterminate The elements of a rolling mill are shown here. In the design of the roller spacing, determine the maximum slab thickness b so that the slab will enter the rollers by means of friction alone if the coefficient of friction is f. Assume that (b-a) is small compared with d

Belt Friction Used in many applications: Rotating pulleys transmit torques Band brakes Raising and lowering loads Use less smaller force to hold loads

Belt Friction Application capstan Diesel engine motor belt Band Brake

Belt Friction • Relate T 1 and T 2 when belt is about to slide to right. • Draw free-body diagram for element of belt • Combine to eliminate N, divide through by , • In the limit as goes to zero, • Separate variables and integrate from

Problem 2 Knowing that the coefficient of static friction is 0. 25 between the rope and the horizontal pipe and 0. 20 between the rope and the vertical pipe, determine the range of values of P for which equilibrium is maintained. Knowing that the coefficient of static friction is 0. 3 between the rope and the horizontal pipe and that the smallest value of P for which equilibrium is maintained is 20 N, determine (a) the largest value of P for which the equilibrium is maintained, (b) the coefficient of static friction between the rope and the vertical pipe

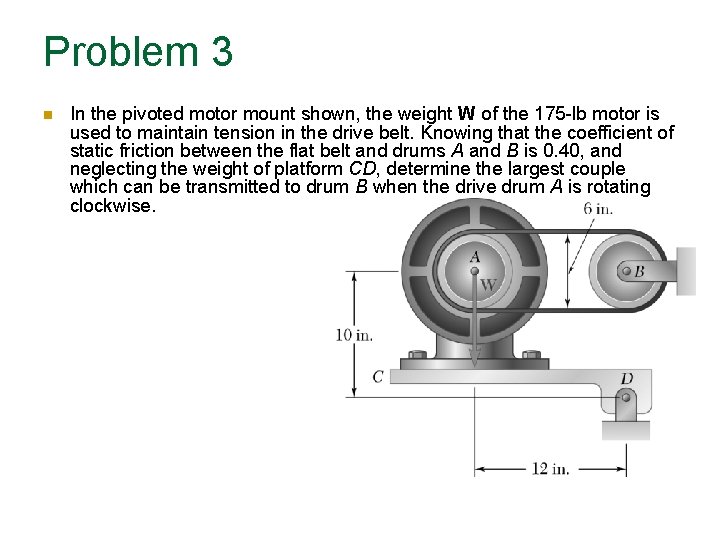
Problem 3 In the pivoted motor mount shown, the weight W of the 175 -lb motor is used to maintain tension in the drive belt. Knowing that the coefficient of static friction between the flat belt and drums A and B is 0. 40, and neglecting the weight of platform CD, determine the largest couple which can be transmitted to drum B when the drive drum A is rotating clockwise.

Problem 4 A flat belt connects pulley A to pulley B. The coefficients of friction are s = 0. 25 and k = 0. 20 between both pulleys and the belt. Knowing that the maximum allowable tension in the belt is 600 N, determine the largest torque which can be exerted by the belt on pulley A.

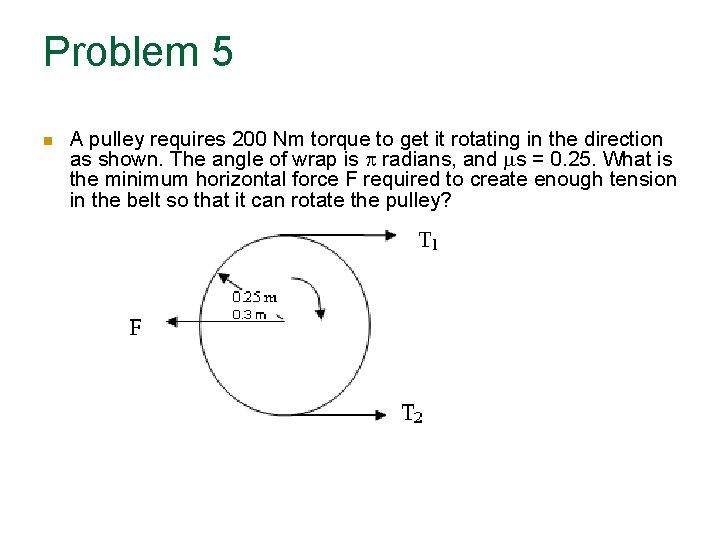
Problem 5 A pulley requires 200 Nm torque to get it rotating in the direction as shown. The angle of wrap is radians, and s = 0. 25. What is the minimum horizontal force F required to create enough tension in the belt so that it can rotate the pulley?

Extra Problem -1 A light flexible cord DABC is passed around the circular disk of mass m and ends in a small mass-less, frictionless pulley at C that is free to find its equilibrium position on the cord. The coefficient of friction between the cord and the disk is μ = 0. 5. Show that, for the position where the disk is on the verge of turning under the action of a couple M applied to the disk, the angle (BOA) between the normals (OB and OA) to the cord at the tangency points (B and A) is equal to α = 87. 3 o.

Extra Problem 2 A conveyer is moving ten 50 lb boxes at a constant speed at a 45 deg. setting. The dynamic coefficient of friction between the belt and the bed of the conveyer is 0. 05. Furthermore, the static coefficient of friction between the drivingpulley and the belt is 0. 4. The idler pulley is moved along the direction of the conveyor by a crank mechanism so that the idler puley is subject to a force F of 500 lb. Compute the maximum tension found in the belt and ascertain if there will be slipping on the driving pulley. Neglect weight of the belt.

Tutorial: Problem 1 What is the maximum possible height h of the step shown in the figure so that some force P will roll the 25 kg cylinder over the step? Take coefficient of static friction to be equal to 0. 3.

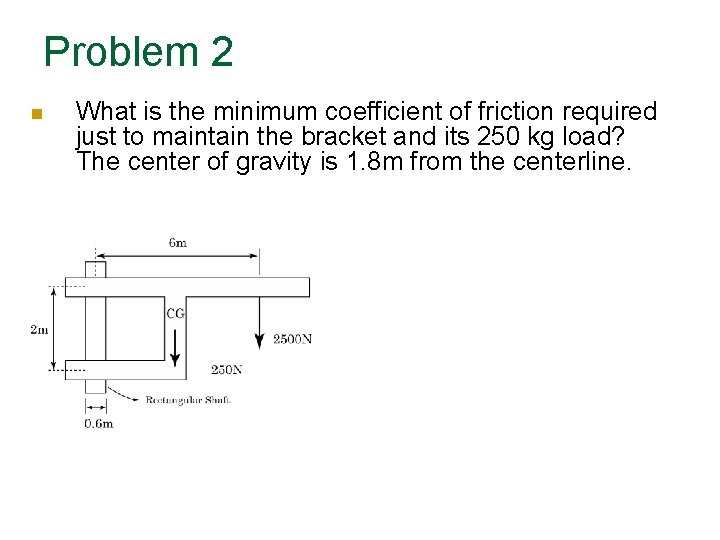
Problem 2 What is the minimum coefficient of friction required just to maintain the bracket and its 250 kg load? The center of gravity is 1. 8 m from the centerline.

Problem 3 What is the force F to hold two cylinders, each having a mass of 50 kg? Take the coefficient of friction equal to 0. 2 for all surfaces of contact.

Problem 4 A light metal panel is welded to two short sleeves of 0. 025 m inside diameter that can slide on a fixed horizontal rod. The coefficient of friction between the sleeves and the rod are μs = 0. 4 and μk = 0. 3. A cord attached to corner C is used to move the panel along the rod. Knowing that the cord lies in the same vertical plane as the panel, determine the range of values of θ for which the panel will be in impending motion to the right.

Problem 5 The uniform slender bar of length l is placed in the opening of width d at the 30 o angle shown. For what range of l/d will the bar remain in static equilibrium? The coefficient of static friction at A and B is μs = 0. 4

Complex Friction Point friction: Impending motion is same for all points Complex friction: The relative motion is different for each point This leads to a difference in the method of analysis

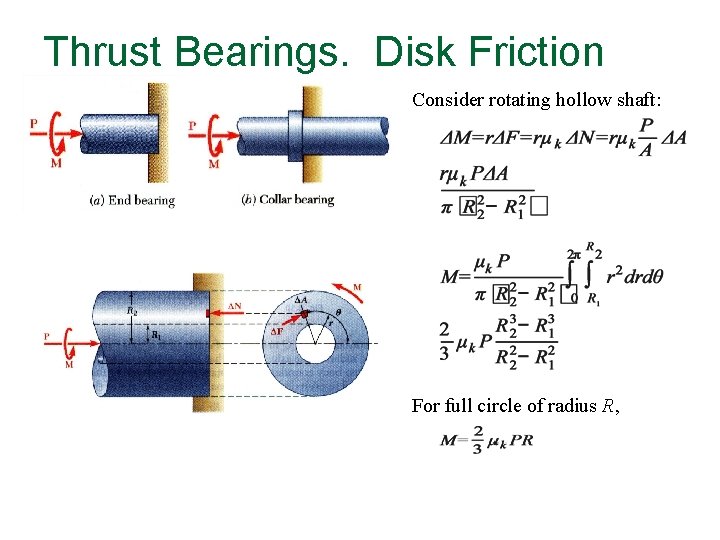
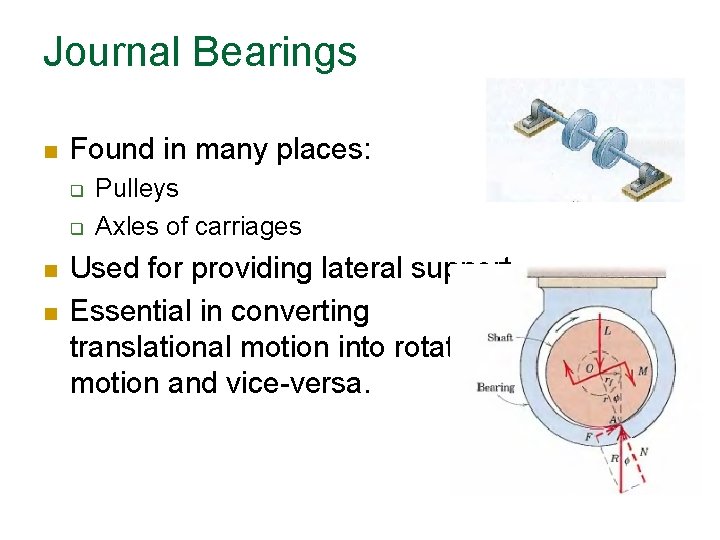
Bearings A bearing is a device to allow constrained rotational or translational relative motion between two parts. Different types of bearing: Thrust bearing Disc friction Journal bearing Ball bearing for earthquake-proof building Most applications in mechanical systems

Disc Friction Between two circular surfaces, or between circular and a flat surface. There is an thrust load between the two surfaces. Example: Clutch plates Sanding machine Disc brakes demonstrations at: http: //www. howstuffworks. com/bearing. htm

Thrust Bearings. Disk Friction Consider rotating hollow shaft: For full circle of radius R,

Journal Bearings Found in many places: Pulleys Axles of carriages Used for providing lateral support. Essential in converting translational motion into rotational motion and vice-versa.

Belt Friction Used in many applications: Rotating pulleys transmit torques Band brakes Raising and lowering loads Use less smaller force to hold loads

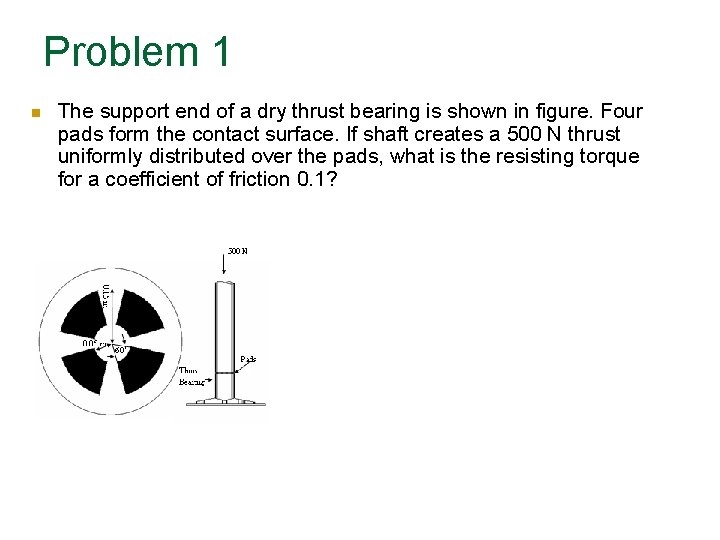
Problem 1 The support end of a dry thrust bearing is shown in figure. Four pads form the contact surface. If shaft creates a 500 N thrust uniformly distributed over the pads, what is the resisting torque for a coefficient of friction 0. 1?

Problem 6 Replace the flat belt and pulley discussed in the class by a V-belt and matching grooved pulley as indicated by the cross-sectional view shown in the figure. Derive the relation among the belt tensions, the angle of contact, and the coefficient of friction for the V-belt when slipping impends. A V-belt design with α = 35 deg would be equivalent to increasing the coefficient of friction for a flat belt of the same material by what factor n?

Tutorial Problem 1 Compute the frictional torque needed to rotate truncated cone relative to the cone has a 0. 05 m diameter base and 600 cone angle, and it is cut off 0. 075 m from the cone tip. The coefficient of dynamic friction is 0. 2.

Problem 2 A cord is wiped twice around a caption A and three times around second caption B. Finally cord goes over a half barrel section and supports a mass M of 500 kg. What is tension T required to maintain this load? Take coefficient of friction 0. 1 for all surfaces of contact.

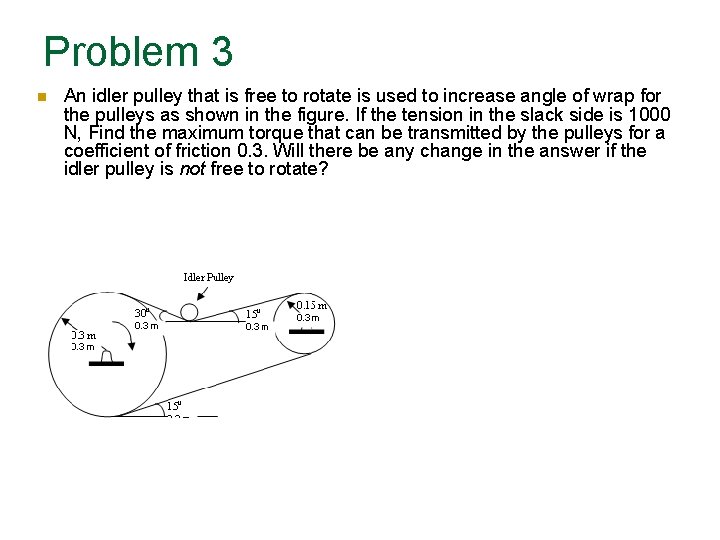
Problem 3 An idler pulley that is free to rotate is used to increase angle of wrap for the pulleys as shown in the figure. If the tension in the slack side is 1000 N, Find the maximum torque that can be transmitted by the pulleys for a coefficient of friction 0. 3. Will there be any change in the answer if the idler pulley is not free to rotate?

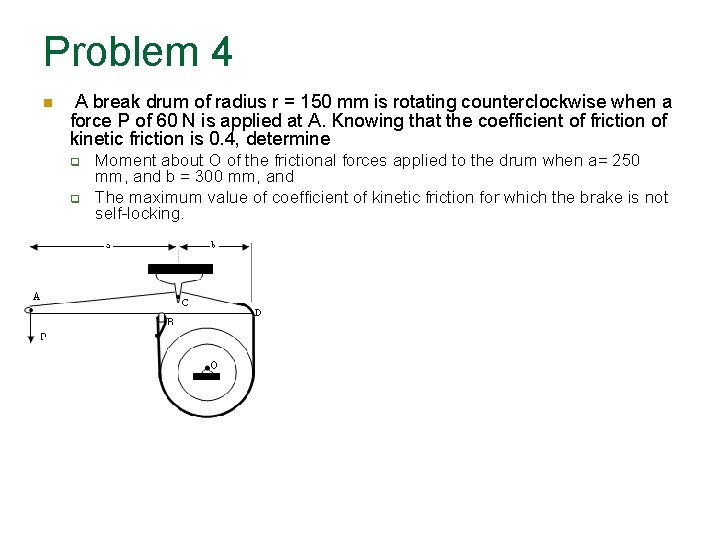
Problem 4 A break drum of radius r = 150 mm is rotating counterclockwise when a force P of 60 N is applied at A. Knowing that the coefficient of friction of kinetic friction is 0. 4, determine Moment about O of the frictional forces applied to the drum when a= 250 mm, and b = 300 mm, and The maximum value of coefficient of kinetic friction for which the brake is not self-locking.