Engineering Mechanics Dynamics in SI Units 12 e










































- Slides: 47

Engineering Mechanics: Dynamics in SI Units, 12 e Vibrations Dr. Voon Chun Hong Copyright © 2010 Pearson Education South Asia Pte Ltd

Chapter Objectives n n Discuss undamped one-degree-of-freedom vibration of a rigid body using the equation of motion and energy methods Study the analysis of undamped forced vibration and viscous damped forced vibration. Copyright © 2010 Pearson Education South Asia Pte Ltd

Chapter Outline 1. 2. 3. 4. 5. Undamped Free Vibration* Energy Methods* Undamped Forced Vibration* Viscous Damped Free Vibration* Viscous Damped Forced Vibration* Copyright © 2010 Pearson Education South Asia Pte Ltd

22. 1 Undamped Free Vibration* n n A vibration is a periodic motion of a body or system of connected bodies displaced from a position of equilibrium Free vibration occurs when the motion is maintained by gravitational or elastic restoring forces Forced vibration is caused by an external periodic or intermittent force applied to the system Both of these types of vibration may be either damped or undamped Copyright © 2010 Pearson Education South Asia Pte Ltd

22. 1 Undamped Free Vibration* n n Undamped vibrations can continue indefinitely as frictional effects are neglected The block has a mass m and is attached to a spring having a stiffness k Elastic restoring force F = kx is directed toward the equilibrium position Acceleration a is assumed to act in the direction of positive displacement Copyright © 2010 Pearson Education South Asia Pte Ltd

22. 1 Undamped Free Vibration* n We have n Acceleration is proportional to displacement Motion is called simple harmonic motion Rearranging, we get ωn is the natural frequency (rad/s), is homogeneous, second-order, linear, differential equation with constant coefficients, and the general solution is n n Copyright © 2010 Pearson Education South Asia Pte Ltd

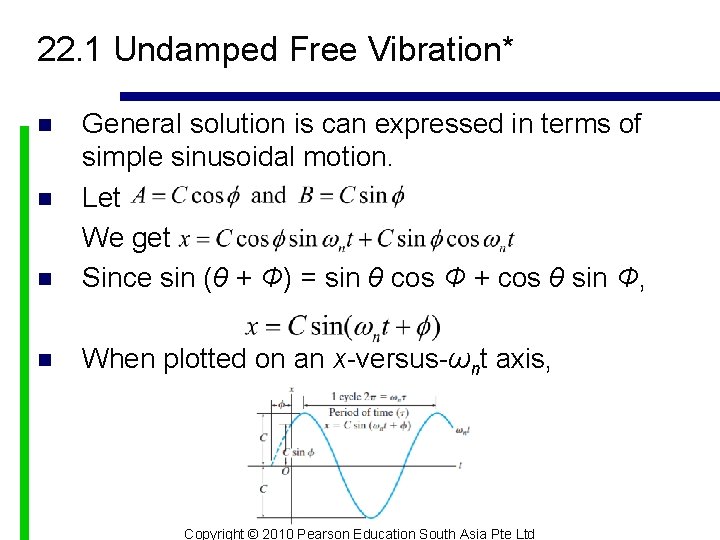
22. 1 Undamped Free Vibration* n General solution is can expressed in terms of simple sinusoidal motion. Let We get Since sin (θ + Φ) = sin θ cos Φ + cos θ sin Φ, n When plotted on an x-versus-ωnt axis, n n Copyright © 2010 Pearson Education South Asia Pte Ltd

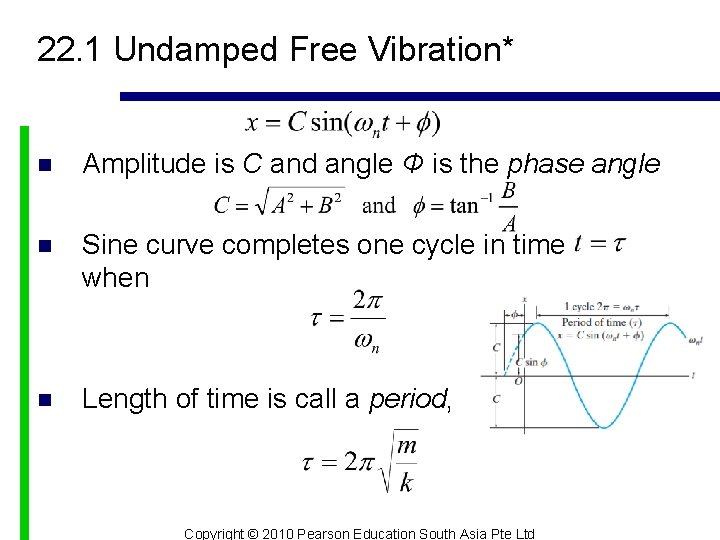
22. 1 Undamped Free Vibration* n Amplitude is C and angle Φ is the phase angle n Sine curve completes one cycle in time when n Length of time is call a period, Copyright © 2010 Pearson Education South Asia Pte Ltd

22. 1 Undamped Free Vibration* n Frequency f (hertz, Hz) is defined as the number of cycles completed per unit of time, n Body’s motion is described by a differential equation of the same “standard form” as Copyright © 2010 Pearson Education South Asia Pte Ltd

22. 1 Undamped Free Vibration* Procedures for Analysis Free-Body Diagram n Draw the FBD of the body when the body is displaced by a small amount from its equilibrium position. n Locate the body with respect to its equilibrium position by using an appropriate inertial coordinate q n a. G or the body’s angular acceleration α should have a sense of direction. Copyright © 2010 Pearson Education South Asia Pte Ltd

22. 1 Undamped Free Vibration* Procedures for Analysis Free-Body Diagram n If the rotational equation of motion ∑ MP = (Mk)P is to be used, then it may be beneficial to also draw the kinetic diagram since it graphically accounts for the components m(a. G)x, m(a. G)y, and I Gα Equation of Motion n Apply the equation to relate the elastic or gravitational restoring forces and couple moments acting on the body to the body’s accelerated motion. Copyright © 2010 Pearson Education South Asia Pte Ltd

22. 1 Undamped Free Vibration* Procedures for Analysis Kinematics n Express the body’s accelerated motion in terms of the second time derivative of the position coordinates. n Substitute the result into the equation of motion and determine ωn Copyright © 2010 Pearson Education South Asia Pte Ltd

Example 1 Determine the period of vibration for the simple pendulum shown. The bob has a mass m and is attached to a cord of length l. Copyright © 2010 Pearson Education South Asia Pte Ltd

Example 1 Solution Free-Body Diagram Motion of the system is related to the position θ. at acts in the direction of increasing s. Equation of Motion (1) Copyright © 2010 Pearson Education South Asia Pte Ltd

Example 1 Solution Kinematics We have s may be related to θ by the equation s = lθ, Eq. 1 reduces to For small displacements, sin θ ≈ θ, Comparing with , the period of time required is Copyright © 2010 Pearson Education South Asia Pte Ltd

Quiz Copyright © 2010 Pearson Education South Asia Pte Ltd

Quiz Answer Copyright © 2010 Pearson Education South Asia Pte Ltd

22. 2 Energy Methods* n n n Simple harmonic motion of a body is due only to gravitational and elastic restoring forces acting on the body These types of forces are said to be conservative When the block is displaced an arbitrary amount x from equilibrium position, the kinetic energy is T. 2 2 = ½ mv = ½ mx and the potential energy is V = ½ kx 2 Copyright © 2010 Pearson Education South Asia Pte Ltd

22. 2 Energy Methods* n By conservation of energy equation, n Differential equation describing the accelerated motion of the block can be obtained by Copyright © 2010 Pearson Education South Asia Pte Ltd

22. 2 Energy Methods* n Since the velocity x is not always zero in a vibrating system, n If the energy is written for a system of connected bodies, the natural frequency or the equation of motion can also be determined by time differentiation Copyright © 2010 Pearson Education South Asia Pte Ltd

22. 2 Energy Methods* Procedure for Analysis Energy Equation n Draw the body when it is displaced by a small amount from its equilibrium position n Formulate the equation of energy for the body, T + V = constant n Kinetic energy must account for T = ½ mv. G 2 + ½ IGωn 2 n The potential energy is V = Vg + Ve n Vg should be measured from a datum for which q =0 Copyright © 2010 Pearson Education South Asia Pte Ltd

22. 2 Energy Methods* Procedure for Analysis Time Derivatives n The resultant differential equation represents the equation of motion for the system n The value of ωn is obtained after rearranging the terms in the “standard form”, Copyright © 2010 Pearson Education South Asia Pte Ltd

Example 22. 5 The thin hoop is supported by a peg at O. Determine the natural period of oscillation for small amplitudes of swing. The hoop has a mass m. Copyright © 2010 Pearson Education South Asia Pte Ltd

Example 22. 5 Solution Energy Equation From formula and parallel-axis theorem, we determine IO by For small angles, potential energy is Copyright © 2010 Pearson Education South Asia Pte Ltd

Example 22. 5 Solution Energy Equation Total energy is the system is Time Derivative We have Since θ is not always equal to zero, Copyright © 2010 Pearson Education South Asia Pte Ltd

Example 22. 5 Solution Time Derivative Hence, So that, Copyright © 2010 Pearson Education South Asia Pte Ltd

22. 3 Undamped Forced Vibration* Periodic Force n The block and spring represents the vibrational characteristics of a system subjected to a periodic force F = F 0 sin ω0 t n This force has an amplitude of F 0 and a forcing frequency ω0 n Applying equation of motion, Copyright © 2010 Pearson Education South Asia Pte Ltd

22. 3 Undamped Forced Vibration* Periodic Force n Equation referred to as a non-homogeneous second-order differential equation n It consists of a complimentary solution, xc, plus a particular solution, xp n The complimentary solution is determined by setting right side to zero and solving results n Since the motion is periodic, Copyright © 2010 Pearson Education South Asia Pte Ltd

22. 3 Undamped Forced Vibration* Periodic Force n Taking the second time derivative and substituting into the differential equation, n Factoring out sin ωt and solving for C, Copyright © 2010 Pearson Education South Asia Pte Ltd

22. 3 Undamped Forced Vibration* Periodic Force n Therefore for particular solution n The general solution is Copyright © 2010 Pearson Education South Asia Pte Ltd

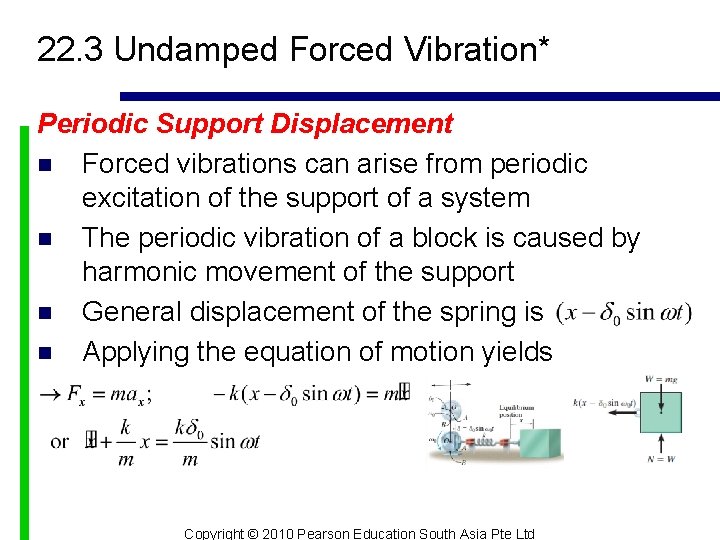
22. 3 Undamped Forced Vibration* Periodic Support Displacement n Forced vibrations can arise from periodic excitation of the support of a system n The periodic vibration of a block is caused by harmonic movement of the support n General displacement of the spring is n Applying the equation of motion yields Copyright © 2010 Pearson Education South Asia Pte Ltd

Example 22. 7 The instrument is rigidly attached to a platform P, which in turn is supported by four springs, each having a stiffness k = 800 N/m. If the floor is subjected to a vertical displacement = 10 sin (8 t) mm where t is in seconds, determine the amplitude of steady-state vibration. What is the frequency of the floor vibration required to cause resonance? The instrument and platform have a total mass of 20 kg. Copyright © 2010 Pearson Education South Asia Pte Ltd

Example 22. 7 Solution Since the induced vibration is caused by the displacement of the supports, (1) For mm, the natural frequency Copyright © 2010 Pearson Education South Asia Pte Ltd

Example 22. 7 Solution The amplitude of vibration is Resonance will occur when the amplitude of vibration X caused by the floor displacement approaches infinity. Thus Copyright © 2010 Pearson Education South Asia Pte Ltd

22. 4 Viscous Damped Free Vibration* n n n Damping is attributed to the resistance created by the substance, such as water, air, oil, or in which the system vibrates This type of force developed under these conditions is called a viscous damping force, Damping occurs when the piston P moves to the right or left within the enclosed cylinder Copyright © 2010 Pearson Education South Asia Pte Ltd

22. 4 Viscous Damped Free Vibration* n Applying the equation of motion yields n This linear, second-order, homogeneous, differential equation has solutions of form We can obtain two values of λ, n Copyright © 2010 Pearson Education South Asia Pte Ltd

22. 4 Viscous Damped Free Vibration* n The critical damping coefficient cc is Overdamped System n When c < cc, the roots λ 1 and λ 2 are both real n Motion corresponding to this solution is nonvibrating Copyright © 2010 Pearson Education South Asia Pte Ltd

22. 4 Viscous Damped Free Vibration* Critically Damped System n If c = cc, then λ 1 = λ 2 = - cc/2 m = ωn, we have Underdamped System n Cases where c < cc n The roots λ 1 and λ 2 are complex numbers and the general solution is Copyright © 2010 Pearson Education South Asia Pte Ltd

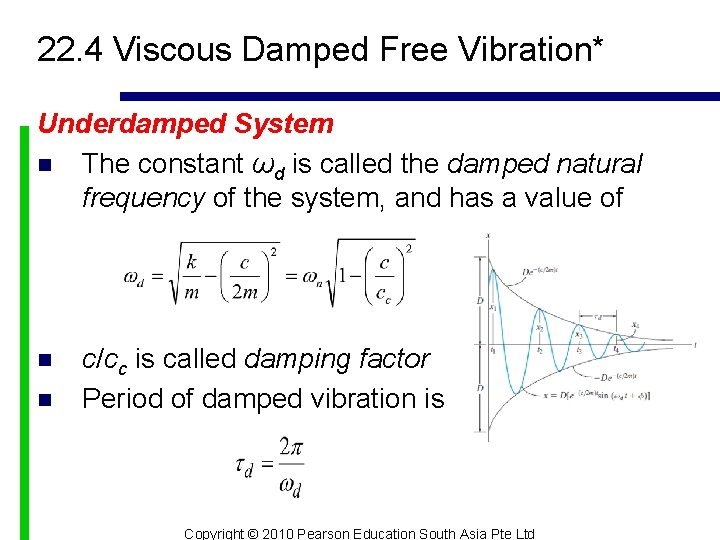
22. 4 Viscous Damped Free Vibration* Underdamped System n The constant ωd is called the damped natural frequency of the system, and has a value of n n c/cc is called damping factor Period of damped vibration is Copyright © 2010 Pearson Education South Asia Pte Ltd

22. 5 Viscous Damped Forced Vibration* n The differential equation which describes the motion is n Particular solution is n Solving for constant A’ and B’, Copyright © 2010 Pearson Education South Asia Pte Ltd

22. 5 Viscous Damped Forced Vibration* n It is also possible to express the particular solution in the form of where Copyright © 2010 Pearson Education South Asia Pte Ltd

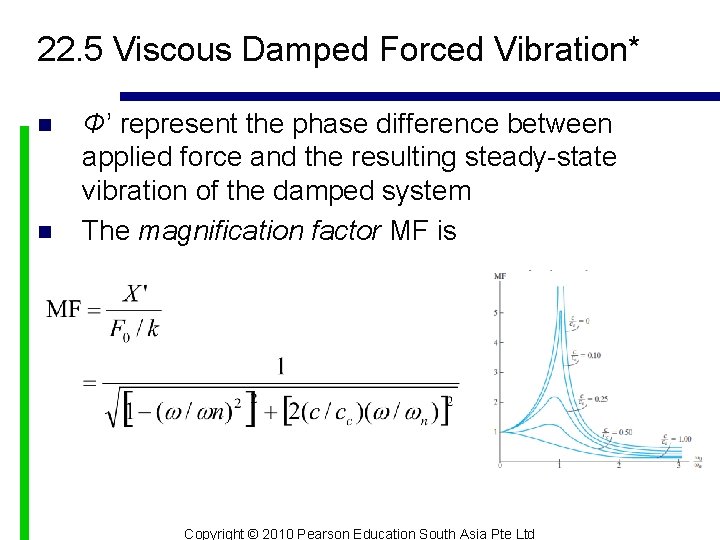
22. 5 Viscous Damped Forced Vibration* n n Φ’ represent the phase difference between applied force and the resulting steady-state vibration of the damped system The magnification factor MF is Copyright © 2010 Pearson Education South Asia Pte Ltd

Example 22. 8 The 30 -kg electric motor is supported by four springs, each having a stiffness of 200 N/m. if the rotor R is unbalanced such that its effect is equivalent to a 4 -kg mass located 60 mm from the axis of rotation, determine the amplitude of vibration when the rotor is turning at ω = 10 rad/s. The damping ratio is c/cc = 0. 15 Copyright © 2010 Pearson Education South Asia Pte Ltd

Example 22. 8 Solution Force has a constant magnitude of Since F = F 0 sin ωt, where ω = 10 rad/s, Stiffness of the entire system of 4 springs is k = 4(200) = 800 N/m Copyright © 2010 Pearson Education South Asia Pte Ltd

Example 22. 8 Solution Natural frequency of vibration is Since the damping factor is known, the steady-state amplitude is Copyright © 2010 Pearson Education South Asia Pte Ltd

Assignment n n Question 1 A 4 -kg block is suspended from a spring having a stiffness of 1600 N/m. If the block is given an upward velocity of 4 m/s when it is displaced downward a distance of 300 mm from its equilibrium position, 1. Determine the equation which describes the motion. 2. What is the amplitude of the motion? Assume that positive displacement is downward. Copyright © 2010 Pearson Education South Asia Pte Ltd

Assignment n n Question 2 If the lower end of the 12 -kg slender rod is displaced a small amount and released from rest, determine the natural frequency of vibration. Each spring has a stiffness of k = 400 N/m and is unstretched when the rod is hanging vertically. Copyright © 2010 Pearson Education South Asia Pte Ltd