Engineering Mechanics Centroid and Centre of Gravity CG

Engineering Mechanics Centroid and Centre of Gravity (CG) Prepared by, Dr. S. Elangovan Mr. N. Muthuram Department of Production Engineering PSG College of Technology Coimbatore - 641004 This work is licensed under the Creative Commons Attribution 4. 0 International License. To view a copy of this license, visit http: //creativecommons. org/licenses/by/4. 0/ or send a letter to Creative Commons, PO Box 1866, Mountain View, CA 94042, USA.

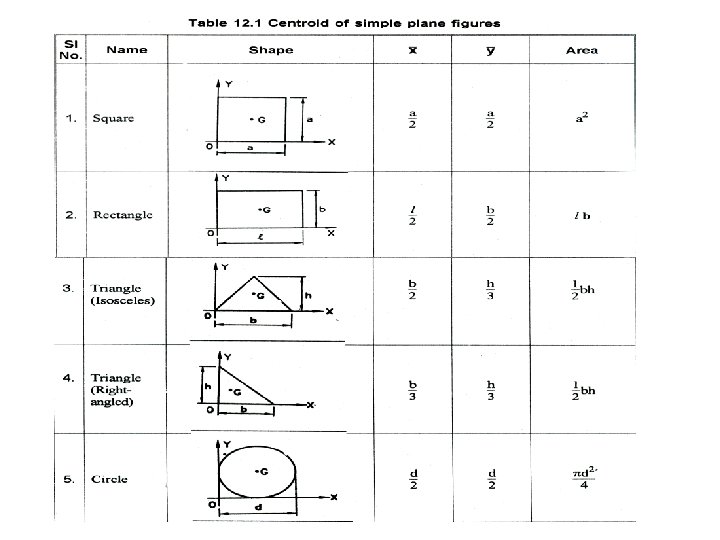
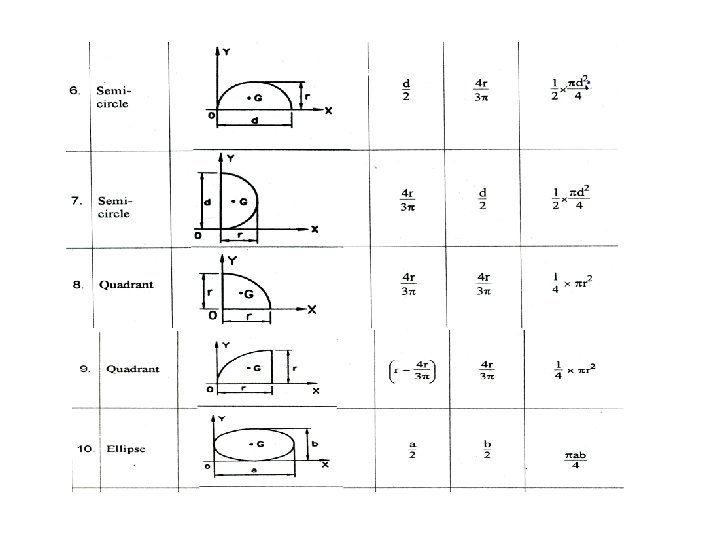
Centroid • It is a geometric centre of the body. • The point, at which the total area of a plane figure is assumed to be concentrated irrespective of the position of the plane figure. • Plane figure having area but no volume. • The centroid is a point where you could suspend a body with a string and the body would not have a tendency to rotate. • The symbol for the Centroid is • Example: Rectangle, Triangle, Square, Circle, Semicircle, Quadrilateral, etc. ,

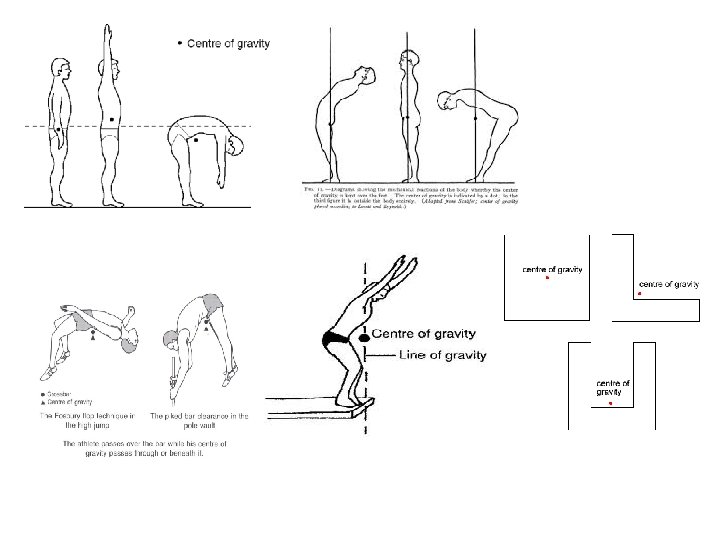
Real life application of Centroid v. Lots of construction applications and engineering applications to design things or structure so that minimal stress and energy is used stabilize a component v. In stress and deflection analysis of a beam, the location of centroid is very important

Centroid For areas that have symmetry around an axis, the centroid is located on that axis.

15 The centroid “C” of the Area segment, AREAS: when the density ρ, is constant and the body has a small constant thickness t, the body can be modeled as a surface area. The mass of an element becomes dm = ρ t d. A. If ρ and t are constant over entire area, the coordinates of the ‘centre of mass’ also becomes the coordinates of the centroid, C of the surface area and which may be written as

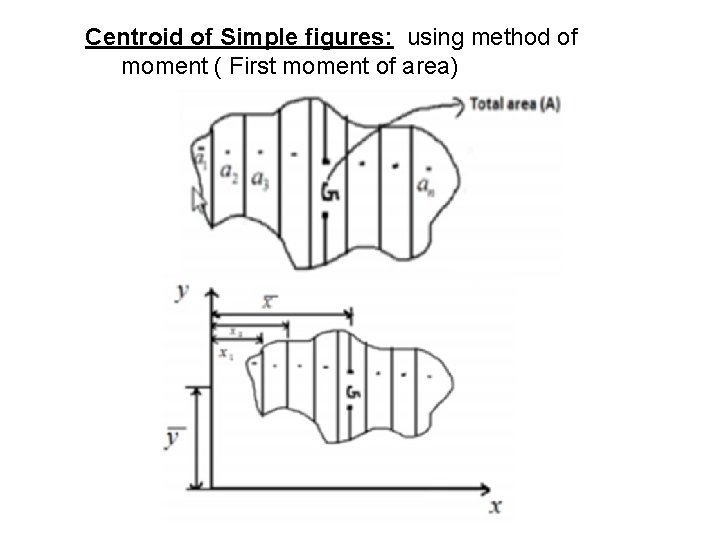
Centroid of Simple figures: using method of moment ( First moment of area)

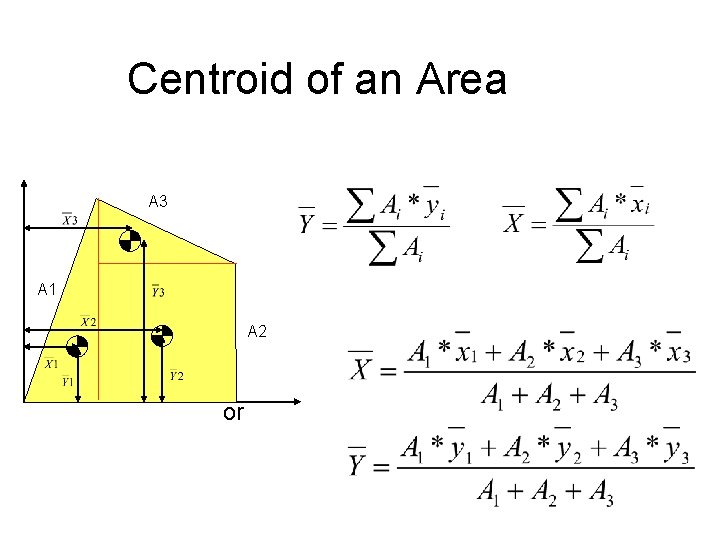
18 The coordinates of the centroid of the surface area about any axis can be calculated by using the eqn. (A) x = (a 1) x 1 + (a 2) x 2 + (a 3) x 3 + ………. +(an) xn = First moment of area Moment of Total area ‘A’ about y-axis = Algebraic Sum of moment of elemental ‘d. A’ about the same axis where (A = a 1 + a 2 + a 3 + a 4 + ……. . + an)

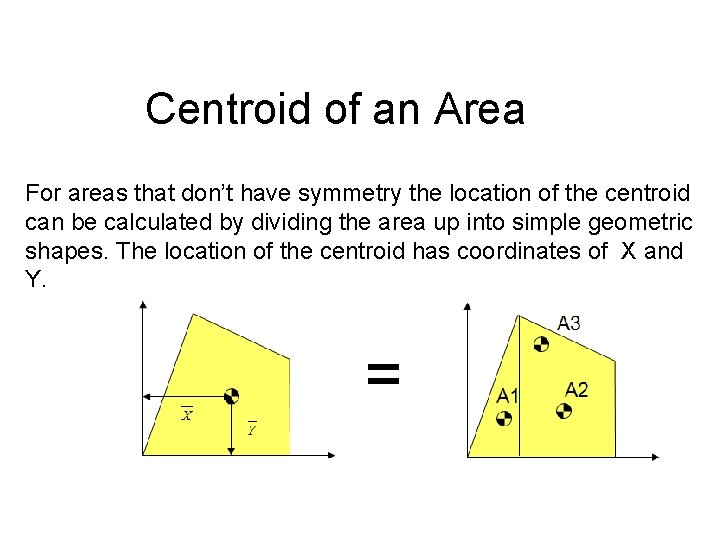
Centroid of an Area For areas that don’t have symmetry the location of the centroid can be calculated by dividing the area up into simple geometric shapes. The location of the centroid has coordinates of X and Y.

Centroid of an Area A 3 A 1 A 2 or

REFERENCE AXES AND CENTROIDAL AXES • REFERENCE AXES: The location of the centroid is always measured with reference to some reference axes. Generally two axes are used for the centroid of the plane figure. The horizontal reference axis (OX) is taken on the bottom edge of the figure and the vertical reference axis (OY) is taken on the left edge of the figure. • CENTROIDAL AXES: The axes which are passing through the centroid of the figure is called the centroidal axes. The horizontal and vertical axes passing through G, are XX and YY axis respectively.

Centre of Gravity (CG) • Centre of gravity is defined as the point through which the whole weight of the body acts (or) assumed to be concentrated. • When this is referred to weightless laminas or plane areas is called the centroid of the area. • A body is having only one center of gravity for all positions of the body. It may within the body or even outside the body • It is represented by CG. or simply G or C.

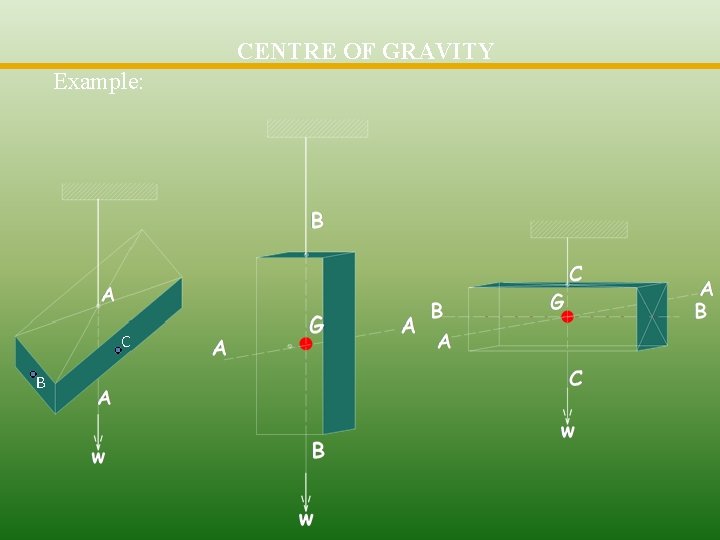
2 CENTRE OF GRAVITY Consider a three dimensional body of any size and shape, having a mass m. If we suspend the body as shown in figure, from any point such as A, the body will be in equilibrium under the action of the tension in the cord and the resultant W of the gravitational forces acting on all particles of the body.

4 CENTRE OF GRAVITY We repeat the experiment by suspending the body from other points such as B and C, and in each instant we mark the line of action of the resultant force. For all practical purposes these lines of action will be concurrent at a single point G, which is called the centre of gravity of the body.

CENTRE OF GRAVITY Example: C B

6 CENTRE OF GRAVITY To determine mathematically the location of the centre of gravity of any body, we apply the principle of moments to the parallel system of gravitational forces. Centre of gravity is that point about which the summation of the first moments of the weights of the elements of the body is zero.

CENTRE OF GRAVITY The moment of the resultant gravitational force W, about any axis 7 = the algebraic sum of the moments about the same axis of the gravitational forces d. W acting on all infinitesimal elements of the body. if, we apply principle of moments, (Varignon’s Theorem) about y-axis, for example, The moment of the resultant about y-axis = The sum of moments of its components about y-axis Where W =resultant gravitational force

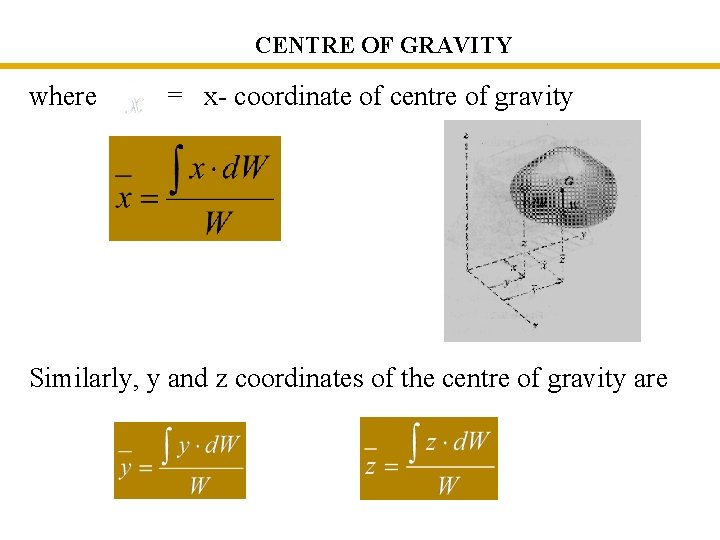
8 CENTRE OF GRAVITY where = x- coordinate of centre of gravity Similarly, y and z coordinates of the centre of gravity are and ----(1)

Difference between Centroid and Centre of Gravity (CG) Centroid • Centroid applies to plane areas • Centroid is the point in a plane area such that the moment of area about any axis through that point is zero Centre of Gravity • CG applies to the bodies with mass and weight • CG is the point through which the resultant gravitational force (weight) of the body acts for any orientation of the body

Thank you