Engineering Mathematics Complex Variables Applications Chapter 2 wszhengieee

Engineering Mathematics Complex Variables & Applications Chapter 2 郑伟诗 wszheng@ieee. org, http: //sist. sysu. edu. cn/~zhwshi/

Complex Function & Mapping Definition:

Complex Function & Mapping Relationship between complex function and self-dependent variable For example,

Complex Function & Mapping
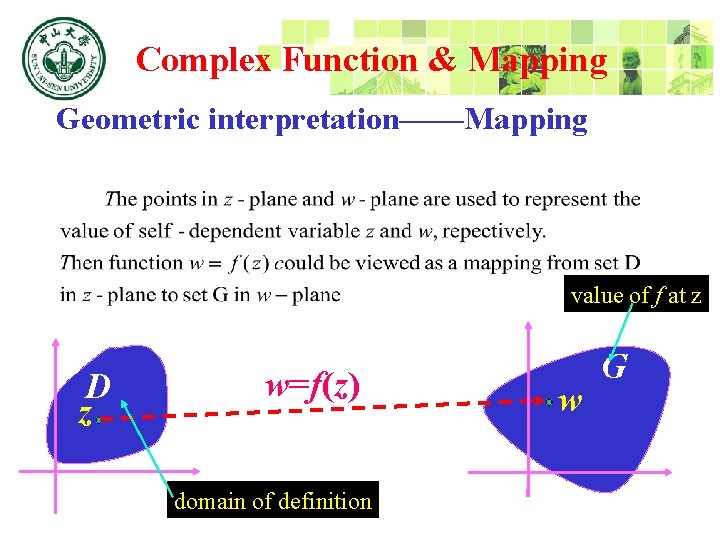
Complex Function & Mapping Geometric interpretation——Mapping Suppose there exist two complex plane,z-plane and w-plane value of f at z v y D z w=f(z) x domain of definition w G u
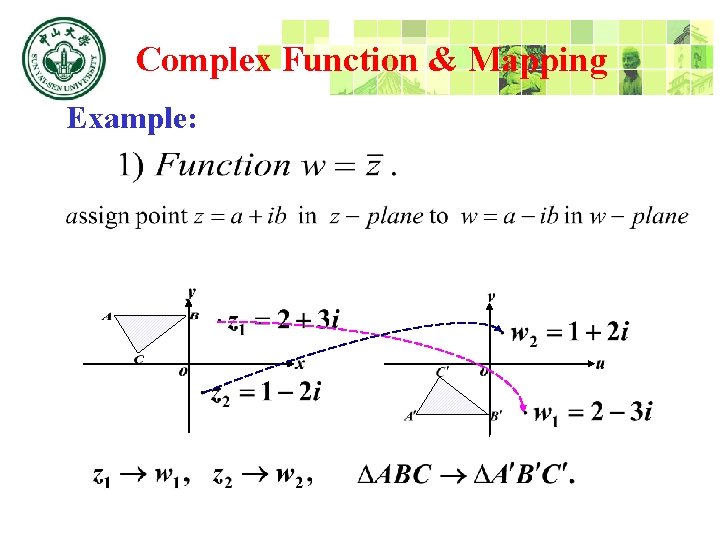
Complex Function & Mapping Example:
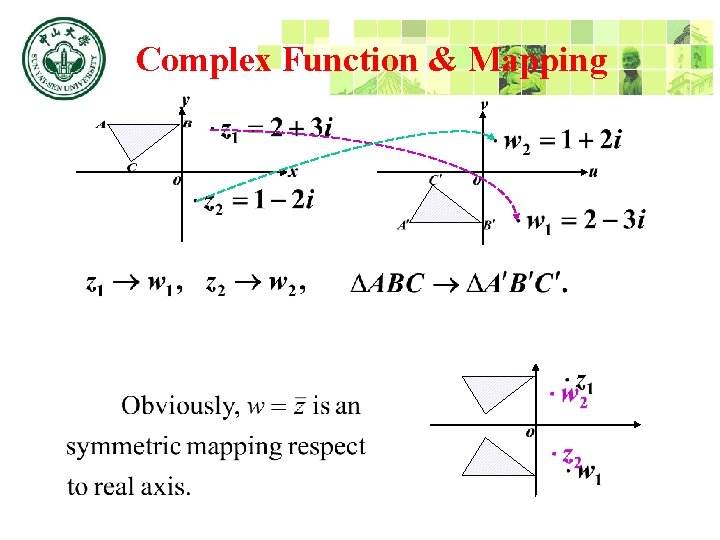
Complex Function & Mapping
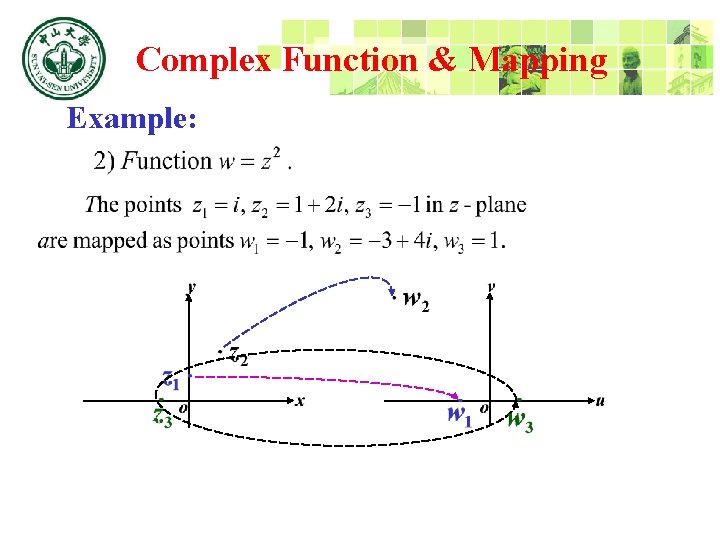
Complex Function & Mapping Example:
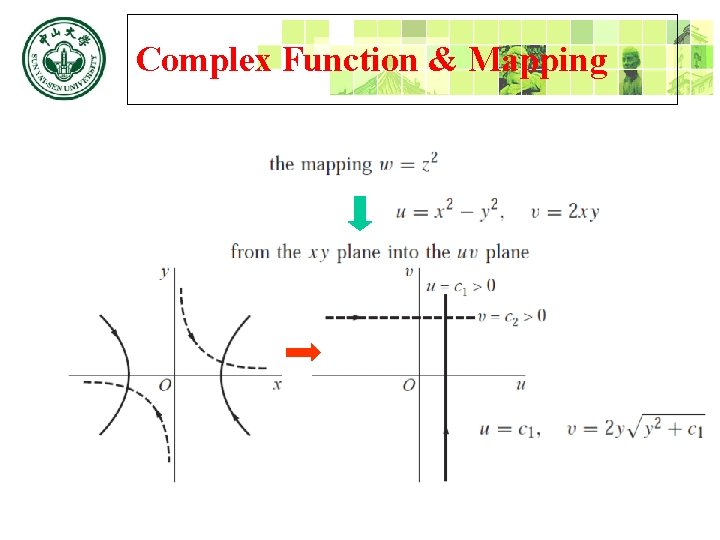
Complex Function & Mapping
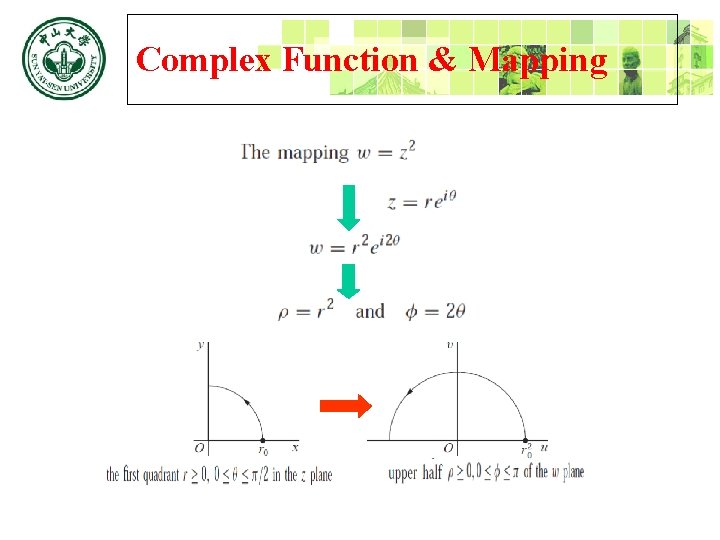
Complex Function & Mapping
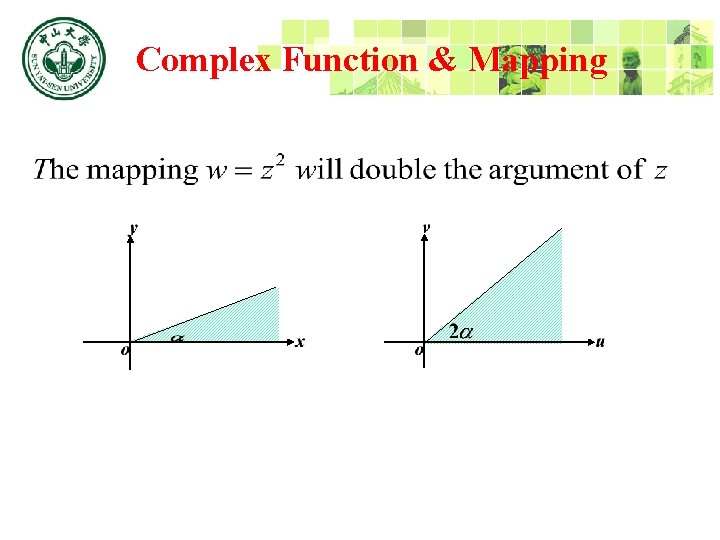
Complex Function & Mapping According to multiplicity rule,
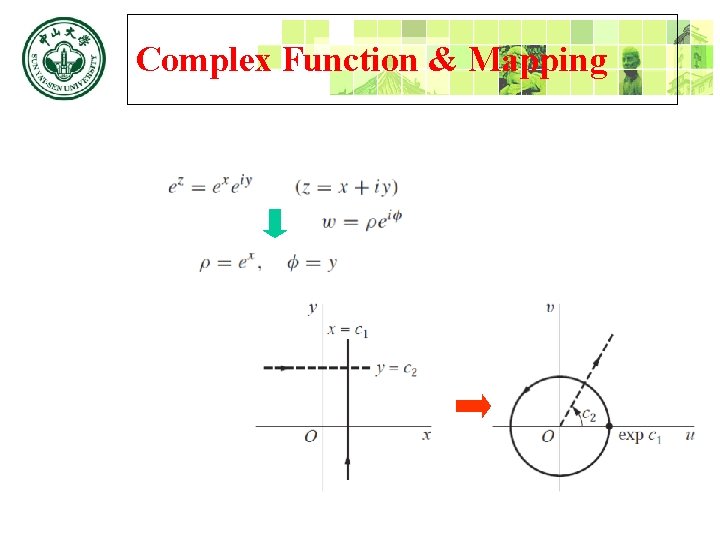
Complex Function & Mapping
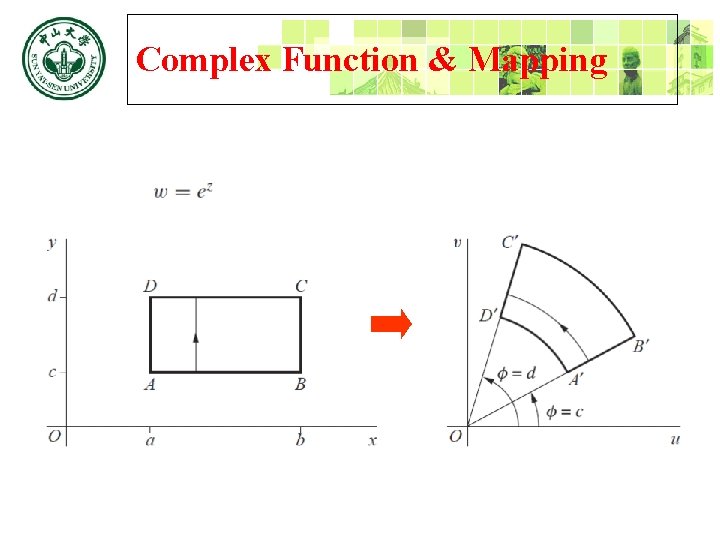
Complex Function & Mapping
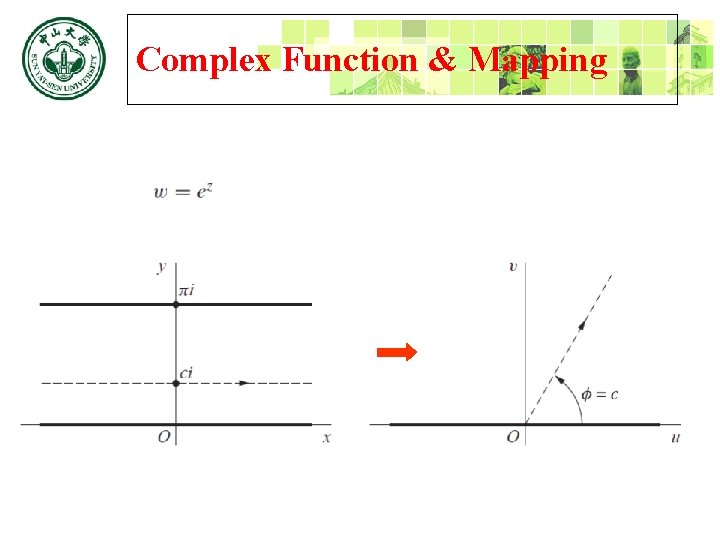
Complex Function & Mapping

Complex Function & Mapping • Polynomials

Complex Function & Mapping • Rational Function Polynomials

Complex Function & Mapping Single/multiple-valued functions

Complex Function & Mapping

Limit Definition: Remark:
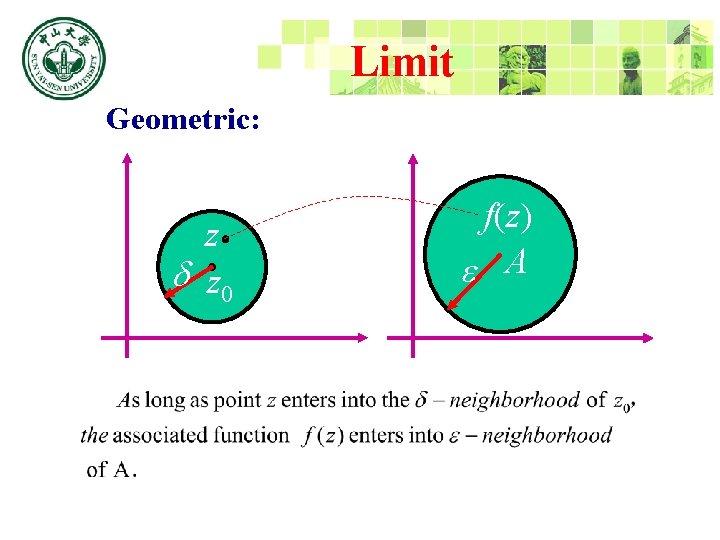
Limit Geometric: v y f(z) A z z 0 O x. O u

Limit 2. Theorems of Limits Theorem 1 Remark 板书证明

Limit Theorem 2

Limit • Proof using theorem 1

Limit Example 1 Proof: (i)

Limit From Theorem 1,

Limit Proof (ii)

Limit
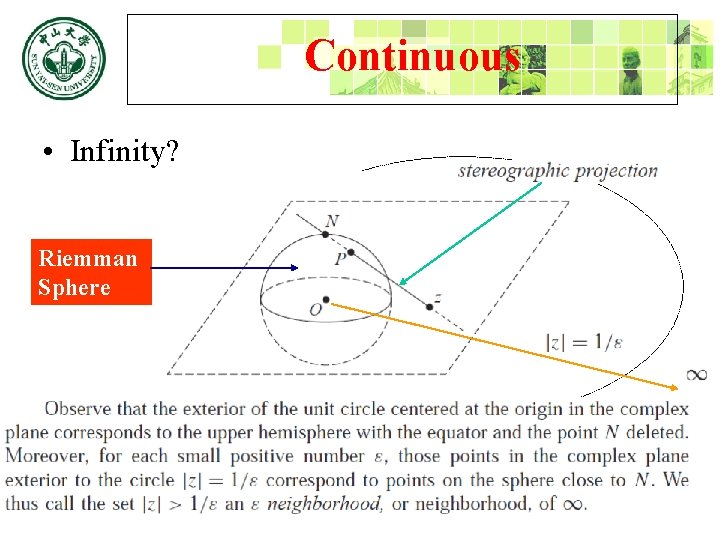
Continuous • Infinity? Riemman Sphere

Continuous Definition

Continuous

Continuous

Continuous

Continuous

Derivative Ex 2 Pf: y . O x

Derivative .

Derivative
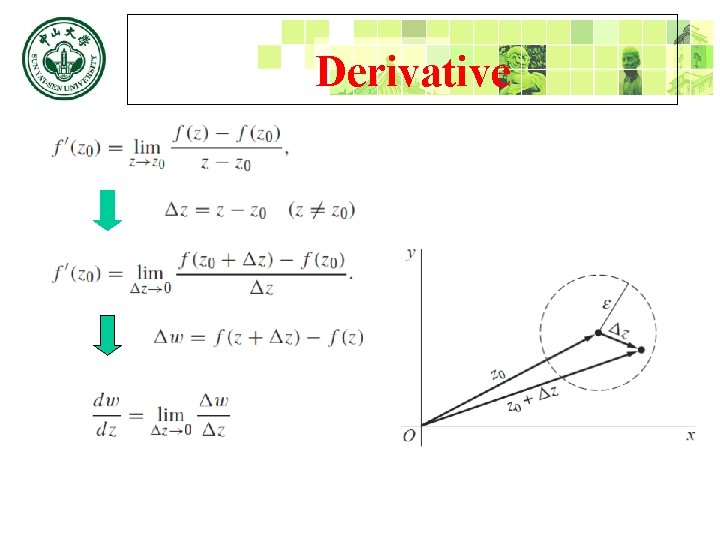
Derivative

Derivative
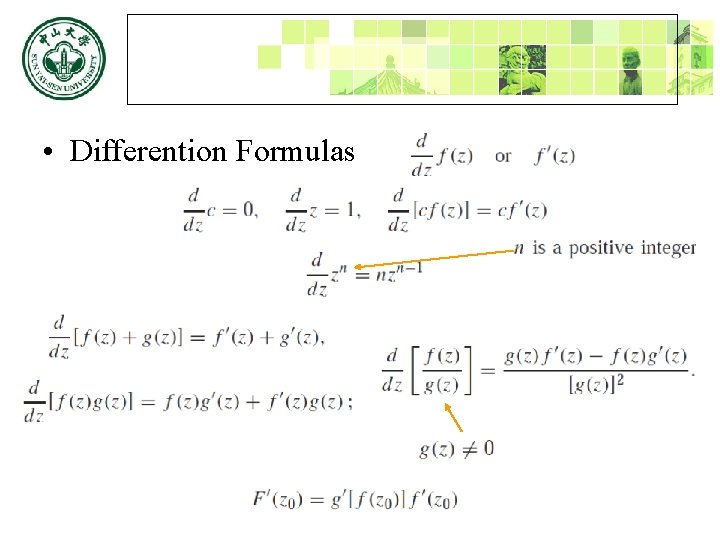
• Differention Formulas

Derivative

Derivative • Why? 板书证明

Derivative • Sufficient Conditions? Reversible?

Derivative SUFFICIENT CONDITIONS 板书证明

Derivative Can we derive the Cauchy-Riemman Equation in terms of Polar Coordinate?

Derivative

Derivative

Analytic Function • At a point Z 0 – Have derivative at each point in some neighborhood • In an open set – Have derivative everywhere at each point in the set • Entire Function Z – Analytic at each point in the entire plane 0 • Singular Point – Not Analytic around a point but analysis around in its every eighborhood
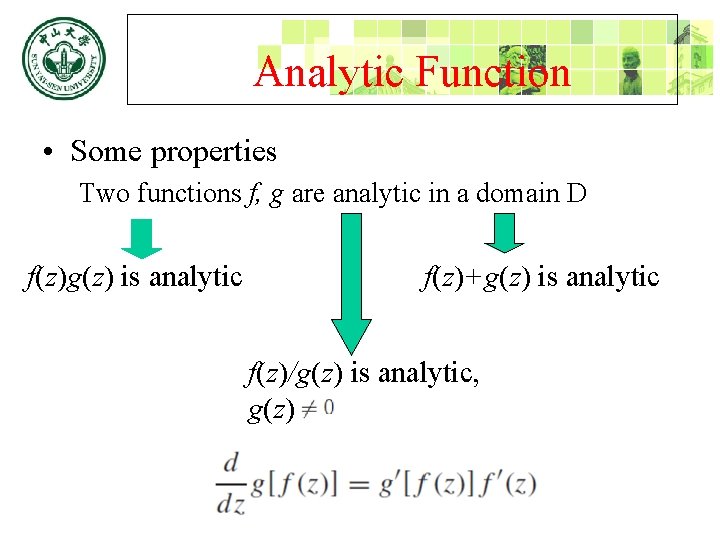
Analytic Function • Some properties Two functions f, g are analytic in a domain D f(z)g(z) is analytic f(z)+g(z) is analytic f(z)/g(z) is analytic, g(z)

Analytic Function • Examples vs.
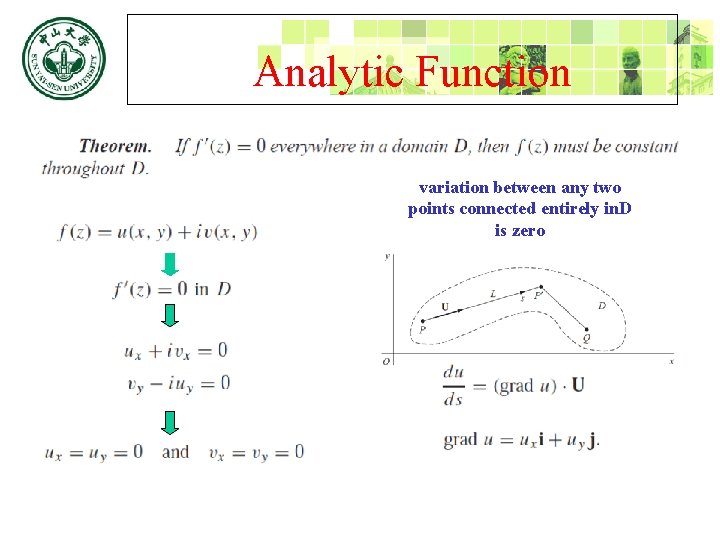
Analytic Function variation between any two points connected entirely in. D is zero

Analytic Function • Examples 板书

Analytic Function

Hamonic Function • H is harmonic in a domain D Has continuous paritial derivatives in D • First order • Second order A harmonic function defined on an annulus

Hamonic Function Cauchy Riemman Equations Chapter 4 Order Interchange

Hamonic Function • Harmonic conjugate

Analytic Functions: In depth

Examples *Example 1: Determine where the function is differentiable and analytic: *Solution:

Examples (exponential function) four partial derivatives are all continuous

Examples four partial derivatives are all continuous

Examples *Example 2: *Proof :

*Example 3: *Solution: Examples

Examples *Example 4: *Proof:

Examples

Examples *Example 5: *Solution :

Examples *Exercise: *Answer:

Examples *Example 6: *Proof:

Examples Referring to above example, we can prove further :

Examples *Example 7: *Proof : By derivation rules on implicity function,

Examples

Examples *Example 8: *Proof:

Examples
Examples • Let's have something funny! http: //www. youtube. com/watch? v=mu 2 da. K 7 cf. B 4
- Slides: 72