Engineering HL The Option Fluids Density Pressure Pressure

Practice! Bubba has a mass of 112 kg and a volume of 0. 11

Pascal A hydraulic system is set up in equilibrium with two pistons, one with

Bernoulli A large vat of water has a total height of 1 m, when

Stokes Law Carbonated Water is simply water with dissolved Carbon Dioxide. The Carbon Dioxide

Reynolds Number Oil flows through a pipe of diameter 30 mm with a velocity

Q Factor An electrical pendulum clock has a period of 1. 0 s. An

Slides: 42

Download presentation

Engineering - HL The Option

Fluids

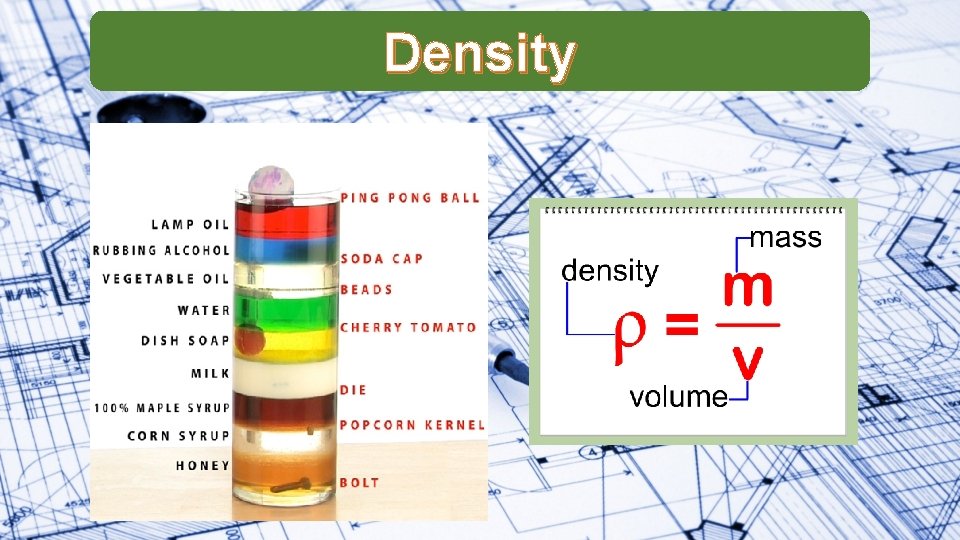
Density

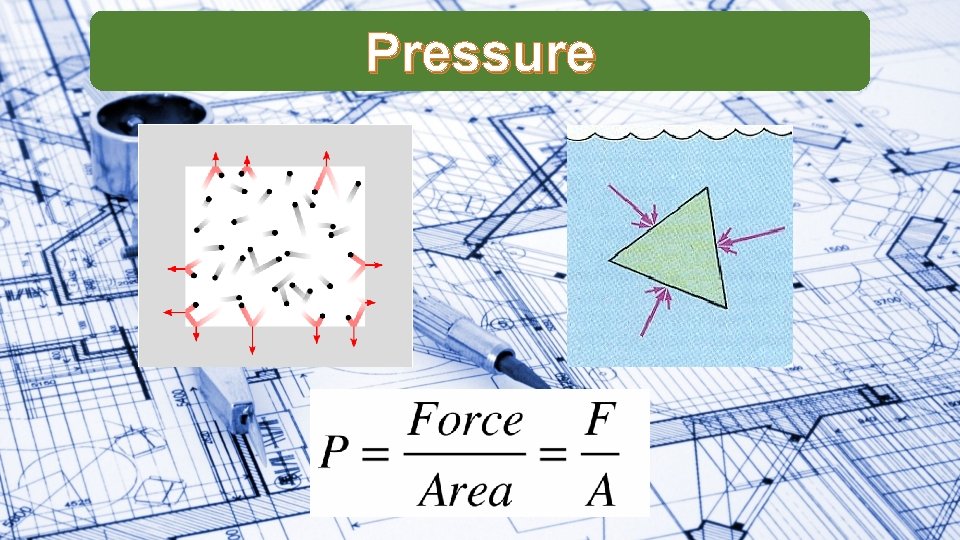
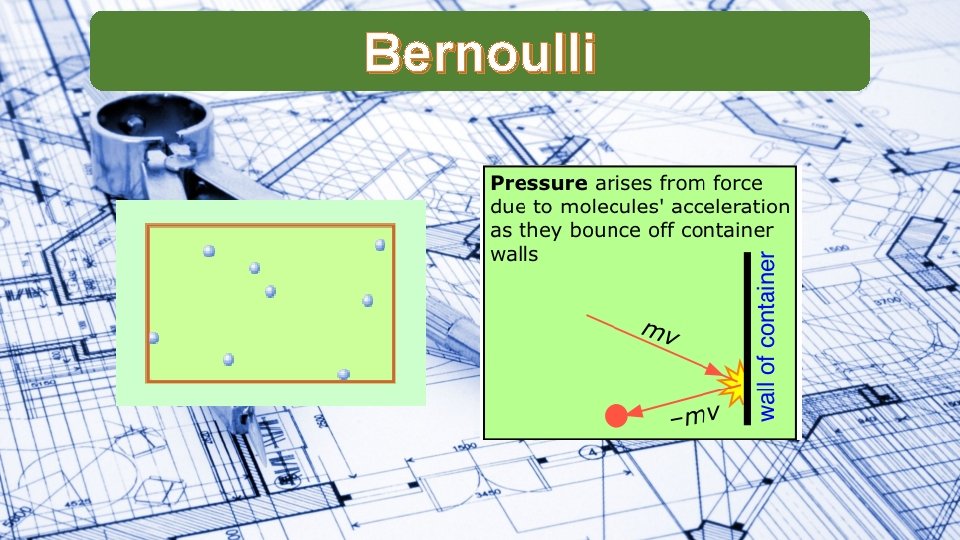
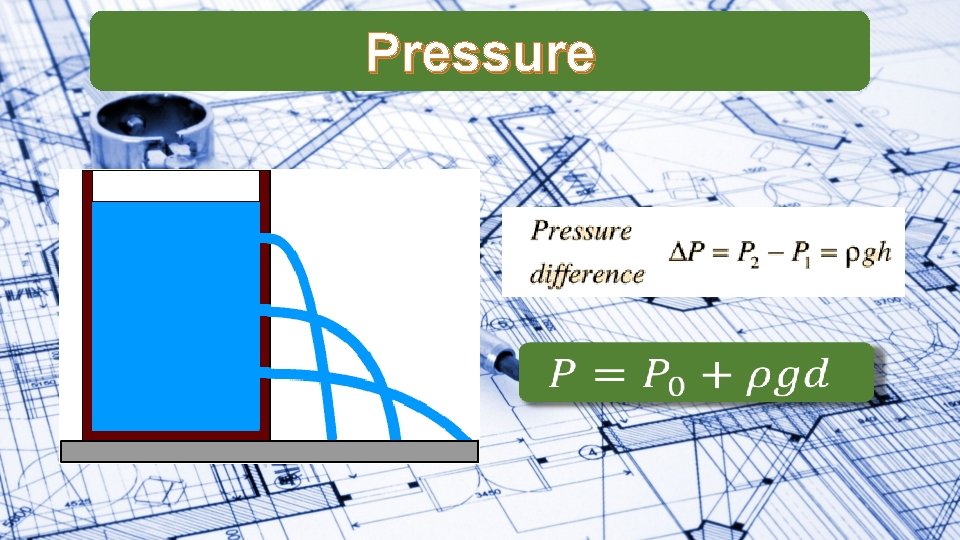
Pressure

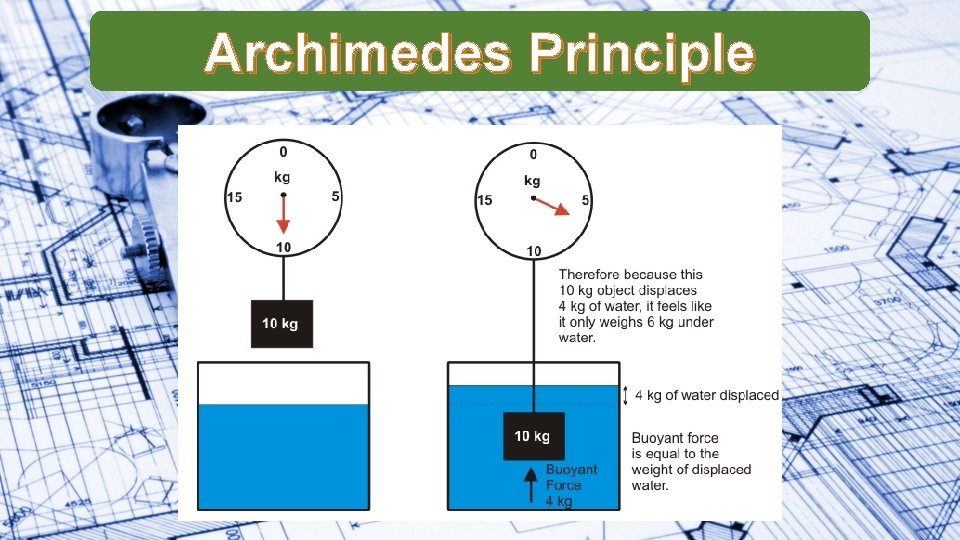
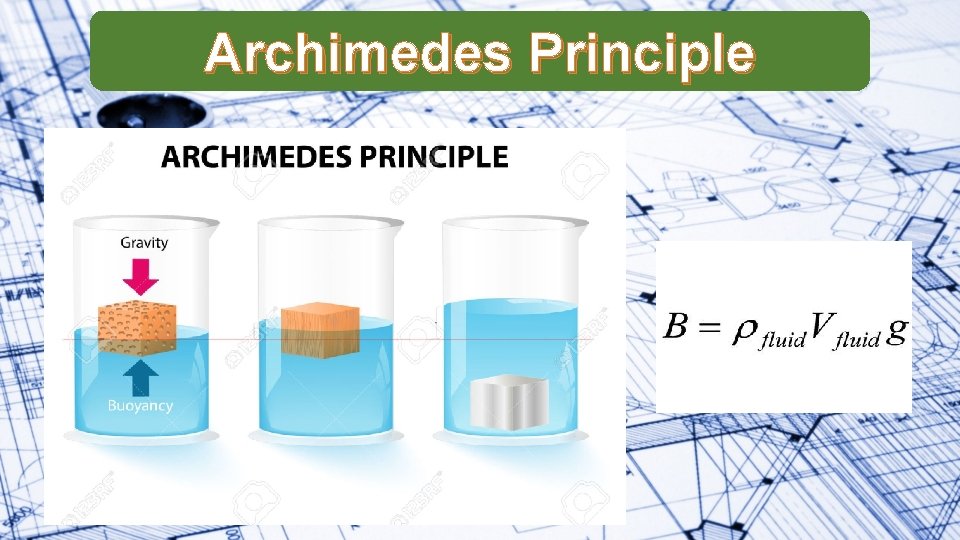
Archimedes Principle

Continuity

Practice! Bubba has a mass of 112 kg and a volume of 0. 11 m 3. First he jumps in his swimming pool (density of 1000 kg m-3). Next he jumps in the ocean (density of 1027 kg m-3). And finally he jumps into the dead sea (density 1240 kg m-3). What volume of water does he displace in each? Does he float or sink? A water pipe has a radius of 5 cm and water flows through with a speed of 0. 4 ms-1. Determine the volume flow rate of through the tube in m 3 s-1. The tube narrows to a radius of 2 cm. Determine the new velocity of the water.

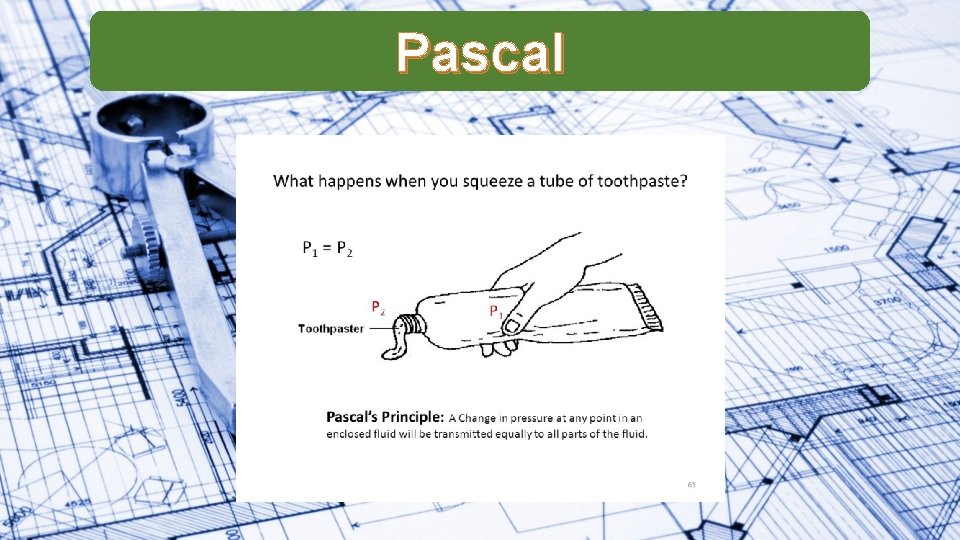
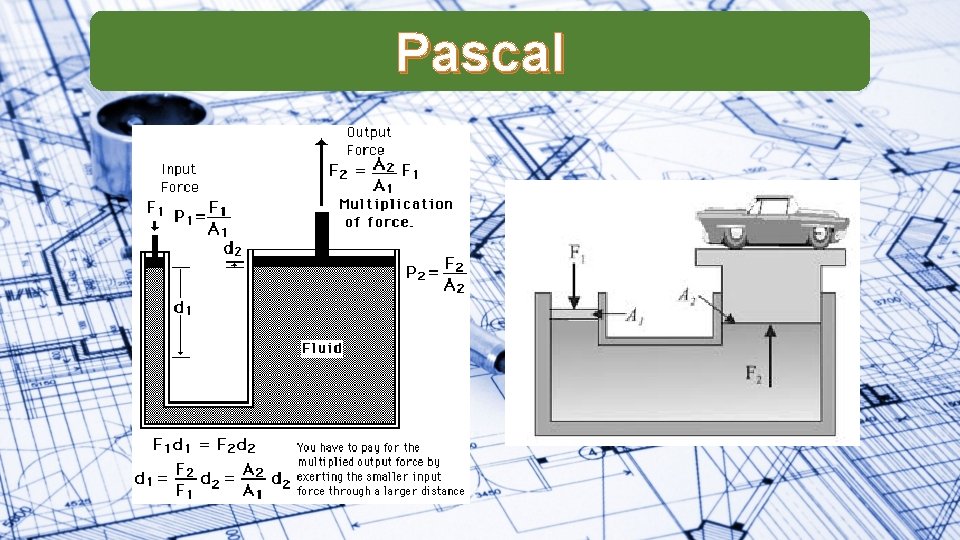
Pascal

Pascal A hydraulic system is set up in equilibrium with two pistons, one with radius 3 cm and one with radius 50 cm. A force of 20 N is applied to the small radius. • Determine the output force from the larger piston. • The small piston is moved over a distance of 30 cm. Determine the work done by the input force. • Determine the volume of fluid displaced by the input piston. • Determine the distance moved by the output force. • Determine the work done by the output force.

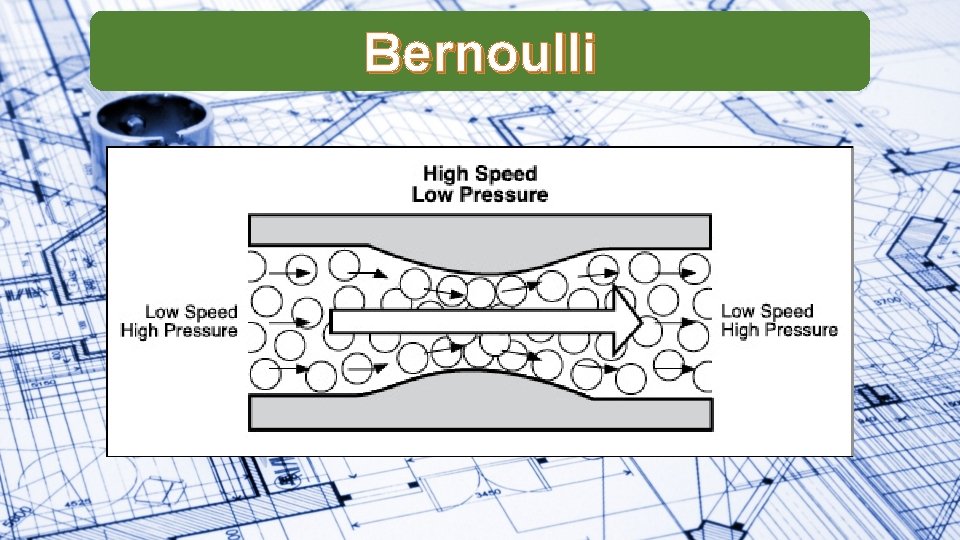
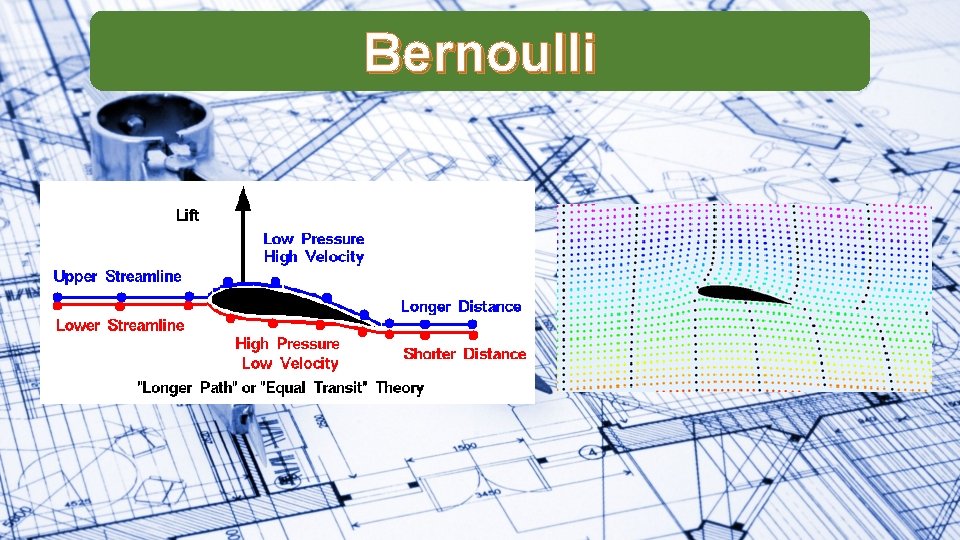
Bernoulli

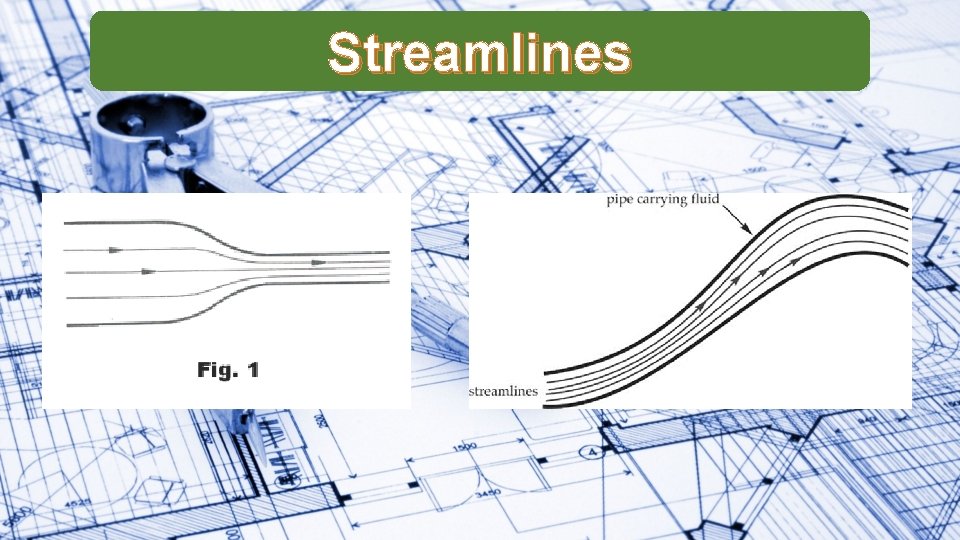
Streamlines

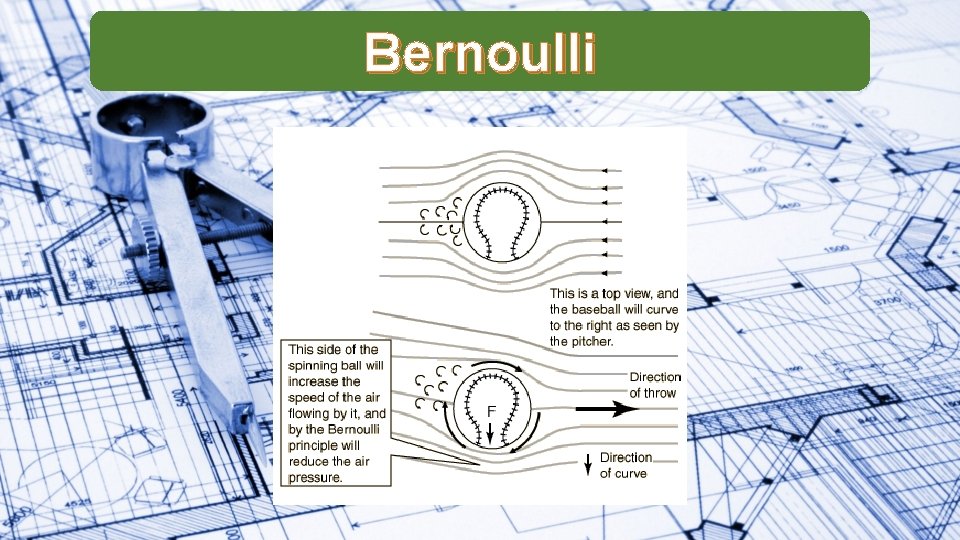
Bernoulli

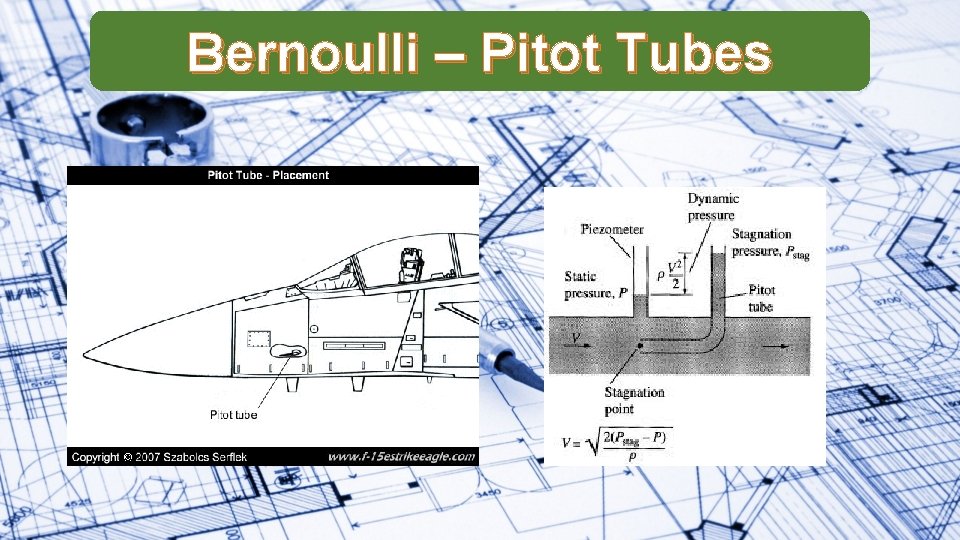
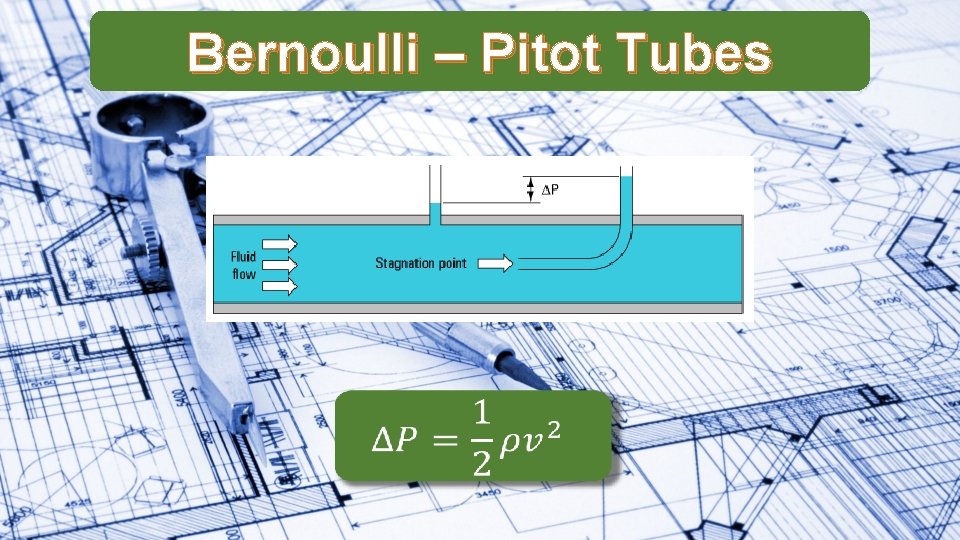
Bernoulli – Pitot Tubes

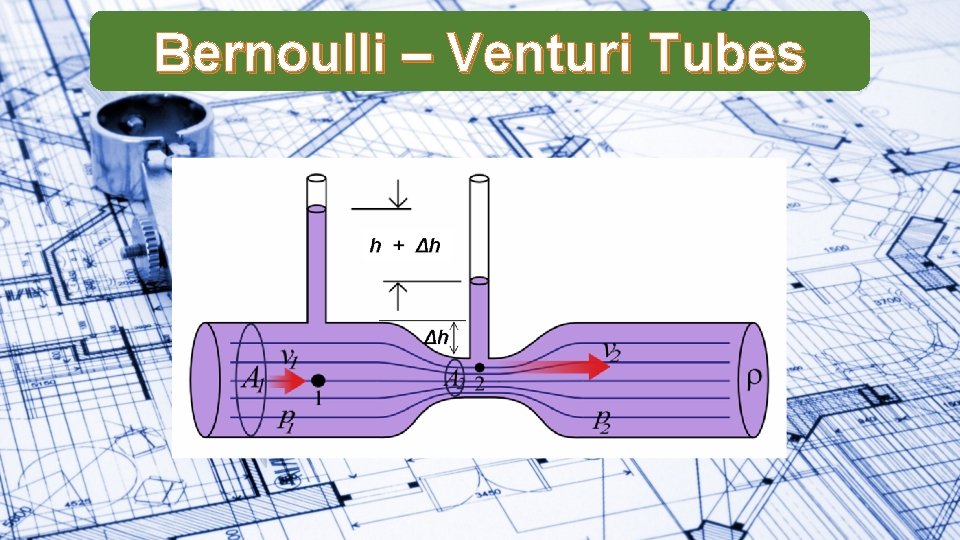
Bernoulli – Venturi Tubes

Bernoulli A large vat of water has a total height of 1 m, when a leak appears from a small hole 0. 2 m above the base. Determine the velocity of the water as it exits the vat. Determine how far from the base of the vat the water lands. The diagram shows a venture meter with a mercury manometer set up to measure the pressure differences between a horizontal pipe. The difference in height of the arms of the manometer are 80 mm. Calculate the pressure difference in Pascals (density of mercury = 1. 4 x 104 kgm-3). The cross-sectional areas of the pipe and venturi meter are 4 x 10 -2 m 2 and 1 x 10 -2 m 2 respectively. Determine the ratio of the speed of the liquid (density 8 x 102 kg/m 3) in the narrow meter to the speed of the liquid in the pipe. Use Bernoulli’s equation to estimate the speed of the liquid in the pipe.

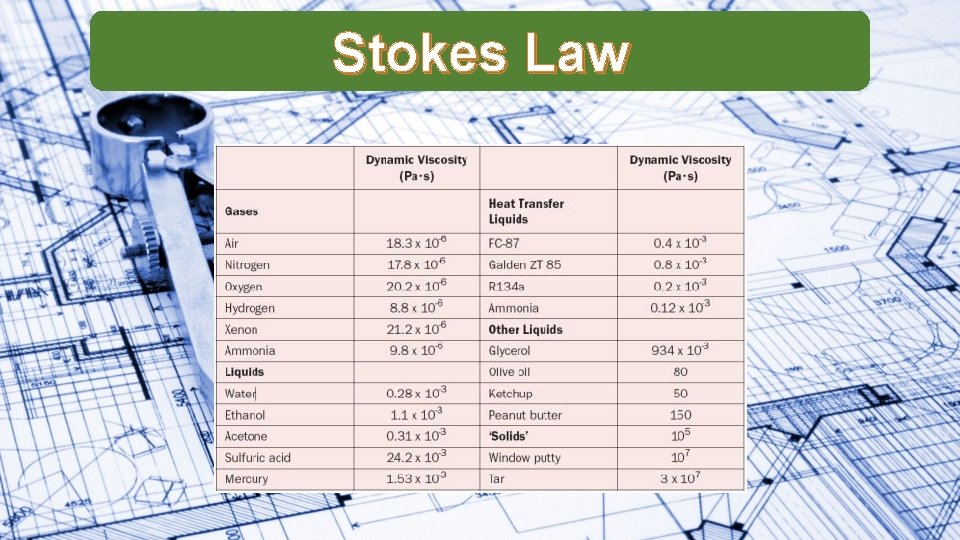
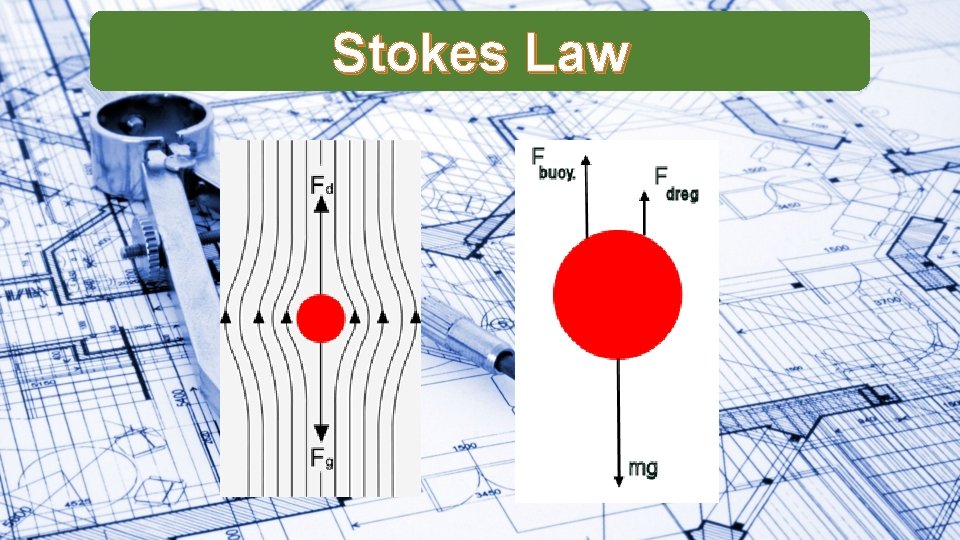
Stokes Law

Stokes Law Carbonated Water is simply water with dissolved Carbon Dioxide. The Carbon Dioxide can form small bubbles, displacing the water (density of 1000 kg m-3) and creating a buoyant force. As a result the bubble accelerates upwards, with an increasing drag force until they reach a terminal upwards velocity. Given a bubble with radius 1 mm, determine the buoyant force on the bubble. If the coefficient of viscosity is 0. 28 x 10 -3 Pa s, what is the speed of the bubble once terminal velocity is reached? How does this change if the radius is doubled?

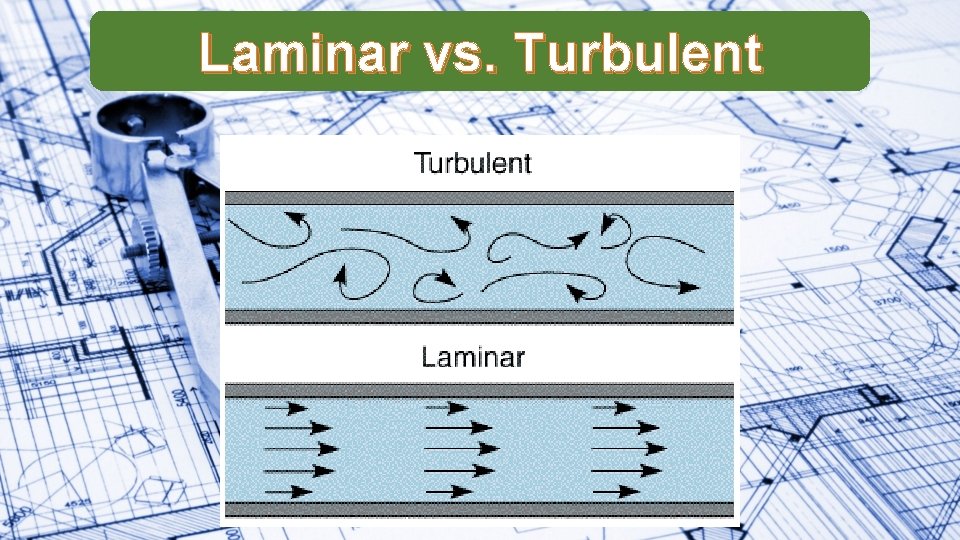
Laminar vs. Turbulent

Reynolds Number

Reynolds Number Oil flows through a pipe of diameter 30 mm with a velocity of 2. 5 m s− 1. The oil has viscosity 0. 30 Pa s and density of 890 kg m− 3 a) Determine whether or not this flow is laminar. b) Calculate the maximum velocity at which the oil will flow through the pipe and still remain laminar.

Checkpoint…

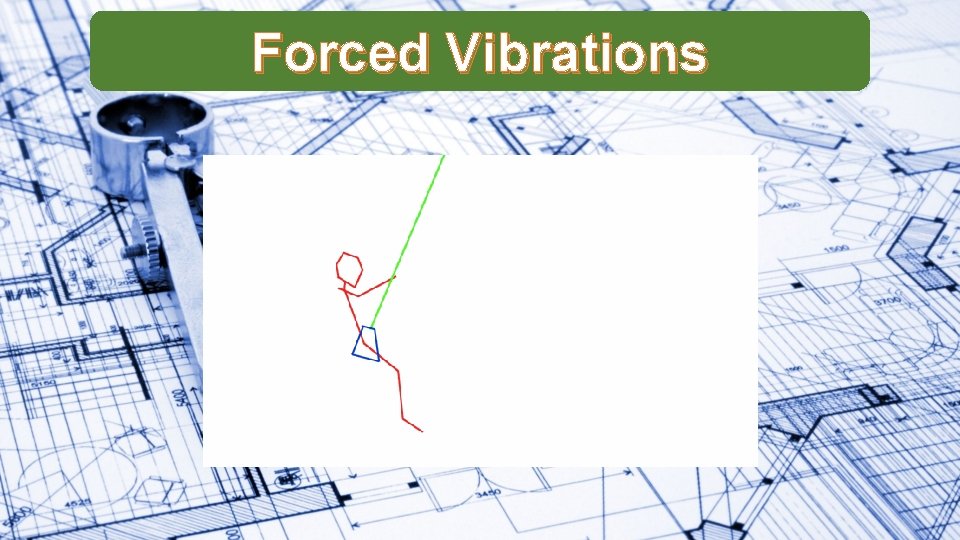
Forced Vibrations

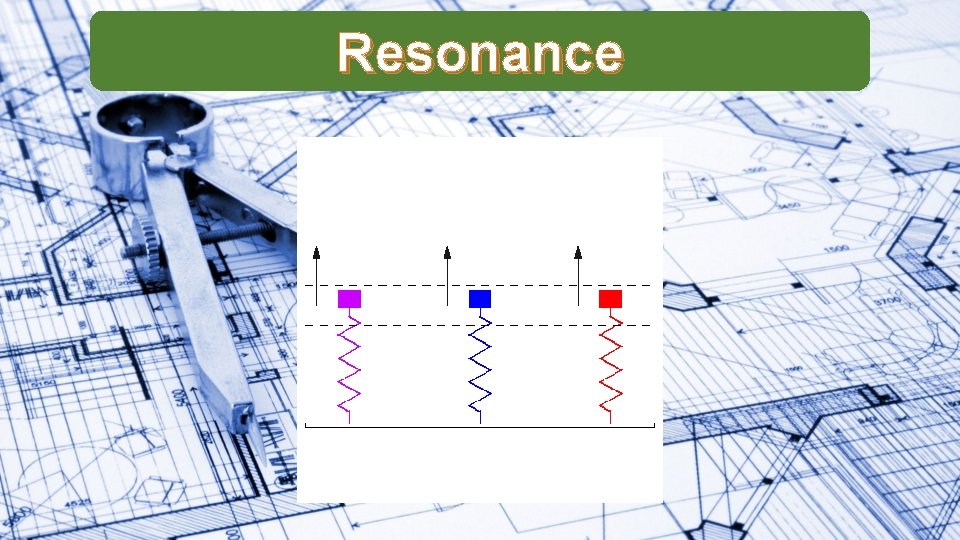
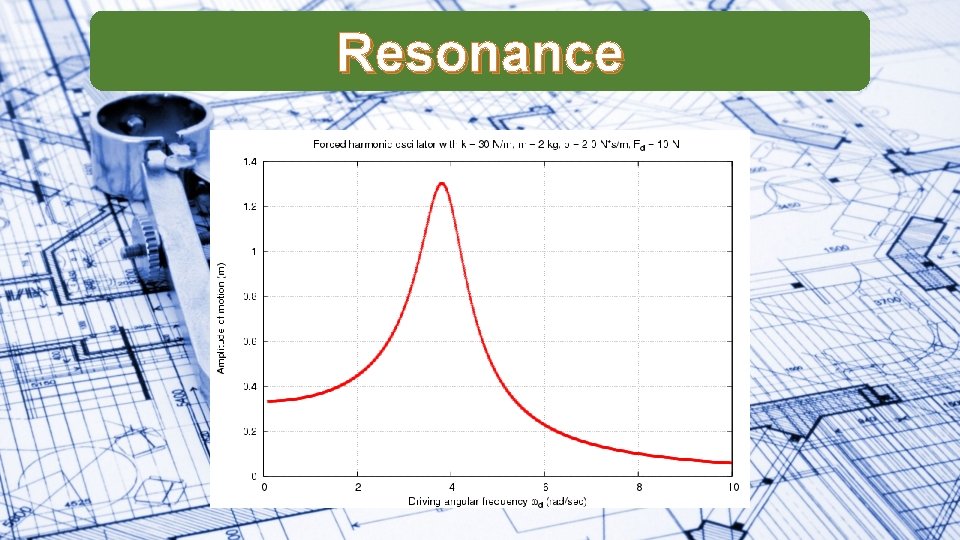
Resonance

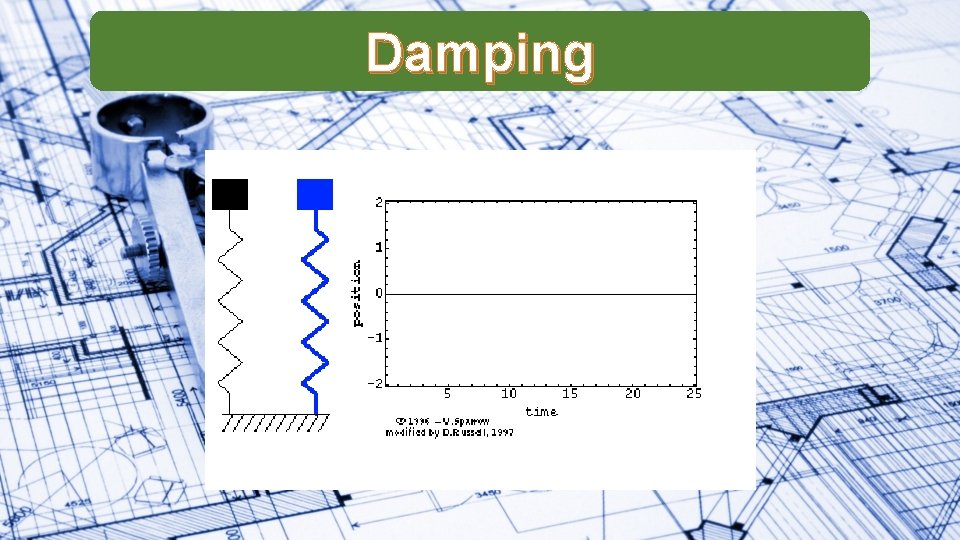
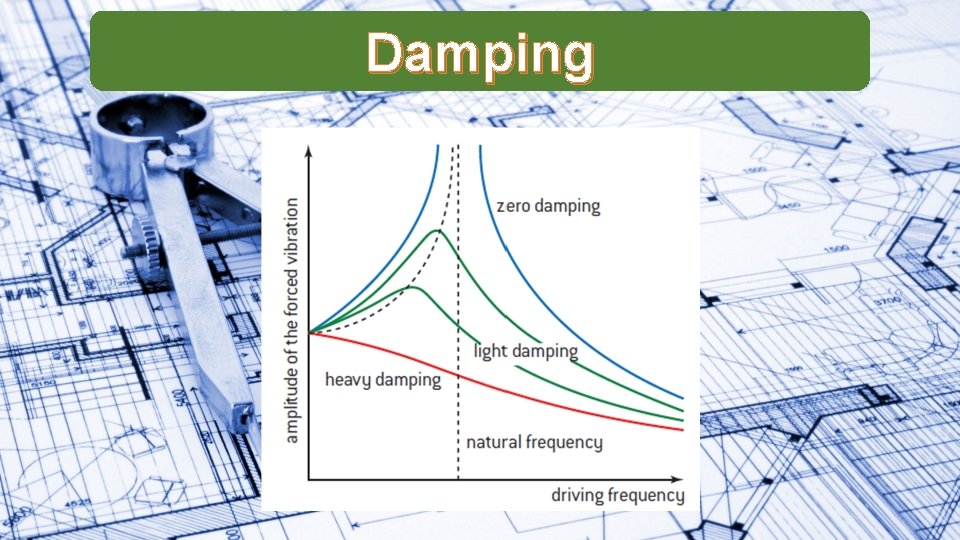
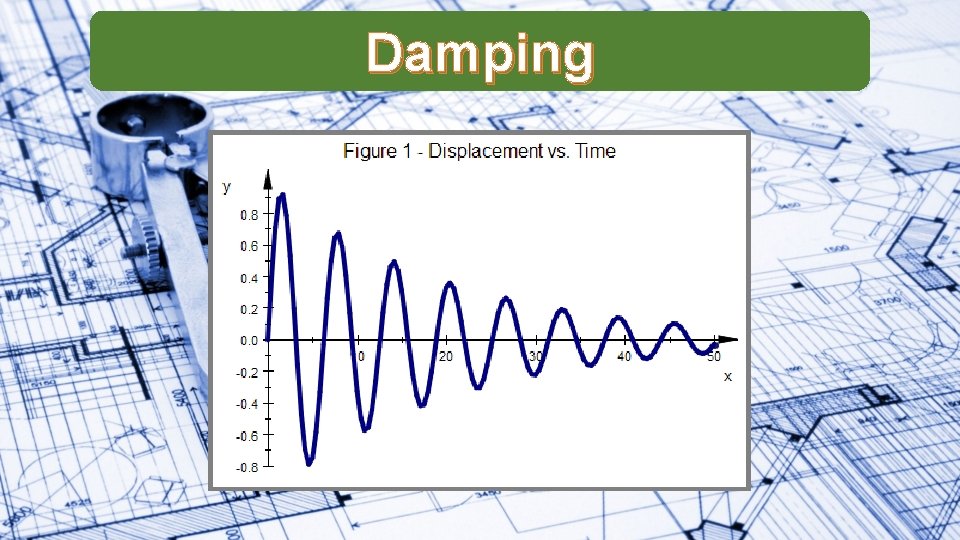
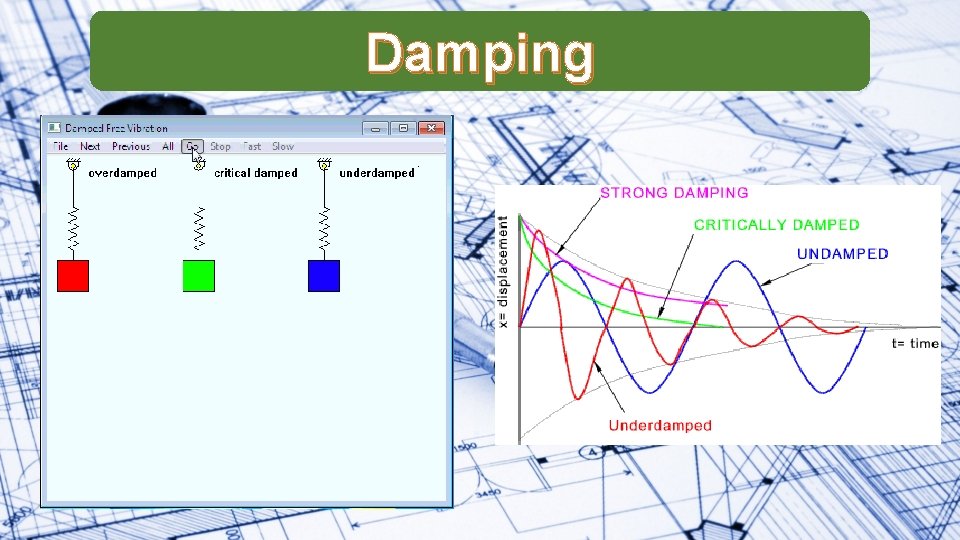
Damping

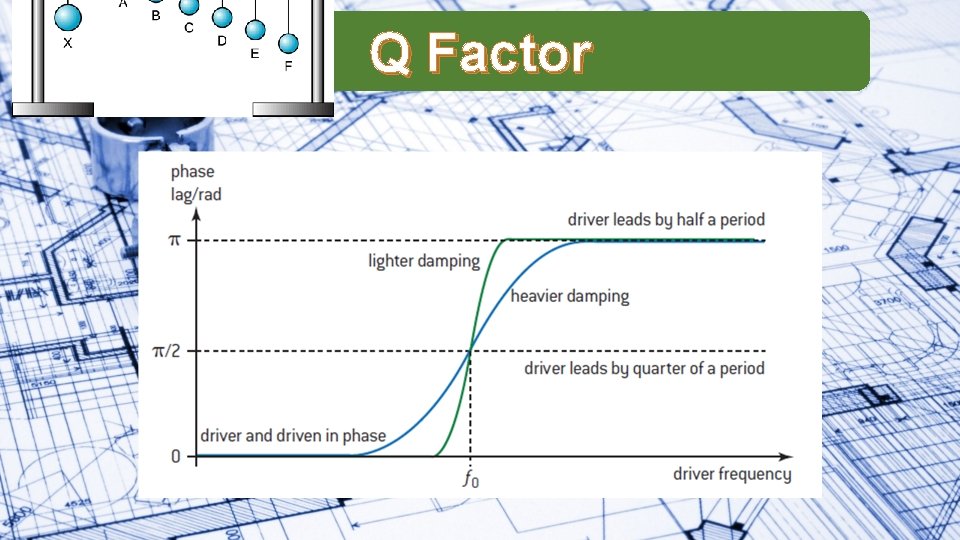
Q Factor

Q Factor An electrical pendulum clock has a period of 1. 0 s. An electrical power supply of 25 m. W maintains its constant amplitude. As the pendulum passes its equilibrium position it has kinetic energy of 40 m. J. Calculate the Q factor for the pendulum clock.

Q Factor