Engineering Electromagnetics W H Hayt Jr and J























- Slides: 29

Engineering Electromagnetics W. H. Hayt Jr. and J. A. Buck Chapter 5: Conductors and Dielectrics

Current and Current Density Current is a flux quantity and is defined as: Current density, J, measured in Amps/m 2 , yields current in Amps when it is integrated over a cross-sectional area. The assumption would be that the direction of J is normal to the surface, and so we would write:

Current Density as a Vector Field In reality, the direction of current flow may not be normal to the surface in question, so we treat current density as a vector, and write the incremental flux through the small surface in the usual way: where S = n da n Then, the current through a large surface is found through the flux integral:

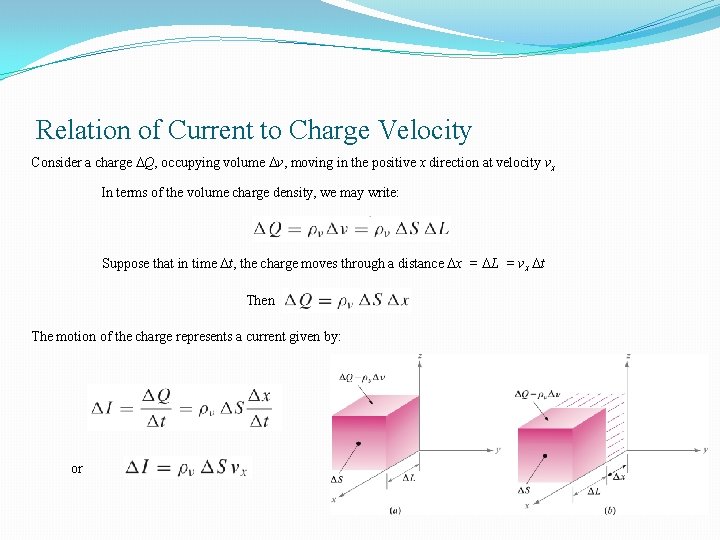
Relation of Current to Charge Velocity Consider a charge Q, occupying volume v, moving in the positive x direction at velocity vx In terms of the volume charge density, we may write: Suppose that in time t, the charge moves through a distance x = L = vx t Then The motion of the charge represents a current given by: or

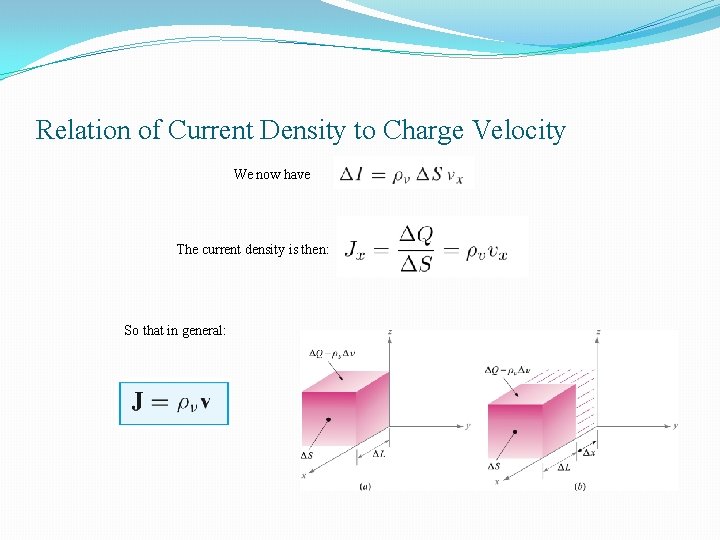
Relation of Current Density to Charge Velocity We now have The current density is then: So that in general:

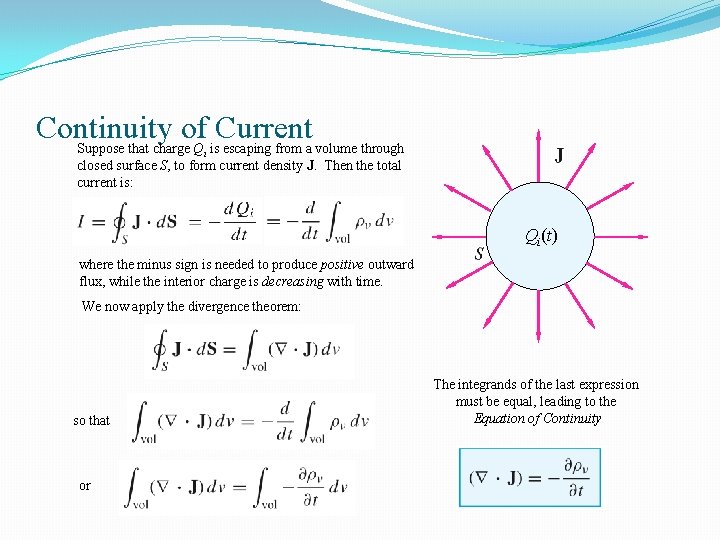
Continuity of Current Suppose that charge Q is escaping from a volume through i closed surface S, to form current density J. Then the total current is: Qi(t) where the minus sign is needed to produce positive outward flux, while the interior charge is decreasing with time. We now apply the divergence theorem: so that or The integrands of the last expression must be equal, leading to the Equation of Continuity

Energy Band Structure in Three Material Types a) b) c) Conductors exhibit no energy gap between valence and conduction bands so electrons move freely Insulators show large energy gaps, requiring large amounts of energy to lift electrons into the conduction band When this occurs, the dielectric breaks down. Semiconductors have a relatively small energy gap, so modest amounts of energy (applied through heat, light, or an electric field) may lift electrons from valence to conduction bands.

Electron Flow in Conductors Free electrons move under the influence of an electric field. The applied force on an electron of charge Q = -e will be When forced, the electron accelerates to an equilibrium velocity, known as the drift velocity: where e is the electron mobility, expressed in units of m 2/V-s. The drift velocity is used to find the current density through: The expression: from which we identify the conductivity for the case of electron flow : In a semiconductor, we have hole current as well, and S/m is Ohm’s Law in point form

Resistance Consider the cylindrical conductor shown here, with voltage V applied across the ends. Current flows down the length, and is assumed to be uniformly distributed over the cross-section, S. First, we can write the voltage and current in the cylinder in terms of field quantities: Using Ohm’s Law: We find the resistance of the cylinder: a b

Electrostatic Properties of Conductors Consider a conductor, on which excess charge has been placed E + + ++ + + s solid conductor E = 0 inside + + + + + Electric field at the surface points in the normal direction 1. Charge can exist only on the surface as a surface charge density, s -- not in the interior. 2. Electric field cannot exist in the interior, nor can it possess a tangential component at the surface (as will be shown next slide). 3. It follows from condition 2 that the surface of a conductor is an equipotential.

Tangential Electric Field Boundary Condition Over the rectangular integration path, we use or To find: These become negligible as h approaches zero. dielectric Therefore n More formally: conductor

Boundary Condition for the Normal Component of D Gauss’ Law is applied to the cylindrical surface shown below: This reduces to: dielectric as h approaches zero Therefore n More formally: s conductor

Summary Tangential E is zero At the surface: Normal D is equal to the surface charge density

Method of Images Theorem of Uniqueness states that if we are given a configuration of charges and boundary conditions, there will exist only one potential and electric field solution. In the electric dipole, the surface along the plane of symmetry is an equipotential with V = 0. The same is true if a grounded conducting plane is located there. So the boundary conditions and charges are identical in the upper half spaces of both configurations (not in the lower half). In effect, the positive point charge images across the conducting plane, allowing the conductor to be replaced by the image. The field and potential distribution in the upper half space is now found much more easily!

Forms of Image Charges Each charge in a given configuration will have its own image

Electric Dipole and Dipole Moment In dielectric, charges are held in position (bound), and ideally there are no free charges that can move and form a current. Atoms and molecules may be polar (having separated positive and negative charges), or may be polarized by the application of an electric field. Consider such a polarized atom or molecule, which possesses a dipole moment, p, defined as the charge magnitude present, Q, times the positive and negative charge separation, d. Dipole moment is a vector that points from the negative to the positive charge. d Q p = Qd ax

Model of a Dielectric A dielectric can be modeled as an ensemble of bound charges in free space, associated with the atoms and molecules that make up the material. Some of these may have intrinsic dipole moments, others not. In some materials (such as liquids), dipole moments are in random directions.

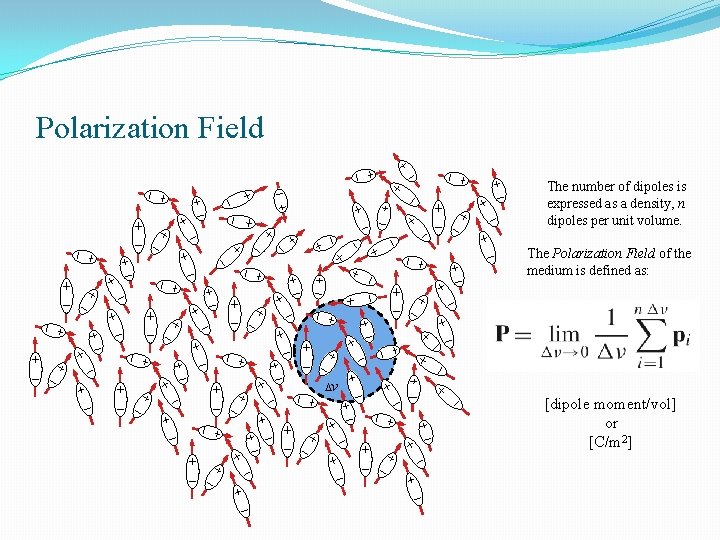
Polarization Field The number of dipoles is expressed as a density, n dipoles per unit volume. The Polarization Field of the medium is defined as: v [dipole moment/vol] or [C/m 2]

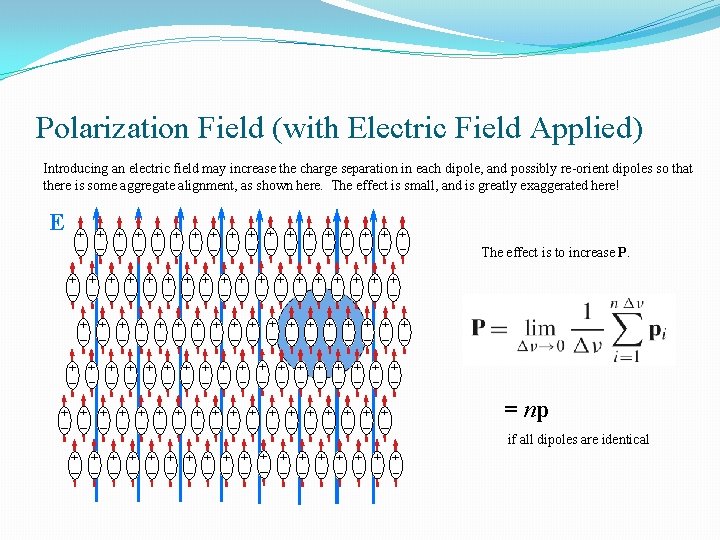
Polarization Field (with Electric Field Applied) Introducing an electric field may increase the charge separation in each dipole, and possibly re-orient dipoles so that there is some aggregate alignment, as shown here. The effect is small, and is greatly exaggerated here! E The effect is to increase P. = np if all dipoles are identical

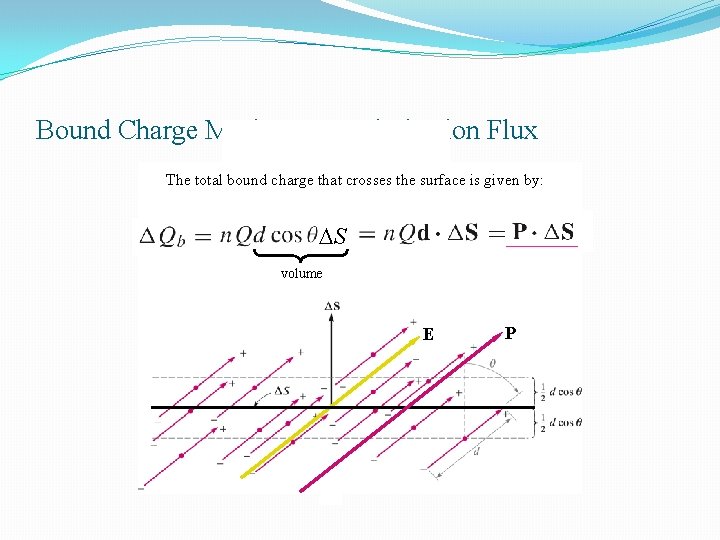
Migration of Bound Charge Consider an electric field applied at an angle to a surface normal as shown. The resulting separation of bound charges (or re-orientation) leads to positive bound charge crossing upward through surface of area S, while negative bound charge crosses downward through the surface. Dipole centers (red dots) that lie within the range (1/2) d cos above or below the surface will transfer charge across the surface. E

Bound Charge Motion as a Polarization Flux The total bound charge that crosses the surface is given by: S volume E P

Polarization Flux Through a Closed Surface The accumulation of positive bound charge within a closed surface means that the polarization vector must be pointing inward. Therefore: S - + + qb - P -

Bound and Free Charge Now consider the charge within the closed surface consisting of bound charges, qb , and free charges, q. The total charge will be the sum of all bound and free charges. We write Gauss’ Law in terms of the total charge, QT as: where free charge QT = Q b + Q bound charge E QT S q+ + + + +q b P

Gauss. We. Law for Free Charge now have: and where QT = Q b + Q combining these, we write: we thus identify: which we use in the familiar form of Gauss’ Law:

Charge Densities Taking the previous results and using the divergence theorem, we find the point form expressions: Bound Charge: Total Charge: Free Charge:

Electric Susceptibility and the Dielectric Constant A stronger electric field results in a larger polarization in the medium. In a linear medium, the relation between P and E is linear, and is given by: where e is the electric susceptibility of the medium. We may now write: where the dielectric constant, or relative permittivity is defined as: Leading to the overall permittivity of the medium: where

Isotropic vs. Anisotropic Media In an isotropic medium, the dielectric constant is invariant with direction of the applied electric field. This is not the case in an anisotropic medium (usually a crystal) in which the dielectric constant will vary as the electric field is rotated in certain directions. In this case, the electric flux density vector components must be evaluated separately through the dielectric tensor. The relation can be expressed in the form:

Boundary Condition for Tangential Electric Field We use the fact that E is conservative: n So therefore: Region 1 1 Region 2 2 Leading to: More formally:

Boundary Condition for Normal Electric Flux Density We apply Gauss’ Law to the cylindrical volume shown here, in which cylinder height is allowed to approach zero, and there is charge density s on the surface: n Region 1 1 s Region 2 2 The electric flux enters and exits only through the bottom and top surfaces, respectively. More formally: From which: and if the charge density is zero:
 Advanced engineering electromagnetics
Advanced engineering electromagnetics Intensity of magnetic field
Intensity of magnetic field Engineering electromagnetics
Engineering electromagnetics Engineering electromagnetics
Engineering electromagnetics Engineering electromagnetics
Engineering electromagnetics Hayt
Hayt Hayt
Hayt Hayt
Hayt Hayt
Hayt Hayt
Hayt Cheng field and wave electromagnetics
Cheng field and wave electromagnetics Image theory in electromagnetics
Image theory in electromagnetics Able electromagnetics
Able electromagnetics Electromagnetics
Electromagnetics Able electromagnetics
Able electromagnetics Shorted stub
Shorted stub Electromagnetics
Electromagnetics Electromagnetics
Electromagnetics Electromagnetics
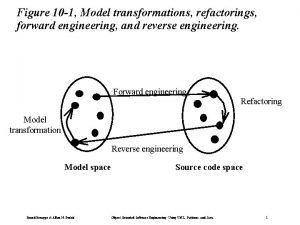
Electromagnetics Forward engineering and reverse engineering
Forward engineering and reverse engineering Computer based system engineering
Computer based system engineering Dicapine
Dicapine Elegant systems
Elegant systems Forward and reverse engineering
Forward and reverse engineering Cost analysis and estimating for engineering and management
Cost analysis and estimating for engineering and management Alstom and mbse
Alstom and mbse Cost analysis and estimating for engineering and management
Cost analysis and estimating for engineering and management Cost analysis and estimating for engineering and management
Cost analysis and estimating for engineering and management Cost analysis and estimating for engineering and management
Cost analysis and estimating for engineering and management Cost analysis and estimating for engineering and management
Cost analysis and estimating for engineering and management