Engineering Economic Analysis Chapter 14 Inflation and Price

Engineering Economic Analysis Chapter 14 Inflation and Price Change 10/19/2021 rd 1

Inflation Rate Factors Cost of energy Interest rates Availability and cost of skilled people Scarcity of materials Political stability Inflation is the increase in the amount of money necessary to buy the same amount of a product or service over time. Government prints more dollars (weakens value) while the supply of goods does not increase. Same dollar amount buys less. 10/19/2021 rd 2

Inflation Problems Inflation causes a redistribution of wealth. Some profit while other suffer. (Oil companies, truck drivers) Price Effects – Oil companies make obscene profits Wealth effects – Hurts lenders but benefits borrowers. 10/19/2021 rd 3

Combating Inflation Fix costs and allow income to increase. Fix costs by entering into long-term contracts for material and labor, by buying materials before they are needed by stockpiling products for sale later. Borrowing becomes more attractive in inflationary times since debt is repaid in cheaper dollars. 10/19/2021 rd 4

Inflation A$ Actual Dollars, nominal, inflated, future, then-current R$ Real Dollars, constant-value, today, relative to base year f General price inflation rate im Market interest rate ir Real or effective interest rate Base time period 10/19/2021 rd 5

Inflation Rate ~ f Market Rate ~ im Real Rate ~ ir R$ = A$(1 + f)-n A$ brought back to the base year A$ = R$(1 + f)n R$ inflated to the current year Bank interest rates reflect a real rate plus an expected inflation rate. Real rate is typically near the rate of a US Treasury bond (safest investment). 10/19/2021 rd 6

Inflation and Price Indexes Construction Cost Index Average % Year Index value rate/year 1950 510 --1955 660 5. 3 660 = 510(1 + i)5 => i = 5. 29 1960 824 4. 5 824 = 660(1 + i)5 => i = 4. 54 …. 1995 5471 6. 11 5471 = 510(1 + i)40 => i = 6. 11 1955 -1995 (40 years) 6. 11 General inflation rate ~ average rate CPI of items in market basket Specific inflation rate ~ pertains to a segment of the economy CPIk = [(CPI)k - (CPI)k-1](100)/ (CPI)k-1 10/19/2021 rd 7

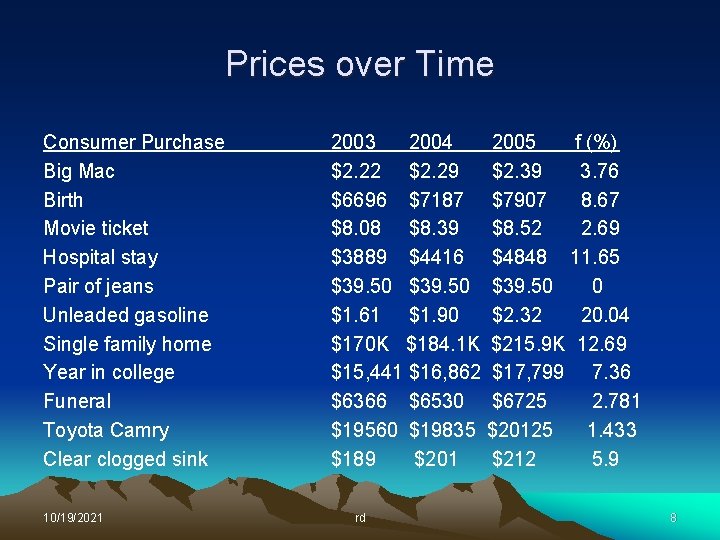
Prices over Time Consumer Purchase Big Mac Birth Movie ticket Hospital stay Pair of jeans Unleaded gasoline Single family home Year in college Funeral Toyota Camry Clear clogged sink 10/19/2021 2003 2004 2005 f (%) $2. 22 $2. 29 $2. 39 3. 76 $6696 $7187 $7907 8. 67 $8. 08 $8. 39 $8. 52 2. 69 $3889 $4416 $4848 11. 65 $39. 50 0 $1. 61 $1. 90 $2. 32 20. 04 $170 K $184. 1 K $215. 9 K 12. 69 $15, 441 $16, 862 $17, 799 7. 36 $6366 $6530 $6725 2. 781 $19560 $19835 $20125 1. 433 $189 $201 $212 5. 9 rd 8

Price Relatives Year 1976 1977 1978 1979 1980 Cost ($) Gallon Price Relatives (Base 1976 =100) 0. 58 100 0. 63 (0. 63/0. 58)(100) = 109 0. 68 (0. 68/0. 58)(100) = 117 0. 93 (0. 93/0. 58)(100) = 160 1. 20 (1. 20/0. 58)(100) = 207 Price Relative in Period t = Price in Period t (100) Base Period Price CPI 1980 = 1. 20 * 100 / 0. 58 = 206. 9 = {[(1. 2 – 0. 58) / 0. 58 ] + 1} * 100 CPI measures changes in food, shelter, medical care, transportation, apparel, and other selected goods and services used by us. No VCRs in 1970 is an example that the CPI Basket has to change. 10/19/2021 rd 9

CPI Overstates Inflation The CPI does not allow for a substitution effect. When the price of soda rises, consumers may switch to water, Snapple, or milk. The CPI market basket is fixed, so it misses this substitution effect. The CPI does not measure quality changes. Cars are more expensive today than in 1980, but they are also safer, more mechanically reliable, pollute less and use less gasoline. The CPI attempts to adjust for quality changes but does so imperfectly, and with a time lag. Some 2008 vehicles are cheaper than 2007. COLAs are then higher than inflation. 10/19/2021 rd 10

How Inflation Works Pay for work = $10/hour Price of bread = $1/loaf One year later Pay for work = $11/hour Price of bread = $1. 10/loaf ~ a 10% increase Conclude: Still can only buy 10 loaves of bread. Are you better off? Keeping pace with inflation? Demand-pull inflation ~ Too many dollars chasing too few goods. Cost-push inflation ~ price hikes like oil. 10/19/2021 rd 11

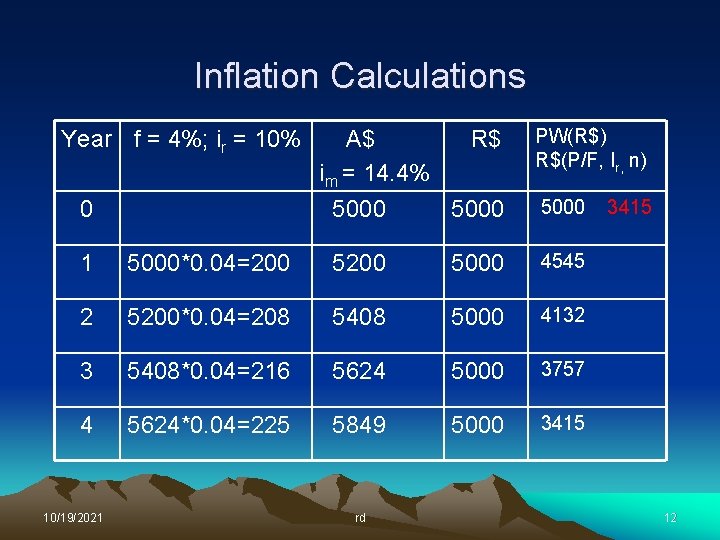
Inflation Calculations Year f = 4%; ir = 10% 0 A$ R$ im = 14. 4% 5000 PW(R$) R$(P/F, Ir, n) 5000 1 5000*0. 04=200 5000 4545 2 5200*0. 04=208 5408 5000 4132 3 5408*0. 04=216 5624 5000 3757 4 5624*0. 04=225 5849 5000 3415 10/19/2021 rd 3415 12

Gain in Purchasing Power Suppose you want a real return (ir) of 4% on $1000 investment for one year with inflation f at 10%. Compute Fat one year. F = 1000(1 + f) = 1 K(1. 1) = $1100 to keep pace with inflation. F = 1000(1 + f)(1 + 0. 04) = $1144. (1 + f)(1 + r) = [1 + f + r + fr] = 1 + m Thus (1 + market rate) = (1 + inflation)(1 + real) (1 + im) = (1 + f)(1 + ir) => im = (1 + f)(1 + ir) – 1 = 1. 1 * 1. 04 – 1 = 14. 4% im = f + ir + f * ir = 0. 1 + 0. 04 + 0. 1* 0. 04 = 14. 4% 10/19/2021 rd 13

Real Interest Rate im = (1 + f)(1 + ir) – 1 ir = 10/19/2021 rd 14

Example 1 Given P = $3000; F = $5000, N = 5 years, f = 5%: Find the market Ro. R and the real rate of return. Method I: 5/3 = (1 + im)5 => im = 10. 76% ir = (1 + im)/(1 + f) – 1 = 1. 1076/1. 05 - 1 = 5. 49% real interest gain Method II F 5 -real = 5 K(P/F, 5%, 5) = $3917. 63 (IGPFN 3000 3917. 63 5) 5. 49% 10/19/2021 rd 15

Example 2 Given P = -$3000, A = $400, F 4 = $2000, N = 4, f = 5% Find im and ir. PW(im) = -3000 + 400(P/A, im, 4) + 2000(P/F, im, 4) = 0 (IRR ‘(-3000 400 400 2400)) 5. 677% => im = 5. 68% (UIRR 3000 4 2000) 5. 68% Adjusting the cash flow each year for inflation, (IRR ‘(-3000 380. 95 362. 81 345. 54 1974. 49)) 0. 65% ir = 0. 65% at base year 0. 10/19/2021 rd 16

Jack vs. Phil Nicklaus won the Masters for $20 K in 1963; Mickelson in 2004 for $1. 17 M. Use CPI of 91. 7 in 1963 and 561. 23 in 2004. Average inflation is 4. 517% = (IGPFN 91. 7 561. 23 41) 20 K(1. 04517)41 = $122, 405. 67 << $1. 17 M, but Jack had 41 years to invest his money. 10/19/2021 rd 17

Example 3 First Cost AOC A $600 K 30 K B N = 20 years $1000 K 10 K a) No inflation B – A: 400 = 20(P/A, im, 20) => im = 0% Select A for any positive MARR. b) Assume inflation f at 5% per year. Select A. 10/19/2021 rd 18

Example 4 You borrow $100 K today to repay in 3 years at im = 11%. Find A$ after 3 years, ir and R$ equivalent to purchasing power with f = 5%. (A$)3 = 100 K(F/P, 11%, 3) = $136, 763. 10 ir = 5. 714% = (1 + im)/(1 + f) - 1 (R$)3 = 100 K(1. 05714)3 = $118, 140. 15 = 100 K(F/P, 11%, 3)(P/F, 5%, 3) = $118, 140. 15 10/19/2021 rd 19

Fixed vs. Responsive Annuity Fixed n 1 2 3 4 … 10/19/2021 A$ 2000 … R$ 1887 1780 1679 1584 … f = 6% Responsive A$ R$ 2120 2000 2247 2000 2382 2000 2525 2000 … … rd 20

Example A company borrows $100, 000 today to repay at the end of 3 years at a market rate im = 11%. Compute the A$ owed at the end of 3 years, the actual and real rate of return to the lender, and the R$ at the end of the third year with inflation f at 5% per year. (A$) = 100, 000(F/P, 11%, 3) = (R$) = 100, 000(F/P, 5. 714%, 3) = $136, 763. 10. $118, 141. 11 IRR (actual) = 11% vs. IRR(real) = (0. 11 - 0. 05) / 1. 05 = 5. 714% = ir. Note that $136, 763(P/F, 5%, 3) = $118, 140. 15 10/19/2021 rd 21

Bond Rate You want to buy a $1000 par-value bond at 9. 5% annual coupon rate with inflation at 4%. Compute your real rate of return if you sell the bond for $1080 after 2 years. n 0 1 2 cf -1000 95 1175 (IRR '(-1000 95 1175)) 13. 25% is the market rate Ro. R. (UIRR 1000 95 2 1080) 13. 251436% Find the real Ro. R with f = 4%. (IRR '(-1000 91. 36 1086. 35)) 8. 8961679% = ir or use f = 4 and im = 13. 25%. 10/19/2021 rd 22

Problem 14 -11 In last 5 years prices have increased a total of 50%. Find f. F = P(1 + i)n 1. 5 = 1(1 + f)5 => f = 8. 4472% 10/19/2021 rd 23

Problem 14 -15 Sally loaned a friend $10 K at 15%/yr to be repaid in 5 uniform payments. Inflation f = 12%. Compute Sally's real Ro. R with this inflation rate. A = 10 K(A/P, 15%, 5) = $2983. 16 (UIRR 10 e 3 2983. 16 5) 15% = im Use f and im to get ir = 2. 6786% (UIRR 10 e 3 2163. 55 5) 2. 6786% where 2163. 55 = 10 K(A/P, 2. 6786%, 5) 10/19/2021 rd 24

Problem 14 -21 With inflation at 6%/yr, how long in years for the purchasing power to be 1/5 of the present value? 1 = (1/5)(1 + 0. 06)n (NGPFI 1/5 1 6) 27. 62 years 10/19/2021 rd 25

Problem 14 -23 Sal invests in a lot for $18 K for 10 years seeking an ir = 10% After Tax Ro. R. f = 6% and the capital gains tax rate is 15%. Find Sal’s selling price. Let x = selling price. Sal pay 15% of (X – 18 K) = 0. 15 X - 2700 n BTCF TI 15%Tax Rate ATCF 0 -18 K 10 X (X – 18 K) -0. 15 X + 2700 0. 85 X + 2700 im = (ir + f + ir * f) in percent = 16. 6% 18 K = (0. 85 X + 2700)(P/F, 16. 6%, 10) => X = $95, 188. 19; or 18 K(F/P, 16. 6%, 10) = 0. 85 X + 2700 => X = $95, 188. 19 10/19/2021 rd 26

Problem 14 -36 Year PSI Change in PSI 1991 82 3. 22% 1992 89 8. 50 1993 100 a a = (100 -89)/89 = 12. 36% 1994 b 4. 00 (b-100)100 = 0. 04; b = 104 1995 107 c (107 -104)/104 = c = 2. 88% 1996 116 d 9/107 = d = 8. 41% 1997 e 5. 17 (e-116)/116 = 5. 17 => e = 122 1998 132 7. 58 b) Base year is 1993 where PSI = 100 c) 1991 -1995 107/82 = (1 + f)4 => f = 6. 88% 1992 -1998 132/89 = (1 + f)6 => f = 6. 79% 10/19/2021 rd 27

Problem 14 -37 n Cost 1 st Mail LCI 1970 $0. 06 100 … … … 1979 0. 15 250 = 100 (1 + f)9 => i = 10. 72% (IGPFN 100 250 9) 10. 72% 10/19/2021 rd 28

Problem 14 -41 Ten years ago the EAT index was 330 and averaged an increase of 12%/year, calculate current value of index. CI= 330(1. 12)10 = 1024. 93 10/19/2021 rd 29

Problem 14 -42 Item Cost now Year 1 Year 2 Year 3 $120 K 4. 3% 3. 2% 6. 6% Roofing 140 K 2. 0 2. 5 3. 0 Heating 35 K 1. 6 2. 1 3. 6 9 K 5. 8 6. 0 7. 5 85 K 5. 0 4. 5 Structural Insulation Labor Im = 25% Find labor costs for years 1 -3. 85 K(1. 05) = $89, 250, 93, 266. 25; 97, 463. 23 Average % increase for labor (IGPFN 85 97. 46323 3) 4. 67% Find PW(insulation) = $9 K Find future worth of insulation and labor Insulation = 9 K(1. 058)(1. 06)(1. 075) = $10, 850. 32 vs. $17, 578. 13 at 25% Labor = 97, 463. 23 => Future cost of (Labor + Insulation) = $108, 313. 55 Future worth 94 K(F/P, 25%, 3) = $183, 593. 75 10/19/2021 rd 30

Problem 14 -50 Tom bought a $10 K 5 -year bond with coupon rate of 12%/year. Tax rate is 42% with inflation f = 7% per year. Find his Before Tax Ro. R without inflation. 12% Find AT Ro. R without inflation and with inflation. n BTCF TI Tax ATCF f = 7% 0 -10 K 1 1200 -504 696 650. 47 6. 96% w/o inflation 2 1200 " " " 607. 91 (1– 0. 42)*0. 12 = 6. 96% 3 1200 " " " 568. 14 4 1200 " " " 530. 98 5 1200 " " " 496. 24 5 10 K $7129. 86+ 496. 24 = 74843. 67 Before tax Ro. R is just the 12%. After Tax Ro. R is 696/10 K = 6. 96% With inflation, ir is not positive since the sum is less than $10 K. (IRR '(-10000 650. 47 607. 91 568. 14 530. 98 7483. 67)) -0. 3645% 10/19/2021 rd 31

Problem 14 -55 F = 5% using straight line depreciation, MARR = 7%. n BTCF(A$ 5%) Dep TI 0 1 2 3 -420 200 200 -420 210 220. 50 231. 53 140 140 70 80. 5 91. 53 -17. 5 -20. 125 -22. 88 n BTCF(A$ 5%) Dep TI Tax-25% ATCF(A$) 0 1 2 3 -300 150 150 -300 157. 5 165. 4 173. 6 100 100 57. 5 65. 4 73. 6 Tax-25% ATCF(A$) -14. 4 -16. 4 -18. 41 -$420 192. 5 200. 375 208. 65 -$300 143. 1 149. 0 155. 2 R$ -$420 183. 33 181. 75 180. 24 R$ -$300 136. 3 135. 1 134. 1 A-B: (IRR '(-120 47 46. 1)) 8. 07% > 7% => Choose A. 10/19/2021 rd 32

Deflation or Negative Inflation The deflation rate is 2% per year for the next 5 years. A par value bond of $10 K with an annual coupon rate of 5% is bought and had a real rate of return of 4%. How much was paid for the bond? im = (1 – 0. 02)(1 + 0. 04) - 1 = 1. 92% PW = 500(P/A, 1. 92%, 5) + 10 K(P/F, 1. 92%, 5) = $11, 455. 12 (IRR '(-11455. 12 500 500 10500)) 1. 92% (UIRR 11455. 12 500 5 10000) 1. 92% 10/19/2021 rd 33

Deflation In 1993 the semiconductor producer price index was 141. 9 and today is 69. 5. Compute the average rate of deflation. 69. 5 = 141. 9(1 + f)14 => f = -5. 231% => deflation. 10/19/2021 rd 34

Example An engineer earns $50 K now with a 4. 3% annual increase. Inflation is at 2. 3%. Compute the engineer's actual dollars over the next 5 years. Engineer's A$ A$1 = 50 K(1. 043)0(P/F, 1. 023%, 1) = $48, 875. 86 A$2 = 50 K(1. 043)1(P/F, 1. 023%, 2) = $49, 831. 40 A$3 = 50 K(1. 043)2(P/F, 1. 023%, 3) = $50, 805. 62 A$4 = 50 K(1. 043)3(P/F, 1. 023%, 4) = $51, 798. 88 A$5 = 50 K(1. 043)4(P/F, 1. 023%, 5) = $52, 811. 57 Real rate of annual increase is not 4. 3%, but 1. 95%. 10/19/2021 rd 35

Exchange Rate The exchange rate for a European firm in 2007 was 0. 6868 euro to purchase $1 US. Suppose a contract showed that a US company was to receive 11 M Euros being earned equal payments quarterly over 1 and ½ years with an increase of 0. 125% per quarter in the exchange rate. Show payments to US firm. 11 M(A/P, 0. 125%, 6) = 1, 841, 362. 52 euro A 1 = 1. 841 M(P/F, 0. 125%, 1) / 0. 6868 = $2, 684, 427 A 2 = 1. 841 M(P/F, 0. 125%, 2) / 0. 6868 = $2, 673, 859 A 3 = 1. 841 M(P/F, 0. 125%, 3) / 0. 6868 = $2, 670, 520 shrinking US A 4 = 1. 841 M(P/F, 0. 125%, 4) / 0. 6868 = $2, 667, 187 dollar A 5 = 1. 841 M(P/F, 0. 125%, 5) / 0. 6868 = $2, 663, 857 A 6 = 1. 841 M(P/F, 0. 125%, 6) / 0. 6868 = $2, 660, 531 Notice shrinking US dollars with time due to increasing exchange rate 10/19/2021 rd 36

Monthly Payment You bought an auto for $25 K to be repaid for 4 years at 12% interest compounded monthly. If general inflation is 6% compounded monthly, find actual and real value of 20 th payment. A$20 = $25 K(A/P, 1%, 48) = $658. 35 R$20 = 658. 35(P/F, ½%, 20) = $595. 84 10/19/2021 rd 37

Geometric Gradient and Inflation Four payments beginning at $7, 000 at the end of year 1 and growing at the rate of 8% per year with market rate at 13%/year and general inflation at 7%/year. Find the present worth of the series. (PGGG 7000 8 5. 60747 4) $27, 428. 25, where im = 13% and f = 7% yielding ir = 5. 60747%. Note real cash flow is 7000 7560 8165 8818 actual cash flow is 7490 8655 10, 002 11, 559 PW = 7490(1. 13)-1 + … + 11599(1. 13)-4 = $27, 428. 25 10/19/2021 rd 38

Monthly Payments under Inflation You borrow $20 K at 12% compounded monthly for 5 years. Average monthly general inflation rate is 0. 5%. Determine equivalent equal monthly payment in real dollars. A$ = 20 K(A/P, 1, 60) = $444. 89 R$ = 20 K(A/P, 0. 4975%, 60) = $386. 38 where ir = 0. 4975%. 10/19/2021 rd 39

Inflation 1. A machine costing $2550 4 years ago now costs $3930 with general inflation at 7% per year. Calculate the true percentage increase in the cost of the machine. a) 14. 95% b) 54. 12% c) 35. 11% d) 7% e) 17. 58% 2. If you want a 7% inflation-free return on your investment with f = 9% per year, your actual interest rate must be closest to a) 16% b) 20% c) 12% d) 15% e) 14% f) 17% 3. I want $25 K per year forever in R$ when I die for my family. Insurer offers 7% per year while inflation is expected to be 4% per year. First payment is 1 year after my death. How much insurance do I need? a) $867 K b) $357 K c) $625 K d) $841 K e) $750 K 10/19/2021 rd rd 40 40

4. If the market rate is x% when the inflation rate is y% and the real rate of return is z%, what is the market rate if f = z% and ir = y%? a) > x% b) < x% c) same as x% d) cannot determine 5. Your brother needs a $5, 000 loan to go to college. Because of his poverty, he will pay nothing for the next four years. Five years from today he will begin paying you $2500 a year for the next 4 years. The first payment occurs 5 years from today and the total of the four payments will be $10, 000. a. First consider the investment without inflation. If your minimum rate of return is 8%, is this an acceptable investment? F 4 = 5 K(1. 08)4 = $6802. 44 vs. 2500(P/A, 8%, 4) = $8280. 32 YES b. For the same payment schedule but with a 5% rate of inflation, is this an acceptable investment? Note that your brother pays you $2500 a year regardless of the inflation rate. Your real MARR is 8%. i. M = 13. 4% => F 4 = 5 K(1. 134)4 = $8268. 41 vs. 2500(P/A, 13. 4%, 4) = $7374. 80. NO 10/19/2021 rd 41

6. The cost of utilities for a fixed amount of power is shown below. Find the inflation rate for each year and then f-bar for the 3 years. n 0 1 2 3 cost $350 K 374. 5 K 397. 7 421. 6 K 7% 6. 2% 6% F-bar = (IGPFN 350 421. 6 3) 6. 4% 7. Find the present worth of the cash flow in #6 with ir = 5%. PW = 350 + 350(P/A, 5%, 3) = $1303. 137 K 10/19/2021 rd 42

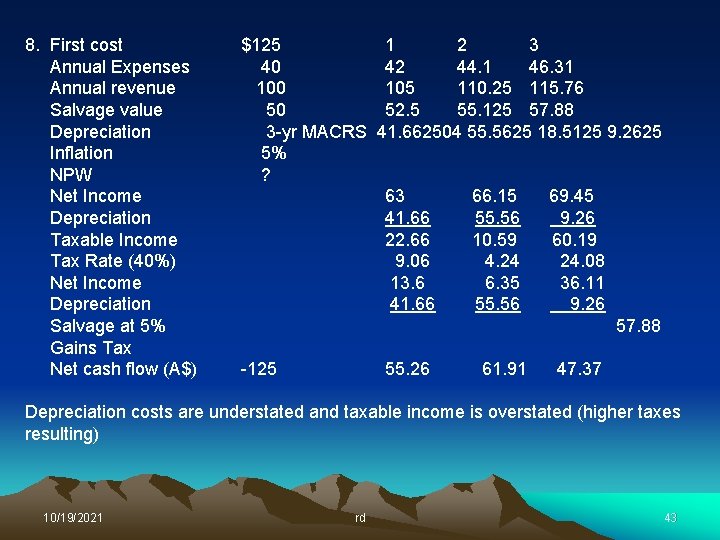
8. First cost Annual Expenses Annual revenue Salvage value Depreciation Inflation NPW Net Income Depreciation Taxable Income Tax Rate (40%) Net Income Depreciation Salvage at 5% Gains Tax Net cash flow (A$) $125 1 2 3 40 42 44. 1 46. 31 100 105 110. 25 115. 76 50 52. 5 55. 125 57. 88 3 -yr MACRS 41. 662504 55. 5625 18. 5125 9. 2625 5% ? 63 66. 15 69. 45 41. 66 55. 56 9. 26 22. 66 10. 59 60. 19 9. 06 4. 24 24. 08 13. 6 6. 35 36. 11 41. 66 55. 56 9. 26 57. 88 -125 55. 26 61. 91 47. 37 Depreciation costs are understated and taxable income is overstated (higher taxes resulting) 10/19/2021 rd 43