Engineering Computation Lecture 5 E T S I

Engineering Computation Lecture 5 E. T. S. I. Caminos, Canales y Puertos 1

Learning Objectives for Lecture 1. Motivate Study of Systems of Equations and particularly Systems of Linear Equations 2. Review steps of Gaussian Elimination 3. Examine how roundoff error can enter and be magnified in Gaussian Elimination 4. Introduce Pivoting and Scaling as defenses against roundoff. 5. Consider what an engineer can do to generate well formulated problems. E. T. S. I. Caminos, Canales y Puertos 2

Systems of Equations • In the previous lecture we have tried to determine the value x, satisfying f(x)=0. In this part we try to obtain the values x 1, x 2, xn, satisfying the system of equations: • These systems can be linear or nonlinear, but in this part we deal with linear systems: E. T. S. I. Caminos, Canales y Puertos 3

Systems of Equations • • where a and b are constant coefficients, and n is the number of equations. Many of the engineering fundamental equations are based on conservation laws. In mathematical terms, these principles lead to balance or continuity equations relating the system behavior with respect to the amount of the magnitude being modelled and the extrenal stimuli acting on the system. E. T. S. I. Caminos, Canales y Puertos 4

Systems of Equations • Matrices are rectangular sets of elements represented by a single symbol. If the set if horizontal it is called row, and if it is vertical, it is called column. Column 3 Row 2 Column vector Row vector E. T. S. I. Caminos, Canales y Puertos 5

Systems of Equations • There are some special types of matrices: Symmetric matrix Diagonal matrix E. T. S. I. Caminos, Canales y Puertos Identity matrix Upper triangular matrix 6

Systems of Equations Lower triangular matrix Banded matrix Half band width All elements are null with the exception of those in a band centered around the main diagonal. This matrix has a band width of 3 and has the name of tridiagonal. E. T. S. I. Caminos, Canales y Puertos 7

Systems of Equations Linear Algebraic Equations a 11 x 1 + a 12 x 2 + a 13 x 3 + … + a 1 nxn = b 1 a 21 x 1 + a 22 x 2 + a 23 x 3 + … + a 2 nxn = b 2 …. . an 1 x 1 + an 2 x 2 + an 3 x 3 + … + anxn = bn where all aij's and bi's are constants. In matrix form: nxn or simply [A]{x} = {b} E. T. S. I. Caminos, Canales y Puertos nx 1 8

Systems of Equations Matrix product: Resulting dimensions • Matrix representation of a system E. T. S. I. Caminos, Canales y Puertos 9

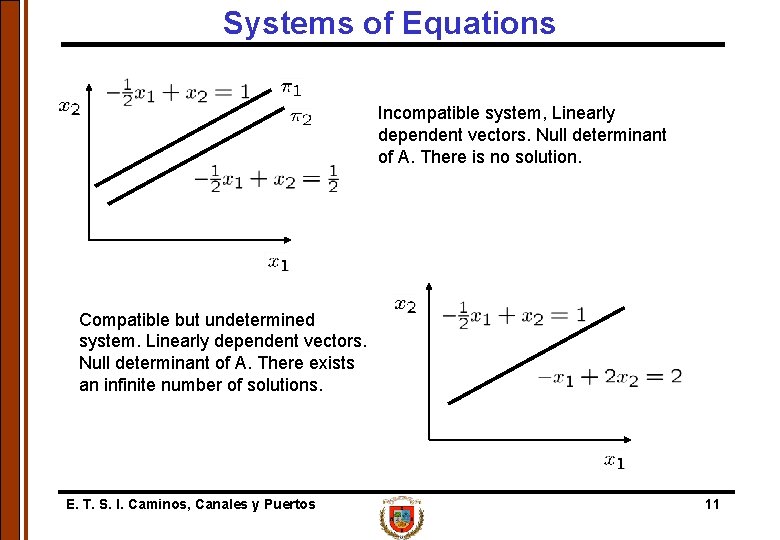
Systems of Equations • Graphic Solution: Systems of equations are hyperplanes (straight lines, planes, etc. ). The solution of a system is the intersection of these hyperplanes. Compatible and determined system. Vectors are linearly independent. Unique solution. Determinant of A is non-null. E. T. S. I. Caminos, Canales y Puertos 10

Systems of Equations Incompatible system, Linearly dependent vectors. Null determinant of A. There is no solution. Compatible but undetermined system. Linearly dependent vectors. Null determinant of A. There exists an infinite number of solutions. E. T. S. I. Caminos, Canales y Puertos 11

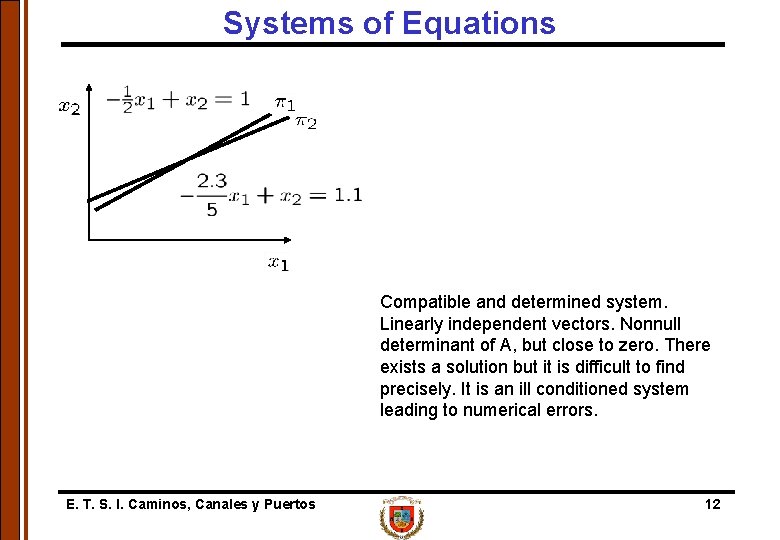
Systems of Equations Compatible and determined system. Linearly independent vectors. Nonnull determinant of A, but close to zero. There exists a solution but it is difficult to find precisely. It is an ill conditioned system leading to numerical errors. E. T. S. I. Caminos, Canales y Puertos 12

Gauss elimination • Naive Gauss elimination method: The Gauss’ method has two phases: Forward elimination and backsustitution. In the first, the system is reduced to an upper triangular system: Pivot equation substract pivot • First, the unknown x 1 is eliminated. To this end, the first row is multiplied by a 21/a 11 and added to the second row. The same is done with all other succesive rows (n-1 times) until only the first equation contains the first unknown x 1. E. T. S. I. Caminos, Canales y Puertos 13

Gauss elimination • This operation is repeated with all variables xi, until an upper triangular matrix is obtained. • Next, the system is solved by backsustitution. • The number of operations (FLOPS) used in the Gauss method is: Pass 1 E. T. S. I. Caminos, Canales y Puertos Pass 2 14

Gauss elimination 1. Forward Elimination (Row Manipulation): a. Form augmented matrix [A|b]: b. By elementary row manipulations, reduce [A|b] to [U|b'] where U is an upper triangular matrix: DO i = 1 to n-1 DO k = i+1 to n Row(k) = Row(k) - (aki/aii)*Row(i) ENDDO E. T. S. I. Caminos, Canales y Puertos 15

Gauss elimination 2. Back Substitution Solve the upper triangular system [U]{x} = {b´} xn = b'n / unn DO i = n-1 to 1 by (-1) END E. T. S. I. Caminos, Canales y Puertos 16

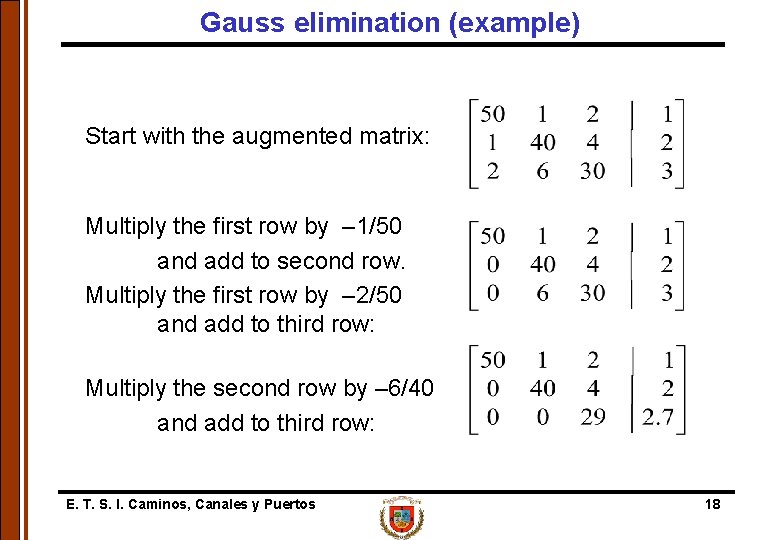
Gauss elimination (example) Consider the system of equations To 2 significant figures, the exact solution is: We will use 2 decimal digit arithmetic with rounding. E. T. S. I. Caminos, Canales y Puertos 17

Gauss elimination (example) Start with the augmented matrix: Multiply the first row by – 1/50 and add to second row. Multiply the first row by – 2/50 and add to third row: Multiply the second row by – 6/40 and add to third row: E. T. S. I. Caminos, Canales y Puertos 18

Gauss elimination (example) Now backsolve: (vs. 0. 091, et = 2. 2%) (vs. 0. 041, et = 2. 5%) (vs. 0. 016, et = 0%) E. T. S. I. Caminos, Canales y Puertos 19

Gauss elimination (example) Consider an alternative solution interchanging rows: After forward elimination, we obtain: Now backsolve: x 3 = 0. 095 x 2 = 0. 020 x 1 = 0. 000 (vs. 0. 091, et = 4. 4%) (vs. 0. 041, et = 50%) (vs. 0. 016, et = 100%) Apparently, the order of the equations matters! E. T. S. I. Caminos, Canales y Puertos 20

Gauss elimination (example) WHAT HAPPENED? • When we used 50 x 1 + 1 x 2 + 2 x 3 = 1 to solve for x 1, there was little change in other equations. • When we used 2 x 1 + 6 x 2 + 30 x 3 = 3 to solve for x 1 it made BIG changes in the other equations. Some coefficients for other equations were lost! The second equation has little to do with x 1. It has mainly to do with x 3. As a result we obtained LARGE numbers in the table, significant roundoff error occurred and information was lost. Things didn't go well! • If scaling factors | aji / aii | are 1 then the effect of roundoff errors is diminished. E. T. S. I. Caminos, Canales y Puertos 21

Gauss elimination (example) Effect of diagonal dominance: As a first approximation roots are: xi bi / aii Consider the previous examples: E. T. S. I. Caminos, Canales y Puertos 22

Gauss elimination (example) Goals: 1. Best accuracy (i. e. minimize error) 2. Parsimony (i. e. minimize effort) Possible Problems: A. Zero on diagonal term ÷ by zero. B. Many floating point operations (flops) cause numerical precision problems and propagation of errors. C. System may be ill-conditioned: det[A] 0. D. No solution or an infinite # of solutions: det[A] = 0. Possible Remedies: A. Carry more significant figures (double precision). B. Pivot when the diagonal is close to zero. C. Scale to reduce round-off error. E. T. S. I. Caminos, Canales y Puertos 23

Gauss elimination (pivoting) PIVOTING A. Row pivoting (Partial Pivoting) In any good routine, at each step i, find maxk | aki | for k = i, i+1, i+2, . . . , n Move corresponding row to pivot position. (i) Avoids zero aii (ii) Keeps numbers small & minimizes round-off, (iii) Uses an equation with large | aki | to find xi · Maintains diagonal dominance. · Row pivoting does not affect the order of the variables. · Included in any good Gaussian Elimination routine. E. T. S. I. Caminos, Canales y Puertos 24

Gauss elimination (pivoting) B. Column pivoting Reorder remaining variables xj for j = i, . . . , n so get largest | aji | Column pivoting changes the order of the unknowns, xi, and thus leads to complexity in the algorithm. Not usually done. C. Complete or Full pivoting Performing both row pivoting and column pivoting. (If [A] is symmetric, needed to preserve symmetry. ) E. T. S. I. Caminos, Canales y Puertos 25

Gauss elimination (pivoting) How to fool pivoting: Multiply the third equation by 100 and then performing pivoting will yield: Forward elimination then yields (2 -digit arithmetic): Backsolution yields: x 3 = 0. 095 (vs. 0. 091, et = 4. 4%) x 2 = 0. 020 (vs. 0. 041, et = 50. 0%) x 1 = 0. 000 (vs. 0. 016, et = 100%) The order of the rows is still poor!! E. T. S. I. Caminos, Canales y Puertos 26

Gauss elimination (scaling) SCALING A. Express all equations (and variables) in comparable units so all elements of [A] are about the same size. B. If that fails, and maxj |aij| varies widely across the rows, replace each row i by: aij This makes the largest coefficient |aij| of each equation equal to 1 and the largest element of [A] equal to 1 or -1 NOTE: Routines generally do not scale automatically; scaling can cause round-off error too! SOLUTIONS • Don't actually scale, but use hypothetical scaling factors to determine what pivoting is necessary. • Scale only by powers of 2: no roundoff or division required. E. T. S. I. Caminos, Canales y Puertos 27

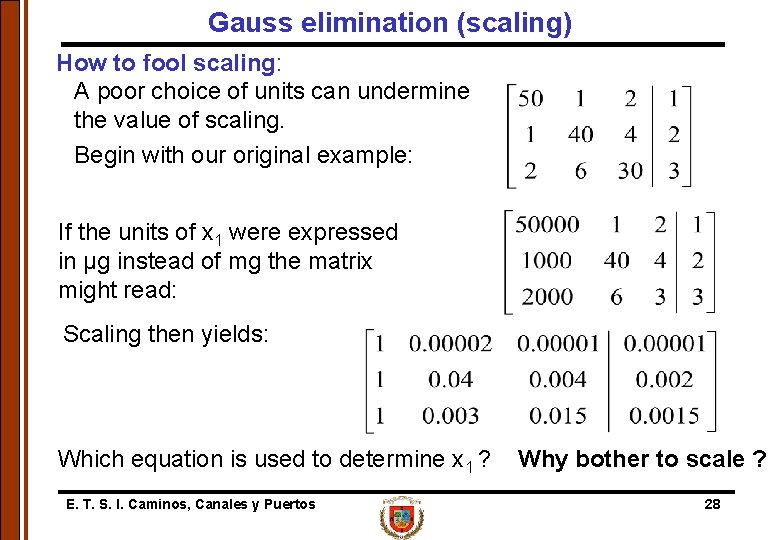
Gauss elimination (scaling) How to fool scaling: A poor choice of units can undermine the value of scaling. Begin with our original example: If the units of x 1 were expressed in µg instead of mg the matrix might read: Scaling then yields: Which equation is used to determine x 1 ? E. T. S. I. Caminos, Canales y Puertos Why bother to scale ? 28

Gauss elimination (operation counting) OPERATION COUNTING In numerical scientific calculations, the number of multiplies & divides often determines CPU time. (This represents the numerical effort!) One floating point multiply or divide (plus any associated adds or subtracts) is called a FLOP. (The adds/subtracts use little time compared to the multiplies/divides. ) FLOP = FLoating point OPeration. Examples: E. T. S. I. Caminos, Canales y Puertos a *x + b a / x – b 29

Gauss elimination (operation counting) Useful identities in counting FLOPS: O(mn) means that there are terms of order mn and lower. E. T. S. I. Caminos, Canales y Puertos 30

Gauss elimination (operation counting) Simple Example of Operation Counting: DO i = 1 to n Y(i) = X(i)/i – 1 ENDDO X(i) and Y(i) are arrays whose values change when i changes. In each iteration X(i)/i – 1 represents one FLOP because it requires one division (& one subtraction). The DO loop extends over i from 1 to n iterations: E. T. S. I. Caminos, Canales y Puertos 31

Gauss elimination (operation counting) Another Example of Operation Counting: DO i = 1 to n Y(i) = X(i) + 1 DO j = i to n Z(j) = [ Y(j) / X(i) ] Y(j) + X(i) ENDDO With nested loops, always start from the innermost loop. [Y(j)/X(i)] * Y(j) + X(i) represents 2 FLOPS E. T. S. I. Caminos, Canales y Puertos 32