Engineering Computation Lecture 2 E T S I

Engineering Computation Lecture 2 E. T. S. I. Caminos, Canales y Puertos 1

Round-off Error due to Arithmetic Operations Smearing Occurs when individual terms are larger than summation itself. Consider the exponential series with x = -10 Consider formulas such as: With 7 -decimal-digit accuracy: exact answer = 4. 54 10 -05 computed answer = – 6. 26 10 -05 (45 terms) wrong sign ! Largest intermediate terms are: 9 th = – 2, 755. 732 & 10 th = 2, 755. 732 E. T. S. I. Caminos, Canales y Puertos 2

Truncation Error caused by the nature of the numerical technique employed to approximate the solution. Example: Maclaurin series expansion of ex If we use a truncated version of the series: Then the Truncation Error is: E. T. S. I. Caminos, Canales y Puertos 3

Approximations and Rounding Errors • Precautions: – Sums of large and small numbers: due to equaling the exponent. They are common in sums of infinite series where the individual terms are very small when compared with the accumulated sum. This error can be reduced by summing first the small terms and using double precision. – Cancellation of the subtraction: The subtraction of very similar numbers. – Smearing: The individual terms are larger than the total sum. – Inner products: They are prone to rounding errors. Thus, it is convenient to use double precision in this type of calculations. E. T. S. I. Caminos, Canales y Puertos 4

Error Propagation Errors which appear because we are basing current calculations on previous calculations which also incurred some form of error Stability and Condition Number Numerically Unstable: Computations which are so sensitive to round-off errors that errors grow uncontrollably during calculations. Condition: sensitivity to such uncertainty; "well conditioned" vs. "ill conditioned" Condition Number: measure of the condition; i. e. , extent to which uncertainty in x is amplified by ƒ(x) C. N. 1 ===> "well-conditioned" C. N. >> 1 ===> "ill-conditioned" E. T. S. I. Caminos, Canales y Puertos 5

Taylor Series Expansion Basic Idea: Predict the value of a function, ƒ, at a point xi+1 based on the value of the function and all of its derivatives, ƒ, ƒ', ƒ", … at a neighboring point xi Given xi, ƒ(xi), ƒ'(xi), ƒ"(xi), . . . ƒn+1(xi), we can predict or approximate ƒ(xi+1) E. T. S. I. Caminos, Canales y Puertos 6

Taylor Series Expansion General Form: h = "step size" = xi+1 – xi Rn = remainder to account for all other terms with xi xi+1 = O (hn+1) with x not exactly known "on the order of hn+1 " Note: f(x) must be a function with n+1 continuous derivatives E. T. S. I. Caminos, Canales y Puertos 7

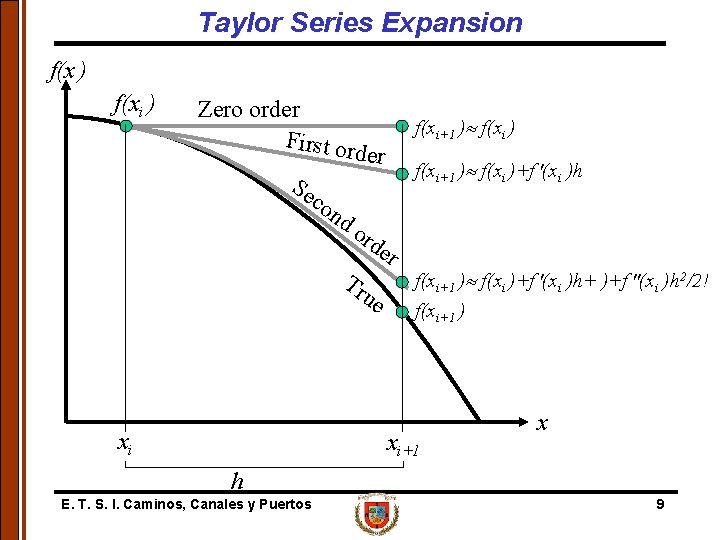
Taylor Series Expansion 0 th order T. S. approx. (n = 0): f(xi+1) = f(xi) + O (h 1) 1 st order T. S. approx. (n = 1): f(xi+1) = f(xi) + hf '(xi) + O (h 2) 2 nd order T. S. approx. (n = 2): nth order T. S. approximation will be exact for an nth order polynomial E. T. S. I. Caminos, Canales y Puertos 8

Taylor Series Expansion f(x ) f(xi ) Zero order First or de f(xi+1 ) f(xi ) r Se f(xi+1 ) f(xi )+f '(xi )h co nd o rd Tr er ue xi f(xi+1 ) f(xi )+f '(xi )h+ )+f "(xi )h 2/2! f(xi+1 ) xi+1 x h E. T. S. I. Caminos, Canales y Puertos 9

Numerical Differentiation from Taylor Series Expansion Objective: Evaluate the derivatives of function, ƒ(xi), without doing it analytically. When would we want to do this? 1. function is too complicated to differentiate analytically: 2. function is not defined by an equation, i. e. , given a set of data points (xi, ƒ(xi)), i=1, …, n i 0 1 2 3 4 xi 1. 0 3. 0 5. 0 7. 0 9. 0 ƒ(xi) 2. 3 4. 1 5. 5 5. 7 5. 9 E. T. S. I. Caminos, Canales y Puertos 10

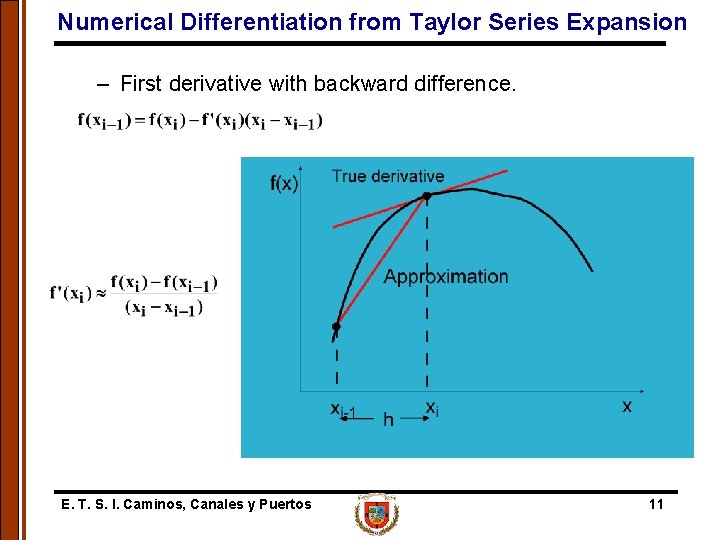
Numerical Differentiation from Taylor Series Expansion – First derivative with backward difference. E. T. S. I. Caminos, Canales y Puertos 11

Numerical Differentiation from Taylor Series Expansion Backward Difference Approx. : First Derivative: Letting h = xi - xi-1 first backward difference E. T. S. I. Caminos, Canales y Puertos 12

Example of 1 st Backward FDD Using data below calculate ƒ'(x 1) : i 0 1 2 3 xi 1. 0 3. 0 5. 0 7. 0 ƒ(xi) 2. 3 4. 1 5. 5 5. 7 4 9. 0 5. 9 First Backward Finite-Divided-Difference at x 1: f ' (x 1) 0. 9 E. T. S. I. Caminos, Canales y Puertos { + O (h) } 13

Backward Difference Approximation Second Derivative: + O([xi-2– xi]3) with h = xi– xi-1 and 2 h = xi – xi-2 The 2 nd order approximation to ƒ(xi-2) becomes: ƒ(xi-2) = ƒ(xi) – 2 hƒ'(xi) + 2 h 2 ƒ"(xi) +O (h 3) [1] 2 nd order approximation to ƒ(xi-1): [2] E. T. S. I. Caminos, Canales y Puertos 14

Backward Difference Approximation Subtracting 2*[2] from [1] yields: f(xi-2) – 2 f(xi-1) = –f(xi) + h 2 f"(xi) + O (h 3) Rearranging: h 2ƒ"(xi) = f(xi) – 2 f(xi-1) + f(xi-2) + O (h 3) Second backward difference E. T. S. I. Caminos, Canales y Puertos 15

Example of 2 nd Backward FDD Using data below calculate ƒ"(x 2) : i 0 1 2 3 xi 1. 0 3. 0 5. 0 7. 0 ƒ(xi) 2. 3 4. 1 5. 5 5. 7 4 9. 0 5. 9 Second Backward Finite-Divided-Difference at x 2: f " (5. 0) - 0. 1 E. T. S. I. Caminos, Canales y Puertos { + O (h) } 16

Other Forms of Numerical Differentiation What points are used for each form? Backward: …, ƒ(xi-2), ƒ(xi-1), ƒ(xi+1), ƒ(xi+2), … Forward: …, ƒ(xi-2), ƒ(xi-1), ƒ(xi+1), ƒ(xi+2), … Centered: …, ƒ(xi-2), ƒ(xi-1), ƒ(xi+1), ƒ(xi+2), … E. T. S. I. Caminos, Canales y Puertos 17

Taylor Series and Truncation errors - Higher order divided differences. - Second finite central divided difference E. T. S. I. Caminos, Canales y Puertos 18

Other Forms of Numerical Differentiation Forward: Centered: E. T. S. I. Caminos, Canales y Puertos 19

Taylor Series and Truncation errors • Use of the Taylor series to calculate derivatives. – First derivative with forward difference. E. T. S. I. Caminos, Canales y Puertos 20

Taylor Series and Truncation errors – First derivative with central differences. E. T. S. I. Caminos, Canales y Puertos 21

Taylor Series and Truncation errors Questions: • Which is a better approximation? Forward, Centered, or Backward? • Why? • When would you use which? Note: We also can get higher order forward, centered, and backward difference derivative approximations [C&C Chapter 23, tabulated in Figs. 23. 1 -3] E. T. S. I. Caminos, Canales y Puertos 22

Example Combining Roundoff and Truncation Error Determine h to minimize the total error of a forward finitedivided difference approximation for: • Truncation Error: xi xi+1 • Round-off Error: with e = machine epsilon. As a result: E. T. S. I. Caminos, Canales y Puertos 23

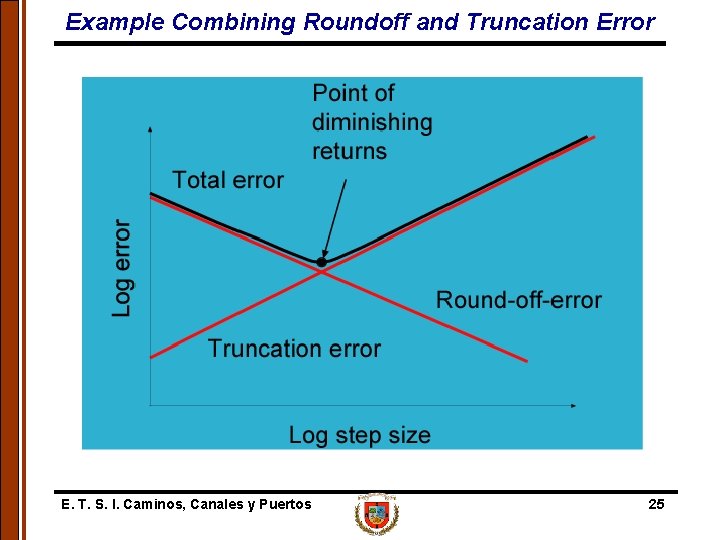
Example Combining Roundoff and Truncation Error Total error = truncation error + roundoff error E = | Total Error | + NOTE: Truncation error decreases as h decreases Round-off error increases as h decreases E. T. S. I. Caminos, Canales y Puertos 24

Example Combining Roundoff and Truncation Error E. T. S. I. Caminos, Canales y Puertos 25

Example Combining Roundoff and Truncation Error To minimize total error E with respect to h, set the first derivative to zero: Solve for h and approximate f "( ) as f "(xi): E. T. S. I. Caminos, Canales y Puertos 26

Example Combining Roundoff and Truncation Error Linear Application: Determine h that will minimize total error for calculating f’(x) for f(x) = x at x=1 Using the first forward-divided-difference approximation with error O(h) and a 5 -decimal-digit machine: e = b 1 -t = 101 -5 = 10 -4 = 0. 0001 f '(x) = ; E. T. S. I. Caminos, Canales y Puertos f "(x) = 0 27

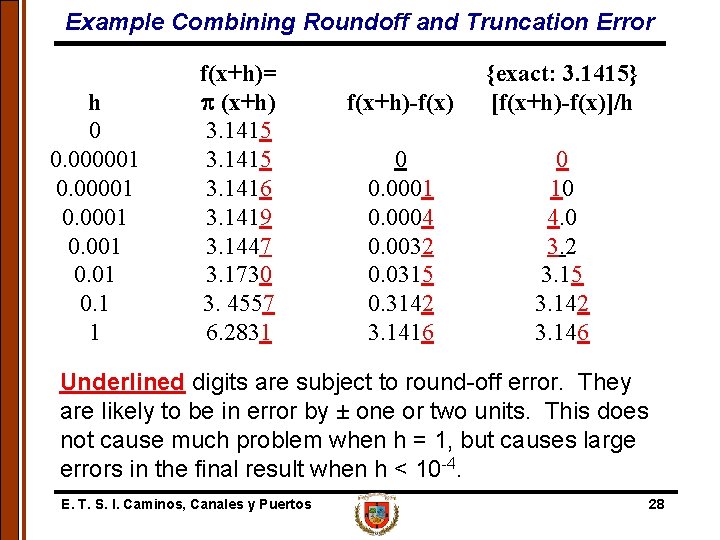
Example Combining Roundoff and Truncation Error h 0 0. 000001 0. 1 1 f(x+h)= (x+h) 3. 1415 3. 1416 3. 1419 3. 1447 3. 1730 3. 4557 6. 2831 f(x+h)-f(x) {exact: 3. 1415} [f(x+h)-f(x)]/h 0 0. 0001 0. 0004 0. 0032 0. 0315 0. 3142 3. 1416 0 10 4. 0 3. 2 3. 15 3. 142 3. 146 Underlined digits are subject to round-off error. They are likely to be in error by ± one or two units. This does not cause much problem when h = 1, but causes large errors in the final result when h < 10 -4. E. T. S. I. Caminos, Canales y Puertos 28

Example Combining Roundoff and Truncation Error Nonlinear Application: Determine h for minimizing the total error for computing f’(x) for ƒ(x) = ex at x=3 Using the first forward-divided-difference approximation with error O(h) and a 5 -decimal-digit machine: e = b 1 -t = 101 -5 = 10 -4 = 0. 0001 f(x) = f '(x) = f "(x) = ex = 20. 0855; or about 0. 01 E. T. S. I. Caminos, Canales y Puertos 29

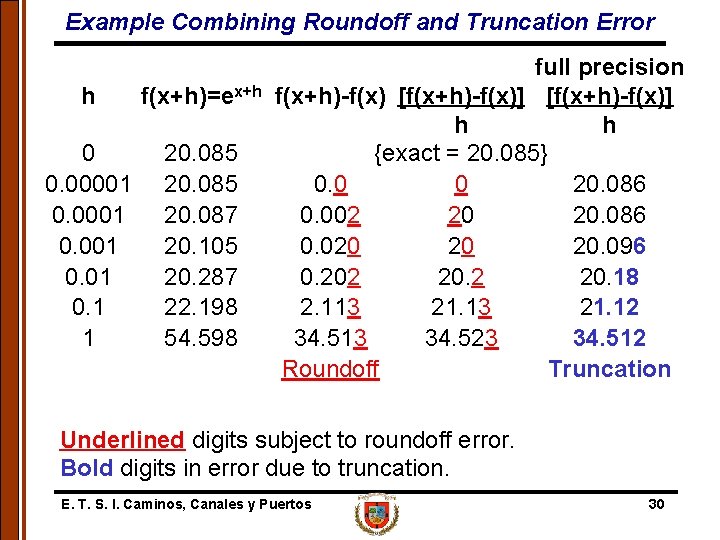
Example Combining Roundoff and Truncation Error h f(x+h)=ex+h 0 0. 00001 0. 1 1 20. 085 20. 087 20. 105 20. 287 22. 198 54. 598 full precision f(x+h)-f(x) [f(x+h)-f(x)] h h {exact = 20. 085} 0. 0 0 20. 086 0. 002 20 20. 086 0. 020 20 20. 096 0. 202 20. 18 2. 113 21. 12 34. 513 34. 523 34. 512 Roundoff Truncation Underlined digits subject to roundoff error. Bold digits in error due to truncation. E. T. S. I. Caminos, Canales y Puertos 30