Engineering a Set Intersection Algorithm for Information Retrieval

Engineering a Set Intersection Algorithm for Information Retrieval Alex Lopez-Ortiz UNB / Inter. NAP Joint work with Ian Munro and Erik Demaine

Overview • • • Web Search Engine Basics Algorithms for set operations Theoretical Analysis Experimental Analysis Engineering an Improved Algorithm Conclusions

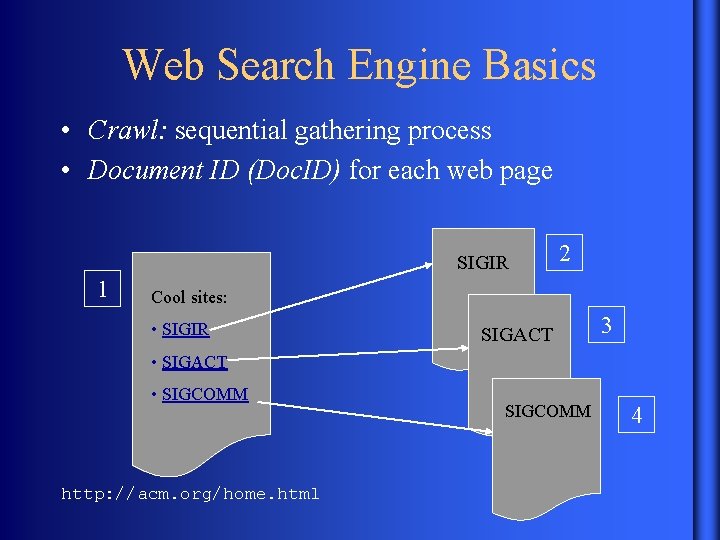
Web Search Engine Basics • Crawl: sequential gathering process • Document ID (Doc. ID) for each web page SIGIR 1 2 Cool sites: • SIGIR SIGACT 3 • SIGACT • SIGCOMM http: //acm. org/home. html SIGCOMM 4

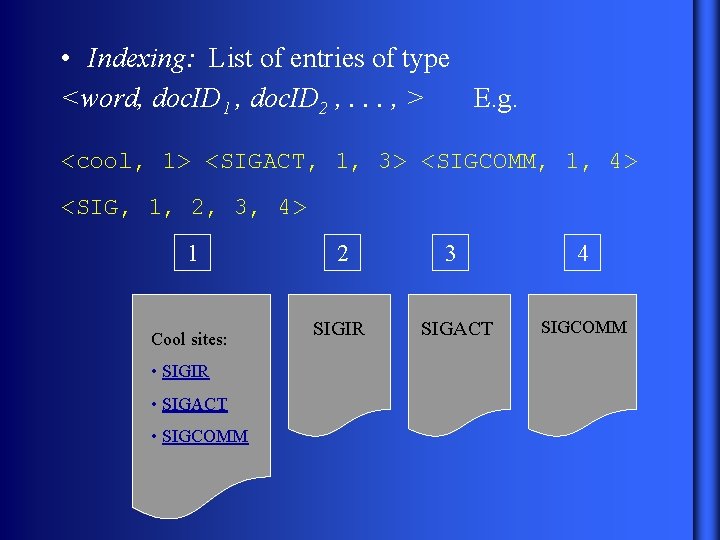
• Indexing: List of entries of type <word, doc. ID 1 , doc. ID 2 , . . . , > E. g. <cool, 1> <SIGACT, 1, 3> <SIGCOMM, 1, 4> <SIG, 1, 2, 3, 4> 1 Cool sites: • SIGIR • SIGACT • SIGCOMM 2 SIGIR 3 SIGACT 4 SIGCOMM

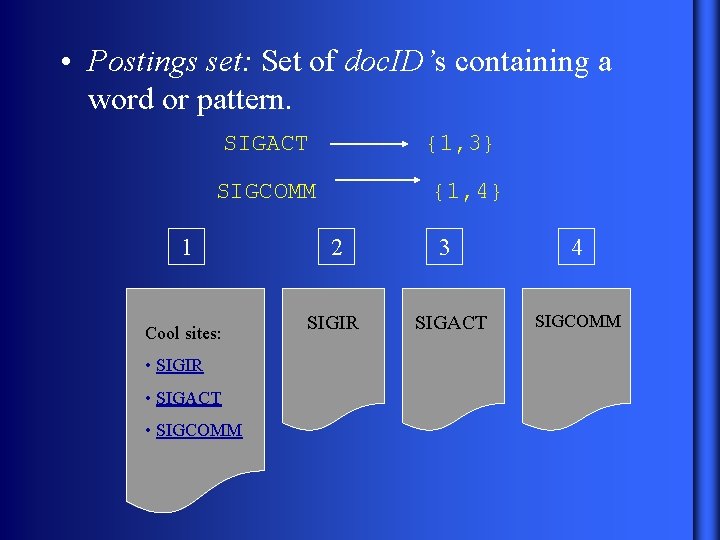
• Postings set: Set of doc. ID’s containing a word or pattern. SIGACT {1, 3} SIGCOMM {1, 4} 1 Cool sites: • SIGIR • SIGACT • SIGCOMM 2 SIGIR 3 SIGACT 4 SIGCOMM

Search Engine Basics (cont. ) Postings set stored implicitly/explicitly in a string matching data structure • • PAT tree/array Inverted word index Suffix trees KMP (grep). . .

String Matching Problem • Different performance characteristics for each solution • Time/Space tradeoff (empirical) • Linear time/linear space lower bound [Demaine/L-O, SODA 2001]

Search Engine Basics (cont. ) A user query is of the form: keyword 1 keyword 2 … keywordn where is one of {and, or} E. g. computer and science or internet

Evaluating a Boolean Query The interpretation of a boolean query is the mapping: • keyword postings set • and (set intersection) • or (set union) E. g. {computer} {science} {internet}

Set Operations for Web Search Engines • Average postings set size > 10 million • Postings set are sorted

Intersection Time Complexity • Worst case linear on size of postings sets: Θ(n) {1, 3, 5, 7} • On size of output? {1, 3, 5, 7} {2, 4, 6, 8}

Adaptive Algorithms • Assume the intersection is empty. What is the min number of comparisons needed to ascertain this fact? Examples {1, 2, 3, 4} {5, 6, 7, 8}

Much ado About Nothing A sequence of comparisons is a proof of non -intersection if every possible instance of sets satisfying said sequence has empty intersection. E. g. A={1, 3, 5, 7} B={2, 4, 6, 8} a 1 < b 1 < a 2 < b 2 < a 3 < b 3 < a 4 < b 4

Adaptive Algorithms In [SODA 2000] we proposed an adaptive algorithm that intersects k sets in: k · | shortest proof of non-intersection | steps. Ideal for crawled, “bursty” data sets

How does it work? • <SIGACT, 1, 3, i, n> 1, _, 3, . . . i n Doc. ID universe set

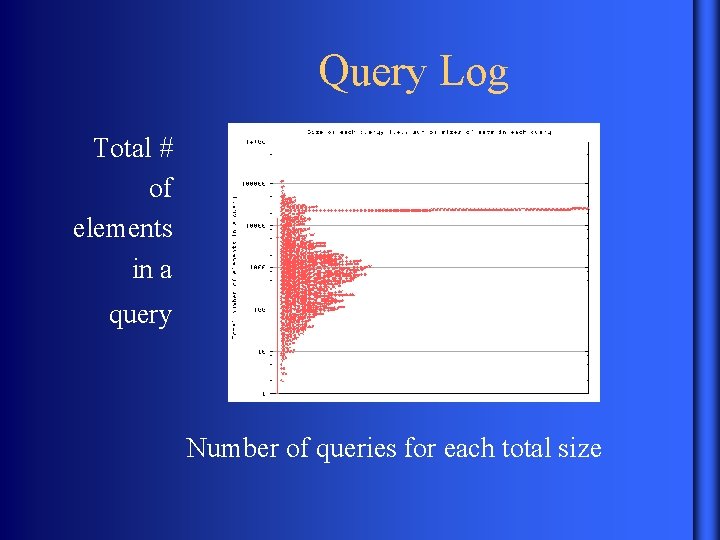
Measuring Performance • 100 MB Web Crawl • 5000 queries from Google

Baseline Standard Algorithm • Sort sets by size • Candidate answer set is smallest set • For each set S in increasing order by size – For each element e in candidate set • Binary search for e in S • If e is not found remove from candidate set • Remove elements before e in S

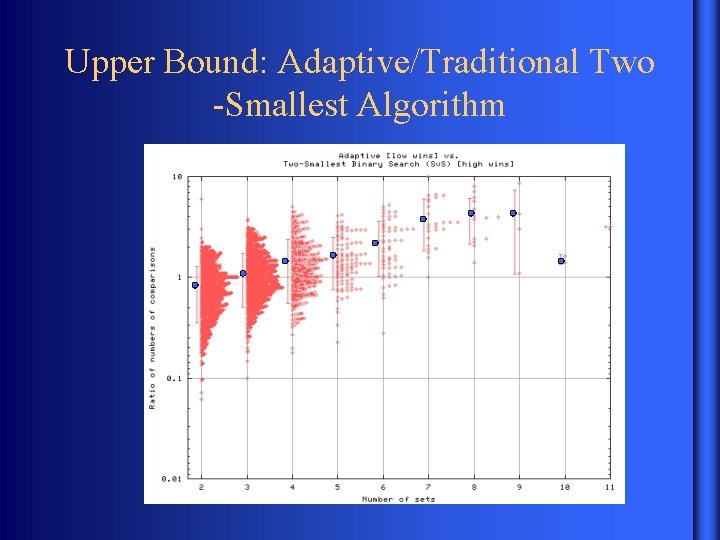
Upper Bound: Adaptive/Traditional Two -Smallest Algorithm

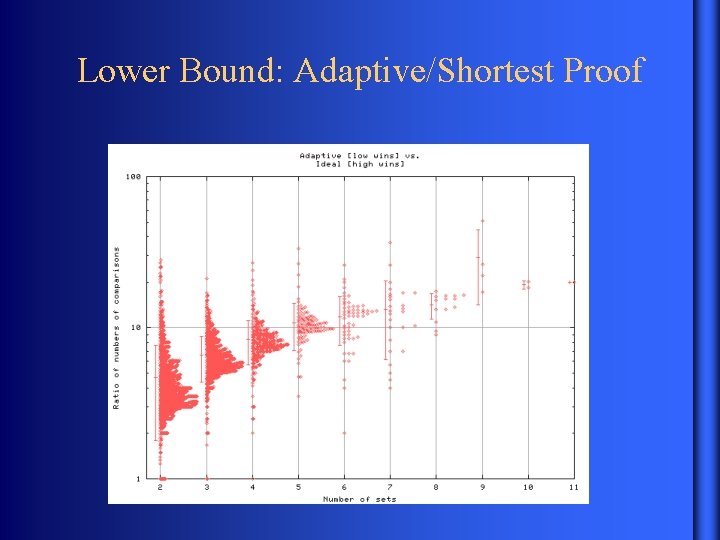
Lower Bound: Adaptive/Shortest Proof

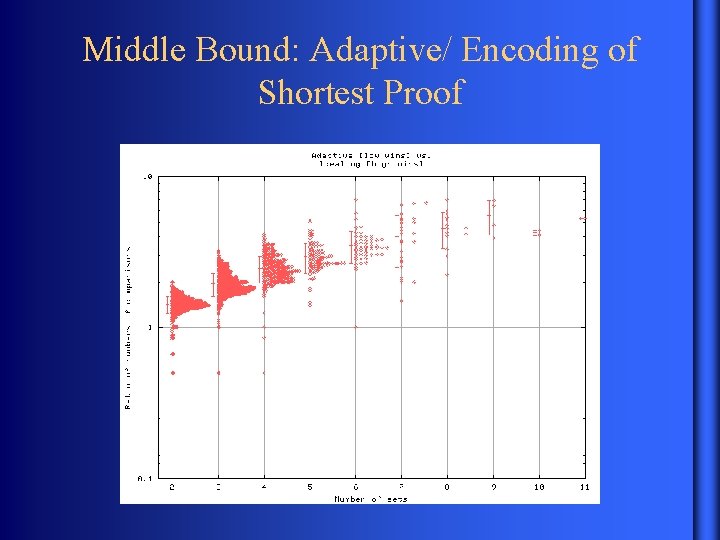
Middle Bound: Adaptive/ Encoding of Shortest Proof

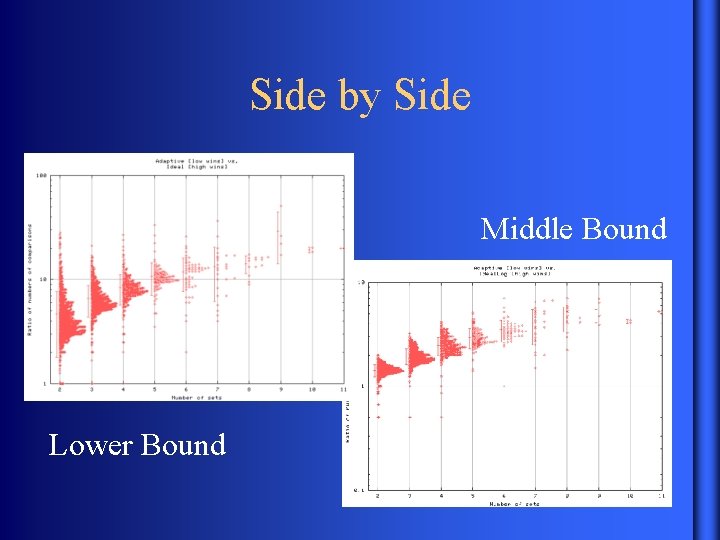
Side by Side Middle Bound Lower Bound

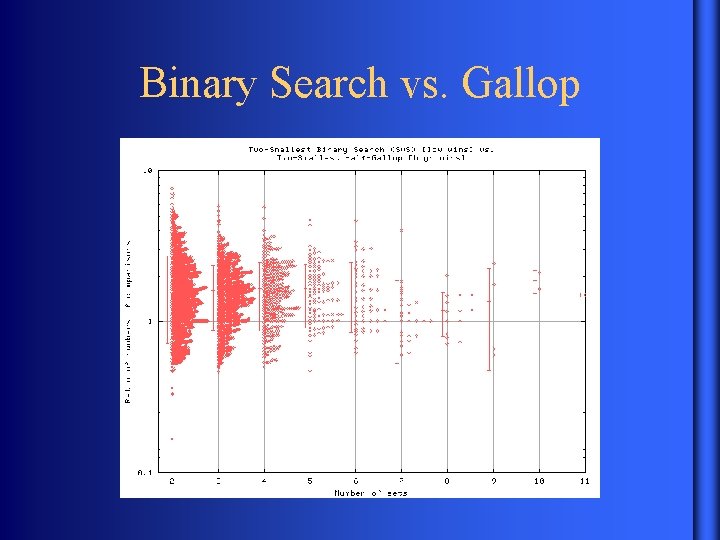
Possible Improvements • Adaptive performs best in two-three sets • Traditional algorithm often terminates after first pair of sets • Galloping seems better than binary search • Adaptive keeps a dynamic definition of “smallest set” • Candidate elements aggressively tested

Example {6, 7, 10, 11, 14} {4, 8, 10, 11, 15} {1, 2, 4, 5, 7, 8, 9}

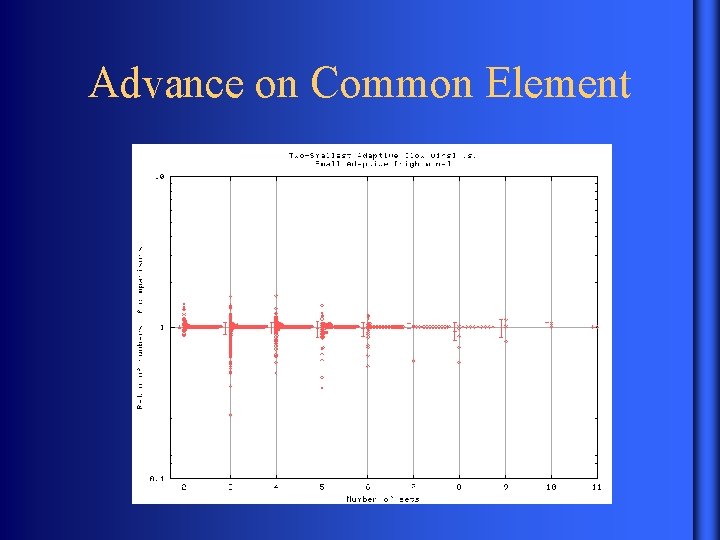
Experimental Results Test orthogonally each possible improvement • Cyclic or Two Smallest • Symmetric • Update Smallest • Advance on Common Element • Gallop Factor/Binary Search

Binary Search vs. Gallop

Advance on Common Element

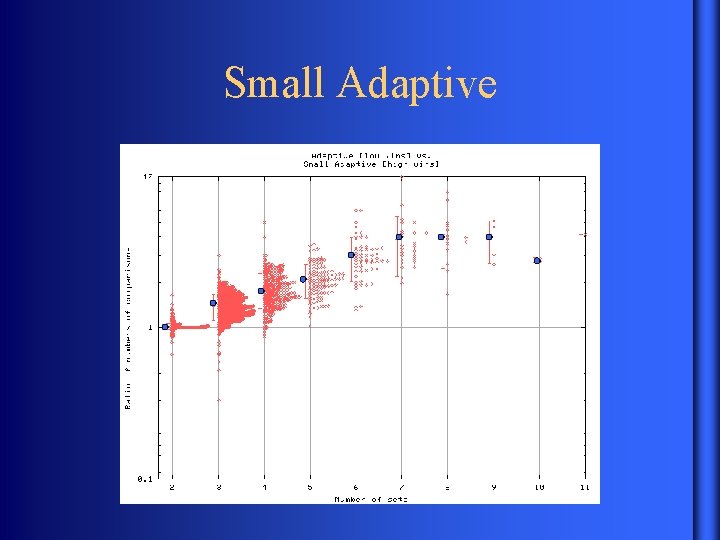
Small Adaptive Combines best of Adaptive and Two-Smallest • Two-smallest • Symmetric • Advance on common element • Update on smallest • Gallop with factor 2

Small Adaptive

Small Adaptive ü Small Adaptive is faster than Two-Smallest üAggregate speed-up 2. 9 x comparisons ü Faster than Adaptive

Conclusions ü Faster intersection algorithm for Web Search Engines ü Adaptive measure for set operations ü Information theoretic “middle bound” ü Standard speed-up techniques for other settings THE END

Query Log Total # of elements in a query Number of queries for each total size

Example {6, 7, 10, 11, 14} {4, 8, 10, 11, 15} {1, 2, 4, 5, 7, 8, 9, 12}