ENGI 1313 Mechanics I Lecture 40 Center of



















- Slides: 27

ENGI 1313 Mechanics I Lecture 40: Center of Gravity, Center of Mass and Geometric Centroid Shawn Kenny, Ph. D. , P. Eng. Assistant Professor Faculty of Engineering and Applied Science Memorial University of Newfoundland spkenny@engr. mun. ca

Material Coverage for Final Exam n n Introduction (Ch. 1: Sections 1. 1– 1. 6) Force Vectors (Ch. 2: Sections 2. 1– 2. 9) Particle Equilibrium (Ch. 3: Sections 3. 1– 3. 4) Force System Resultants (Ch. 4: Sections 4. 1– 4. 10) Ø n n Rigid Body Equilibrium (Ch. 5: Sections 5. 1– 5. 7) Structural Analysis (Ch. 6: Sections 6. 1– 6. 4 & 6. 6) Friction (Ch. 8: Sections 8. 1– 8. 3) Center of Gravity and Centroid (Ch. 9: Sections 9. 1– 9. 3) Ø Ø 2 Omit Wrench (p. 174) Ignore problems involving closed-form integration Simple shapes such as square, rectangle, triangle and circle © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 40

Lecture 40 Objective to understand the concepts of center of gravity, center of mass, and geometric centroid n to be able to determine the location of these points for a system of particles or a body n 3 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 40

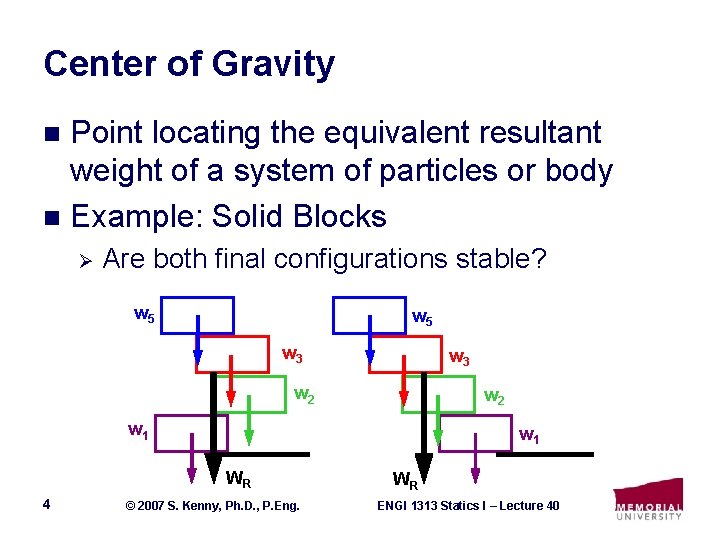
Center of Gravity Point locating the equivalent resultant weight of a system of particles or body n Example: Solid Blocks n Ø Are both final configurations stable? w 5 w 3 w 2 w 1 WR 4 © 2007 S. Kenny, Ph. D. , P. Eng. WR ENGI 1313 Statics I – Lecture 40

Center of Gravity (cont. ) n n Resultant Weight L/2 w 4 Coordinates w 3 z n 5 Key Property © 2007 S. Kenny, Ph. D. , P. Eng. x. G ~ z 1 w 2 w 1 ~ x 1 WR x ENGI 1313 Statics I – Lecture 40

Center of Gravity (cont. ) n Generalized Formulae Moment about y-axis Moment about x-axis ~ z 2 z~n “Moment” about x-axis or y-axis 6 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 40 ~ z 1

Center of Mass n Point locating the equivalent resultant mass of a system of particles or body Generally coincides with center of gravity (G) Ø Center of mass coordinates Ø 7 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 40

Center of Mass (cont. ) n Can the Center of Mass be Outside the Body? Fulcrum / Balance Center of Mass 8 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 40

Center of Gravity & Mass – Applications n Dynamics Inertial terms Ø Vehicle roll-over and stability Ø 9 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 40

Geometric Centroid Point locating the geometric center of an object or body n Homogeneous body n Ø Body with uniform distribution of density or specific weight • Center of mass and center of gravity coincident • Centroid only dependent on body dimensions and not weight terms 10 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 40

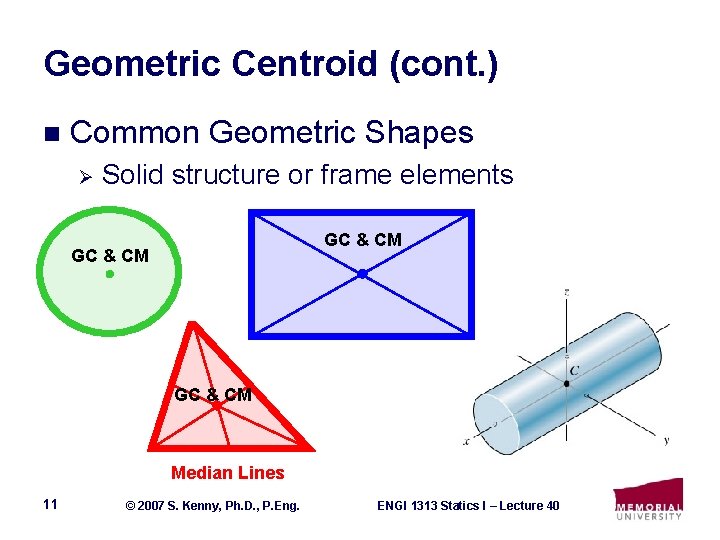
Geometric Centroid (cont. ) n Common Geometric Shapes Ø Solid structure or frame elements GC & CM Median Lines 11 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 40

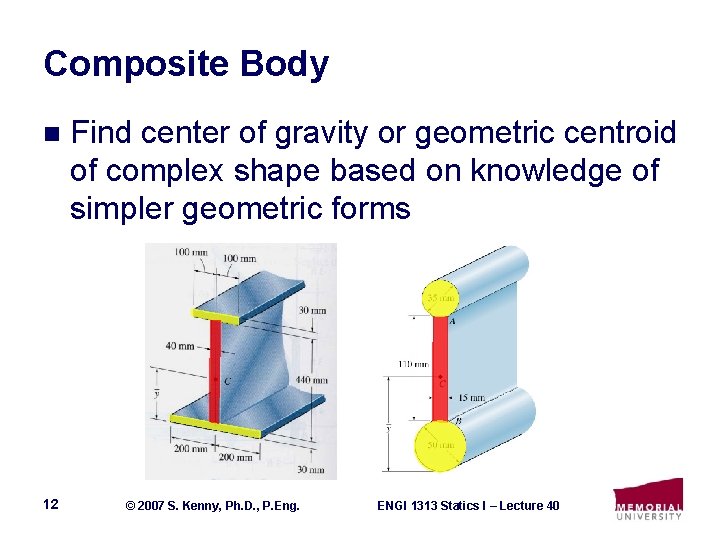
Composite Body n 12 Find center of gravity or geometric centroid of complex shape based on knowledge of simpler geometric forms © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 40

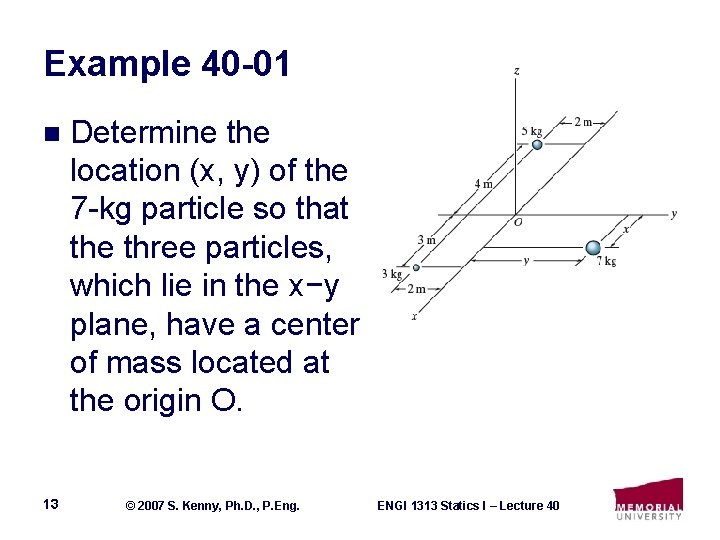
Example 40 -01 n 13 Determine the location (x, y) of the 7 -kg particle so that the three particles, which lie in the x−y plane, have a center of mass located at the origin O. © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 40

Example 40 -01 (cont. ) n 14 Center of Mass © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 40

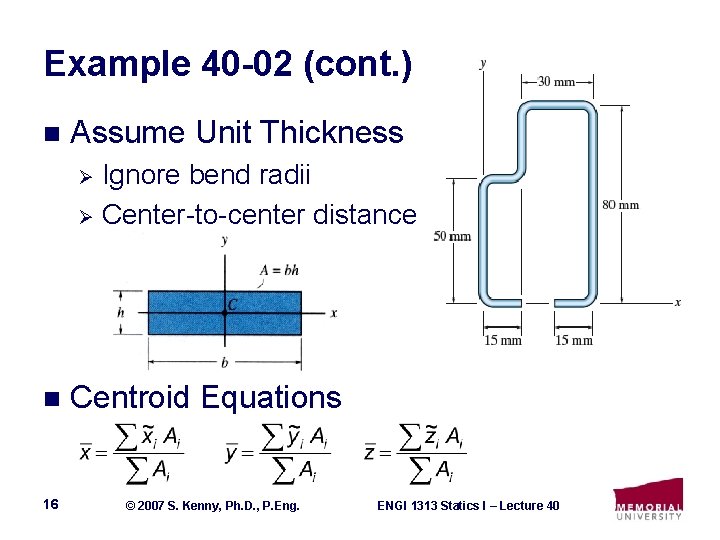
Example 40 -02 n 15 A rack is made from roll -formed sheet steel and has the cross section shown. Determine the location (x, y) of the centroid of the cross section. The dimensions are indicated at the center thickness of each segment. © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 40

Example 40 -02 (cont. ) n Assume Unit Thickness Ignore bend radii Ø Center-to-center distance Ø n 16 Centroid Equations © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 40

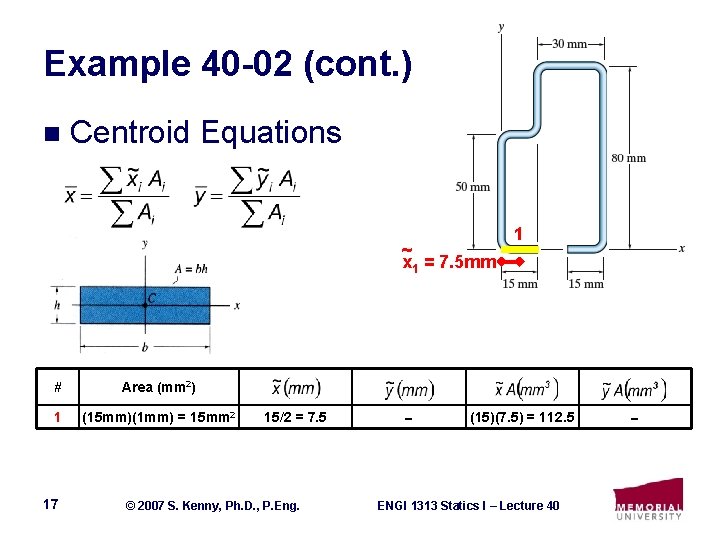
Example 40 -02 (cont. ) n Centroid Equations ~ x 1 = 7. 5 mm # Area (mm 2) 1 (15 mm)(1 mm) = 15 mm 2 17 15/2 = 7. 5 © 2007 S. Kenny, Ph. D. , P. Eng. 1 (15)(7. 5) = 112. 5 ENGI 1313 Statics I – Lecture 40

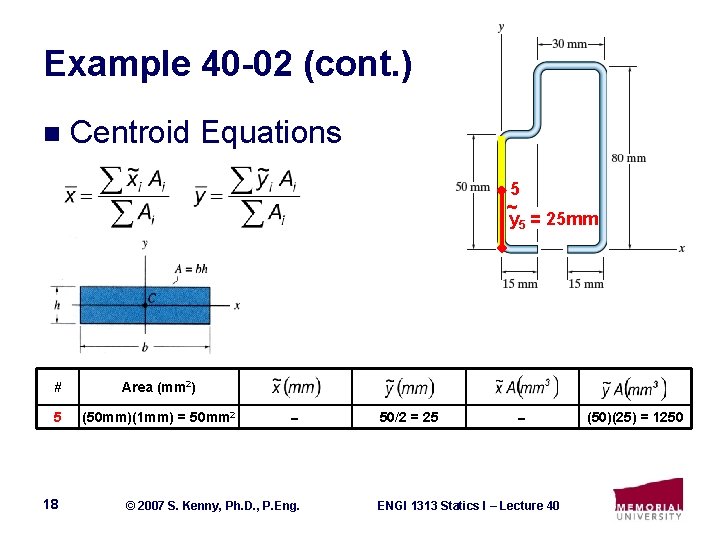
Example 40 -02 (cont. ) n Centroid Equations 5 ~ y 5 = 25 mm # Area (mm 2) 5 (50 mm)(1 mm) = 50 mm 2 18 © 2007 S. Kenny, Ph. D. , P. Eng. 50/2 = 25 ENGI 1313 Statics I – Lecture 40 (50)(25) = 1250

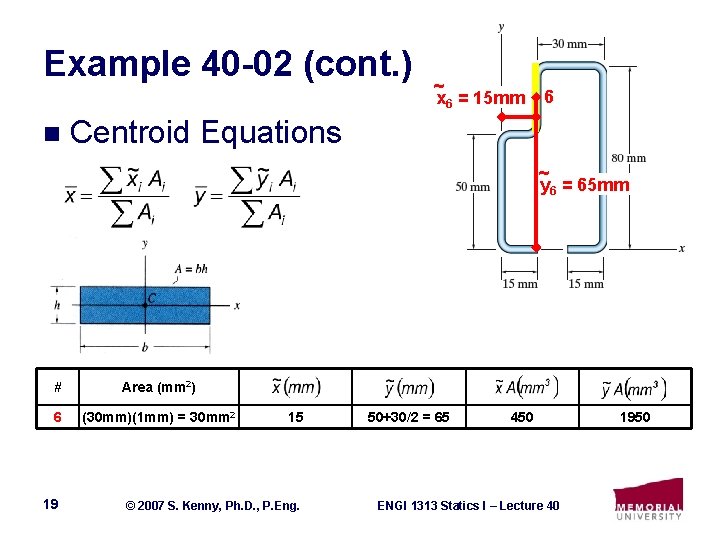
Example 40 -02 (cont. ) n ~ x 6 = 15 mm 6 Centroid Equations ~ y 6 = 65 mm # Area (mm 2) 6 (30 mm)(1 mm) = 30 mm 2 19 15 © 2007 S. Kenny, Ph. D. , P. Eng. 50+30/2 = 65 450 ENGI 1313 Statics I – Lecture 40 1950

4 Example 40 -02 (cont. ) 3 n Centroid Equations 7 5 1 # Area (mm 2) 1 (15 mm)(1 mm) = 15 mm 2 2 112. 5 (15 mm)(1 mm) = 15 mm 2 30+15/2 = 37. 5 562. 5 3 (15 mm)(1 mm) = 15 mm 2 50 112. 5 750 4 (30 mm)(1 mm) = 30 mm 2 15+30/2 = 30 80 900 2400 5 (50 mm)(1 mm) = 50 mm 2 50/2 = 25 1250 6 (30 mm)(1 mm) = 30 mm 2 15 50+30/2 = 65 450 1950 7 (80 mm)(1 mm) = 80 mm 2 45 80/2 = 40 3600 3200 Sum 235 mm 2 20 © 2007 S. Kenny, Ph. D. , P. Eng. 15/2 = 7. 5 6 5737. 5 mm 3 9550 mm 3 ENGI 1313 Statics I – Lecture 40 2

Example 40 -02 (cont. ) n Centroid Equations 24. 4 mm 40. 6 mm 21 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 40

Example 40 -03 n 22 Two blocks of different materials are assembled as shown. The densities of the materials are: A = 150 lb/ft 3 and A = 400 lb/ft 3. The center of gravity of this assembly. © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 40

Example 40 -03 (cont. ) n 23 Center of Gravity © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 40

Example 40 -03 (cont. ) n Center of Gravity # Weight (lb) A 3. 125 4 1 2 12. 5 3. 125 6. 25 B 16. 67 1 3 3 16. 67 50 50 19. 79 29. 17 53. 13 56. 25 24 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 40

Example 40 -03 (cont. ) n 25 Center of Gravity © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 40

Chapter 9 Problems n Understand principles for simple geometric shapes Ø Ø n Review Ø Ø n Example 9. 9 and 9. 10 Problems 9 -44 to 9 -61 Omit Ø Ø 26 Rectangle, square, triangle and circle No closed form integration knowledge required Example 9. 1 through 9. 8 Problems 9 -1 through 9 -43, 9 -62, 9 -67 to 9 -83 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 40

References Hibbeler (2007) n http: //wps. prenhall. com/esm_hibbeler_eng mech_1 n 27 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 40