ENGI 1313 Mechanics I Lecture 12 3 D

ENGI 1313 Mechanics I Lecture 12: 3 D Particle Equilibrium Shawn Kenny, Ph. D. , P. Eng. Assistant Professor Faculty of Engineering and Applied Science Memorial University of Newfoundland spkenny@engr. mun. ca

Chapter 3 Objectives to introduce the concept of the free-body diagram for a particle. n to show to solve particle equilibrium problems using the equations of equilibrium n 2 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 12

Lecture 12 Objectives n 3 to examine and apply Chapter 3 objectives in 3 D space © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 12

Note on Tutorial Problem Set #3 n Revised Problem Set Problem 6 with spring deleted Ø Problem added on Dot Product Ø 4 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 12

Example 12 -01 n 5 A plate with a mass of 150 kg is supported by three cables and is in equilibrium. Find the tension force in each cable. © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 12

Example 12 -01 (cont. ) n What is known? Plate mass Ø Coordinate geometry Ø n What is needed? Convert mass to weight (force) Ø Determine cable forces Ø • Cartesian force vectors ¨ 6 Magnitude, direction and sense © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 12

Example 12 -01 (cont. ) Draw FBD at A n Define Cartesian Force Vectors n FA = W = 150 kg (9. 806 m/s 2) = 1471 N A FAB 7 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 12 FAC FAD

Example 12 -01 (cont. ) n Combine Like Terms Ø x, y and z directions FA = W = 150 kg (9. 806 m/s 2) = 1471 N A FAB 8 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 12 FAC FAD

Example 12 -01 (cont. ) n Multiply Fx by 1. 5 and add to Fy FA = W = 150 kg (9. 806 m/s 2) = 1471 N A FAB 9 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 12 FAC FAD

Example 12 -01 (cont. ) n Multiply Fx by 3 and add to Fz FA = W = 150 kg (9. 806 m/s 2) = 1471 N A FAB 10 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 12 FAC FAD

Pulley Systems n Assumptions Ø In this course for analysis of all pulley systems • • • n Fixed Pulley Ø Class 1 • Ø Ø 11 Weightless Zero friction Tension cables Fixed axle Used to change direction of the pull force Mechanical advantage of 1 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 12

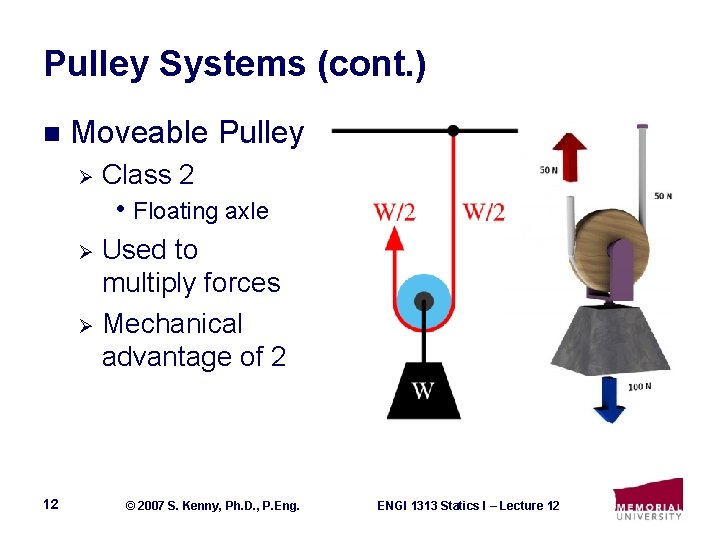
Pulley Systems (cont. ) n Moveable Pulley Ø Class 2 • Floating axle Used to multiply forces Ø Mechanical advantage of 2 Ø 12 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 12

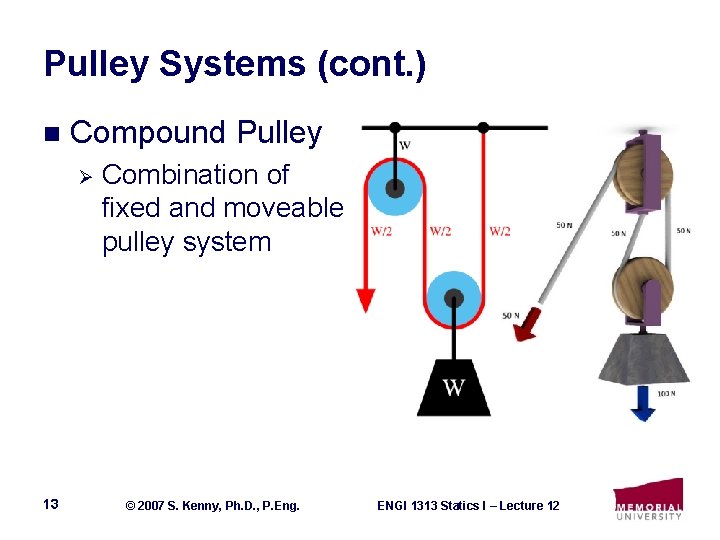
Pulley Systems (cont. ) n Compound Pulley Ø 13 Combination of fixed and moveable pulley system © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 12

Example 12 -02 n 14 D The "scale" consists of a known weight W which is suspended at A from a cord of total length L. Determine the weight w at B if A is at a distance y for equilibrium. Neglect the sizes and weights of the pulleys. © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 12 C

Example 12 -02 (cont. ) n Examine Pulley System Known weight, W 1 Ø Find weight w 2 at B for equilibrium position y D C W 1 Ø W 1 w 2 = ? 15 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 12

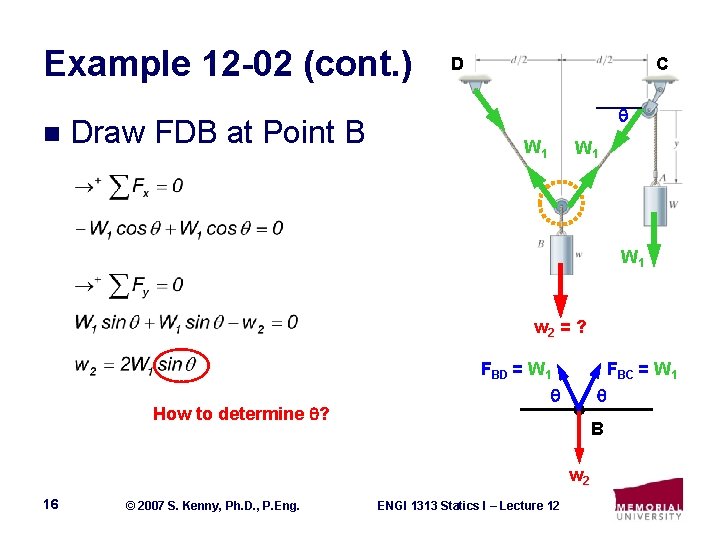
Example 12 -02 (cont. ) n Draw FDB at Point B D C W 1 W 1 w 2 = ? How to determine ? FBD = W 1 FBC = W 1 B w 2 16 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 12

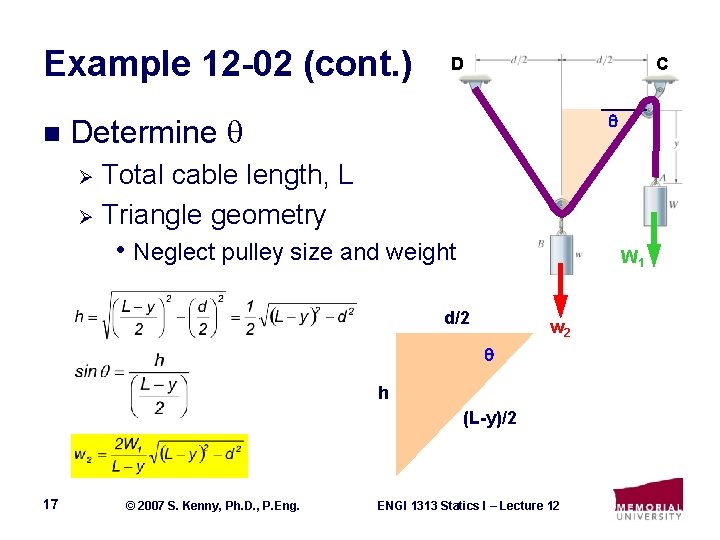
Example 12 -02 (cont. ) n D C Determine Total cable length, L Ø Triangle geometry Ø • Neglect pulley size and weight W 1 d/2 w 2 h (L-y)/2 17 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 12

Example 12 -03 n 18 The joint of a space frame is subjected to four member forces. Member OA lies in the x–y plane and member OB lies in the y–z plane. Determine the forces acting in each of the members required for equilibrium of the joint. © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 12

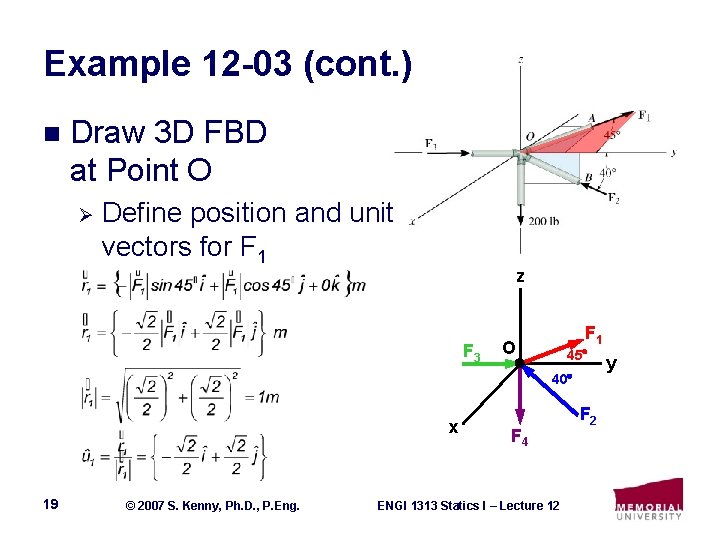
Example 12 -03 (cont. ) n Draw 3 D FBD at Point O Ø Define position and unit vectors for F 1 z F 3 F 1 O 45 40 x 19 © 2007 S. Kenny, Ph. D. , P. Eng. F 4 ENGI 1313 Statics I – Lecture 12 F 2 y

Example 12 -03 (cont. ) n Draw 3 D FBD at Point O Ø Define position and unit vectors for F 2 z F 3 F 1 O 45 40 x 20 © 2007 S. Kenny, Ph. D. , P. Eng. F 4 ENGI 1313 Statics I – Lecture 12 F 2 y

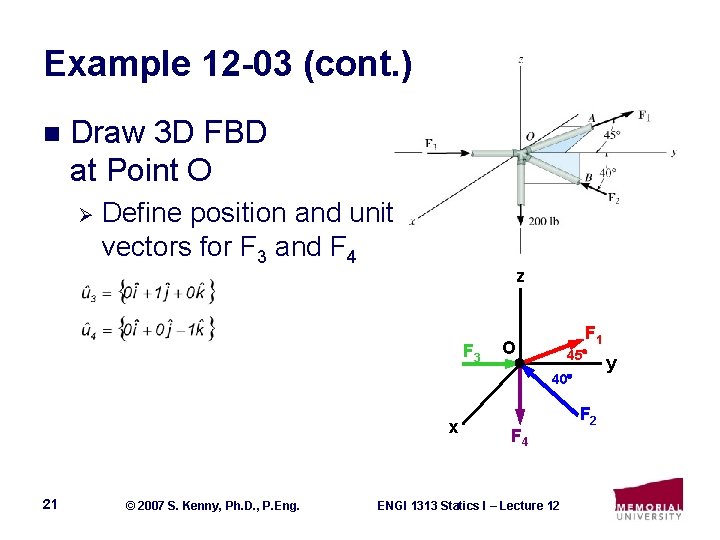
Example 12 -03 (cont. ) n Draw 3 D FBD at Point O Ø Define position and unit vectors for F 3 and F 4 z F 3 F 1 O 45 40 x 21 © 2007 S. Kenny, Ph. D. , P. Eng. F 4 ENGI 1313 Statics I – Lecture 12 F 2 y

Example 12 -03 (cont. ) n Unit and Force Vectors z F 3 F 1 O 45 40 x 22 © 2007 S. Kenny, Ph. D. , P. Eng. F 4 ENGI 1313 Statics I – Lecture 12 F 2 y

Example 12 -03 (cont. ) n Fx Equilibrium z F 3 F 1 O 45 40 x 23 © 2007 S. Kenny, Ph. D. , P. Eng. F 4 ENGI 1313 Statics I – Lecture 12 F 2 y

Example 12 -03 (cont. ) n Fz Equilibrium z F 3 F 1 O 45 40 x 24 © 2007 S. Kenny, Ph. D. , P. Eng. F 4 ENGI 1313 Statics I – Lecture 12 F 2 y

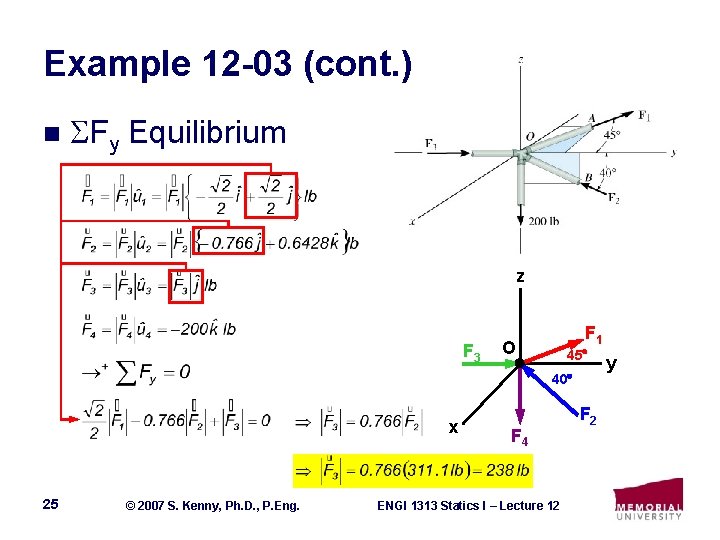
Example 12 -03 (cont. ) n Fy Equilibrium z F 3 F 1 O 45 40 x 25 © 2007 S. Kenny, Ph. D. , P. Eng. F 4 ENGI 1313 Statics I – Lecture 12 F 2 y

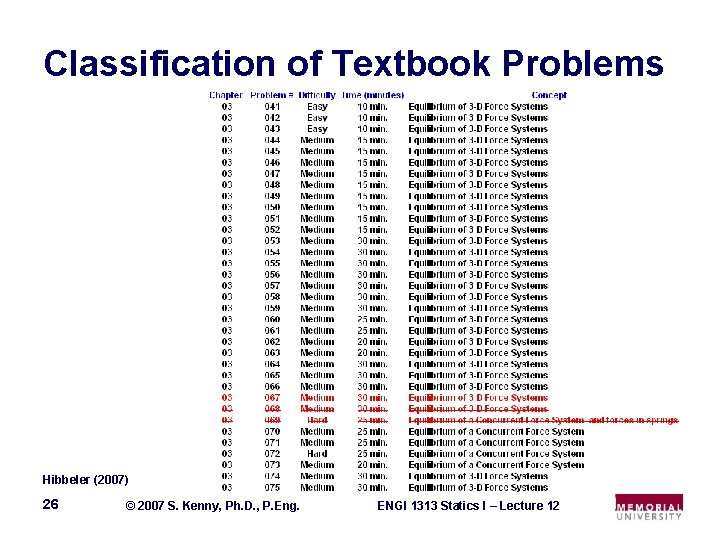
Classification of Textbook Problems Hibbeler (2007) 26 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 12

References http: //en. wikipedia. org n Hibbeler (2007) n http: //wps. prenhall. com/esm_hibbeler_eng mech_1 n 27 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 12