ENGI 1313 Mechanics I Lecture 05 Cartesian Vectors

  • Slides: 33
Download presentation
ENGI 1313 Mechanics I Lecture 05: Cartesian Vectors Shawn Kenny, Ph. D. , P.

ENGI 1313 Mechanics I Lecture 05: Cartesian Vectors Shawn Kenny, Ph. D. , P. Eng. Assistant Professor Faculty of Engineering and Applied Science Memorial University of Newfoundland spkenny@engr. mun. ca

Chapter 2 Objectives to review concepts from linear algebra n to sum forces, determine

Chapter 2 Objectives to review concepts from linear algebra n to sum forces, determine force resultants and resolve force components for 2 D vectors using Parallelogram Law n to express force and position in Cartesian vector form n to introduce the concept of dot product n 2 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 05

Lecture 05 Objectives to further examine Cartesian vector notation and extend to representation of

Lecture 05 Objectives to further examine Cartesian vector notation and extend to representation of a 3 D vector n to sum 3 D concurrent force systems n 3 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 05

Recall 2 D Cartesian Vector n Coplanar Force Vector Summation Ø Unit vector dimensionless

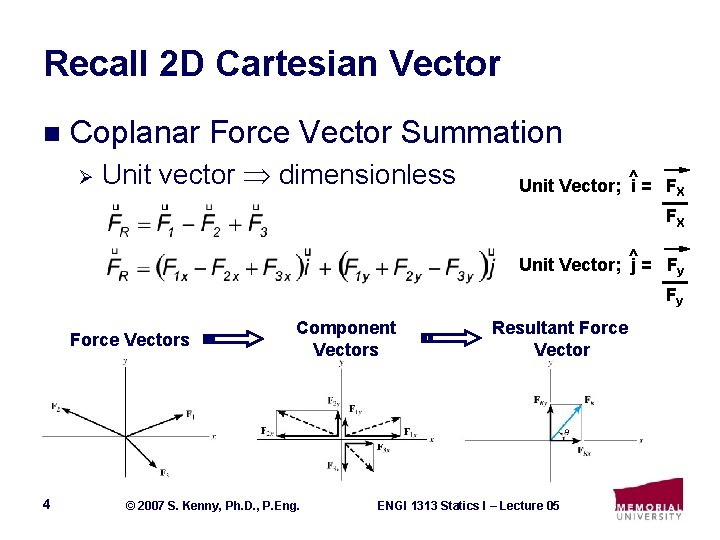
Recall 2 D Cartesian Vector n Coplanar Force Vector Summation Ø Unit vector dimensionless ^ Unit Vector; i = FX FX ^ Unit Vector; j = Fy Fy Force Vectors 4 Component Vectors © 2007 S. Kenny, Ph. D. , P. Eng. Resultant Force Vector ENGI 1313 Statics I – Lecture 05

Extend to 3 D n Why Use Vectors Ø n Rectangular Coordinate System Ø

Extend to 3 D n Why Use Vectors Ø n Rectangular Coordinate System Ø 5 Simplifies mathematical operations Right-hand rule © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 05

Cartesian Vector in 3 D n Three Unit Vectors Ø Component magnitude • Ax,

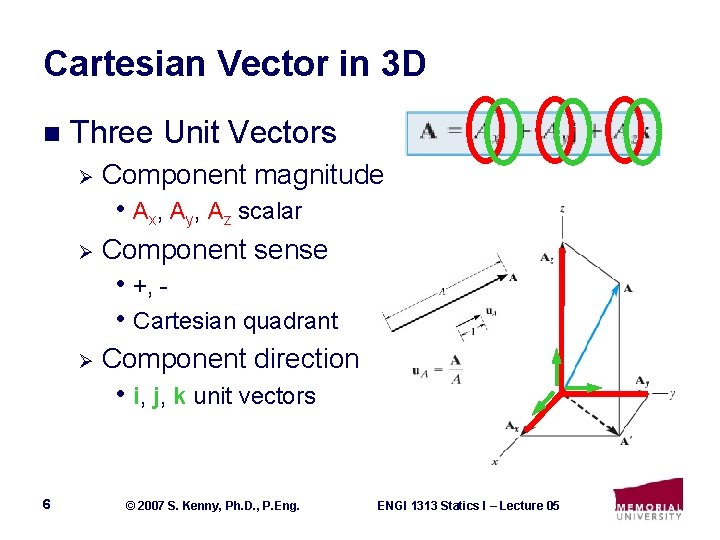
Cartesian Vector in 3 D n Three Unit Vectors Ø Component magnitude • Ax, Ay, Az scalar Ø Component sense • +, • Cartesian quadrant Ø Component direction • i, j, k unit vectors 6 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 05

Summation Cartesian Vectors in 3 D n 7 Use 2 D Principles Ø Vector

Summation Cartesian Vectors in 3 D n 7 Use 2 D Principles Ø Vector A Ø Vector B © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 05

Cartesian Vector Magnitude n Successive Application of 2 D Principle Pythagorean theorem Ø Find

Cartesian Vector Magnitude n Successive Application of 2 D Principle Pythagorean theorem Ø Find components Ax and Ay Ø Ø Combine with z component • Magnitude A of vector A 8 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 05

Cartesian Vector Direction n Coordinate Direction Angle Ø Vector tail with coordinate axis •

Cartesian Vector Direction n Coordinate Direction Angle Ø Vector tail with coordinate axis • , , and • Range from 0 to 180 Ø 9 Visualization aid using right rectangular prism © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 05

Cartesian Vector Direction (cont. ) n Coordinate Direction Angle, Ø 10 Measured +x-axis to

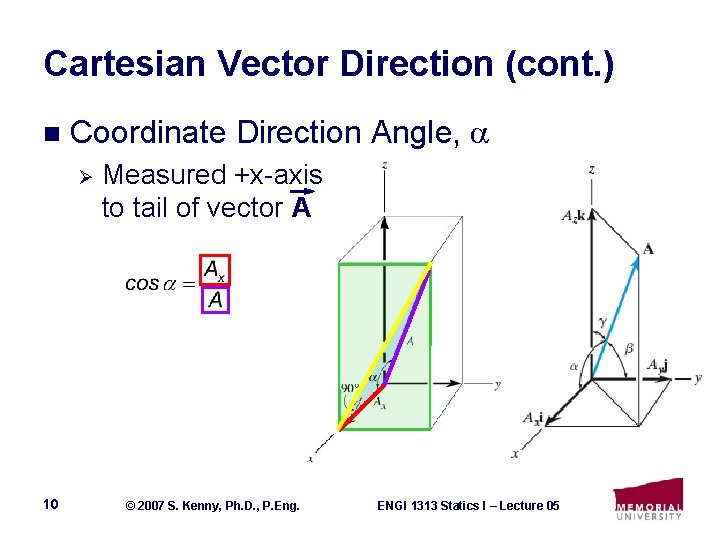
Cartesian Vector Direction (cont. ) n Coordinate Direction Angle, Ø 10 Measured +x-axis to tail of vector A © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 05

Cartesian Vector Direction (cont. ) n Coordinate Direction Angle, Ø 11 Measured +y-axis to

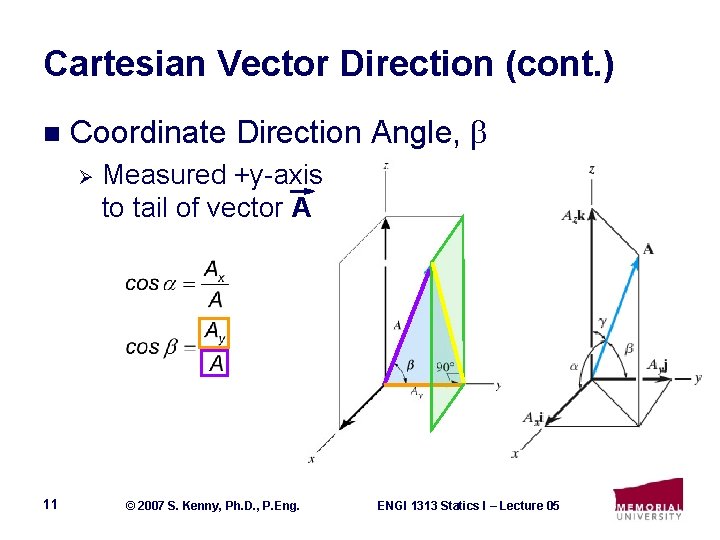
Cartesian Vector Direction (cont. ) n Coordinate Direction Angle, Ø 11 Measured +y-axis to tail of vector A © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 05

Cartesian Vector Direction (cont. ) n Coordinate Direction Angle, Ø 12 Measured +z-axis to

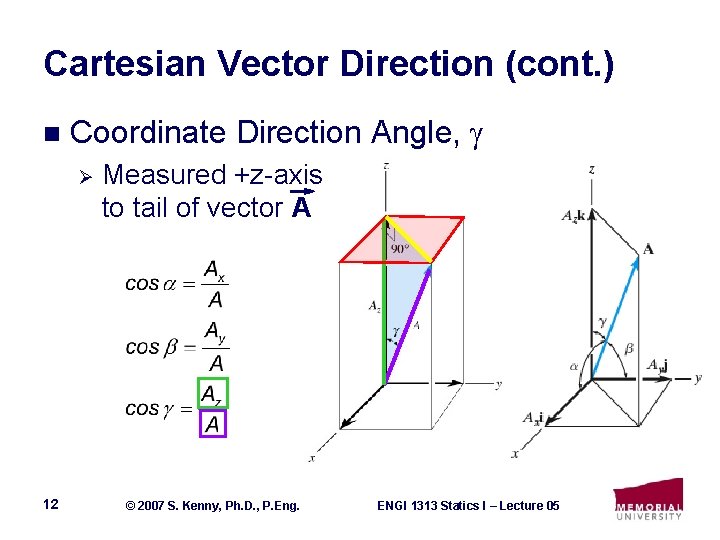
Cartesian Vector Direction (cont. ) n Coordinate Direction Angle, Ø 12 Measured +z-axis to tail of vector A © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 05

Cartesian Vector Direction (cont. ) n Direction Cosines Ø 13 Coordinate direction angles (

Cartesian Vector Direction (cont. ) n Direction Cosines Ø 13 Coordinate direction angles ( , , & ) determined by cos-1 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 05

Cartesian Vector Direction (cont. ) n Express as Cartesian Vector, A n Recall Unit

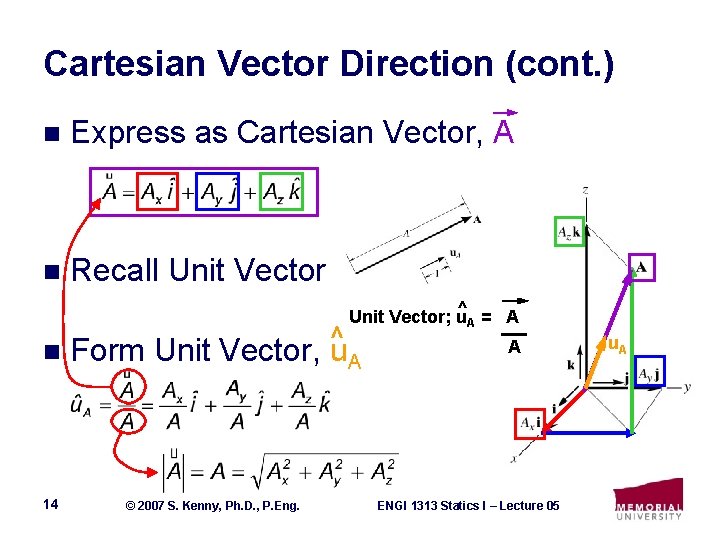
Cartesian Vector Direction (cont. ) n Express as Cartesian Vector, A n Recall Unit Vector ^ = A Unit Vector; u A n Form Unit Vector, ^u. A 14 © 2007 S. Kenny, Ph. D. , P. Eng. A ENGI 1313 Statics I – Lecture 05 u. A

Cartesian Vector Direction (cont. ) n Unit Vector, ^u. A n Relate to Direction

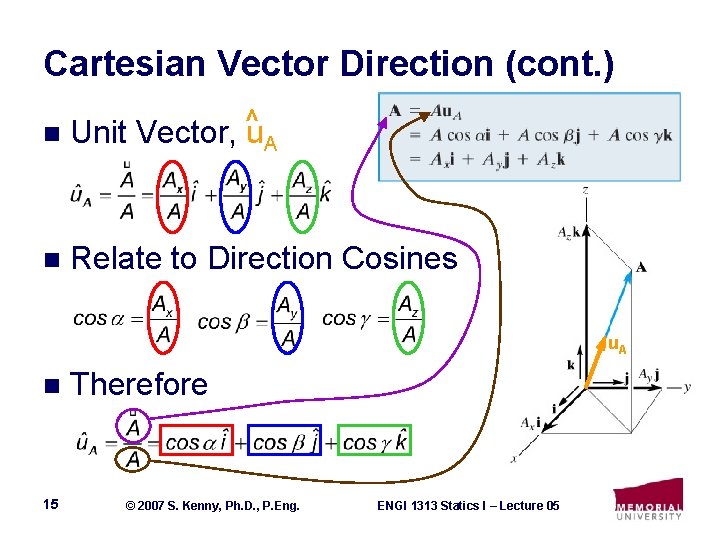
Cartesian Vector Direction (cont. ) n Unit Vector, ^u. A n Relate to Direction Cosines u. A n 15 Therefore © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 05

Cartesian Vector Direction (cont. ) n n 16 ^ | Find Unit Vector Amplitude,

Cartesian Vector Direction (cont. ) n n 16 ^ | Find Unit Vector Amplitude, | u A Ø Recall general case for vector and magnitude Ø Where the unit vector and magnitude is Therefore © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 05

Cartesian Vector Orientation (cont. ) n Typical Cartesian Vector Problems Ø Magnitude and coordinate

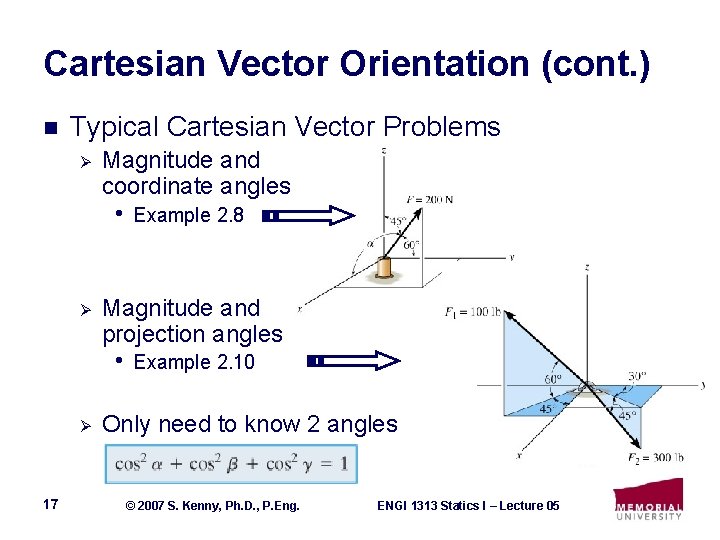
Cartesian Vector Orientation (cont. ) n Typical Cartesian Vector Problems Ø Magnitude and coordinate angles • Ø Magnitude and projection angles • Ø 17 Example 2. 8 Example 2. 10 Only need to know 2 angles © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 05

Comprehension Quiz 5 -01 n If you only know u. A (unit vector) you

Comprehension Quiz 5 -01 n If you only know u. A (unit vector) you can determine the ____ of A uniquely. Ø Ø n Answer Ø 18 A) magnitude (A) B) angles ( , , and ) C) components (Ax, Ay, & Az) D) All of the above B Unit vector (u. A) defines direction |A| defines magnitude © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 05

Example Problem 5 -01 G= 80 lb = 111 = 69. 3 Forces F

Example Problem 5 -01 G= 80 lb = 111 = 69. 3 Forces F and G are applied to a hook. Force F makes 60° angle with the X-Y plane. Force G has a magnitude of 80 lb with = 111° and = 69. 3°. n Find the resultant force in Cartesian vector form n 19 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 05

Example Problem 5 -01 (cont. ) n G= 80 lb = 111 = 69.

Example Problem 5 -01 (cont. ) n G= 80 lb = 111 = 69. 3 Resolve Force F components Fz F Fy n 20 Fx Cartesian Vector Notation © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 05

Example Problem 5 -01 (cont. ) n G= 80 lb = 111 = 69.

Example Problem 5 -01 (cont. ) n G= 80 lb = 111 = 69. 3 Determine for Vector G 21 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 05

Example Problem 5 -01 (cont. ) n Coordinate Direction Angles =111 -x z G

Example Problem 5 -01 (cont. ) n Coordinate Direction Angles =111 -x z G = 80 lb = 111 x 22 y Unit circle © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 05

Example Problem 5 -01 (cont. ) n Coordinate Direction Angles and -x z =

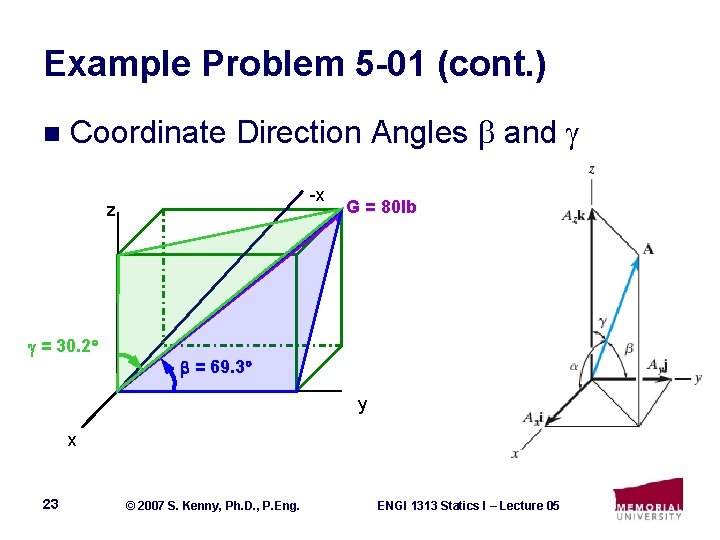
Example Problem 5 -01 (cont. ) n Coordinate Direction Angles and -x z = 30. 2 G = 80 lb = 69. 3 y x 23 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 05

Example Problem 5 -01 (cont. ) n Cartesian Vector G -x z G =

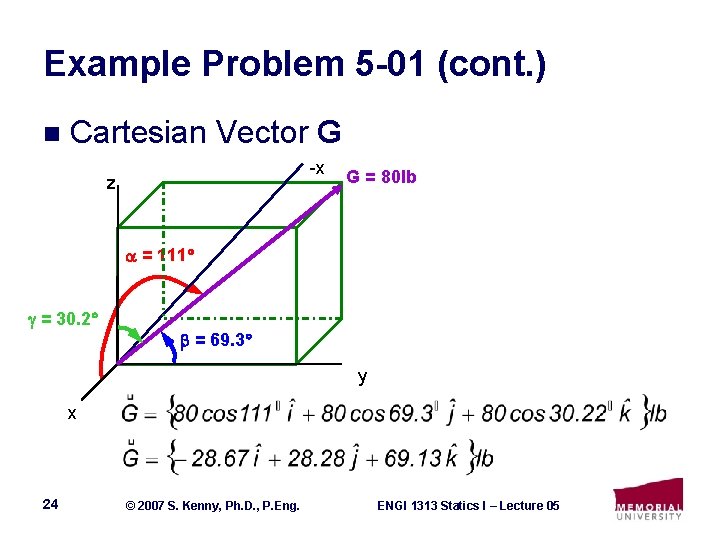
Example Problem 5 -01 (cont. ) n Cartesian Vector G -x z G = 80 lb = 111 = 30. 2 = 69. 3 y x 24 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 05

Example Problem 5 -01 (cont. ) n Combine Force Vectors n Resultant Vector 25

Example Problem 5 -01 (cont. ) n Combine Force Vectors n Resultant Vector 25 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 05 G= 80 lb = 111 = 69. 3

Group Problem 5 -01 n Problem 2 -57 (Hibbeler, 2007) Ø 26 Determine the

Group Problem 5 -01 n Problem 2 -57 (Hibbeler, 2007) Ø 26 Determine the magnitude and coordinate direction angles of F 1 and F 2. Sketch each force on an x, y, z reference. © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 05

Group Problem 5 -01 (cont. ) n 27 Force F 1 © 2007 S.

Group Problem 5 -01 (cont. ) n 27 Force F 1 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 05

Group Problem 5 -01 (cont. ) n 28 Force F 2 © 2007 S.

Group Problem 5 -01 (cont. ) n 28 Force F 2 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 05

Group Problem 5 -02 n Problem 2 -59 (Hibbeler, 2007) Ø 29 Determine the

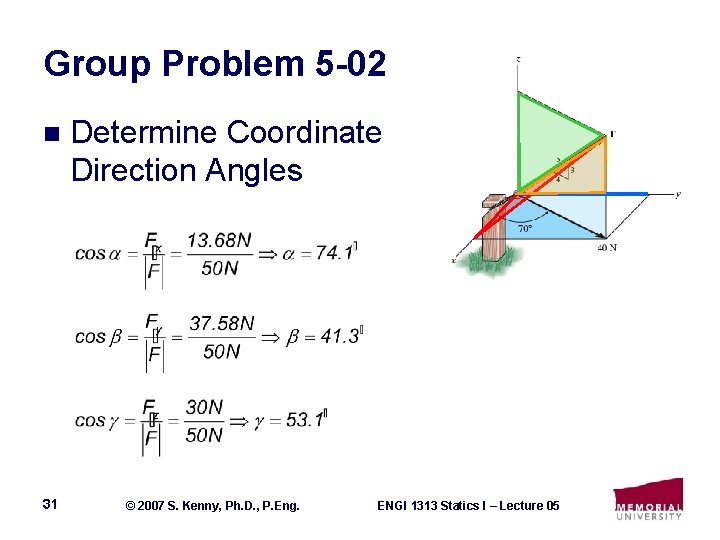
Group Problem 5 -02 n Problem 2 -59 (Hibbeler, 2007) Ø 29 Determine the magnitude and coordinate angles of F acting on the stake. © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 05

Group Problem 5 -02 n Determine F and components F Fx Fy 30 ©

Group Problem 5 -02 n Determine F and components F Fx Fy 30 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 05 Fz

Group Problem 5 -02 n 31 Determine Coordinate Direction Angles © 2007 S. Kenny,

Group Problem 5 -02 n 31 Determine Coordinate Direction Angles © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 05

Classification of Textbook Problems n Hibbeler (2007) Problem Set 2 -57 32 Degree of

Classification of Textbook Problems n Hibbeler (2007) Problem Set 2 -57 32 Degree of Estimated Difficulty Time Concept Cartesian: Magnitude & direction Medium 10 -15 min 2 -58 to 2 -60 Cartesian: Forces Easy 5 -10 min 2 -61 to 2 -69 Cartesian; Force components & resultant Easy 5 -10 min 2 -70 to 2 -71 Cartesian; Force components & resultant Hard 20 -25 min 2 -72 to 2 -78 Cartesian; Force components & resultant Medium 15 -20 min © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 05

References Hibbeler (2007) n http: //wps. prenhall. com/esm_hibbeler_eng mech_1 n en. wikipedia. org n

References Hibbeler (2007) n http: //wps. prenhall. com/esm_hibbeler_eng mech_1 n en. wikipedia. org n 33 © 2007 S. Kenny, Ph. D. , P. Eng. ENGI 1313 Statics I – Lecture 05