ENGG 2013 Unit 9 3 x 3 Determinant

ENGG 2013 Unit 9 3 x 3 Determinant Feb, 2011.

Last time • 2 2 determinant • Compute the area of a parallelogram by determinant • A formula for 2 x 2 matrix inverse kshum ENGG 2013 2

Today • 3 3 determinant and its properties • Using determinant, we can – test whether three vectors lie on the same plane – solve 3 3 linear system – test whether the inverse of a 3 3 matrix exists kshum ENGG 2013 3

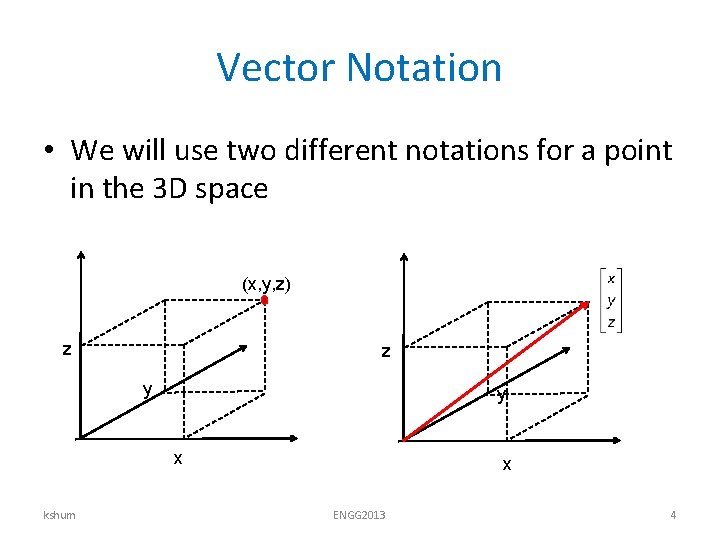
Vector Notation • We will use two different notations for a point in the 3 D space (x, y, z) z z y y x kshum x ENGG 2013 4

2 2 determinant Notation for 2 2 determinant : + – How to calculate: ad – bc - bc kshum ENGG 2013 ad 5

3 3 determinant Notation for 3 3 determinant : Definition: kshum ENGG 2013 6

Rule of Sarrus + + + – – – Pierre Frédéric Sarrus (1798 – 1861) kshum ENGG 2013 7

Volume of parallelepiped • Geometric meaning – The magnitude of 3 3 determinant is the volume of a parallelepiped z y x kshum ENGG 2013 8

Co-planar zero determinant • Determinant = 0 Volume = 0 the three vectors lie on the same plane z y A collection of vectors are said to be co-planar if they lie on the same plane. x kshum ENGG 2013 9

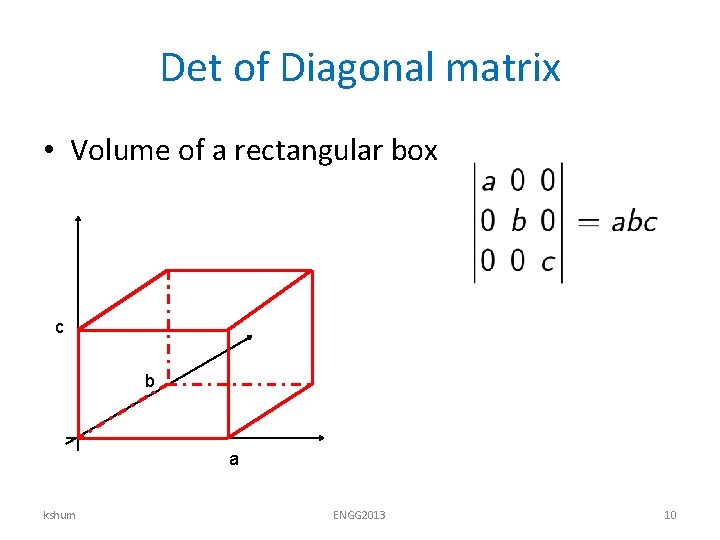
Det of Diagonal matrix • Volume of a rectangular box c b a kshum ENGG 2013 10

Transpose has the same determinant + + + – – – Compare with kshum ENGG 2013 11

Volume of parallelepiped • In computing the volume of a parallelepiped, it does not matter whether we write the vector horizontally or vertically in the determinant z Volume of parallelepiped with vertices (0, 0, 0), (1, 2, 0), (2, 0, 1), (– 1, 1, 3) equals to the absolute value of y or x kshum ENGG 2013 12

Question • Do (1, 1, 1), (2, 3, 4), (5, 6, 7) and (8, 9, 10) lie on the same plane? kshum ENGG 2013 13

Cramer’s rule • If the determinant of a 3 3 matrix A is non-zero, we can solve the linear system A x = b by Cramer’s rule. • The solution to or equivalently A is x b Gabriel Cramer (1704 -1752) kshum ENGG 2013 14

PROPERTIES OF DETERMINANT kshum ENGG 2013 15

How to show that Cramer’s rule does give the correct answer? • The Cramer’s rule is a theorem, which requires a proof, or verification. • We need some properties of determinant. kshum ENGG 2013 16

Properties of determinant 1. Taking transpose does not change the value of determinant We have already verified this property in p. 11 kshum ENGG 2013 17

Meta-property • Because 1. After taking the transpose of a matrix, columns become rows, and rows become column. 2. Taking the transpose of a matrix does not change the value of its determinant. • Therefore, any row property of determinant is automatically a column property, and vice versa. kshum ENGG 2013 18

Properties of determinant 2. If any row or column is zero, then the determinant is 0. For example kshum ENGG 2013 19

Properties of determinant 3. If any two columns (or rows) are the identical, then the determinant is zero. For example, if the second column and the third column are the same, then kshum ENGG 2013 20

Properties of Determinant 4. If we exchange of the two columns (or two rows), the determinant is multiplied by – 1. For example, if we exchange the column 2 and column 3, we have The first kind of elementary row operation kshum ENGG 2013 21

Multiply by a constant 5. If we multiply a row (or a column) by a constant k, the value of determinant increases by a factor of k. The 2 nd kind of elementary row operation For example, if we multiply the third row by a constant k, kshum ENGG 2013 22

An additive property 6. If a row (or column) of a determinant is the sum of two rows (or columns), the determinant can be split as the sum of two determinants For example, if the first column is the sum of two column vectors, then we have kshum ENGG 2013 23

Properties of Determinant 7. If we add a constant multiple of a row (column) to the other row (column), the determinant does not change. The 3 rd kind of elementary row operation For example, if we replace the 3 rd column by the sum of the 3 rd column and k times the 2 nd column, kshum ENGG 2013 24

Summary on the effect of the elementary row (or column) operations on determinant • Exchange two rows (or columns) change the sign of determinant • Multiply a row (or a column) by a constant k multiply the determinant by k • Add a constant multiple of a row (column) to another row (or column) no change kshum ENGG 2013 25

Proof of the Cramer’s rule • The solution to is Verification for x 1: Substitute the value of b 1, b 2 and b 3 in the first column of A. Verification for x 2: Substitute the value of b 1, b 2 and b 3 in the second column of A. Cramer’s rule in wikipedia Etc. kshum ENGG 2013 26

Because x 1, x 2, x 3 satisfy the system of linear equations, we have By substitution Property 6 Property 5 =0 kshum ENGG 2013 =0 By Property 3 27

MINOR AND COFACTOR kshum ENGG 2013 28

Another way to compute det Group the six terms as 3 3 determinant can be computed in terms of 2 2 determinant kshum ENGG 2013 29

Minor and cofactor • A minor of a matrix is the determinant of some smaller square matrix, obtained by removing one or more of its rows and columns. • Notation: Given a matrix A, the minor obtained by removing the i-th row and j-th column is denoted by Aij. It is also called the minor of the (i, j)-entry aij in A. kshum ENGG 2013 30

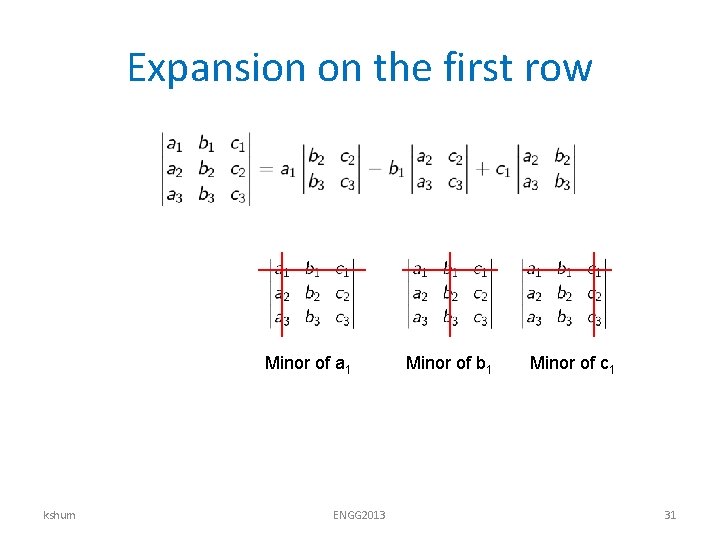
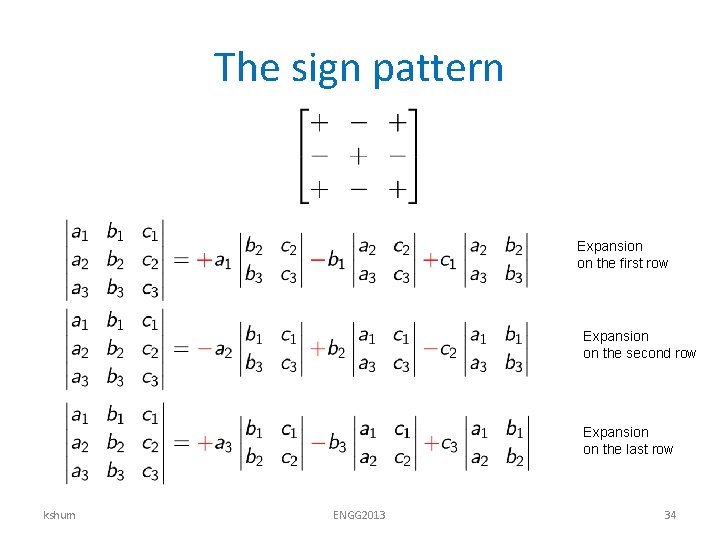
Expansion on the first row Minor of a 1 kshum ENGG 2013 Minor of b 1 Minor of c 1 31

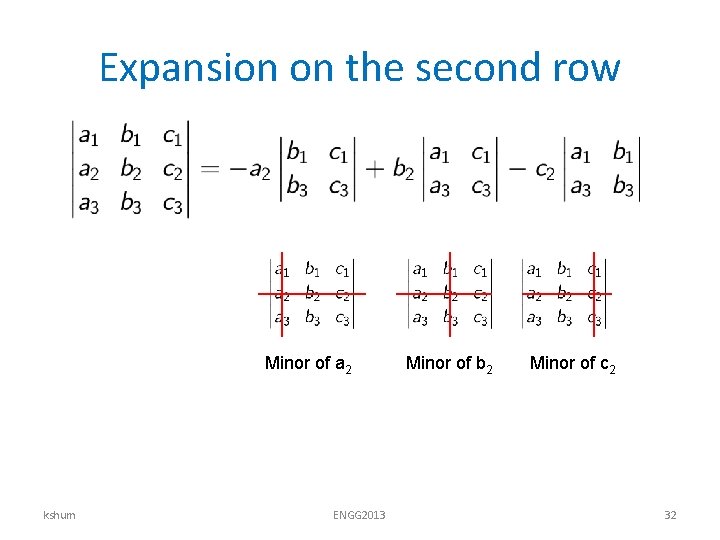
Expansion on the second row Minor of a 2 kshum ENGG 2013 Minor of b 2 Minor of c 2 32

Expansion on the third row Minor of a 3 kshum ENGG 2013 Minor of b 3 Minor of c 3 33

The sign pattern Expansion on the first row Expansion on the second row Expansion on the last row kshum ENGG 2013 34

Column expansion We have similar recursive formula for determinant by column expansion For example, Computation on the third column is easy, because there are lots of zeros. kshum ENGG 2013 35

Cofactor • The minor together with the appropriate sign is called cofactor. • For The sign The cofactor of Cij is defined as Expansion on the i-th row (i=1, 2, 3): The minor of aij Expansion on the j-th column (j=1, 2, 3): kshum ENGG 2013 36

A formula for matrix inverse Suppose that det A is nonzero. (Beware of the subscripts) Usually called the adjoint of A Three steps in computing above formula 1. for i, j = 1, 2, 3, replace each aij by cofactor Cij 2. Take the transpose of the resulting matrix. 3. divide by the determinant of A. kshum ENGG 2013 37

A Quotation Algebra is but written geometry; geometry is but drawn algebra. --- Sophie Germain (1776 -1831) L'algèbre n'est qu'une géométrie écrite; la géométrie n'est qu'une algèbre figurée kshum ENGG 2013 38