ENG 2410 Digital Design Week 5 Design of

ENG 2410 Digital Design: Week #5 “Design of Arithmetic Circuits: Part 2” S. Areibi School of Engineering University of Guelph

Topics ¡ Design of Binary Ripple Carry Adder l l Design of Half Adders Design of Full Adders Design of BCD Adders ¡ 1’s and 2’s Complement ¡ Design of Binary Subtractor ¡ Design of Binary Adder-Subtractors ¡ Design of Binary Multipliers ¡

Resources Chapter #5, Mano Sections l l l 5. 2 5. 3 5. 4 5. 5 5. 7 Binary Adders Binary Subtraction Binary Adders-Subtractors Binary Multiplications HDL Representations -- VHDL

Signed Numbers

Negative Numbers « Computers Represent Information in ‘ 0’s and ‘ 1’s ● ‘+’ and ‘−’ signs have to be represented in ‘ 0’s and ‘ 1’s « 3 Systems ● Signed Magnitude ● 1’s Complement ● 2’s Complement All three use the left-most bit to represent the sign: ♦ ‘ 0’ positive ♦ ‘ 1’ negative 5

Signed Binary Numbers First review signed representations 1. Signed magnitude l l 2. 3. Left bit is sign, 0 positive, 1 negative Other bits are magnitude of the number 0 0001001 +9 1 0001001 -9 1’s Complement 2’s Complement 6

Signed Magnitude Representation « Magnitude is magnitude, does not change with sign S Magnitude (Binary) (+3)10 ( 0 0 1 1 )2 (− 3)10 ( 1 0 1 1 )2 Sign Magnitude 7

1’s Complement Representation « Positive numbers are represented in “Binary” 0 Magnitude (Binary) « Negative numbers are represented in “ 1’s Comp. ” 1 Code (1’s Comp. ) (+3)10 (0 011)2 (− 3)10 (1 100)2 100 is the 1’s complement of 011 « There are 2 representations for ‘ 0’!!!!!! (+0)10 (0 000)2 (− 0)10 (1 111)2 8

1’s Complement Range Decimal 1’s Comp. « 4 -Bit Representation 4 2 = 16 Combinations − 7 ≤ Number ≤ + 7 3 3 − 2 -1 ≤ Number ≤ +2 − 1 « n-Bit Representation − 2 n− 1 -1 ≤ Number ≤ +2 n− 1 +7 +6 +5 +4 +3 +2 +1 +0 − 1 − 2 − 3 − 4 − 5 − 6 − 7 0111 0110 0101 0100 0011 0010 0001 0000 1111 1110 1101 1100 1011 1010 1001 1000 9

2’s Complement Representation « Positive numbers are represented in “Binary” 0 Magnitude (Binary) « Negative numbers are represented in “ 2’s Comp. ” 1 Code (2’s Comp. ) (+3)10 (0 011)2 (− 3)10 (1 101)2 101 is the 2’s complement of 011 « There is 1 representation for ‘ 0’ 1’s Comp. 1111 (+0)10 (0 000)2 + 1 (− 0)10 (0 000)2 1 0000 10

2’s Complement Range Decimal 2’s Comp. « 4 -Bit Representation 4 2 = 16 Combinations − 8 ≤ Number ≤ + 7 3 3 − 2 ≤ Number ≤ + 2 − 1 « n-Bit Representation − 2 n− 1 ≤ Number ≤ + 2 n− 1 +7 +6 +5 +4 +3 +2 +1 +0 − 1 − 2 − 3 − 4 − 5 − 6 − 7 − 8 0111 0110 0101 0100 0011 0010 0001 0000 1111 1110 1101 1100 1011 1010 1001 1000 11

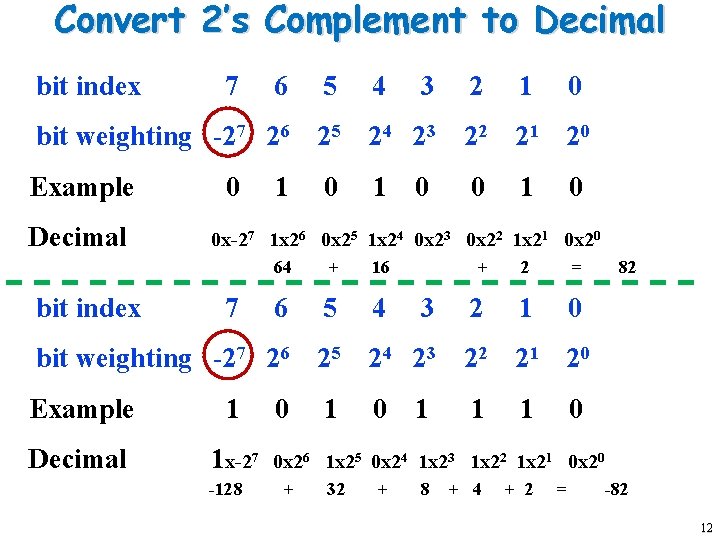
Convert 2’s Complement to Decimal bit index 7 6 5 4 3 2 1 0 bit weighting -27 26 25 24 23 22 21 20 Example Decimal bit index 0 1 0 0 x-27 1 x 26 0 x 25 1 x 24 0 x 23 0 x 22 1 x 21 0 x 20 7 64 + 16 6 5 4 3 + 2 = 2 1 0 82 bit weighting -27 26 25 24 23 22 21 20 Example 1 Decimal 1 x-27 -128 0 1 1 1 0 0 x 26 1 x 25 0 x 24 1 x 23 1 x 22 1 x 21 0 x 20 + 32 + 8 + 4 + 2 = -82 12

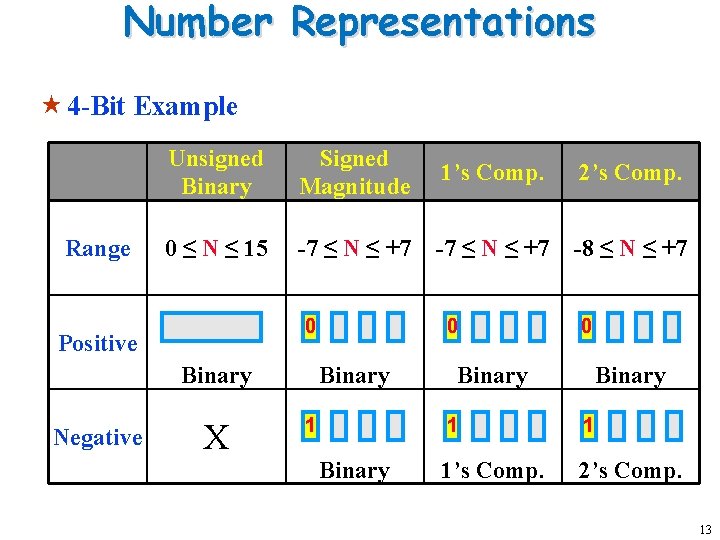
Number Representations « 4 -Bit Example Range Unsigned Binary Signed Magnitude 1’s Comp. 2’s Comp. 0 ≤ N ≤ 15 -7 ≤ N ≤ +7 -8 ≤ N ≤ +7 0 Positive Binary Negative X 0 Binary 1 Binary 0 Binary 1 1 1’s Comp. 2’s Comp. 13

Example in 8 -bit byte ¡ Represent +9 in different ways Signed magnitude 1’s Complement 2’s Complement ¡ 00001001 The Same! Represent -9 in different ways Signed magnitude 1’s Complement 2’s Complement 10001001 11110110 11110111 Same in sign Different in magnitude 14

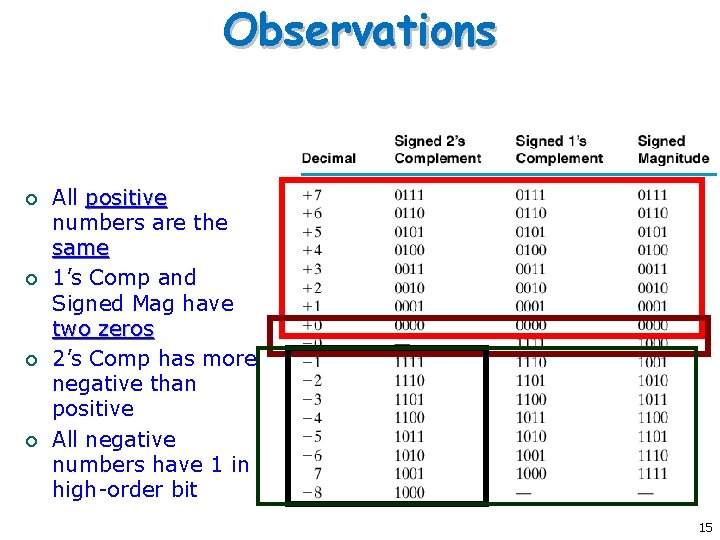
Observations ¡ ¡ All positive numbers are the same 1’s Comp and Signed Mag have two zeros 2’s Comp has more negative than positive All negative numbers have 1 in high-order bit 15

Advantages/Disadvantages Signed magnitude has problem that we need to correct after subtraction L One’s complement has a positive and negative zero J Two’s complement is most popular L l l i. e. , arithmetic operations are easy No correction is required. 16

Signed Magnitude “Arithmetic” « Magnitude is magnitude, does not change with sign S Magnitude (Binary) (+3)10 ( 0 0 1 1 )2 (− 3)10 ( 1 0 1 1 )2 Sign Magnitude « Can’t include the sign bit in ‘Addition’ 0 0 1 1 (+3)10 + 1 0 1 1 (− 3)10 1 1 1 0 (− 6)10 17

Signed Magnitude Representation ¡ The signed-magnitude system is used in ordinary arithmetic, but is awkward when employed in computer arithmetic (Why? ) Why? 1. 2. ¡ We have to separately handle the sign Perform the correction if necessary!! Therefore the signed complement (1’s complement and 2’s complement number representations) is normally used 18

Signed Magnitude Arithmetic Complex Rules!! The addition of two numbers M+N in the sign magnitude system follows the rules of ordinary arithmetic: ¡ ¡ If the signs are the same, same we add the two magnitudes and give the sum the sign of M. If the signs are different, different we subtract the magnitude of N from the magnitude of M. The absence or presence of an end borrow then determines: l l l ¡ ¡ The sign of the result. Whether or not a correction is performed. Example: (0 0011001) + (1 0100101) l ¡ ¡ 0011001 – 0100101 = 1110100 End borrow of 1 occurs, M < N!! Sign of result should be that of N, Also correct result by taking the 2’s complement of result 19

Binary Subtraction Using 1’s Comp. Addition « Change “Subtraction” to “Addition” « If “Carry” = 1 then add it to the LSB, and the result is positive (in Binary) « If “Carry” = 0 then the result is negative (in 1’s Comp. ) (5)10 – (1)10 (5)10 – (6)10 (+5)10 + (-1)10 (+5)10 + (-6)10 0101 + 1110 0101 + 1001 1 0011 + 0 1110 0100 1110 +4 − 1 20

2’s Complement ¡ To Add: l ¡ Easy on any combination of positive and negative numbers To subtract: l l Also easy! easy Take 2’s complement of subtrahend Add This performs A + ( -B), same as A – B 21

Binary Subtraction Using 2’s Comp. Addition « Change “Subtraction” to “Addition” « If “Carry” = 1 ignore it, and the result is positive (in Binary) « If “Carry” = 0 then the result is negative (in 2’s Comp. ) (5)10 – (1)10 (5)10 – (6)10 (+5)10 + (-1)10 (+5)10 + (-6)10 0101 + 1111 0101 + 1010 1 0100 0 1111 +4 − 1 22

2’s Comp Addition/Subtraction The numbers below should be in 2’s comp representation ¡ Addition l l ¡ (+6) (-6) + + 13 13 (- 13) (-13) Subtraction l l (-6) - (-13) (+6) - (-13) 23

Addition of Two Positive Numbers ¡ Addition (+6) + 13 = +19 00000110 +6 +00001101 +13 -------00010011 +19 l ¡ If a carry out appears it should be discarded. 24

Addition of : a Positive and Negative Numbers ¡ Addition (-6) + 13 = +7 11111010 (this is 2’s comp of +6) +00001101 -------1 00000111 +7 l ¡ The carry out is discarded 25

Subtraction of Two Numbers The subtraction of two signed binary numbers (when negative numbers are in 2’s complement form) can be accomplished as follows: 1. 2. 3. Take the 2’s complement of the subtrahend (including the sign bit) Add it to the minuend. A Carry out of the sign bit position is discarded. 26

Subtraction of Two Numbers ¡ Subtraction (+6) – (+13) = -7 00000110 - 00001101 + 11110011 (2’s comp) ------------11111001 l ¡ What is 11111001? Take its 2’s complement=> The magnitude is 7 So it must be -7 00000111 27

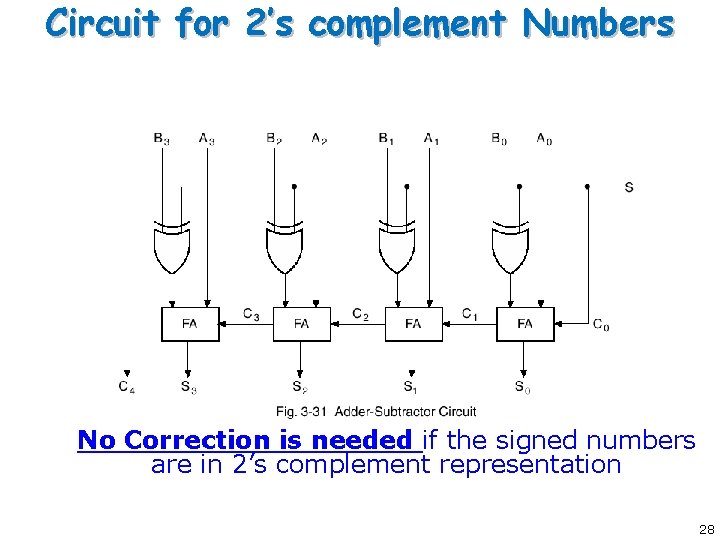
Circuit for 2’s complement Numbers No Correction is needed if the signed numbers are in 2’s complement representation 28

Sign Extension

Sign Extension ¡ ¡ ¡ Sign extension is the operation, in computer arithmetic, of increasing the number of bits of a binary number while preserving the number’s sign (positive/negative) and value. This is done by appending digits to the most significant side of the number Examples: 2’s complement (6 -bits 8 -bits) l 00 1010 0000 1010 2’s complement (5 -bits 8 -bits): l 10001 1111 0001 30

Overflow

Overflow In order to obtain a correct answer when adding and subtracting, we must ensure that the result has a sufficient number of bits to accommodate the sum. ¡ If we start with two n-bit numbers and we end up with a number that is n+1 bits, we say an overflow has occurred. ¡ 1 6 -bit Register 0 1 1 6 -bit Register 1 1 0 0 6 -bit Register 0 1 0 No Overflow 32

Overflow ¡ Two cases of overflow for addition of signed numbers l Two large positive numbers overflow into sign bit ¡ l Two large negative numbers added ¡ ¡ Not enough room for result Same – not enough bits Carry out can be OK 33

Examples ¡ ¡ ¡ Two signed numbers +70 and +80 are stored in 8 bit registers The range of binary numbers, expressed in decimal, that each register can accommodate is from +127 to -128. Since the sum of the two stored numbers is 150, it exceeds the capacity of an 8 -bit register. The same applies for -70 and -80. Adding -70 + (-80) = -150 34

Overflow Detection Carries: 0 1 Carries: 1 0 +70 0 1000110 -70 1 0111010 +80 0 1010000 -80 1 0110000 ----------------+150 1 0010110 -150 0 1101010 1. The addition of +70 and +80 resulted in a negative number! 2. The addition of -70 and -80 also resulted in an incorrect value which is positive number! 3. An overflow condition can be detected by observing the carry into the sign bit position and the carry out of the sign bit position. 4. If the carry in and carry out of the sign bit are not equal an overflow has occurred. 35

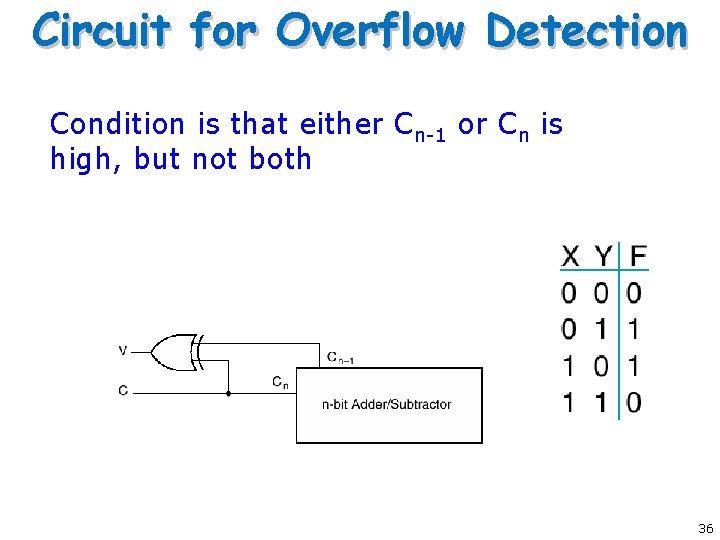
Circuit for Overflow Detection Condition is that either Cn-1 or Cn is high, but not both 36

Binary Multiplication

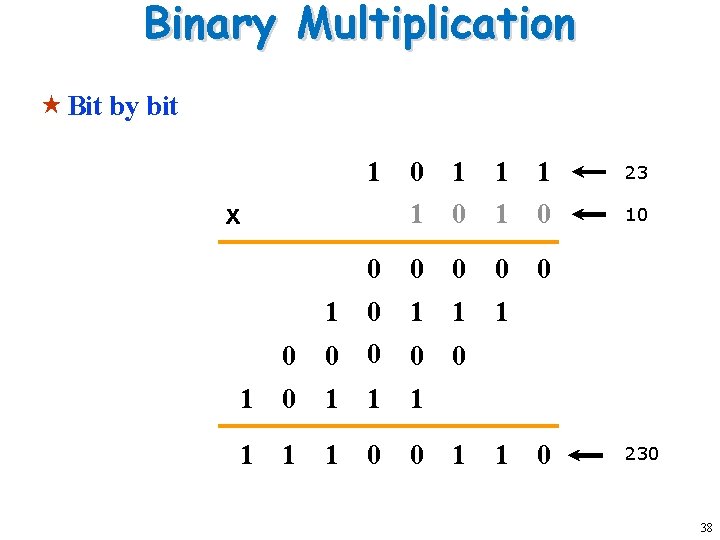
Binary Multiplication « Bit by bit 1 0 1 1 1 23 1 0 10 0 0 1 0 1 1 1 0 0 0 1 1 1 1 0 0 x 1 1 0 230 38

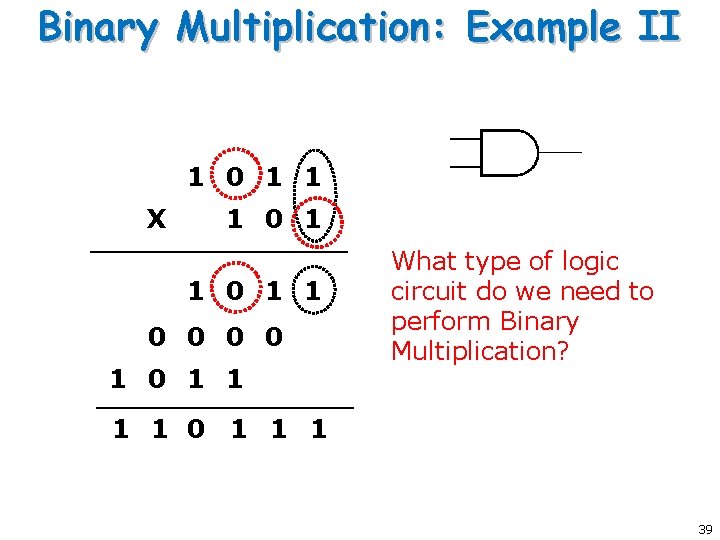
Binary Multiplication: Example II 1 0 1 1 X 1 0 1 1 0 0 1 0 1 1 0 What type of logic circuit do we need to perform Binary Multiplication? 1 1 1 39

Multiplier ¡ ¡ Multiply by doing single-bit multiplies and shifts Combinational circuit to accomplish this? The value of A 0 B 0 Will either be 0 or 1 What type of gate can we use? 40

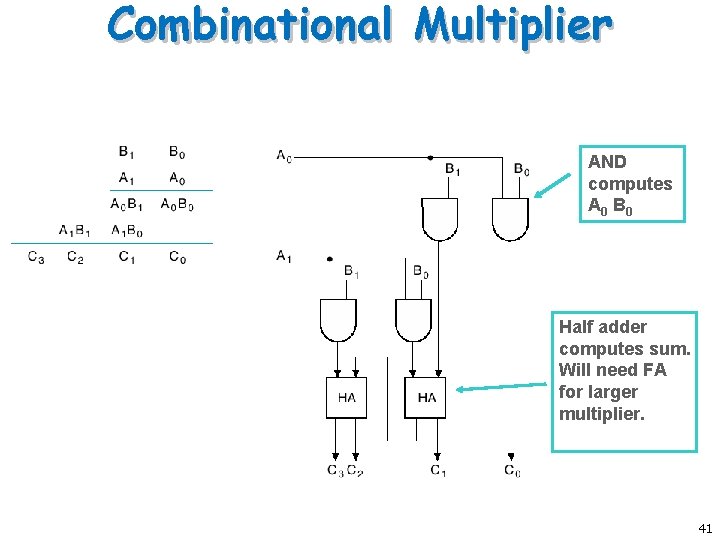
Combinational Multiplier AND computes A 0 B 0 Half adder computes sum. Will need FA for larger multiplier. 41

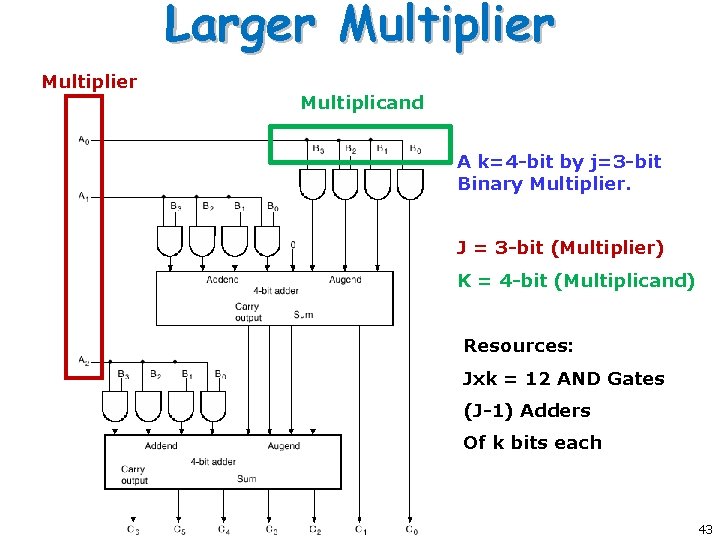
Larger Multiplier: Resources For J multiplier bits and K multiplicand bits we need o o J x K AND gates (J-1) K-bit adders to produce a product of J+K bits. 42

Larger Multiplier Multiplicand A k=4 -bit by j=3 -bit Binary Multiplier. J = 3 -bit (Multiplier) K = 4 -bit (Multiplicand) Resources: Jxk = 12 AND Gates (J-1) Adders Of k bits each 43