ENERGY Work and Power Simple Machines Kinetic Energy




















































































































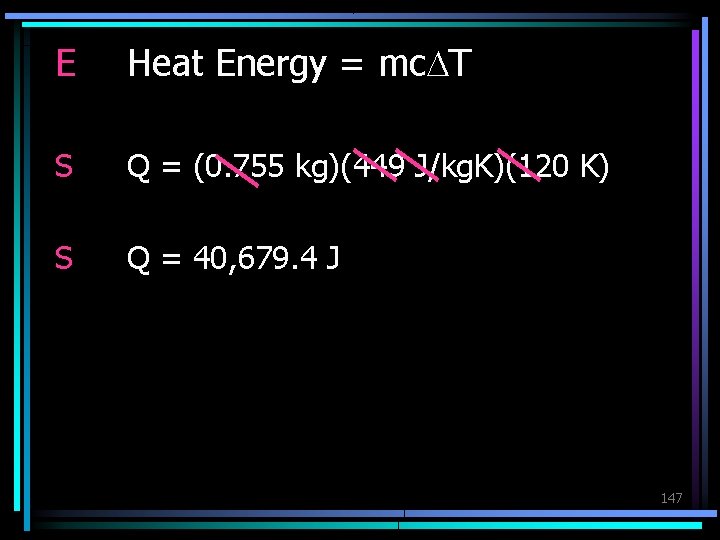





- Slides: 152

ENERGY Work and Power Simple Machines Kinetic Energy Potential Energy

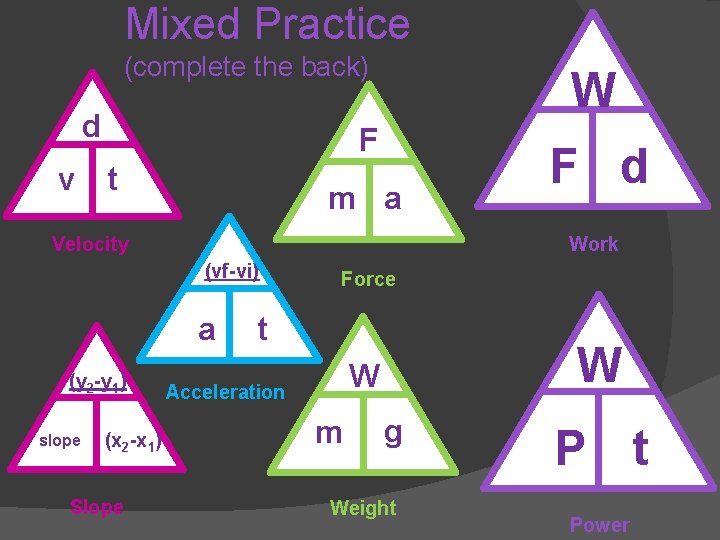
Equations used so far. . . d v F t m a (vf-vi) a t (y 2 -y 1) slope (x 2 -x 1) W m g

WORK AND POWER

Work Occurs when a force causes something to move a distance Motion must be in the same direction as the force

Is this an example of work? force distance yes

Is this work? force distance Yes…if he LIFTS the barbell

Is this work? distance? force No…why not?

Is this work? force distance No…why not?

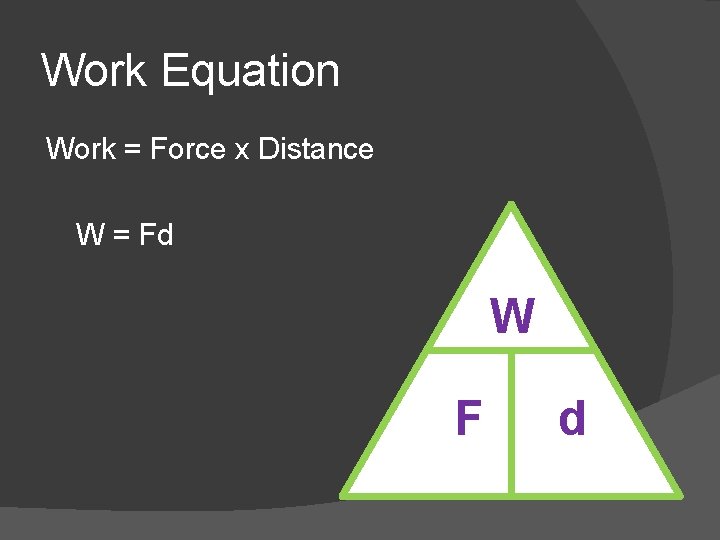
Work Equation Work = Force x Distance W = Fd W F d

Units for Work W = Fd Nm Or Joules (J)

Practice Problem John uses 45 Newtons of force to push his lazy dog 3. 2 meters across the kitchen floor. How much work does John do? F = 45 N d = 3. 2 m W = ? W = Fd W = (45 N)(3. 2 m) W = 144 J s. f. : 140 J

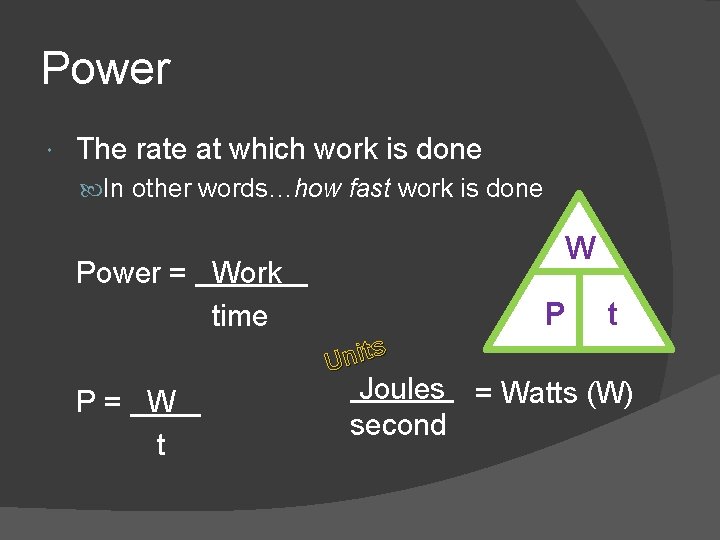
Power The rate at which work is done In other words…how fast work is done Power = Work time W P s Unit P = W t t Joules = Watts (W) second

Practice Problem If John takes 5. 0 seconds to push his dog, what is his power output? W = 144 J t = 5. 0 s P = ? P = W/t P = 144 J/5. 0 s P = 28. 8 W s. f. : 29 W

A crane uses an average force of 5200 N to lift a girder 25 m. How much work does the crane do?

An apple weighing 1 N falls a distance of 1 m. How much work is done on the apple by the force of gravity?

A bicycle's brakes apply 125 N of friction force to the wheels as the bike moves 14. 0 m. How much work do the brakes do?

A mechanic uses a hydraulic lift to raise a 1200 kg car 0. 50 m off the ground. How much work does the lift do on the car?

While rowing across the lake during a race, John does 3960 J of work on the oars in 60. 0 s. What is his power output in watts?

Anna walks up the stairs on her way to class. She weighs 565 N, and the stairs go up 3. 25 m vertically. A. What is her power output if she climbs the stairs in 12. 6 s? B. What is her power output if she climbs the stairs in 10. 5 s?

Assignment: Practice Problems: p. 432 #1 -4 1. 130000 J 2. 1 J 3. 1750 J 4. 5900 J p. 434 # 1 -2 1. 66 W 2 a. 146 W 2 b. 175 W W F d W P t

Review What does the term “work” mean in your everyday life? What does the term “work” mean in Physical Science? Work is the ability to produce a force that causes movement.

Work and Power Practice Problems: Mixed Equations (Front only) W = 237825 J 2. d = 0. 6 m 3. F = 27 N 4. a) P = 494 watts 4. b) d = 3 m 6. W = 300 000 J 1.

Mixed Practice (complete the back) d W F v t m a Velocity Work (vf-vi) a (y 2 -y 1) slope (x 2 -x 1) Slope F d Force t W W Acceleration m g Weight P t Power

Review What does the term “power” mean in Physical Science? Power is the rate (how fast) an individual is able to do work. What are the two main families of simple machines? 1. Lever Family 2. Inclined Plane Family

HOUSEHOLD TOOLS MINI -LAB

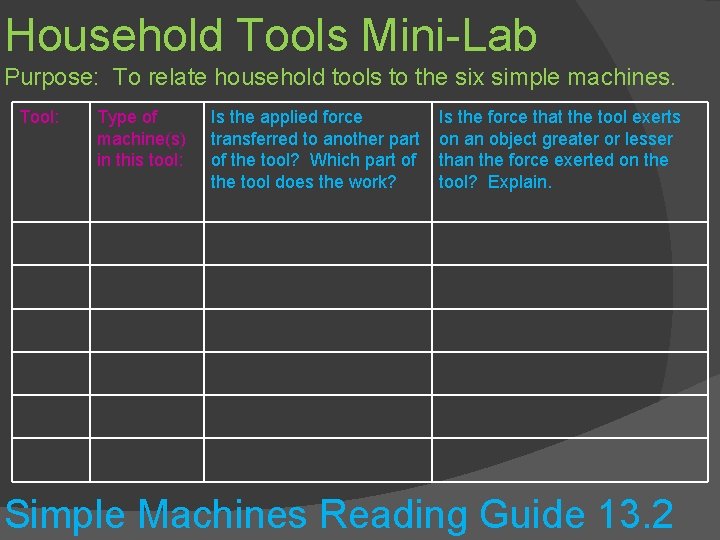
Household Tools Mini-Lab Purpose: To relate household tools to the six simple machines. Tool: Type of machine(s) in this tool: Is the applied force transferred to another part of the tool? Which part of the tool does the work? Is the force that the tool exerts on an object greater or lesser than the force exerted on the tool? Explain. Simple Machines Reading Guide 13. 2

THE 6 SIMPLE MACHINES

Lever Family Inclined Plane Family THE 6 SIMPLE MACHINES

The Lever Family Lever Pulley Wheel & Axle

Lever Family 1. LEVER

*Levers-First Class In a first class lever the fulcrum is in the middle and the resistance and effort is on either side Think of a *see-saw

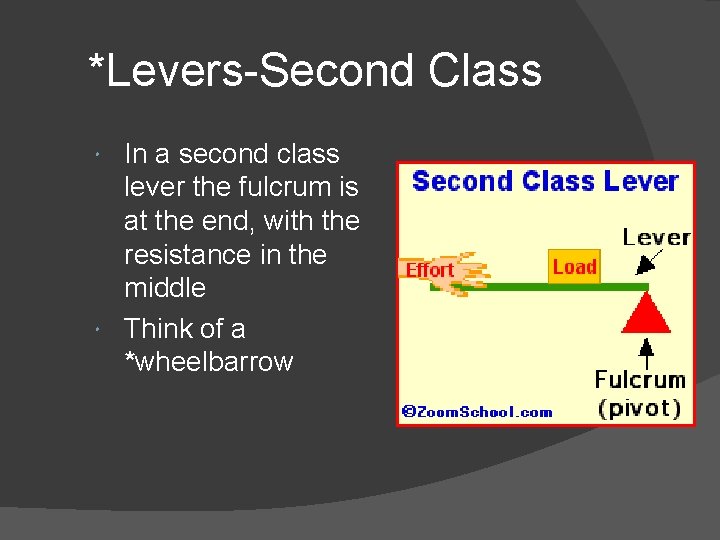
*Levers-Second Class In a second class lever the fulcrum is at the end, with the resistance in the middle Think of a *wheelbarrow

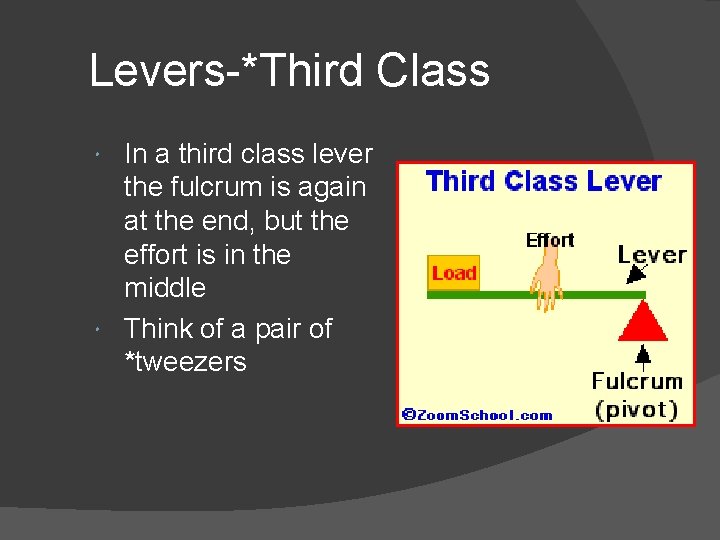
Levers-*Third Class In a third class lever the fulcrum is again at the end, but the effort is in the middle Think of a pair of *tweezers

st 1 Class nd 2 Class – 3 rd Class – Effort (E) – Fulcrum (F) Resistance (R)

Levers make work easier by reducing the amount of force necessary to move a load. Mechanical Advantage of a lever is equal to effort arm divided by the resistance arm. MA = effort resistance

Lever Family 2. PULLEY

Pulleys The pulley distributes the force of the load among several ropes in the system Using a single pulley does not multiply the input force, but it does change the direction of the input force. Using several pulleys increases the distance the of the input force causing a larger output force. The mechanical advantage is equal to the number of ropes sharing the load. MA = # of ropes-1 or MA = # of pulleys Figure 3 pg 440

Lever Family 3. WHEEL AND AXLE

Wheel and Axle A wheel and axle system makes work easier by increasing a small amount input force applied to the wheel. Mechanical Advantage is the wheel radius divided by the axle radius. MA = radius wheel radius axle

The Inclined Plane Family Inclined plane Wedge Screw

Inclined Plane Family 4. INCLINED PLANE

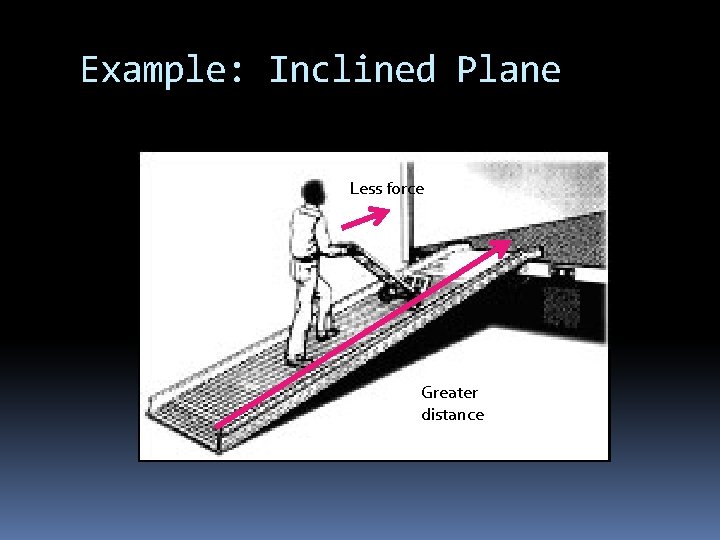
Inclined Plane An inclined plane makes work easier by increasing the distance over which force is applied. Less input force is required to lift a load. Mechanical Advantage of an inclined plane is equal to the distance of the sloped edge divided by the height. MA = slope height

Inclined Plane Family 5. WEDGE

Wedge A wedge is two inclined planes put back to back. Mechanical Advantage of a wedge is the slope length divided by the width of the wedge. MA = slope width

6. SCREW

Screw A screw is an inclined plane wrapped around a cylinder. Mechanical Advantage of a screw is length of the treads divided by the diameter of the cylinder. MA = length diameter

MA = F out F in MECHANICAL ADVANTAGE = LOAD EFFORT

WORK & MACHINES

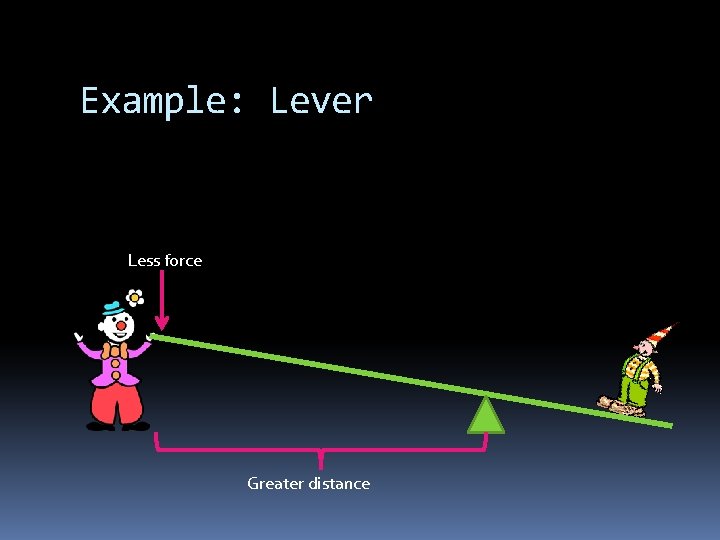
How do machines make work easier? By changing the size or direction of the FORCE Machines DO NOT make work less Force is less, therefore distance is greater W=F d

Example: Lever Less force Greater distance

Example: Inclined Plane Less force Greater distance

Work input (Win) The work that the operator/user does to the machine Input force (Fin)—force exerted by the user Input distance (din)—distance covered by the user Win = Fin x din

Work output (Wout) The work that the machine does to another object Output force (Fout)—force exerted by the machine Output distance (dout)—distance covered by the machine Wout = Fout x dout

Hints for solving problems Input Force is always less than Output force (Fin < Fout) Input distance is always greater than the output distance (din > dout)

Mechanical Advantage (MA) How much a machine multiplies force or distance Should always be greater than 1 (or it isn’t a very good machine!)

Equation MA = Fout Fin or MA = din dout

Sample Problem #1 A bus driver applies a force of 55. 0 N to the steering wheel, which in turn applies 132 N of force to the steering column. What is the mechanical advantage of the steering wheel? What simple machine is being used here? If the bus driver turns the wheel 1. 40 meters, how much work does she do?

G U E S S

Sample Problem #2 Two moving men are pushing a 225 N bookcase into the back of a moving truck by exerting 75. 0 N of force. The ramp is 3. 00 meters long and rises 1. 00 meters to the inside of the truck. A) How much work do the men do? B) How much work does the ramp do? C) What is the mechanical advantage of the ramp?

G U E S S

Review Why do we use simple machines? Simple machines are used to make work easier. List the two equations for Mechanical Advantage MA = F out / F in MA = d in / d out

Thursday, October 3, 2013 BR: When you calculate Mechanical Advantage, who is responsible for Input Output EQ: A student helps his teacher by lifting a heavy box, carrying it across the room, and putting it on the lab table. Did the student do work? When? Agenda: Work and Power Lab

Review When you calculate Mechanical Advantage, who is responsible for Input Output A student helps his teacher by lifting a heavy box, carrying it across the room, and putting it on the lab table. Did the student do work? When? Yes, only when lifting the box because his net force and the movement were in the same direction.

Review Work Power

Review 6 Simple Machines Mechanical Advantage

Review BR: What is in the middle of each class of lever? 1 st 2 nd 3 rd EQ: What are the appropriate equations and units for work and power? Work = F x d (Joules) Power = Work / time (watts)

SP 3. Students will relate transformations and flow of energy within a system. a. Identify energy transformations within a system (exmp. Lighting of a match. )

Key Concepts Vocabulary • There are many different forms of energy • Energy can change from one form to another • Energy • Law of conservation of energy

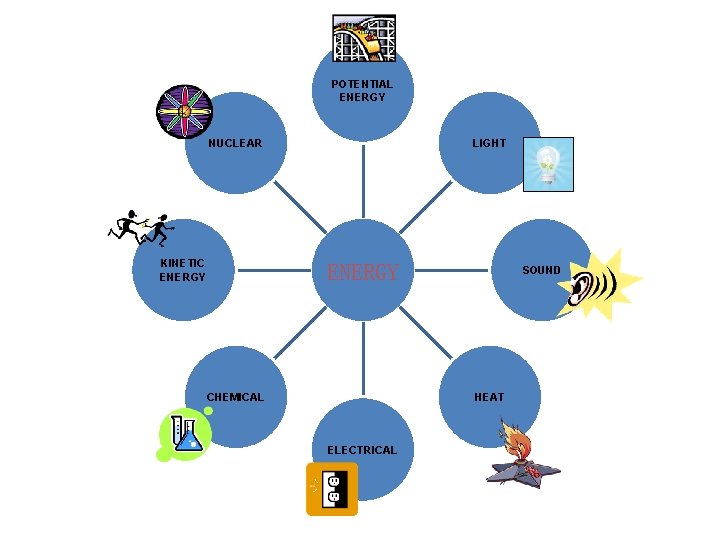
POTENTIAL ENERGY NUCLEAR KINETIC ENERGY LIGHT ENERGY CHEMICAL SOUND HEAT ELECTRICAL

Energy may change from one form to another, but total amount of energy in a system never changes.

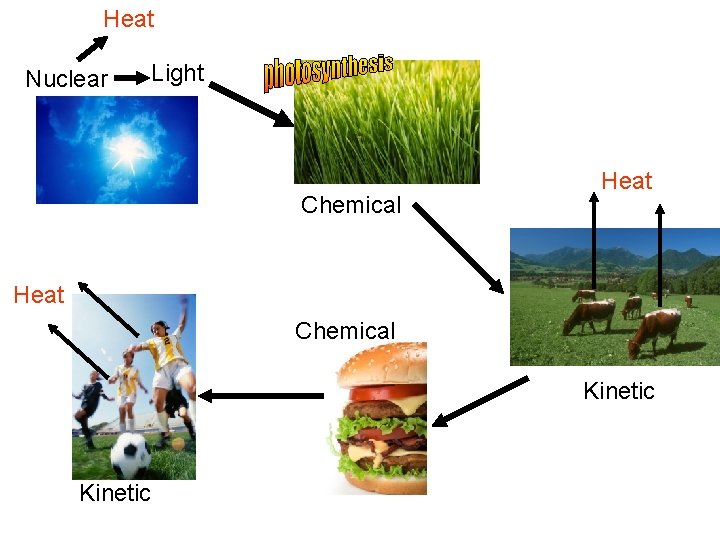
Examples of Energy Transformations • Burning a match – Chemical energy light, heat

• Bouncing a ball – Potential energy kinetic energy, sound, and heat


Examples • Photosynthesis – Light chemical energy

What energy transformations take place in the following scenario? A local farmer raises cattle for beef. On Friday night, you go out to your favorite restaurant and eat a hamburger.

Heat Nuclear Light Chemical Heat Chemical Kinetic

Review What forms of energy do you encounter each day? What energy transformations take place regularly in your everyday life?

Group Potential Energy-Calculate the gravitational potential energy of the following: A 1, 200 kg car at the top of a hill that is 42 m high. A 65 kg climber on top of Mount Everest (8, 800 m G U E S S high).

Group Potential Energy-Calculate the gravitational potential energy of the following: A 0. 52 kg bird flying at an altitude of 550 m. G U E S S

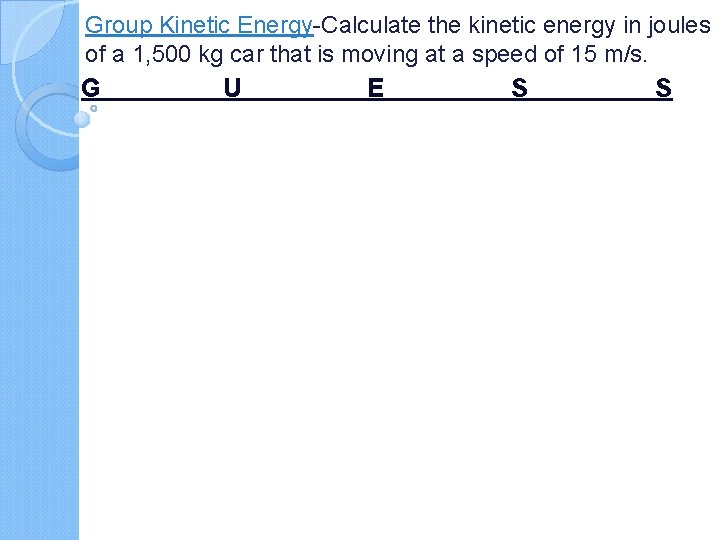
Group Kinetic Energy-Calculate the kinetic energy in joules of a 1, 500 kg car that is moving at a speed of 15 m/s. G U E S S

Review Kinetic energy is displayed while an object is __ ____. IN MOTION List the equation for calculating Kinetic Energy and provide the appropriate triangle. KE = ½ mv 2

Review Potential energy is displayed due to an object’s ____. POSITION List the equation for calculating Potential Energy and provide the appropriate triangle. PE = mgh

Review Answer the following based on yesterday’s lab When you drop a ball, where does it have the greatest amount of . . . • Potential energy? At the top just before it is released • Kinetic energy? At the bottom just as it hits the ground List the equation for calculating velocity using Kinetic Energy. . KE . V = (1/2)m

Review A skydiver prepares to jump out of a plane. At what point will she have the greatest kinetic energy? potential energy? The greatest kinetic energy occurs at the lowest point-just before she reaches the ground. The greatest potential energy occurs just at the highest point-just before she begins to jump out of the plane Describe the energy transformation-Ms. Berrie turns her projector on and shows the movie “Osmosis Jones” to her students. Electrical light + sound

Energy Problems Energy Test. Calculating Velocity

Additional Group Practice You drop a 2 kg watermelon from a 5 m tall ladder. How fast is the melon traveling when it strikes the ground? G U E S S

Additional Group Practice You drop a 0. 250 kg baseball from a height of 6 m. How fast is the ball traveling when it strikes the ground? G U E S S

Additional Group Practice After 10 s of free-fall, a 70 kg skydiver has 30. 5 J of kinetic energy. How fast is he traveling towards earth at that instant? G U E S S

Additional Group Practice After 120 s of free-fall, the same 70 kg skydiver has 220 J of kinetic energy. How fast is he traveling towards earth? G U E S S

Individual Practice v. How fast is a 0. 35 kg ball traveling as it hits the ground if it is dropped a total distance of 2 m? v. A 30 kg cannon ball is shot from a cannon and reaches a maximum of 410 J of kinetic energy. How fast is it travelling at that particular moment? v. A welder working on a new office building drops his construction hat as he reaches the top of the 50 m building. If the mass of the hat is 1. 5 kg, how fast is the hat travelling

Review BR: Based on the law of conservation of energy, what do you know about the total potential energy at the top of a fall and the total kinetic energy at the bottom of a fall? The total amount of energy remains the same. PE top = KE bottom EQ: Describe the following energy transformation: Mrs. Molyson drinks a cup of Gatorade then runs a 5 k. Chemical Kinetic

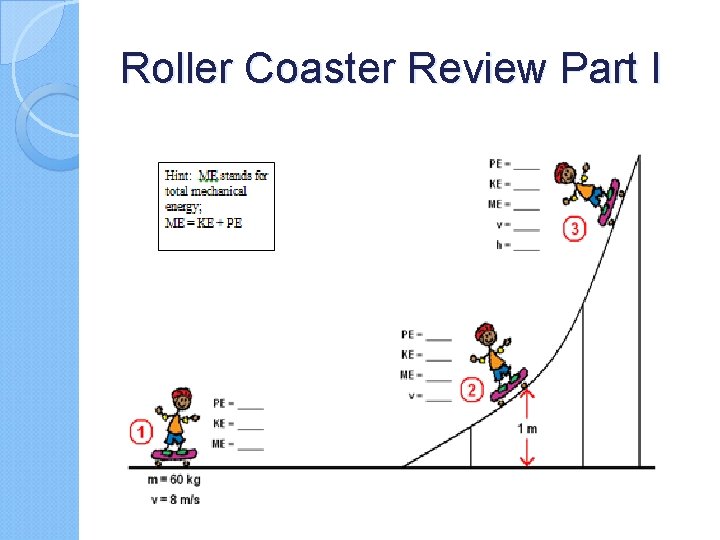
Roller Coaster Review Part I

Review Based on the law of conservation of energy, what do you know about the total potential energy at the top of a fall and the total kinetic energy at the bottom of a fall? The total amount of energy remains the same. PE top = KE bottom Describe the following energy transformation: Mrs. Molyson drinks a cup of Gatorade then runs a 5 k. Chemical Kinetic

Study Guide: Work, Power, Machines, Energy

Equations Work Power Mechanical Advantage Kinetic Energy Potential Energy

Review List the 3 requirements for work. Force 2. Distance 3. F & d must be in the same direction. 1.

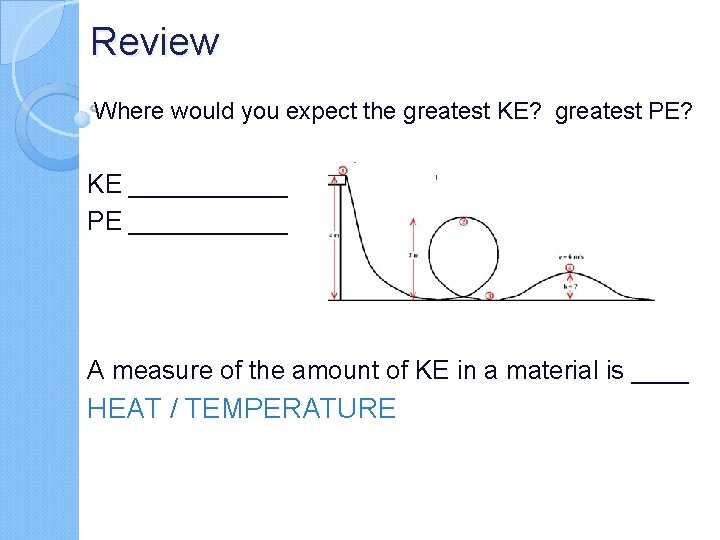
Review Where would you expect the greatest KE? greatest PE? KE ______ PE ______ A measure of the amount of KE in a material is ____ HEAT / TEMPERATURE

Tuesday, October 21, 2014 Agenda: Ø Ø Temperature & Heat Notes Temperature Conversions Practice Problems Ø Heat Transfer Notes Br: What state of matter has the least Kinetic Energy? Since solid particles move the slowest, the solid state of matter has the least amount of KE. EQ: What is the difference between 0 K versus 00 c and 00 F?

SPS 7 Relate transformations and flow of energy with a system. b. Investigate molecular motion as it relates to thermal energy changes in terms of conduction, convection, and radiation. 99


Why are terms such as “hot” and “cold” not good descriptions of temperature?

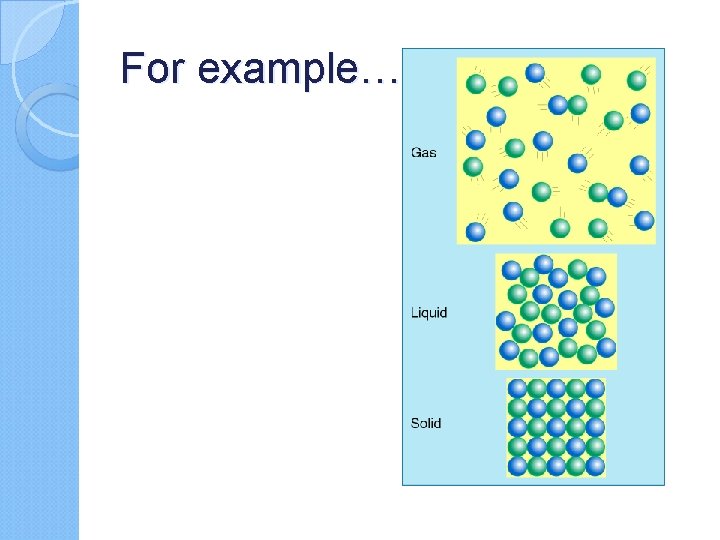
Kinetic Energy All substances (solids, liquids, and gases) contain particles Particles are constantly moving The temperature of a substance is proportional to the kinetic energy of its particles

For example…

solid gas liquid Which one has the lowest temperature? Which one has the highest temperature?

Temperature can be measured with a thermometer

How does a thermometer work? As substance is heated, particles move faster, bump into each other and spread out.

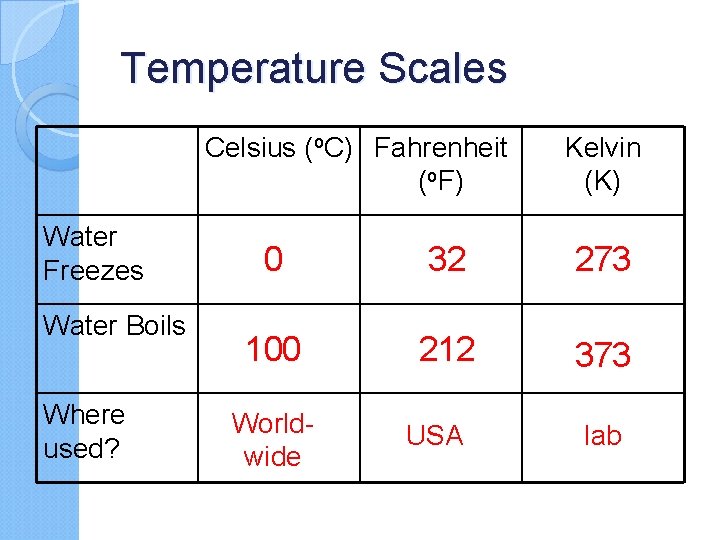
Temperature Scales Celsius (o. C) Fahrenheit (o. F) Water Freezes Water Boils Where used? Kelvin (K) 0 32 273 100 212 373 Worldwide USA lab

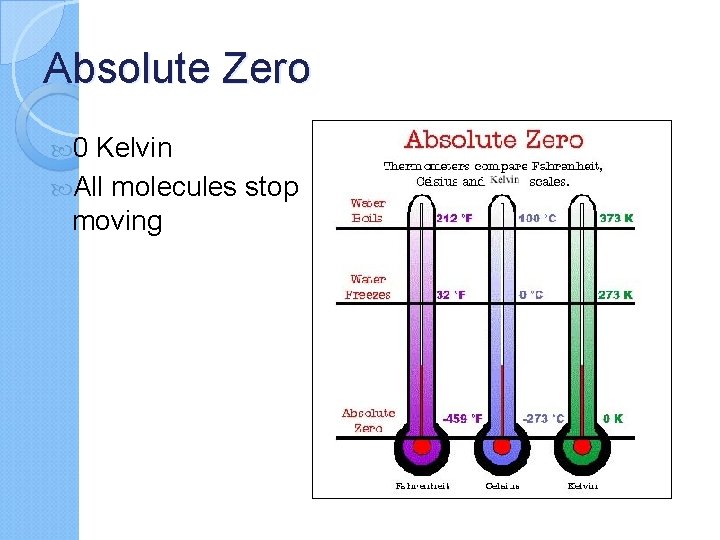
Absolute Zero 0 Kelvin All molecules stop moving

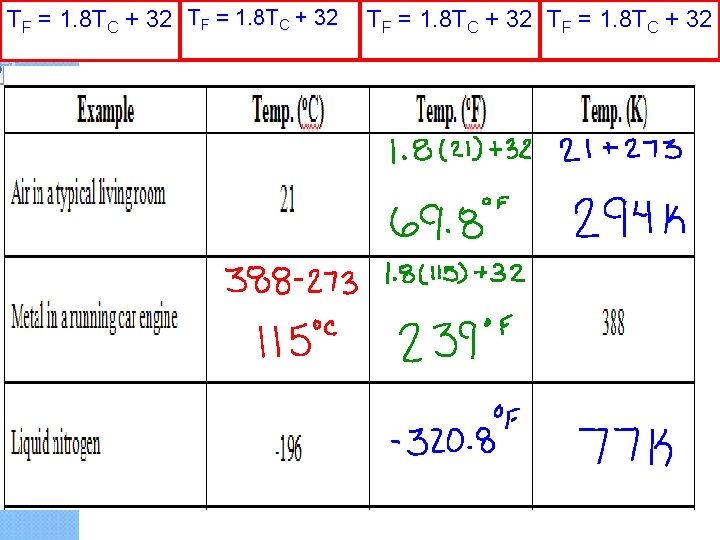
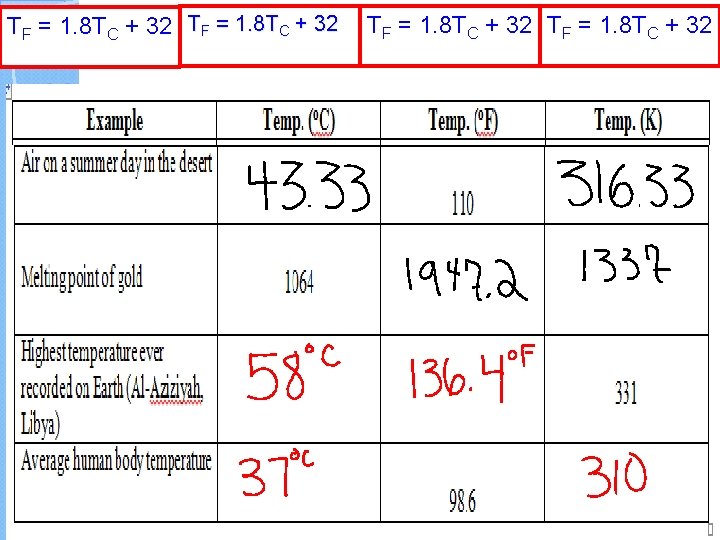
Temperature Conversion Equations Celsius to Fahrenheit TF = 1. 8 TC + 32 Fahrenheit to Celsius TC = (TF - 32) 1. 8 Celsius to Kelvin TK = TC + 273 Kelvin to Celsius TC = TK - 273

TF = 1. 8 TC + 32

TF = 1. 8 TC + 32

Tuesday, October 21, 2014 Agenda: Ø Ø Temperature & Heat Notes Temperature Conversions Practice Problems Gather your old BR/EQ. Get a new BR/EQ. You will need a periodic table to complete today’s work. Br: What state of matter has the least Kinetic Energy? Since solid particles move the slowest, the solid state of matter has the least amount of KE. EQ: What is the difference between 0 K versus 00 c and 00 F? 0 K is “Absolute Zero”. There is no particle movement at this temperature. Heat Assessment Next Tuesday 11/5

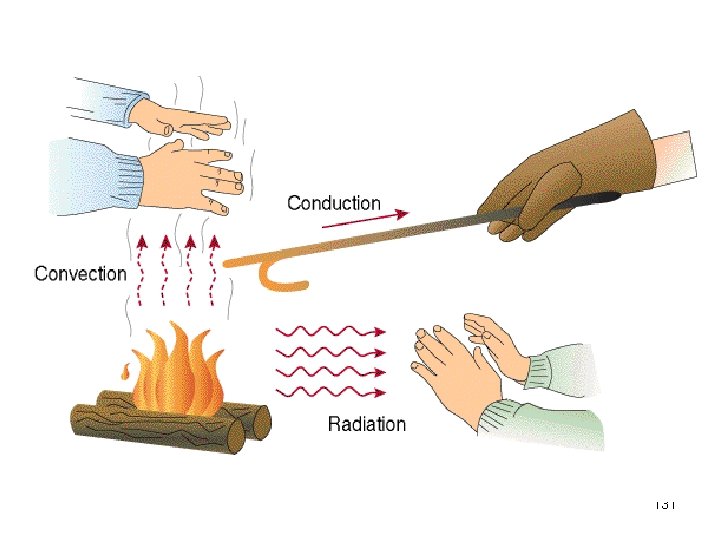
Heat Transfer Conduction Convection Radiation 11 3

Big Idea: How are the 3 methods of heat transfer similar? How are they different? 114

Thermal Equilibrium • Heat energy flows from the higher temperature to lower temperature 115

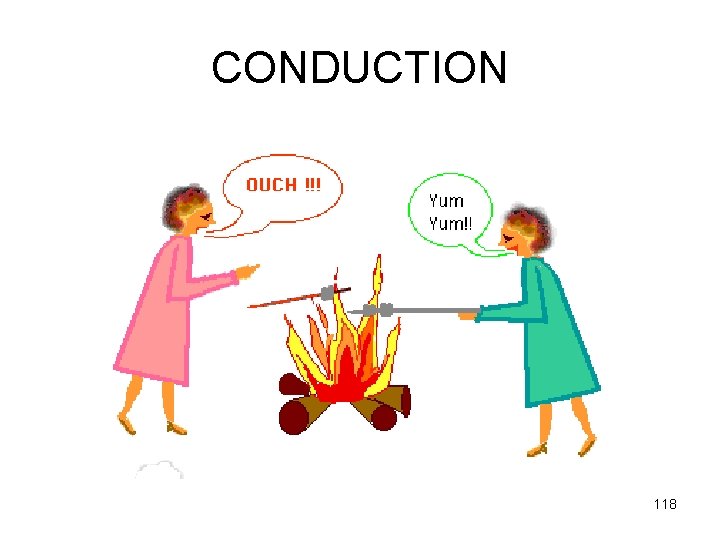
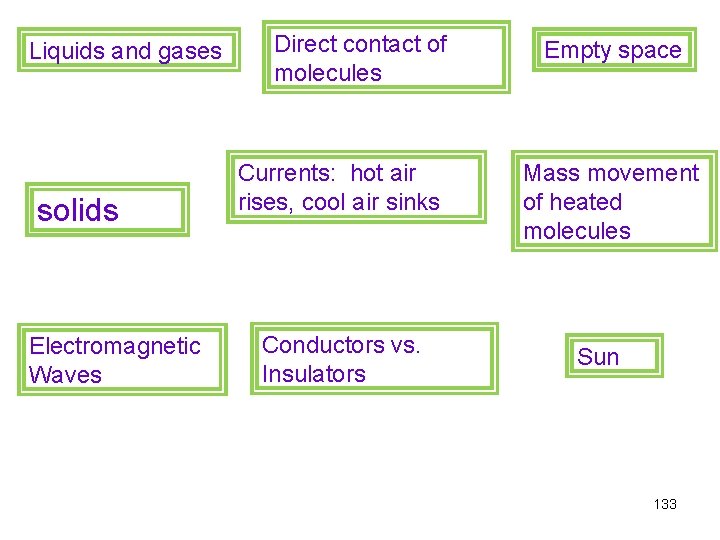
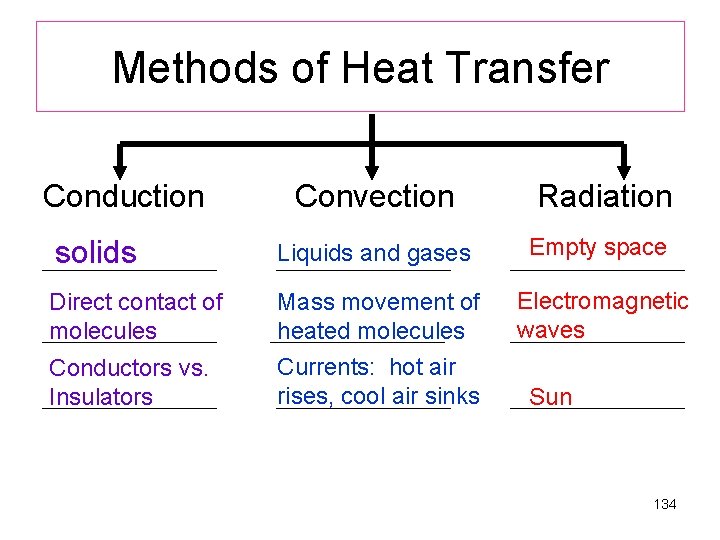
Conduction • Heat moves by direct contact of molecules • Most common in solids 116

Conductors vs. Insulators • Conductor: allows heat to move easily • Insulator: does not allow heat to move easily 117

CONDUCTION 118

CONDUCTOR OR INSULATOR? ? 119

Wooden Spoon 120

Frying Pan 121

Jacket 122

Metal Spoon 123

Styrofoam 124

AIR? 125

Air is a great insulator! 126

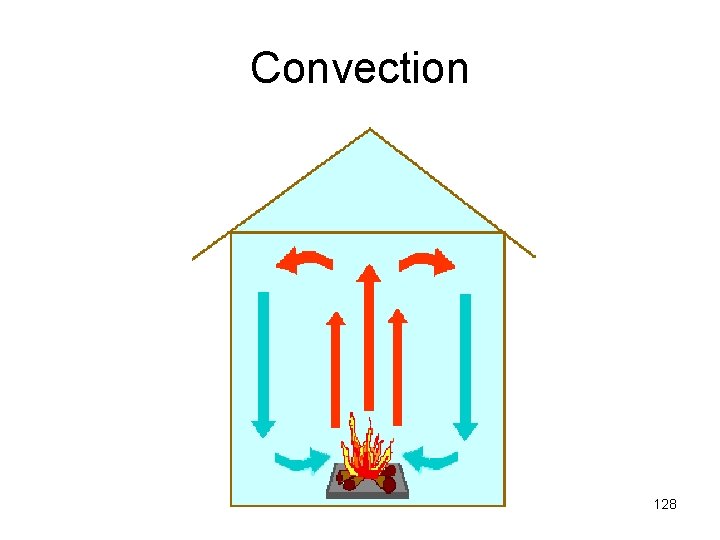
Convection • • Movement of heated substance Liquids and gases Creates currents Warm air expands and rises 127

Convection 128

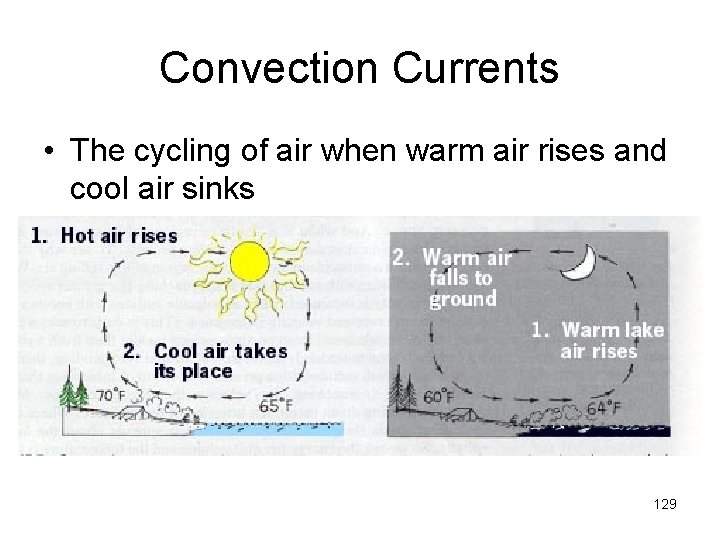
Convection Currents • The cycling of air when warm air rises and cool air sinks 129

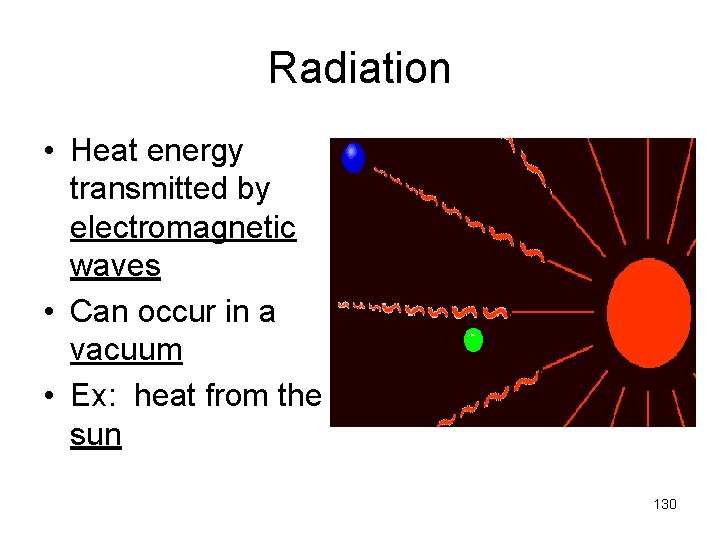
Radiation • Heat energy transmitted by electromagnetic waves • Can occur in a vacuum • Ex: heat from the sun 130

131

Create a tree map for the 3 methods of heat transfer: v. Conduction, Convection, & Radiation v. Include important information v. Include relevant pictures v. Make your map visually attractive Reference: 480 in the textbook. 132

Liquids and gases solids Electromagnetic Waves Direct contact of molecules Currents: hot air rises, cool air sinks Conductors vs. Insulators Empty space Mass movement of heated molecules Sun 133

Methods of Heat Transfer Conduction Convection Radiation solids Liquids and gases Direct contact of molecules Mass movement of heated molecules Currents: hot air rises, cool air sinks Conductors vs. Insulators Empty space Electromagnetic waves Sun 134

Methods of Heat Transfer Conduction Cup of coffee Convection Radiation Night and Day Candle Room Candle and metal Beaker Candle and stick Radiator Bulb Sun and Earth Camp fire 135

What is the freezing point of water in each temperature scale? Fahrenheit 32 0 F Celsius 0 0 c Kelvin 273 K What type of heat transfer does not require particles of matter? Radiation can travel through empty space.

Phase Change & Specific Heat 137

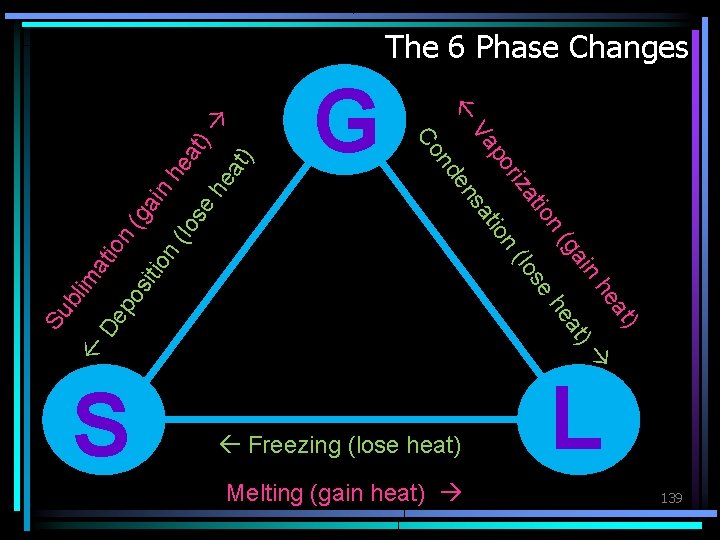
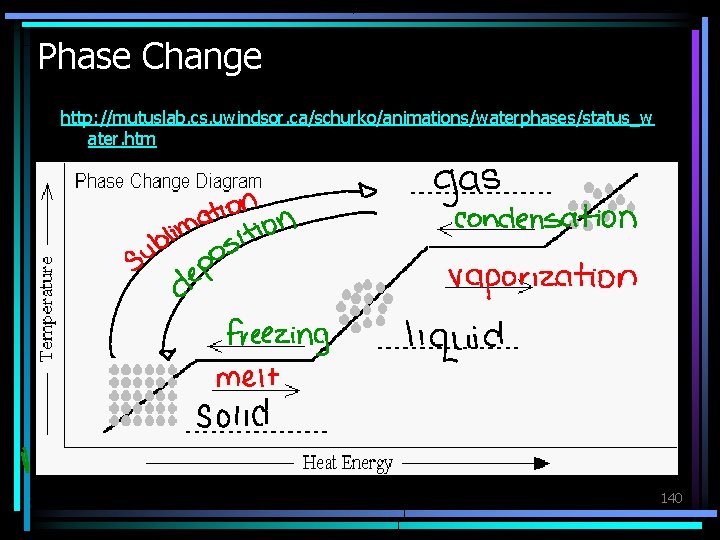
Phase Change What phase change is taking place in each of the following? • Melting – Solid to liquid • Freezing – Liquid to solid • Vaporization (boiling or evaporation) – Liquid to gas • Deposition – Gas to solid • Sublimation – Solid to gas • Condensation – Gas to liquid 138

V D lim Su b ) at ) at he he in a (g e os (l ion n tio t sa en iza or ap nd G Co at ion ep (g os ain itio n (lo hea se t) h ea t) The 6 Phase Changes L S Freezing (lose heat) Melting (gain heat) 139

Phase Change http: //mutuslab. cs. uwindsor. ca/schurko/animations/waterphases/status_w ater. htm 140

Specific Heat SPS 7 c. Determine the heat capacity of a substance using mass , specific heat, and temperature. 141

Specific Heat (c) • The amount of energy required to raise the temperature of 1 kilogram of a substance by 1 Kelvin • Measured in J/kg. K • Example: for water, c = 4, 186 J/kg. K 142

Specific Heat & Conductivity • Low specific heat values, show that heat is easily absorbed; which indicates the material is a better conductor. • High specific heat values, show that heat is not easily absorbed; which indicates the material is a better insulator. 143

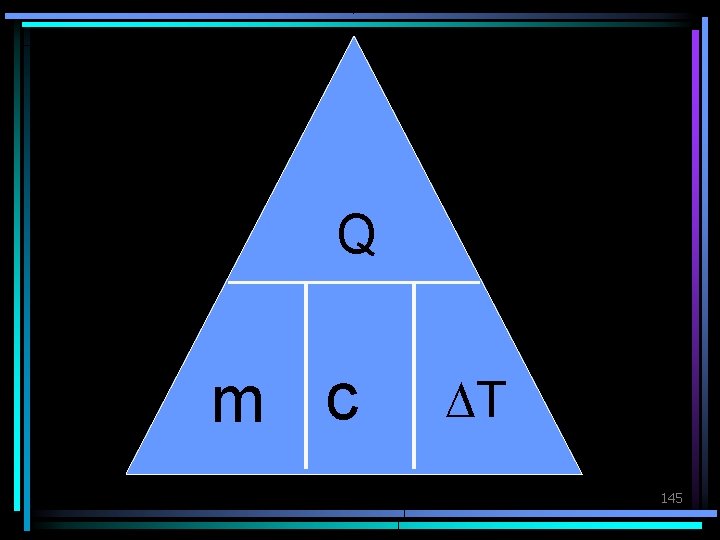
Calculating with Specific Heat Q = mc. DT Heat Energy Q: m: c: DT: (J) mass (kg) specific heat (J/kg. K) change in temperature (K) (final temp. -initial temp. ) 144

Q m c DT 145

Practice How much energy is needed to increase the temperature of 755 g of iron (c = 449 J/kg. K) from 283 K to 403 K? G m = 755 g = 0. 755 kg c = 449 J/kg. K DT = 403 K – 283 K = 120 K U Q=? 146
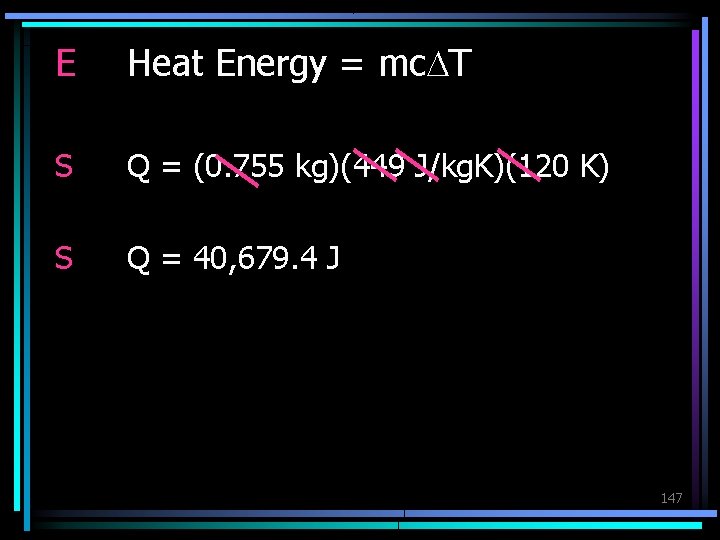
E Heat Energy = mc. DT S Q = (0. 755 kg)(449 J/kg. K)(120 K) S Q = 40, 679. 4 J 147

Which type of heat transfer requires that particles of matter touch? Conduction What is specific heat? The amount of energy required to raise the temperature of 1 kg of any substance 1 K.

A piece of lead absorbs 2500 Joules of heat and as a result its temperature rises from 50 o. C to 70 o. C. What is the mass of the piece of lead? (c of lead = 129 J/kg. K) • 0. 969 kg or 969 g 149

An aluminum baking sheet with a mass of 150 g absorbs 12, 000 J from an oven. If its temperature was initially 60 o. C, what will its temperature be after it is heated in the oven? (c of aluminum = 897 J/kg. K) • 422 K or 1490 c 150

Which type of heat transfer requires that particles of matter circulate? Convection Substance A has a specific heat of 3250 J/kg. K. Substance B has a specific heat of 425 J/kg. K. Which substance will make the better conductor? Substance B is a good conductor. A low specific heat means it will absorb heat easily.

• Celsius to Fahrenheit • Kelvin to Celsius TF = 1. 8 TC + 32 TC = TK - 273 • Fahrenheit to Celsius • Celsius to Kelvin TC = (TF - 32) 1. 8 TK = TC + 273 Q = mc. DT 152