Energy the Electron Unit 1 Atomic Structure Introduction

Energy & the Electron Unit 1 - Atomic Structure

Introduction In the study of the atom, there are some important concepts that can help you develop your understanding of matter. Ideas that we will investigate include: 1. The Wave & Particle Nature of Light (energy) 2. The Nature of Electrons in Atoms 3. Bonding 4. Trends in the Elements on the Periodic Table

Light as a Wave Fundamentals, Properties and Relationships in Light

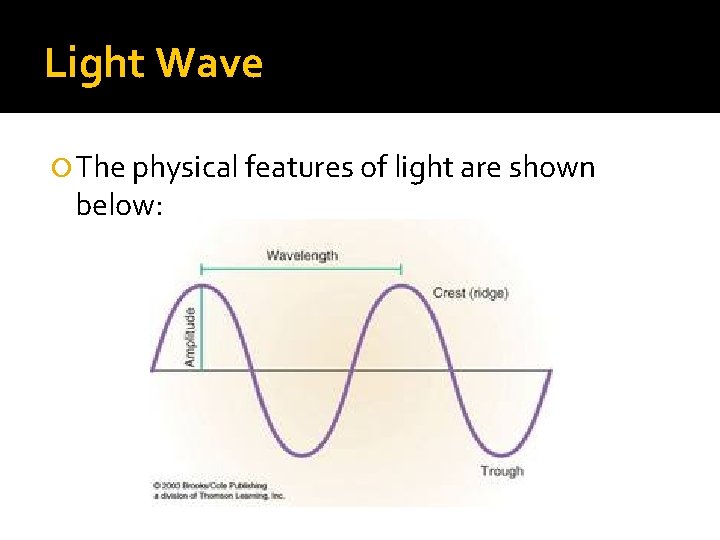
Wave Nature of Light is a form of energy and the light we see is part of the Electromagnetic (EM) Spectrum Light has wave properties, including: Wavelength (λ) – distance between consecutive crests or troughs in waves (measured in meters) Amplitude – height of the wave Frequency (f) – number of crests or troughs passing each second (measured in s-1 or Hertz) Speed (c) – for light being 3. 0 x 108 m/s

Light Wave The physical features of light are shown below:

Determining λ and ν There is a relationship between these properties of a wave. This is shown by the formula: c = fλ We can use this relationship to solve for either one of the wave characteristics.

Example: Calculate λ

Example: Calculate ν

Light as a Particle Light’s Alter Ego

Particle Nature of Light has both wave and particle properties (a dual nature) Why? Well…. The wave model does not explain the observations of why heated objects will only emit certain frequencies of light at a given temperature. Max Planck (1856 -1947) proposed that there needed to be a minimum amount of energy that can be gained, or lost, by an atom (this energy is called a quantum)

Planck’s Theory Planck determined a relationship for energy and the observations made: Equantum = hf Where h = 6. 626 x 10 -34 J·s Theory states that matter can only absorb or emit energy in whole number multiples of hf (1 hf, 2 hf, 3 hf, . . . ) i. e. No partial multiples

Applying Planck’s Theory We can use the formula, E = hν to solve for: 1. Energy of a particle, or the 2. Frequency of the particle Remember that h is a constant! Example: What is the amount of energy in a particle that has a frequency of 7. 76 x 1014 Hz? E = hf E = (6. 626 x 10 -34 J·s)(7. 76 x 1014 Hz) = 5. 14 x 10 -19 J

Applying Planck’s Theory (cont’d) Example: What is the energy of a particle that has a wavelength of 566 nm? This question is little bit of a different take on the problem, since it has two issues to overcome: 1. It provides λ instead of f, and 2. It states a wavelength in nm (nanometers)

What is a nanometer (nm)? A nano- anything means that the measure is actually a very small number. As a metric prefix, it stands for 10 -9. So, if we have 600 nm, it basically means: 600 x 10 -9 m, or: 6. 00 x 10 -7 m Note: you can enter the value as 600 x 10 -9 on your calculator and it will work, but you are expected to show the correct Scientific Notation value when writing it down.

Solution to Problem: So now that we have a way to fix the number, what do we do with it, since we actually need frequency? Any ideas? We can change wavelength to frequency using c=fλ. c = fλ = 5. 30 x 1014 Hz Remember that 566 x 10 -9 = 5. 66 x 10 -7

Now Solve for Energy:

Quantum Theory of the Atom Understanding the Atom and the Electron

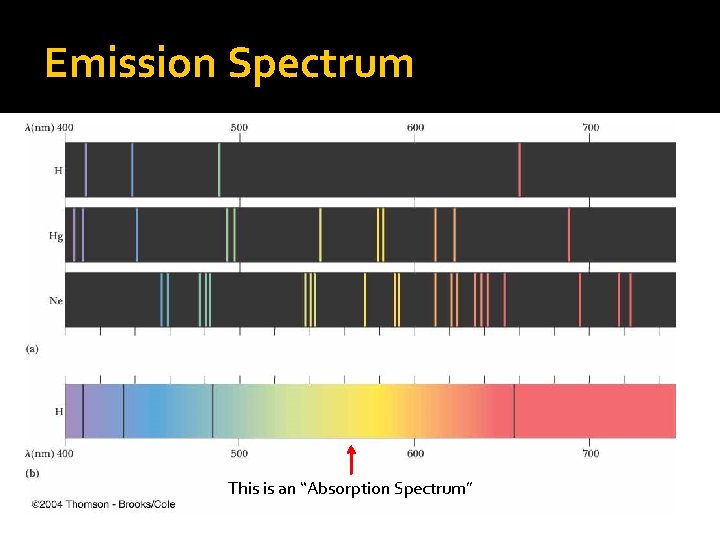
Emission Spectrum A neat property of the elements is that each element has a unique, what is called, “emission spectrum”. In a nutshell, an emission spectrum is a pattern of light radiation that is produced by an element after it has received energy (for example, being heated). This is an “Absorption Spectrum”

A Quantum Model of Hydrogen With the understanding that light has behaviour of both a particle and a wave, we can start to understand the emission spectra of atoms. One in particular, hydrogen (shown below) The theory of Planck and Einstein states that there are only certain allowable energy levels or states. The lowest allowable state is called the ground state.

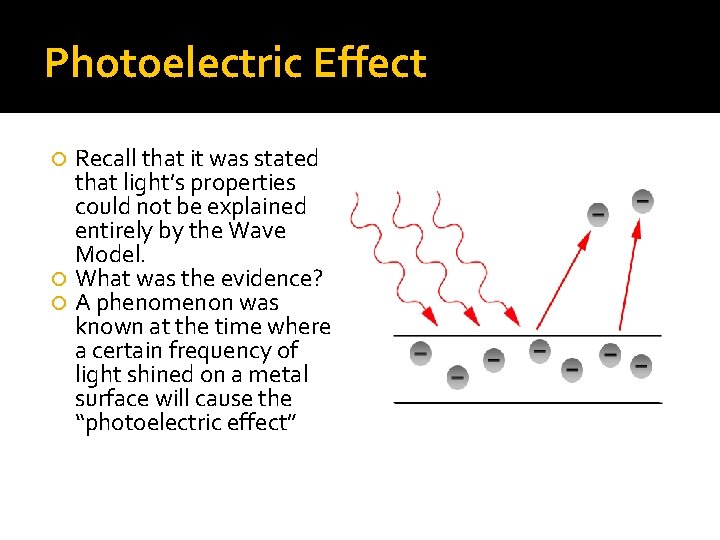
Photoelectric Effect Recall that it was stated that light’s properties could not be explained entirely by the Wave Model. What was the evidence? A phenomenon was known at the time where a certain frequency of light shined on a metal surface will cause the “photoelectric effect”

Particles of Light This effect results in the release of electrons from the metal. Due to this apparent ability of light to cause the ejection/excitation of electrons from a metal, Albert Einstein proposed that light existed as bundles of energy called “photons”

Atomic Emission Spectra Elements have the ability to absorb certain amounts of energy. When the atoms of an element absorb enough energy, they become “excited”. In this state it is actually the electrons that become excited. When these electrons release this energy to go back down to “ground” state, they release it in the form of radiation (light). Each element will display a particular emission spectrum, so we can actually identify elements by their emission spectrum.

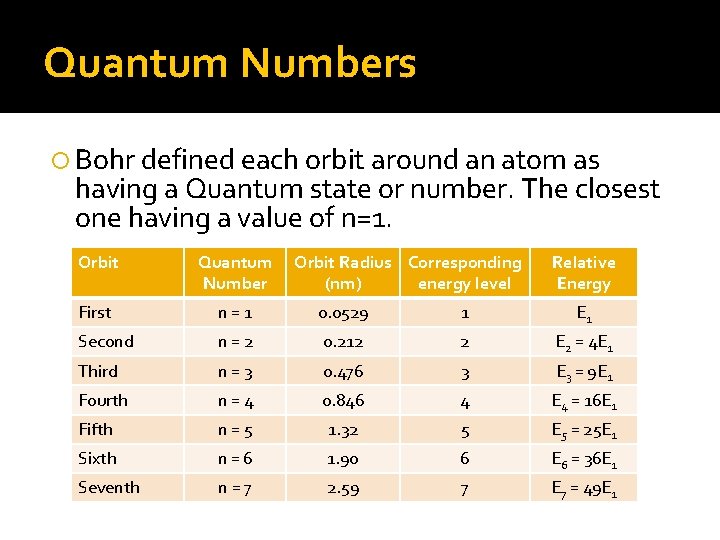
Energy States of Hydrogen Neils Bohr developed a model for an atom. He also developed a quantum model of hydrogen that helps explain the visible spectrum of hydrogen. Although hydrogen has only one electron, it can have many different excited states. There is a different energy level corresponding to each possible orbit around the atom (the lowest energy level for the orbit closest to the nucleus)

Quantum Numbers Bohr defined each orbit around an atom as having a Quantum state or number. The closest one having a value of n=1. Orbit Quantum Number Orbit Radius Corresponding (nm) energy level Relative Energy First n=1 0. 0529 1 E 1 Second n=2 0. 212 2 E 2 = 4 E 1 Third n=3 0. 476 3 E 3 = 9 E 1 Fourth n=4 0. 846 4 E 4 = 16 E 1 Fifth n=5 1. 32 5 E 5 = 25 E 1 Sixth n=6 1. 90 6 E 6 = 36 E 1 Seventh n=7 2. 59 7 E 7 = 49 E 1

Emission Spectra – Different Series The emission spectrum that we do see is only a part of what is released by the atom of hydrogen (the visible part is called the Balmer Series). There are 2 other Series corresponding to the ultraviolet range (Lyman) and infrared range (Paschen), which we cannot see. we can see what levels of electrons move from and to using the diagram on the next slide:

Emission Series

Does All Matter Act as both Particle and Wave? A scientist in the mid-1920’s by the name of de Broglie proposed that since waves can display particle-like behaviour, then particles can show wave-like behaviour. His idea developed into the following: λ= h mv Where: m = mass in kg and v = velocity in m/s What is the wavelength for a car of mass 910 kg and a velocity of 25 m/s? 2. 9 x 10 -38 m

Practice/Review Questions What is the frequency of green light with a wavelength of 540 nm? 5. 6 x 1014 Hz 2. How much energy in joules is there in light with a frequency of 4. 67 x 1017 Hz? 3. 09 x 10 -16 J 3. What is the wavelength of a Panther with a mass of 85 kg and a velocity of 12 m/s? 6. 5 x 10 -37 m 1.

Electrons & Bonding Study of the Configuration of the Atom’s Electrons

Electron Orbitals & Electron Configuration Heisenberg’s Uncertainty Principle states: Electrons are constantly moving. We cannot know both the precise location of an electron around an atom and its speed. Instead, we have a region called an “orbital” which indicates its most probable location. Each orbital can carry, at most, 2 electrons. There are 4 different types of orbitals: s, p, d, and f

Electron Configuration We use a special notation to write the electron configuration for an element that utilizes the s, p, d, and f orbital names. Each orbital type has a unique shape to account for the additional electrons.

Using the s, p, d, and f Notation This is how it works: We start with s orbitals and go up to 2 We can then add p orbitals and go up to 6 Next are the d orbitals that go up to 10, then f orbitals to 14 Observe these examples: Starting with hydrogen, we know that it has only the 1 electron. Its electron configuration is 1 s 1. For helium, which has 2 electrons, its configuration is 1 s 2. For lithium, which has 3 electrons, its configuration is 1 s 22 s 1 (why? ) For boron, which has 5 electrons, its configuration is 1 s 22 p 1

Practice: Write the full electron configurations for the following elements: Carbon Fluorine Sodium

Electron Dot Diagrams Elements we know, have certain abilities to form chemical bonds. The number of bonds is based on the number of “valence” electrons for that element (the electrons in the outermost shell or orbital). We can illustrate this for each element by drawing what is called an “electron dot diagram”.

Basic Dot Diagrams Here is how Dot Diagrams are drawn: We place electrons around the 1. Hydrogen H • symbol (in no particular order). 2. Helium 3. Lithium 4. Beryllium 5. Boron • He • • Li • • • Be • • B • • We add new electrons to a spot where there is no electrons until the element is surrounded. We now add electrons to form pairs. We add electrons until all electrons are paired.

Drawing a Dot Diagram In order to determine the number of valence electrons that an element has, we need to use the electron configuration for that element. The number of valence electrons is equal to the number of electrons found in its highest orbital (“principal quantum number”). For example: Sn (tin) has 50 electrons its electron configuration is: [Kr]5 s 24 d 105 p 2 So Sn has 4 valence electrons • • Sn • •

Electron Box Diagrams: Ground State Electron Configuration Recall that ground state is the lowest possible energy state for an element (and its electrons) The arrangement of an element’s electrons is dictated by three rules or principles: Aufbau Principle – each electron occupies the lowest energy orbital possible. Pauli Exclusion Principle – two electrons may occupy the same orbital as long as they have opposite “spins”. Hund’s Rule – states that electrons must fill empty orbitals before pairing electrons of opposite spin.

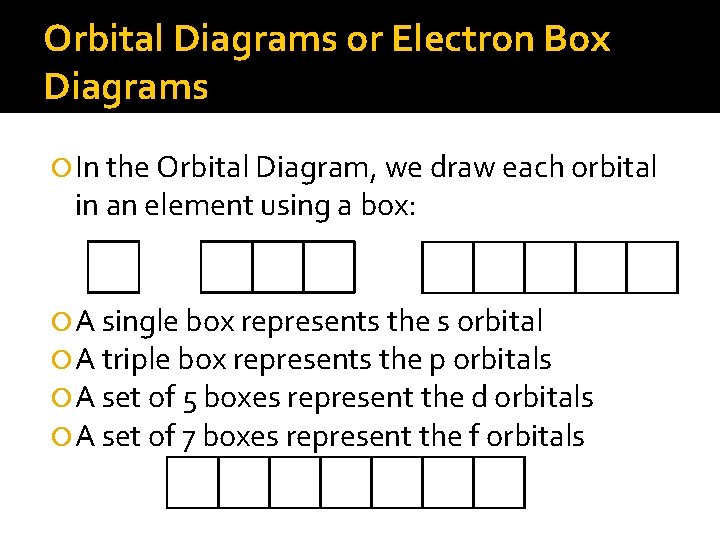
Orbital Diagrams or Electron Box Diagrams In the Orbital Diagram, we draw each orbital in an element using a box: A single box represents the s orbital A triple box represents the p orbitals A set of 5 boxes represent the d orbitals A set of 7 boxes represent the f orbitals

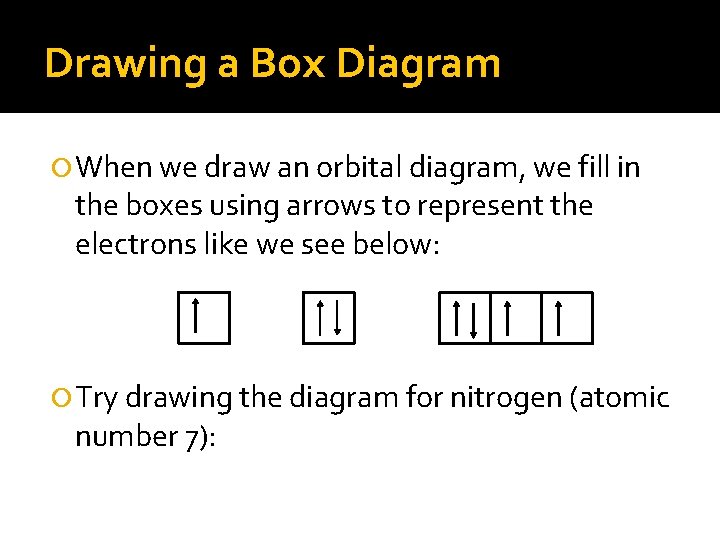
Drawing a Box Diagram When we draw an orbital diagram, we fill in the boxes using arrows to represent the electrons like we see below: Try drawing the diagram for nitrogen (atomic number 7):

Chemical Bonding & Orbitals Covalent chemical bonding is based on the number of valence electrons that are available to form that bond for the element. We are used to elements having the ability to form bonds like with carbon, where it can form up to 4 bonds (one for each valence electron). The standard rule for bond formation is to complete what is called an “octet” (8 valence electrons). Another requirement that has been made necessary is the need for free electrons in order to form a chemical bond.

Influence of Orbitals How do orbitals affect bonding? Consider the following compound: Be. Cl 2 If you draw the box diagram for Be, you normally would get this: So you actually don’t have any free electrons to form bonds. So how is Be able to form bonds?

Hybridization of Orbitals How it works for many elements is what is called “hybridization of orbitals”. In this process, an element creates free electrons by forming a hybrid orbital. This occurs by combining orbitals of the same quantum number. For Be. Cl 2, we see this: We move one electron from the pair to the available space in the next orbital type

Hybrid Orbital Types In the previous example, Be actually changes its bonding orbital type to the combination of the orbitals combined: sp The naming is based on the type of orbitals combined and how many “boxes” are used in the formation of the hybrid. Other possible hybrid types: sp 2, sp 3 d, sp 3 d 2 What kind of orbitals would we need for Al. Cl 3? Draw the Box Diagrams for both the non-hybrid Al and a hybrid Al.

Molecular Shape and Hybridization Each chemical molecule will have a particular shape associated with it. Hybridization of orbitals will cause the formation of a variety of molecular shapes that are very interesting: Open your text to page 260. You will find a table showing a variety of chemical molecules and their known shape. The type of hybridization does influence the generated shape for that molecule.

Trends in the Periodic Table Studying the Properties of the Elements

Trends in the Periodic Table We know that the elements vary in their properties, however, the elements will display similarities as well. We know that elements within a Group will have the same chemical properties (react the same). Trends are also seen as we move through the elements both down a Group (column) as well as across the Periodic Table.

Properties of the Elements We will look at the following properties: 1. Atomic Radius ▪ This is the measure of the atom of an element from the center of its nucleus to the edge of its electron cloud. 2. Ionic Radius ▪ This is the measure of the ion-form of an element from its center to the edge of the its electron cloud. 3. Ionization Energy ▪ This is the measure of the amount of energy it takes to remove an electron from the atom of that element.

Properties (cont’d) 4. Electronegativity ▪ This is basically a relative measure of the strength of attraction for electrons in that element. The Trends: Atomic Radius – we see is that the radius of an atom will: ▪ Increase in size as we move down a Group (atoms get bigger, more electron levels/shells) ▪ Decrease in size as we move across the Period (due to a higher core charge, pulls the electrons closer)

Trends (cont’d) Ionic Radius – the ionic radius will: ▪ Increase as we move down a Group (the number of ▪ ▪ orbits increase just like in atoms). Decrease as we move across (same idea as before, core charge increases), until will change the type of ion (positive to negative), then the pattern resets. The key ideas here are that: 1. Negative ions are larger than their atom 2. Positive ions are smaller than their respective atom

Trends (cont’d) Ionization Energy pattern (cont’d) ▪ The highest ionization energies belong to the Noble Gases (since they will NOT want to lose them). ▪ The lowest belong to the elements that typically form positive ions (easily lose electrons). Ionization Energy will: ▪ Decrease as we move down a Group (electrons get further away from the nucleus). ▪ Generally increase as we move across a Period (towards the Noble Gases).

Trends (cont’d) Electronegativity – the strength of an atoms’ attraction towards electrons will generally: ▪ Increase as we move from left to right (Noble Gases have no affinity for electrons). ▪ Decrease as we move from top to bottom (along a Group). What is the role of electronegativity? These electronegativity values will dictate what kind of bond will form between the atoms.

Electronegativity and Bonding Remember that there are 2 main types of bonds: Covalent Ionic The way we use electronegativity is the difference between the values: If the difference is 1. 0 or less, it will be a covalent bond. If the difference is 2. 0 or more, it will be an ionic bond. If the difference is between 1. 0 and 2. 0, it will be covalent with some polar character

Unit One Summary: Atomic Structure 1. The Electromagnetic (EM) Spectrum 2. Energy of a Particle (Planck) 3. de Broglie Equation 4. Ground State vs. Excited Stated 5. Spectra of the Elements 6. Quantum Number 7. Electron Configuration 8. Electron Dot Diagrams

Unit Summary (cont’d) 8. Electron Box Diagrams 9. Hybridization of Orbitals 10. Trends in the Periodic Table ▪ Atomic Radius ▪ Ionization Energy ▪ Electronegativity