Energy principle The 1 st law of thermodynamics

Energy principle (에너지 법칙) The 1 st law of thermodynamics (열역학 제 1법칙) – “conservation of energy” (no appearance or disappearance of energy in a system, but conversion to different energy: heat to mechanical, mechanical to heat) Q: heat transferred to the system W: work done by the system Ep: potential energy Ek : kinetic energy Eu: internal energy, associated with motion of molecules (structure of atoms, chemical E, electrical E) By Reynolds transport theorem,

Classification of work Flow work – work done by pressure forces as the system moves through space Flow work of a CVi System flow work Shaft work – work other than flow work pump – work on the flow, E of flow increases, negative work (-) turbine – work done by the flow, E of flow decreases, positive work (+) For steady flow (E accumulation = “ 0”) and uniform velocity across section in a pipe

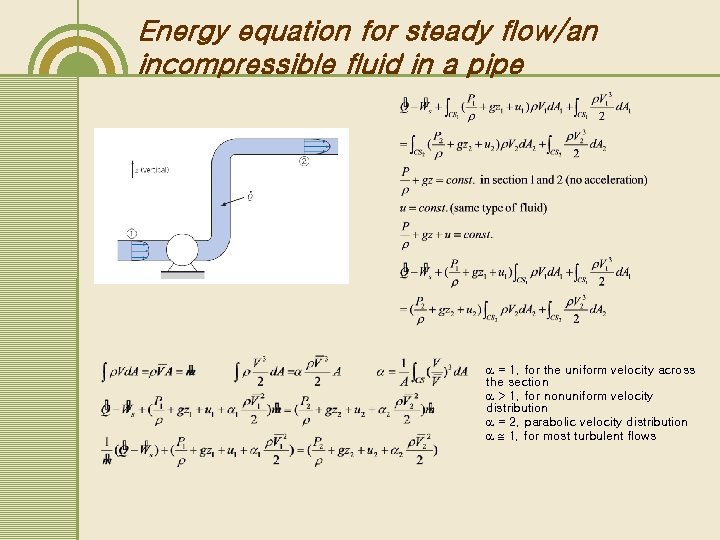
Energy equation for steady flow/an incompressible fluid in a pipe = 1, for the uniform velocity across the section > 1, for nonuniform velocity distribution = 2, parabolic velocity distribution 1, for most turbulent flows

Energy equation Shaft work(E consuming) – pump work on the flow (-, E supplying) and turbine work given by the flow (+, E consuming) Pump power Turbine power Power delivered by the pump to the flow Actual power delivered by the turbine

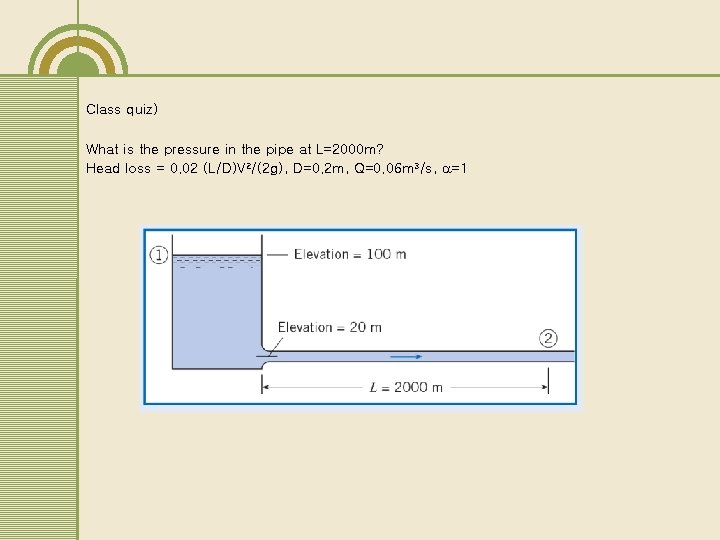
Class quiz) What is the pressure in the pipe at L=2000 m? Head loss = 0. 02 (L/D)V 2/(2 g), D=0. 2 m, Q=0. 06 m 3/s, =1

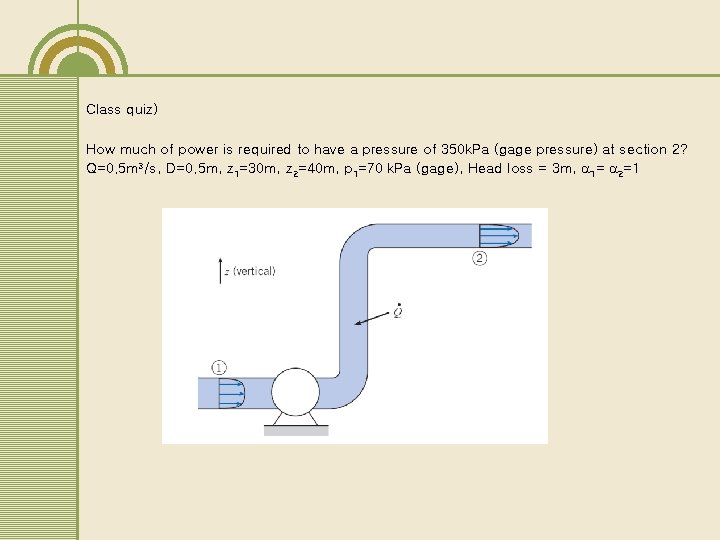
Class quiz) How much of power is required to have a pressure of 350 k. Pa (gage pressure) at section 2? Q=0. 5 m 3/s, D=0. 5 m, z 1=30 m, z 2=40 m, p 1=70 k. Pa (gage), Head loss = 3 m, 1= 2=1

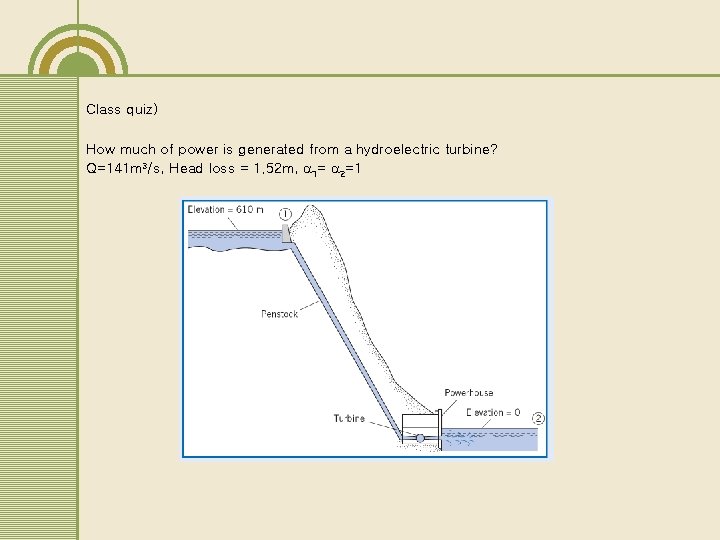
Class quiz) How much of power is generated from a hydroelectric turbine? Q=141 m 3/s, Head loss = 1. 52 m, 1= 2=1

Bernoulli equation - Energy equation Bernoulli equation – for a steady, incompressible, and inviscid flow along a streamline Energy equation – for viscous, incompressible flow in a pipe (with pumps and/or turbines) For the flow of inviscid (no head loss) in a small stream tube (uniform velocity distribution) and no pump and turbine, the Energy equation = the Bernoulli equation.

Class practice – Abrupt expansion Energy equation in the sections 1 and 2 (assumption, =1) Momentum equation in the sections 1 and 2 Continuity equation in the sections 1 and 2 If a pipe discharges liquid into a reservoir, V 2=0, and then

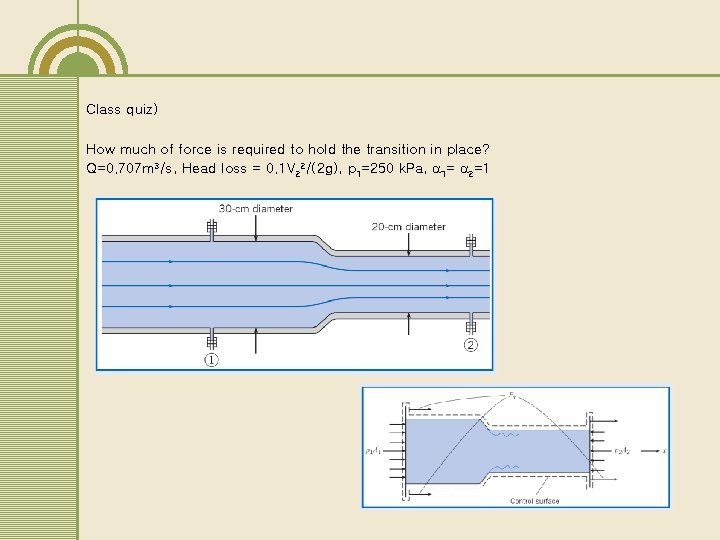
Class quiz) How much of force is required to hold the transition in place? Q=0. 707 m 3/s, Head loss = 0. 1 V 22/(2 g), p 1=250 k. Pa, 1= 2=1

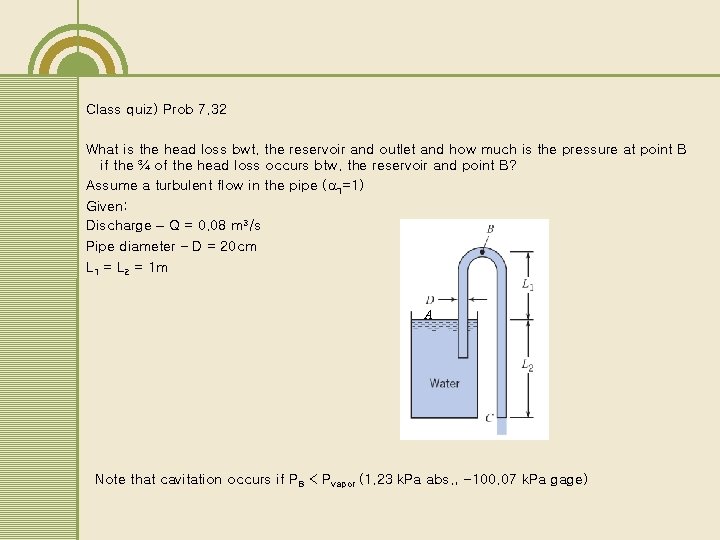
Class quiz) Prob 7. 32 What is the head loss bwt. the reservoir and outlet and how much is the pressure at point B if the ¾ of the head loss occurs btw. the reservoir and point B? Assume a turbulent flow in the pipe ( 1=1) Given: Discharge – Q = 0. 08 m 3/s Pipe diameter – D = 20 cm L 1 = L 2 = 1 m A Note that cavitation occurs if PB < Pvapor (1. 23 k. Pa abs. , -100. 07 k. Pa gage)

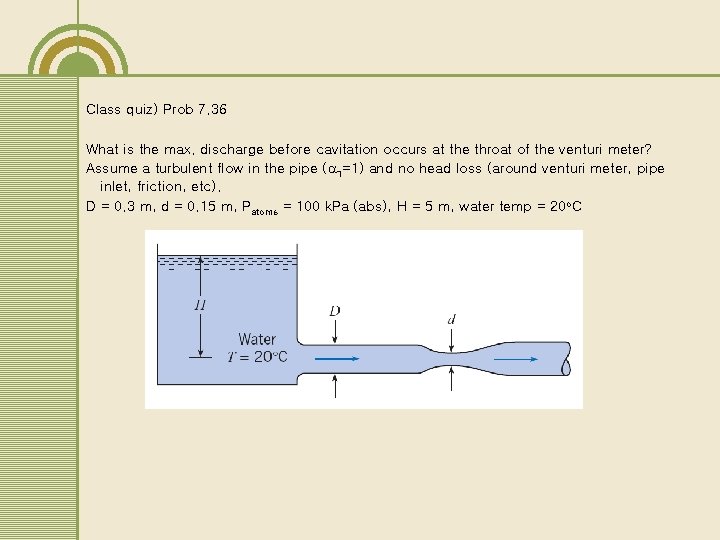
Class quiz) Prob 7. 36 What is the max. discharge before cavitation occurs at the throat of the venturi meter? Assume a turbulent flow in the pipe ( 1=1) and no head loss (around venturi meter, pipe inlet, friction, etc). D = 0. 3 m, d = 0. 15 m, Patoms = 100 k. Pa (abs), H = 5 m, water temp = 20 o. C

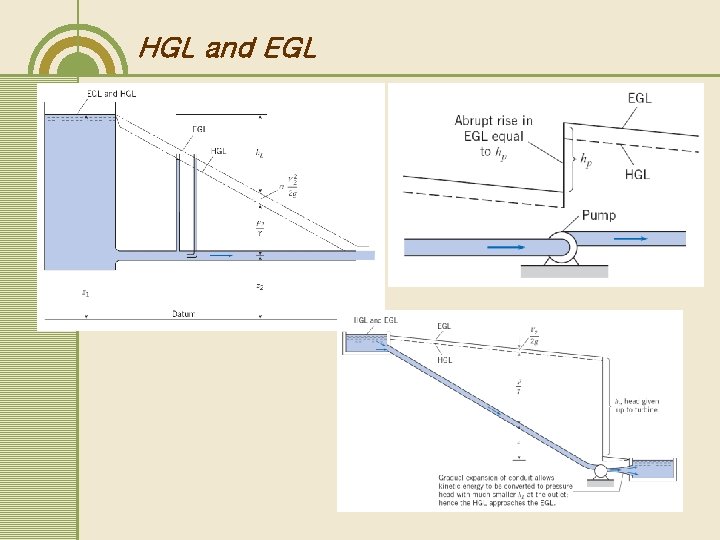
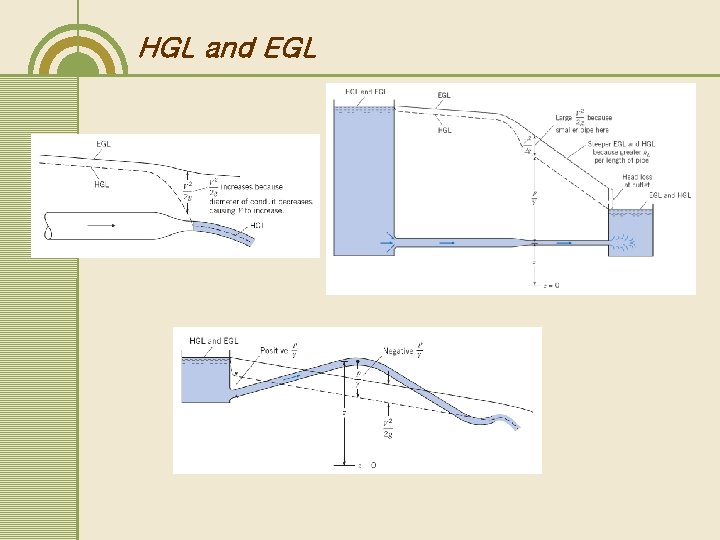
HGL and EGL Each term in the energy equation represents “energy per unit weight of the flowing liquid (N m/N)” in length unit (m)→ “Head” Hydraulic grade line (HGL, 동수경사선) – piezometric head (P/ +z) Energy grade line (EGL, 에너지경사선) – total head (P/ +z+ V 2/2 g) Remarks in EGL and HGL for a pipe • • EGL-HGL = V 2/2 g EGL=HGL at V=0 (reservoir surface) The downward slope in the direction of flow due to headloss The constant slope (= h. L/ L, head loss per unit length) of EGL for steady flow in a pipe of which physical characteristics are uniform (diameter, roughness, shape, etc. ) Abrupt rise given by a pump and abrupt drop given by a turbine in the EGL HGL = system line at p=0 in a pipe or channel (P/ =0) – outlet (to the atmosphere) and reservoir surface) Changes in pipe diameter → changes in EGL/HGL slopes If the HGL were below the pipe, there’s subatmospheric pressure in a pipe.

HGL and EGL

HGL and EGL

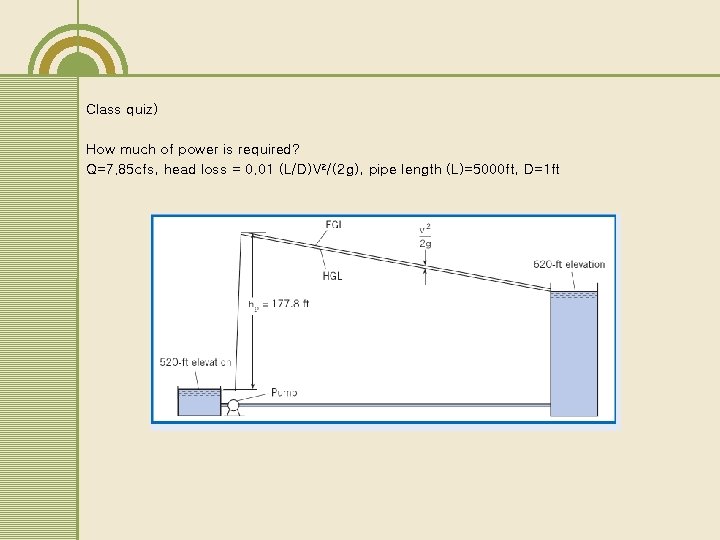
Class quiz) How much of power is required? Q=7. 85 cfs, head loss = 0. 01 (L/D)V 2/(2 g), pipe length (L)=5000 ft, D=1 ft

Class quiz) HGL and EGL

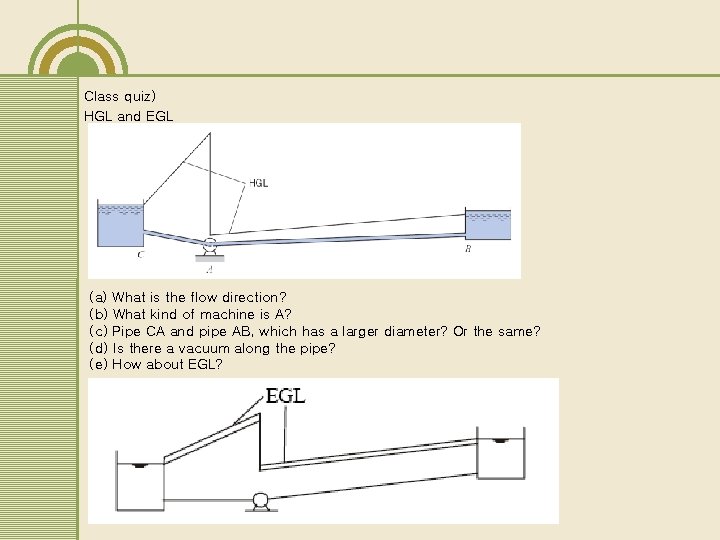
Class quiz) HGL and EGL (a) What is the flow direction? (b) What kind of machine is A? (c) Pipe CA and pipe AB, which has a larger diameter? Or the same? (d) Is there a vacuum along the pipe? (e) How about EGL?

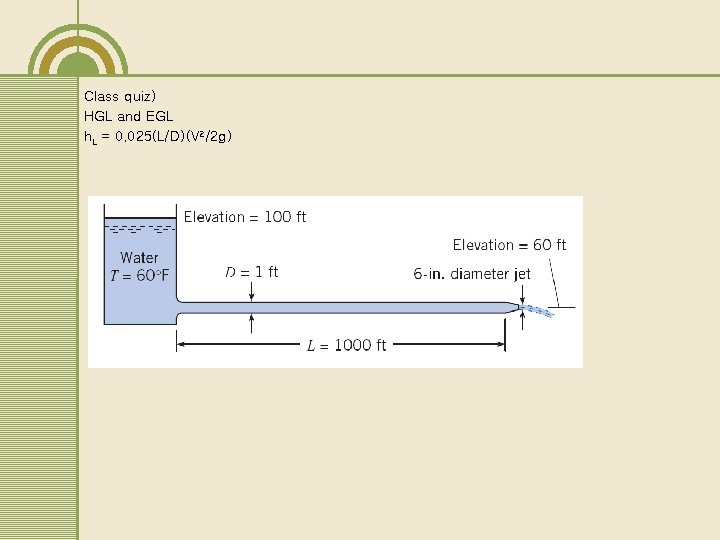
Class quiz) HGL and EGL h. L = 0. 025(L/D)(V 2/2 g)

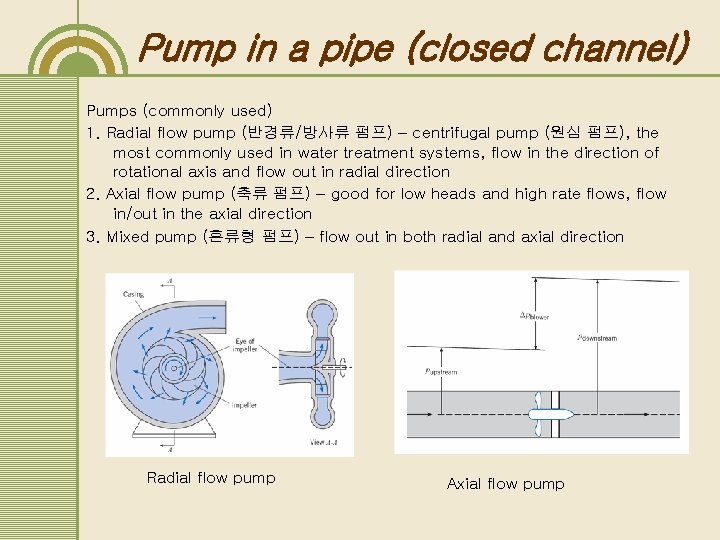
Pump in a pipe (closed channel) Pumps (commonly used) 1. Radial flow pump (반경류/방사류 펌프) – centrifugal pump (원심 펌프), the most commonly used in water treatment systems, flow in the direction of rotational axis and flow out in radial direction 2. Axial flow pump (축류 펌프) – good for low heads and high rate flows, flow in/out in the axial direction 3. Mixed pump (혼류형 펌프) – flow out in both radial and axial direction Radial flow pump Axial flow pump

Pump in a pipe (closed channel) Create an enough piezometric head (including head losses) to deliver a fluid from low elevation to high From the energy equation, For a system with one size pipe, the pump head (양정), The required head produced by a pump = elevation difference + all head losses Required pump power

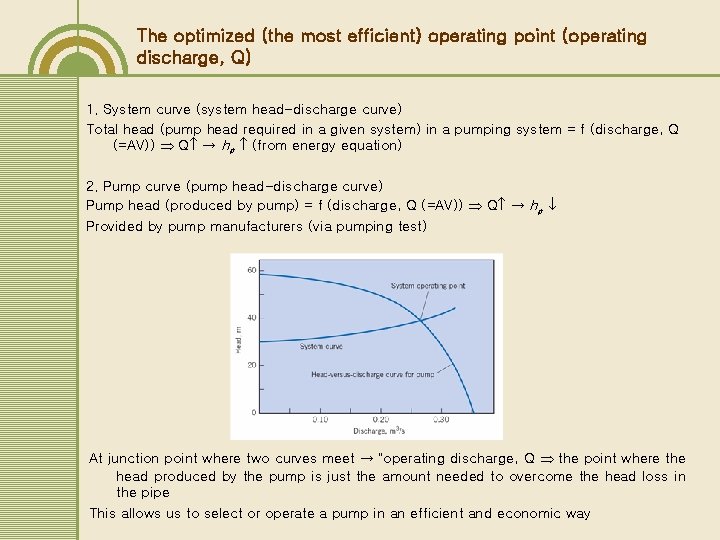
The optimized (the most efficient) operating point (operating discharge, Q) 1. System curve (system head-discharge curve) Total head (pump head required in a given system) in a pumping system = f (discharge, Q (=AV)) Q → hp (from energy equation) 2. Pump curve (pump head-discharge curve) Pump head (produced by pump) = f (discharge, Q (=AV)) Q → hp Provided by pump manufacturers (via pumping test) At junction point where two curves meet → “operating discharge, Q the point where the head produced by the pump is just the amount needed to overcome the head loss in the pipe This allows us to select or operate a pump in an efficient and economic way

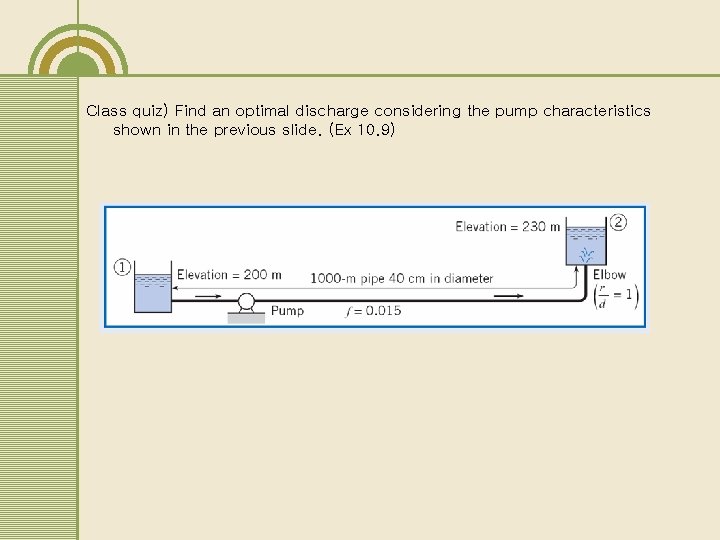
Class quiz) Find an optimal discharge considering the pump characteristics shown in the previous slide. (Ex 10. 9)

Net positive suction head (NPSH, 순양흡입수두) The pressure decreases at the suction side of a pump with increasing flow velocity (Bernoulli effect), which may result in a significant pressure drop, “cavitation”. NPSH = pressure head difference btw. the suction side of a pump and the vapor pressure head of a fluid pumped From energy equation btw. points 1 and 2 (suction side),

Net positive suction head (NPSH) The critical NPSH of a pump – determined by pump manufacturers via pumping test If NPSH < critical NPSH → cavitation Typically, critical NPSH values for centrifugal pumps ~ 3 m In the application of a given pump, if discharge (Q=AV), suction height (H), or head loss , → the possibility of cavitation Class quiz) The pump below delivers 0. 06 m 3/s flow of 25 o. C water and the intake pipe diameter is 20 cm. The pipe length bet. pipe inlet and pump intake is 10 ft. The pump intake is located 2 m above the water surface level in the reservoir. What is the NPSH for this system? (entrance loss coeff. =0. 1, bend loss coeff. =0. 2, f=0. 015, Ex 14. 7)

Dimensional Analysis and Similitude (차원해석과 상사) The analytical solutions directly describing fluid behavior → very limited Verification of the fluid model solutions → experiments using physical models How to perform experiments? - determine variables (parameters) - set up appropriate relationships (governing equations) for the fluid behavior using variables - set up / perform physical model as a function of variables - determine the correlations among the variables in the relationships Possibly too many experiments required depending on the complexity of geometrical fluid characteristics and the number of variables involved By reducing the number of variables via dimensional analysis, we can save our efforts, time, and cost significantly. Example, Analysis of an fluid passing an orifice, Reduction in the correlating parameters from 5 to 2

Buckingham theorem The number of independent dimensionless groups of variables (dimensionless parameters) = n – m n: the number of variables involved m: the number of basic dimensions included in the variables The dimensionless parameters – “ groups” The equation describing a physical system that has n dimensional variables Expressed in terms of dimensionless parameters ( groups)

Dimensional analysis Determination of groups 1. Identification of all independent variables describing physical phenomena (geometry, fluid characteristics, impacts on the fluid, etc. – the number of variables = n 2. Determination of basic dimensions (typically, M, L, T) – the number of basic dimensions = m 3. Expression of variables with the basic dimensions 4. Determination of groups by combining the variables to form dimensionless parameters = the number of dimensionless groups ( groups) = n - m Step-by-step method (Ipsen’s method) Elimination of basic dimensions step-by-step Always yields the correct number of parameters Exponent method Combine variables as the product Set up a set of algebraic simultaneous equations consist of the exponents of the variables (based on dimensional homogeneity) Solve the algebraic simultaneous equations – select the most frequently shown exponents as variables (repeating parameters) which will not be solved Express the relationship in a dimensionless form Remark Identification of significant variables → based on experience Double-inclusion of variables Omission of significant variables

Common groups in fluid mechanics A hypothetical flow Determination of pressure difference btw. two points, P = f(V, L, , , Ev, , ) V: velocity, L: characteristic length, : density, : viscosity, Ev : bulk modulus of elasticity, : surface tension, : specific weight → important when free-surface phenomena (waves) exist (open channel, ship model, etc. ) General form Step-by-step method (Ipsen’s method) Exponent method

Forces involved in a general flow situation Pressure force Inertial force Viscous force Compressibility force Surface (tension) force Gravity force Dimensionless numbers defined by the ratios of forces involved, Euler number (Cp) = Reynolds number = Mach number = Weber number = Froude number =

Experiment in fluid dynamics Prototype – original target structures for the fluid dynamic analysis (real-scale) Model – made for the analysis of performance of prototype via experiments, usually smaller than prototype Similitude – relationships of physical properties btw prototype and model, required for the acceptable prediction of prototype performance from model observations ¢ Model design/construction ¢ Performance test ¢ Analysis of experimental results not considered in theoretical aspects 1. Geometric similitude (기하학적 상사) – the most obvious/basic requirement in similitude, match of geometric scales (dimensions, sizes) btw prototype and model 2. Kinematic similitude (운동학적 상사) – the ratios of physical terms related to the flow (v, a, Q, etc. ) must be constant time ratio, velocity ratio, acceleration ratio, flowrate ratio,

3. Dynamic similitude (역학적 상사) – the ratios of the forces acting on corresponding masses in the model and prototype must be constant throughout the flow field similarity in flow pattern Satisfaction of similitude If couple of significant groups were equal, the dynamic (and kinematic) similitude will be met. All involved groups should NOT necessarily be equal since all forces are neither acting on nor significant (negligible, or sometimes canceled by each other) in particular fluid motions. In general, the equality of 1 or 2 significant groups satisfy the dynamic similitude

Similitude in forces represented by groups Ratio of pressure forces and inertial forces Ratio of inertial forces and viscous forces Ratio of inertial forces and compressibility forces Ratio of inertial forces and surface forces Ratio of inertial forces and gravity forces

Significance of the common groups Euler number – flows in which pressure drop is important (most flow situations; e. g. , closed conduits-no impacts on gravity, surface tension, compressibility → no need for the consideration of Fr, We, and M) Reynolds number – flows that are influenced by viscous effects: internal flows, boundary layer flows etc. (most non-ideal flow situations) Mach number – compressibility is important in these flows, usually V>0. 3 c (sound velocity) Weber number – surface tension influences the flow, flow with an interface (liquid flow facing gases or solids, bubbles, surface of orifice/weir of which head is very small, etc. ) Froude number – flows that are influenced by gravity, primarily free-surface flows in which waves are involved