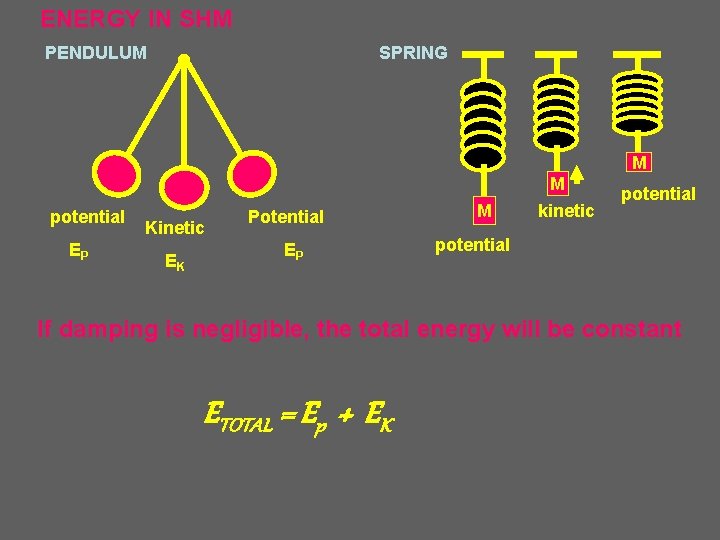
ENERGY IN SHM PENDULUM SPRING M M potential
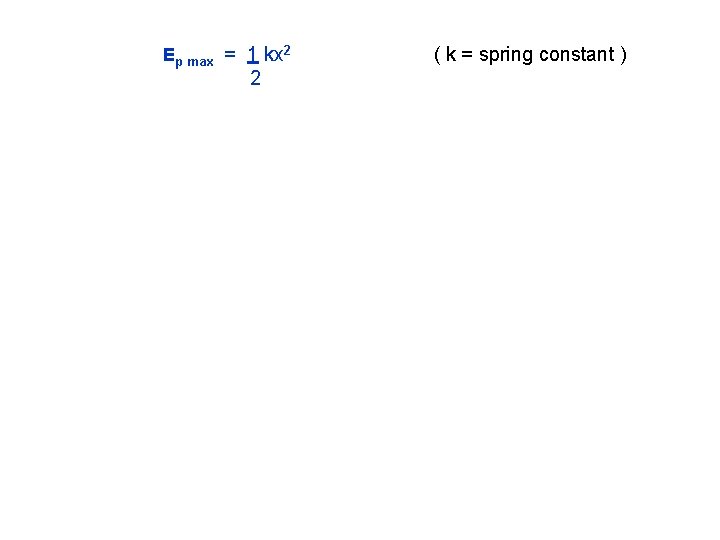














- Slides: 22

ENERGY IN SHM PENDULUM SPRING M M potential EP Kinetic EK Potential EP M kinetic potential If damping is negligible, the total energy will be constant ETOTAL = Ep + EK

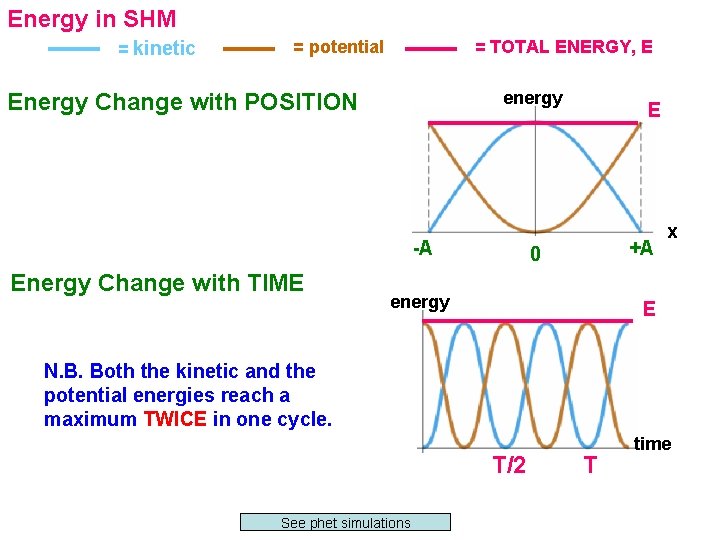
Energy in SHM = kinetic = TOTAL ENERGY, E = potential energy Energy Change with POSITION -A Energy Change with TIME E +A 0 energy x E N. B. Both the kinetic and the potential energies reach a maximum TWICE in one cycle. T/2 See phet simulations T time
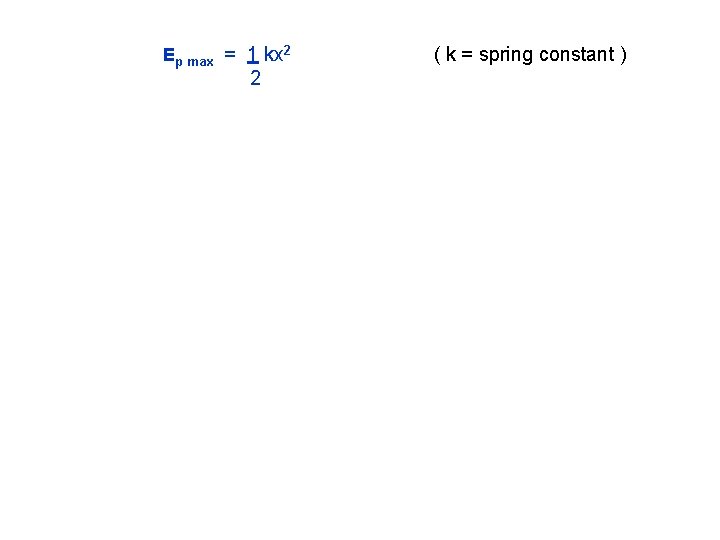
Ep max = 1 kx 2 ( k = spring constant ) 2 Hence ET = 1 kx 2 = 1 k. A 2 ( 2 2 Because ET = Ek + Ep Then Ek = ET - Ep Then Ek = 1 k. A 2 - 1 kx 2 And Ek = 1 k (A 2 - x 2) 2 2 2 (A = Amplitude) )

Ep max = 1 kx 2 ( k = spring constant ) 2 Hence ET = 1 kx 2 = 1 k. A 2 ( 2 2 Because ET = Ek + Ep Then Ek = ET - Ep Then Ek = 1 k. A 2 - 1 kx 2 And Ek = 1 k (A 2 - x 2) 2 2 2 (A = Amplitude) )

Ep max = 1 kx 2 ( k = spring constant ) 2 Hence ET = 1 kx 2 = 1 k. A 2 ( 2 2 Because ET = Ek + Ep Then Ek = ET - Ep Then Ek = 1 k. A 2 - 1 kx 2 And Ek = 1 k (A 2 - x 2) 2 2 2 (A = Amplitude) )

Ep max = 1 kx 2 ( k = spring constant ) 2 Hence ET = 1 kx 2 = 1 k. A 2 ( 2 2 Because ET = Ek + Ep Then Ek = ET - Ep Then Ek = 1 k. A 2 - 1 kx 2 And Ek = 1 k (A 2 - x 2) 2 2 2 (A = Amplitude) )

Ep max = 1 kx 2 ( k = spring constant ) 2 Hence ET = 1 kx 2 = 1 k. A 2 ( 2 2 Because ET = Ek + Ep Then Ek = ET - Ep Then Ek = 1 k. A 2 - 1 kx 2 And Ek = 1 k (A 2 - x 2) 2 2 2 (A = Amplitude) )

Ep max = 1 kx 2 ( k = spring constant ) 2 Hence ET = 1 kx 2 = 1 k. A 2 ( 2 2 Because ET = Ek + Ep Then Ek = ET - Ep Then Ek = 1 k. A 2 - 1 kx 2 And Ek = 1 k (A 2 - x 2) 2 2 2 (A = Amplitude) )

from Ek = 1 m v 2 = 2 v 2 = Since (2πf)2 = v = Vmax at x=0 = 1 k (A 2 - x 2) 2 ( v = velocity at displacement x) k (A 2 - x 2) m k m (2πf)2 (A 2 - x 2) +- (2πf) √ (A 2 (2πf) A w r !! x 2)

from Ek = 1 m v 2 = 2 v 2 = Since (2πf)2 = v = Vmax at x=0 = 1 k (A 2 - x 2) 2 ( v = velocity at displacement x) k (A 2 - x 2) m k m (2πf)2 (A 2 - x 2) +- (2πf) √ (A 2 (2πf) A w r !! x 2)

from Ek = 1 m v 2 = 2 v 2 = Since (2πf)2 = v = Vmax at x=0 = 1 k (A 2 - x 2) 2 ( v = velocity at displacement x) k (A 2 - x 2) m k m (2πf)2 (A 2 - x 2) +- (2πf) √ (A 2 (2πf) A w r !! x 2)

from Ek = 1 m v 2 = 2 v 2 = Since (2πf)2 = v = Vmax at x=0 = 1 k (A 2 - x 2) 2 ( v = velocity at displacement x) k (A 2 - x 2) m k m (2πf)2 (A 2 - x 2) +- (2πf) √ (A 2 (2πf) A w r !! x 2)

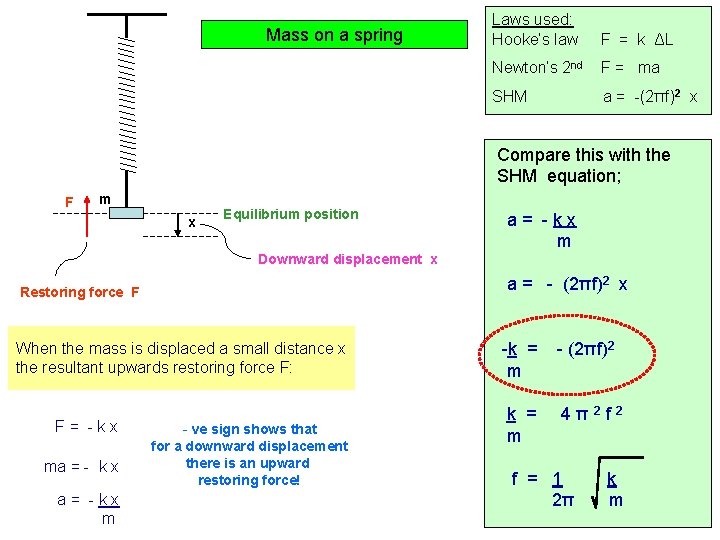
Mass on a spring Laws used: Hooke’s law F = k ΔL Newton’s 2 nd F = ma SHM a = -(2πf)2 x Compare this with the SHM equation; F m x Equilibrium position a= -kx m Downward displacement x a = - (2πf)2 x Restoring force F When the mass is displaced a small distance x the resultant upwards restoring force F: F= -kx ma = - k x a= -kx m - ve sign shows that for a downward displacement there is an upward restoring force! -k = m - (2πf)2 k = m 4π2 f 2 f = 1 2π k m

from Ek = 1 m v 2 = 2 v 2 = Since (2πf)2 = v = Vmax at x=0 = 1 k (A 2 - x 2) 2 ( v = velocity at displacement x) k (A 2 - x 2) m k m (2πf)2 (A 2 - x 2) +- (2πf) √ (A 2 (2πf) A w r !! x 2)

from Ek = 1 m v 2 = 2 v 2 = Since (2πf)2 = v = Vmax at x=0 = 1 k (A 2 - x 2) 2 ( v = velocity at displacement x) k (A 2 - x 2) m k m (2πf)2 (A 2 - x 2) +- (2πf) √ (A 2 (2πf) A w r !! x 2)

from Ek = 1 m v 2 = 2 v 2 = Since (2πf)2 = v = Vmax at x=0 = 1 k (A 2 - x 2) 2 ( v = velocity at displacement x) k (A 2 - x 2) m k m (2πf)2 (A 2 - x 2) +- (2πf) √ (A 2 (2πf) A w r !! x 2)

from Ek = 1 m v 2 = 2 v 2 = Since (2πf)2 = v = Vmax at x=0 = 1 k (A 2 - x 2) 2 ( v = velocity at displacement x) k (A 2 - x 2) m k m (2πf)2 (A 2 - x 2) +- (2πf) √ (A 2 (2πf) A w r !! x 2)

from Ek = 1 m v 2 = 2 v 2 = Since (2πf)2 = v = Vmax at x=0 = 1 k (A 2 - x 2) 2 ( v = velocity at displacement x) k (A 2 - x 2) m k m (2πf)2 (A 2 - x 2) +- (2πf) √ (A 2 (2πf) A w r !! x 2)

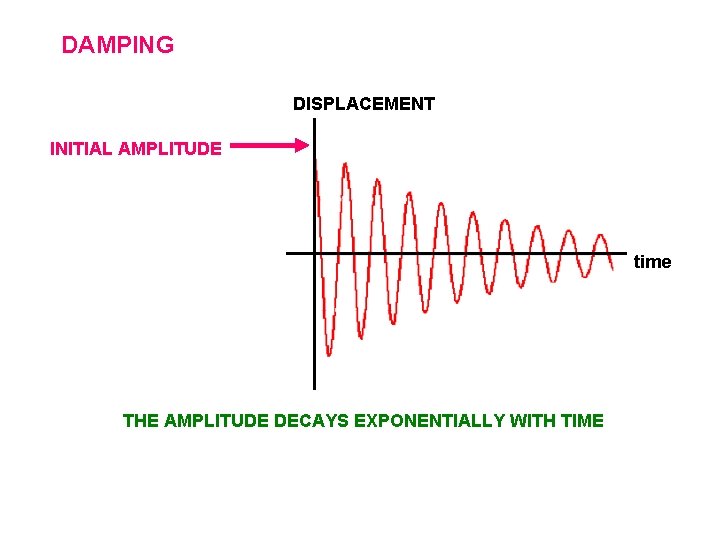
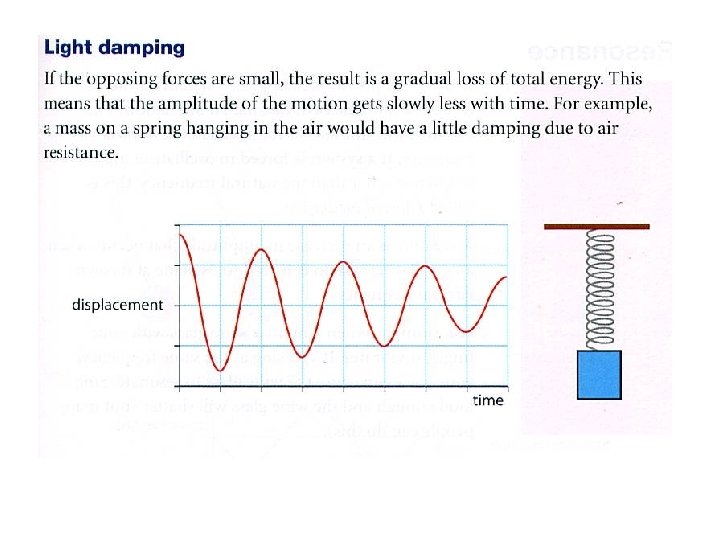
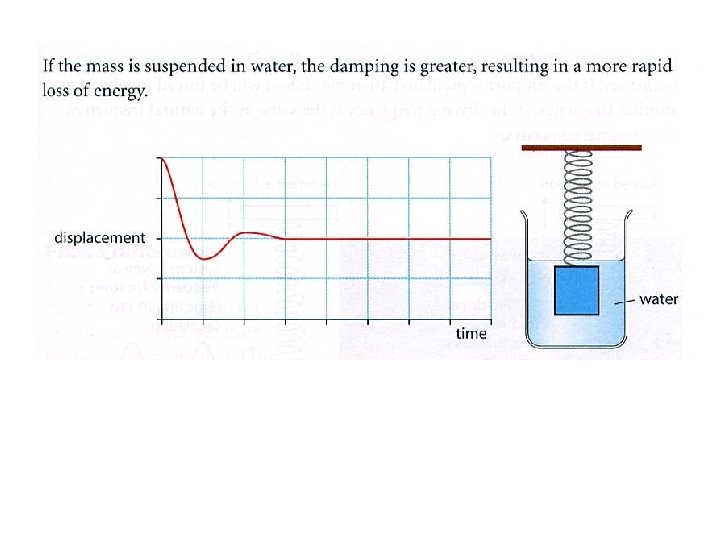
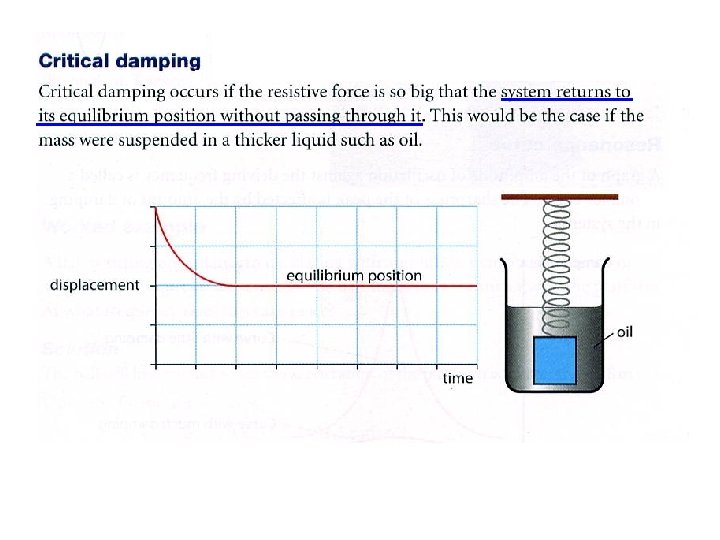
DAMPING DISPLACEMENT INITIAL AMPLITUDE time THE AMPLITUDE DECAYS EXPONENTIALLY WITH TIME


