ENERGY Energy was traditionally defined as the ability

ENERGY

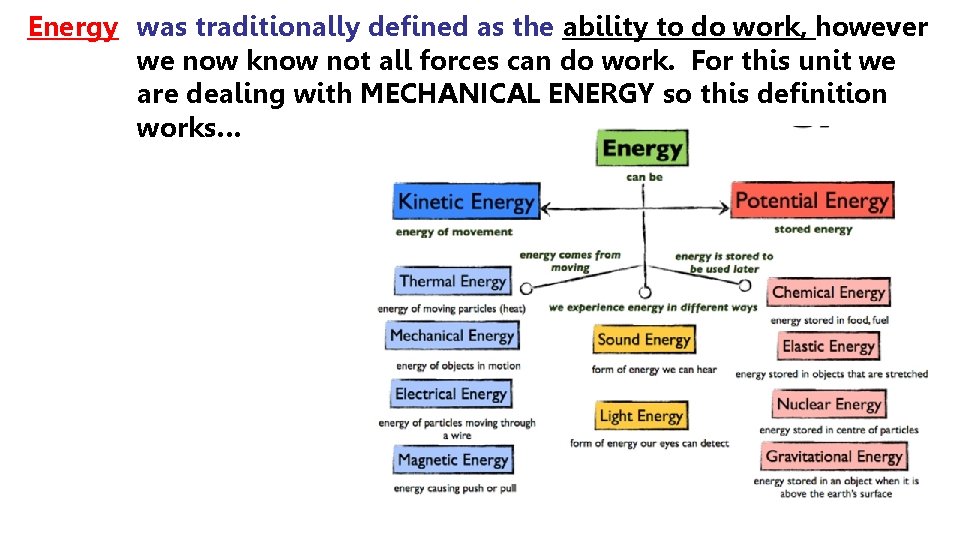
Energy was traditionally defined as the ability to do work, however we now know not all forces can do work. For this unit we are dealing with MECHANICAL ENERGY so this definition works…

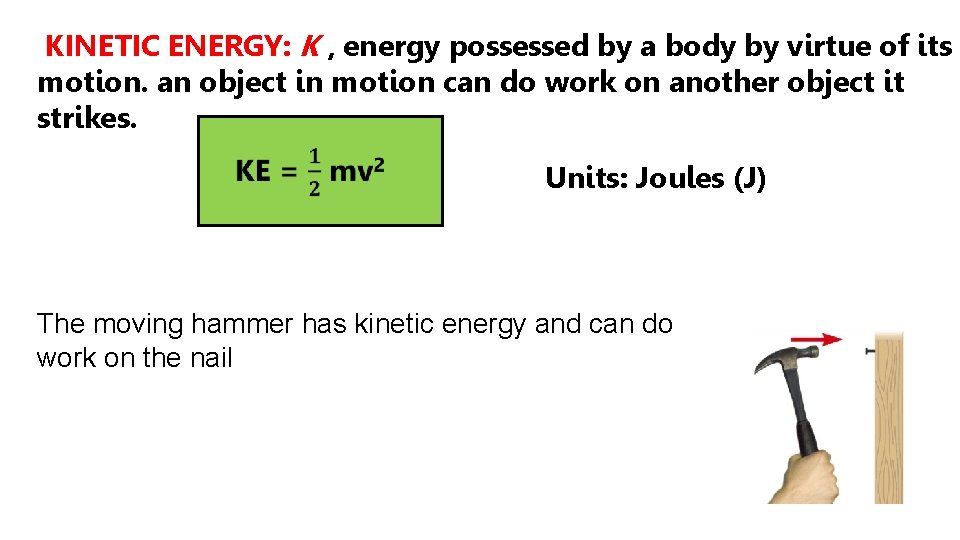
KINETIC ENERGY: K , energy possessed by a body by virtue of its motion. an object in motion can do work on another object it strikes. Units: Joules (J) The moving hammer has kinetic energy and can do work on the nail

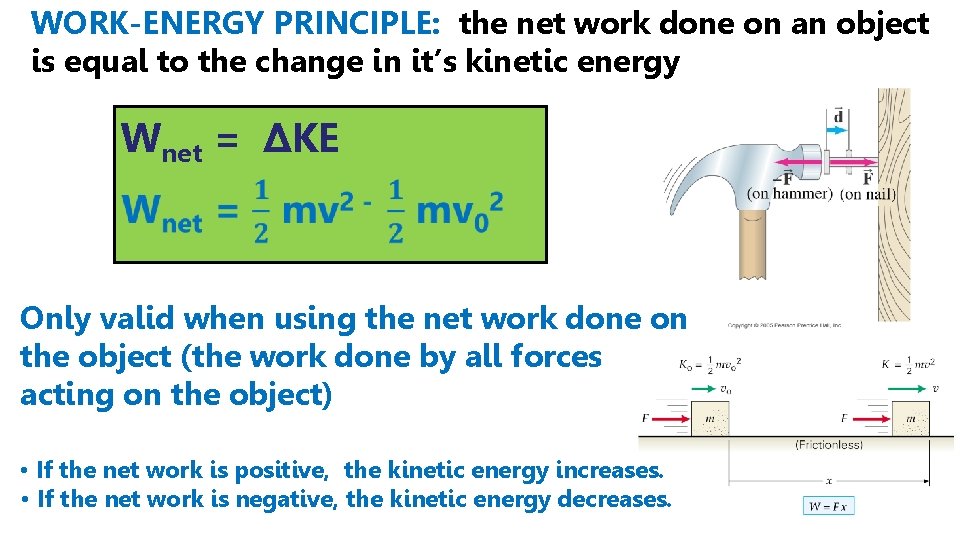
WORK-ENERGY PRINCIPLE: the net work done on an object is equal to the change in it’s kinetic energy Wnet = ΔKE Only valid when using the net work done on the object (the work done by all forces acting on the object) • If the net work is positive, the kinetic energy increases. • If the net work is negative, the kinetic energy decreases.

Deriving the equation for the WORK-ENERGY PRINCIPLE: using newton’s second law formula and the formula for work, determine the connection between work and kinetic energy Wnet = Fd mad

Ex. 8 What average force F is necessary to stop a 16 g bullet traveling at 260 m/s as it penetrates into wood at a distance of 12 cm? m= d= vo = vf = W = ΔK = ½ mv 2 - ½ mvo 2 Fd = ½ mv 2 – ½ mvo 2 F = - ½ mvo 2 d F=

Ex. 9 A 1200 kg car is traveling at 18 m/s when it applies its brakes. If the brakes allow friction to exert a 2000 N force on the car, and the brakes are applied for 50 m, how fast is the car moving when the brakes are released? W = ΔK = ½ mv 2 - ½ mvo 2 m = 1200 kg Ff = 2000 N d = 50 m vo = 18 m/s vf = ? m/s Fd = ½ mv 2 – ½ mvo 2 2000 (50) = ½ 1200 v 2 - ½ 1200 • 18 2

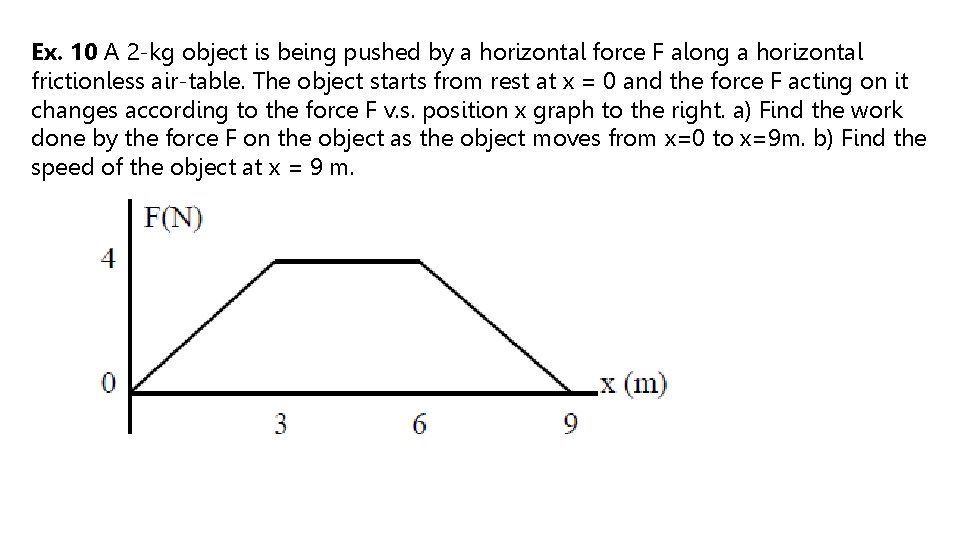
Ex. 10 A 2 -kg object is being pushed by a horizontal force F along a horizontal frictionless air-table. The object starts from rest at x = 0 and the force F acting on it changes according to the force F v. s. position x graph to the right. a) Find the work done by the force F on the object as the object moves from x=0 to x=9 m. b) Find the speed of the object at x = 9 m.

POTENTIAL ENERGY: U, Energy associated with forces that depend on an object’s position. Potential energy is a property of the system, not of the object A system is a collection of objects interacting via forces or processes that are internal to the system Familiar examples of potential energy: • A wound-up spring • A stretched elastic band • An object at some height above the ground

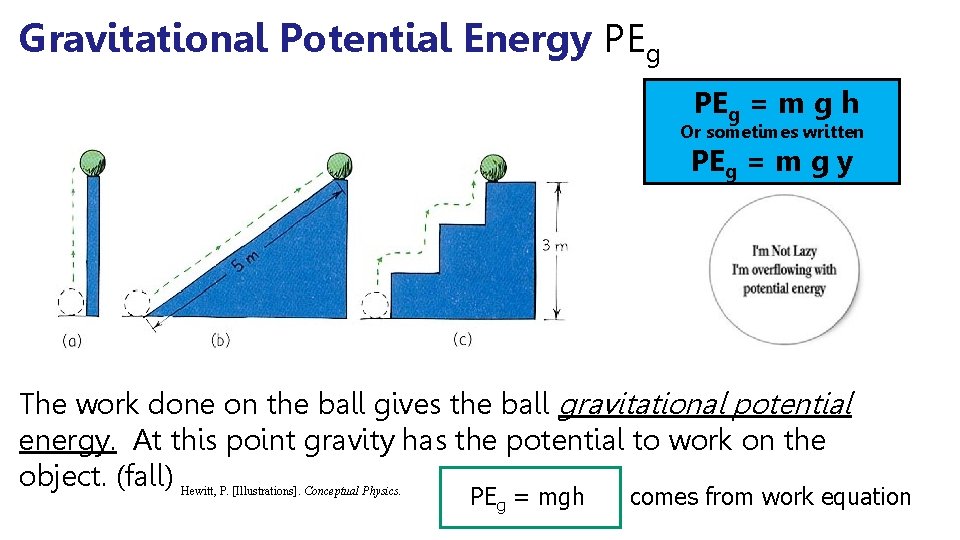
Gravitational Potential Energy PEg = m g h Or sometimes written PEg = m g y The work done on the ball gives the ball gravitational potential energy. At this point gravity has the potential to work on the object. (fall) Hewitt, P. [Illustrations]. Conceptual Physics. PEg = mgh comes from work equation

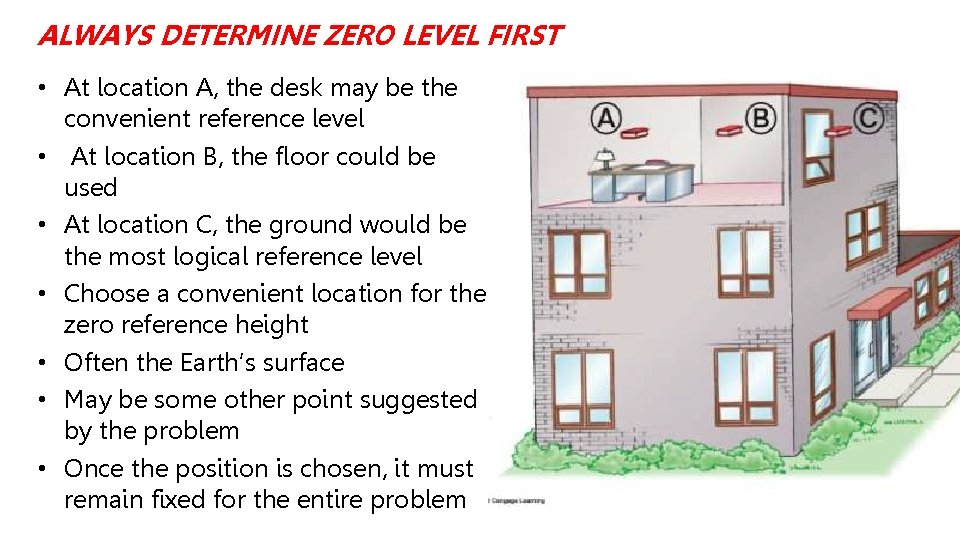
ALWAYS DETERMINE ZERO LEVEL FIRST • At location A, the desk may be the convenient reference level • At location B, the floor could be used • At location C, the ground would be the most logical reference level • Choose a convenient location for the zero reference height • Often the Earth’s surface • May be some other point suggested by the problem • Once the position is chosen, it must remain fixed for the entire problem

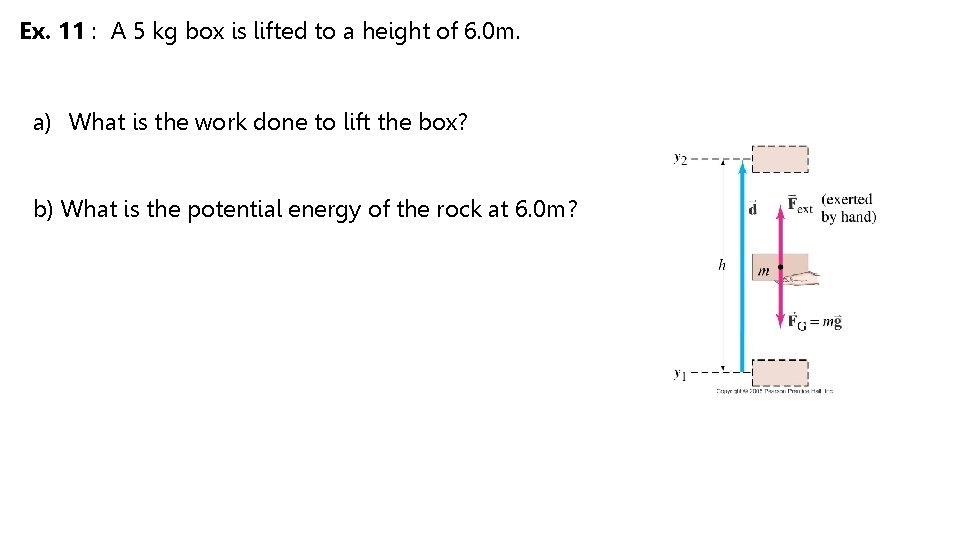
Ex. 11 : A 5 kg box is lifted to a height of 6. 0 m. a) What is the work done to lift the box? b) What is the potential energy of the rock at 6. 0 m?

Elastic Potential Energy PEs Potential energy can also be stored in a spring when it is compressed; the figure below shows potential energy yielding kinetic energy. Formulas The force required to compress or stretch a spring is: Fs =- kx or Fs = kx k is called the spring constant, and needs to be measured for each spring. x is the distance from equilibrium of the stretch or compression of the spring

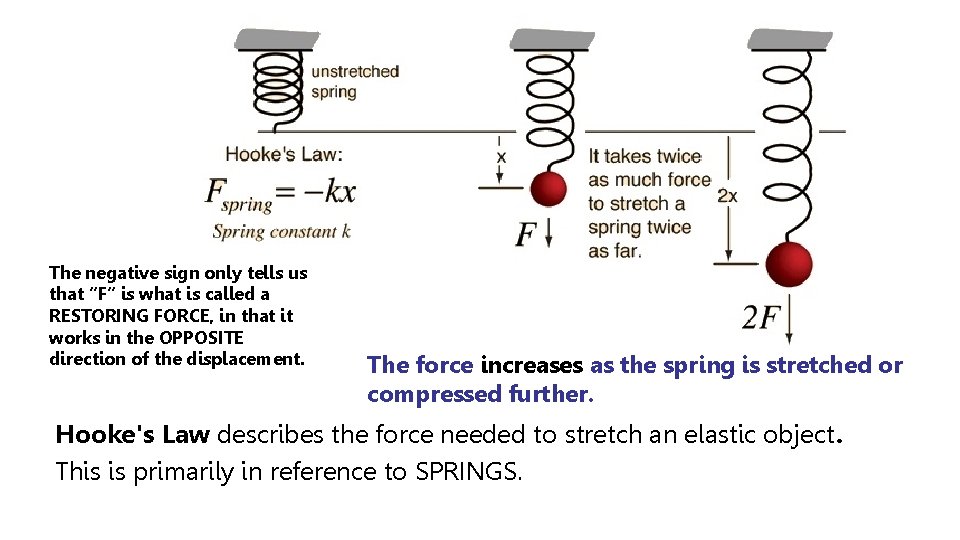
The negative sign only tells us that “F” is what is called a RESTORING FORCE, in that it works in the OPPOSITE direction of the displacement. The force increases as the spring is stretched or compressed further. Hooke's Law describes the force needed to stretch an elastic object. This is primarily in reference to SPRINGS.

A B

Ex. 12 A load of 50 N attached to a spring hanging vertically stretches the spring 5. 0 cm. The spring is now placed horizontally on a table and stretched 11. 0 cm. What force is required to stretch the spring this amount? 1000 N/m 110 N

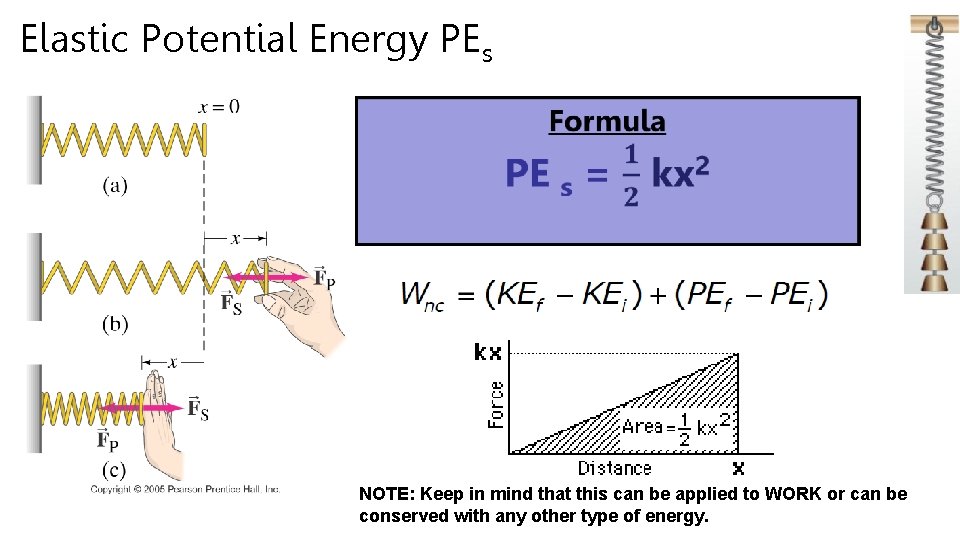
Elastic Potential Energy PEs NOTE: Keep in mind that this can be applied to WORK or can be conserved with any other type of energy.

CONSERVATIVE VS NON CONSERVATIVE FORCES CONSERVATIVE WORK DONE DOES NOT DEPEND ON THE PATH TAKEN GRAVITATIONAL PE ELASTIC PE ELECTRIC PE Potential energy can only be defined for conservative forces. NON CONSERVATIVE WORK DOES DEPEND ON THE PATH TAKEN PUSH OR PULL BY A PERSON FRICTION AIR RESISTANCE TENSION ROCKET /MOTOR These forces are generally dissipative and work done against it cannot easily be recovered

CONSERVATIVE The work done by a conservative force depends only on the initial and final position of the object acted upon. An example of a conservative force is gravity. The work done equals the change in potential energy and depends only on the initial and final positions above the ground and NOT on the path taken. In a conservative system: Ei=Ef

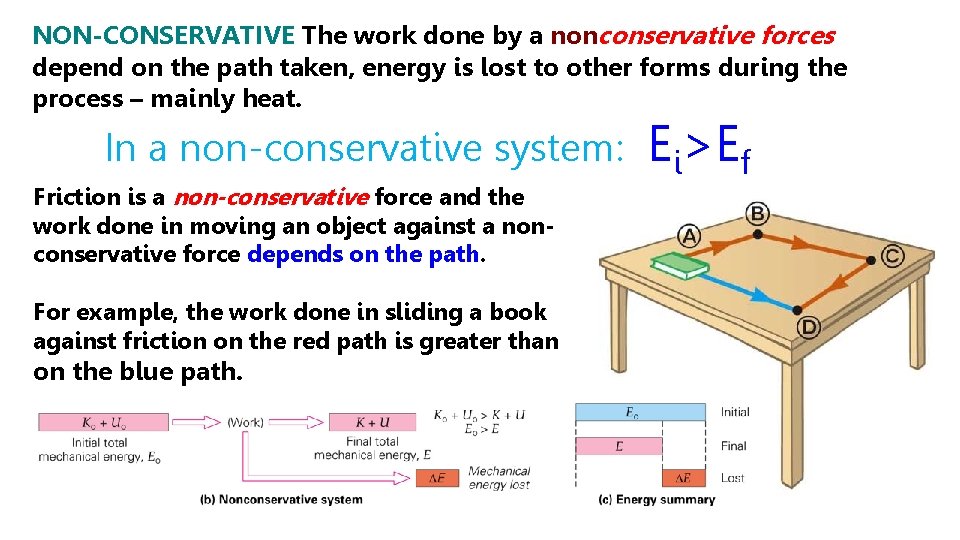
NON-CONSERVATIVE The work done by a nonconservative forces depend on the path taken, energy is lost to other forms during the process – mainly heat. In a non-conservative system: Friction is a non-conservative force and the work done in moving an object against a nonconservative force depends on the path. For example, the work done in sliding a book against friction on the red path is greater than on the blue path. Ei>Ef

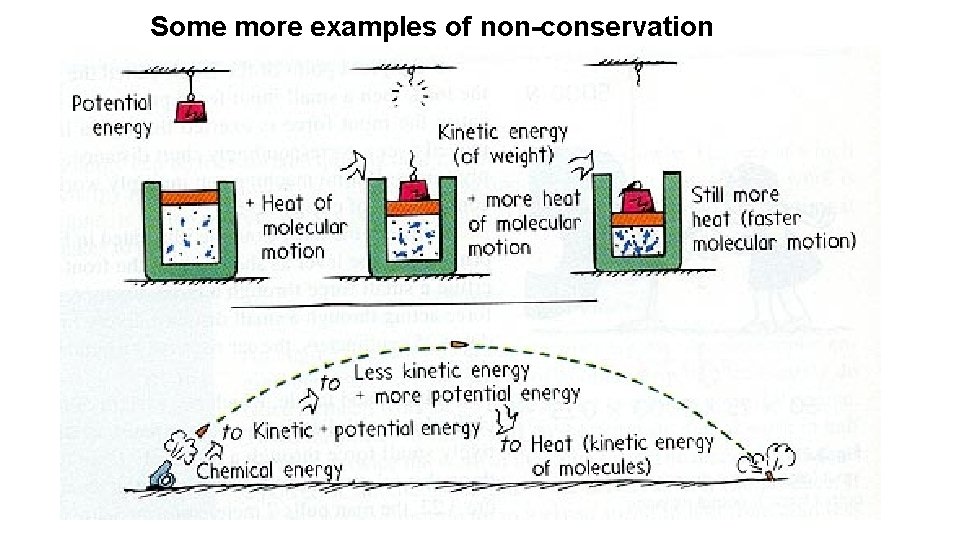
Some more examples of non-conservation