Energy economics 1 Key components of energy economics

Energy economics 1

Key components of energy economics Basic economic principles Cost elements of energy technology Investment analysis Financial matrices and tools Life cycle costs and savings

Economic-evaluation methods can be used in a number of ways to increase the economic efficiency of energy-related decisions. • To obtain the largest possible energy savings. – As an example, a plant owner may budget a specific sum of money for the purpose of retrofitting the plant for energy efficiency. • To achieve a targeted reduction in energy for the lowest possible efficiency/renewable energy investment; – As an example, designers may be required by state or federal building standards and/or codes to reduce the design energy loads of new buildings below some specified level. 3

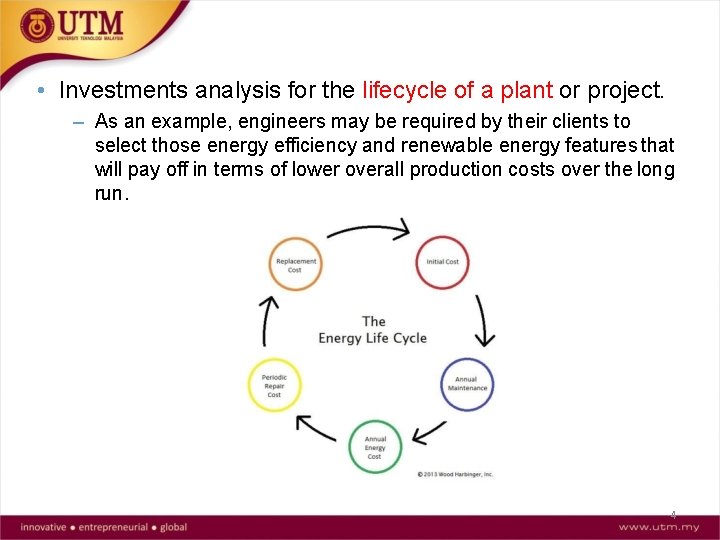
• Investments analysis for the lifecycle of a plant or project. – As an example, engineers may be required by their clients to select those energy efficiency and renewable energy features that will pay off in terms of lower overall production costs over the long run. 4

Economic efficiency • Economic efficiency is not necessarily the same as engineering thermal efficiency. • For example, one furnace may be more “efficient” than another in the engineering technical sense, if it delivers more units of heat for a given quantity of fuel than another. Yet it may not be economically efficient if the initial cost of the higher-output furnace outweighs its fuel savings. Engineering. Efficiency Economicefficiency Energyoutput Fuelinput Energyoutput Investment 5

Economic components • The economics of energy systems includes the initial cost of delivering components (turbines, high-voltage transmission lines, air-conditioner, pump, compressor and so forth); • Ongoing costs associated with fuel, maintenance, wages, rental, and other costs; • Energy economics is itself a highly specialized and elaborate field with a very large body of knowledge in support. • An engineer needs basic knowledge of the interface between energy technology and energy economics 6

• Capital cost: Capital cost is the initial cost incurred on the project, it includes cost of system, wiring, civil work, commission charges, cost of land, etc. • Initial cost: A one-time expense incurred at the beginning of the first compounding period, for example, to purchase some major asset for an energy system. • Debt: Debt financing is the loaning of money from one party to another with the expectation that the receiving party will pay back the amount loaned along with an interest. • Equity: Equity is the provision of money in return for partial ownership of the project. 7

• Operation and maintenance cost: is the annual recurring cost required to carry on the functioning of the plant from day to day basis. • Fuel cost: The cost involved in purchase of the fuel, usually zero in the Renewable energy projects. • Grant/capital subsidy/ rebate: Grant or capital subsidy is a provision of money to the investors without expectations of any type of return from them. • Return on investment (ROI): Return on investment (ROI) is the benefit to an investor resulting from an investment of some resource. 8

• Repayment period: It refers to the amount of time before full repayment. • Grace period: The grace period is the initial period during which borrowers do not repay loan. • Interest rates or discount rates: A rate is an agreement between borrower and lender, which is charged or paid for the use of money. 9

• Annual escalation rate: Escalation is the increase in the costs/revenues per year. • Periodic replacement cost: In case of Solar PV and wind based project, batteries need to be replaced by a certain time period. • Depreciation: Depreciation is non-cash expense to account the reduction in the value of an asset as a result of wear and tear, age, or obsolescence. 10

• Term of project: Planning horizon over which the cash flow of a project is to be assessed, N. • Annuity: An annuity is a series of payments made at equal intervals. Annuities can either be positive (e. g. , annual revenues from the sales of energy from a project) or negative (e. g. , annual expenditure on maintenance). • Salvage value: A one-time positive cash flow at the end of the planning horizon of a project due to sale of the asset, system, and the like, in its actual condition at the end of the project. 11

• Money returned in the future is not worth as much as money invested today. • The change in value of money over time is given the name time value of money. 12

Equations for Present, Annual, and Future Values • Given interest rate i, time horizon of N years, and a present value P, the future value of that amount F is given by DF 1 ( 1 i) N Here DF is called discount factor • If you borrow today an amount P, you have to refund an amount A (i. e. annuities) over a period of N years i(1 i ) N AF N ( 1 i) 1 • Here AF is called annuity factor 13

• The future value F of the annuity at the end of the Nth year can be calculated as • These formulas can be inverted when needed, for example, if one knows F and wishes to calculate P, then can be rewritten P = F/(1 + i)N, and so on. 14

• Example 3 -2 A cash flow stream consists of an annuity of $100, 000 earned for 10 years at 7% interest. What is the future value of this stream at the end of term? What is the value of the factor (F/A, i%, N) in this case? • Then (F/A, 7%, 10) = $1, 381, 645/$100, 000 = 13. 82. 15

1. The present worth method is one approach where all elements of the financial analysis of the project are discounted back to their present worth. 2. The annual worth method is where discounting all cost components to their equivalent annual value, summing up positive and negative components. – When evaluating financial viability using the time value of money, we incorporate the chosen MARR for the project. MARR is the minimum rate required for returns from a project in order for it to be financially attractive, which is set by the business, government agency, or other entity that is making a decision about the investment. 16

• The net present value (NPV) method finds the excess of benefits over costs, where all amounts are discounted for their time value. • The NPV method is also often called the net present worth or net savings method. • Following is a formula for finding the NPV from an investment • NPV (NB) method is also useful for deciding whether to make a given investment and for designing and sizing systems. C NPV �n N n 0 Cn (1 i)n = Net cash inflow in year n 17

Internal Rate-of-Return Method (IRR) • The internal rate-of-return (IRR) method solves for the discount rate for which dollar savings are just equal to dollar costs over the entire period; • The rate for which the NPV is zero. • This discount rate is the rate of return on the investment. • It is compared to the investor’s minimum acceptable rate of return to determine whether the investment is desirable. NPV Cn n 0 (1 i) N n i IRR : NPV 0

• Example 3 -3 A municipality is considering an investment in a small-scale energy system that will cost $6. 5 million to install, and then generate a net annuity of $400, 000/year for 25 years, with a salvage value at the end of $1 million. (a) Calculate the net worth of the project using simple payback. (b) Suppose they set the MARR at 5%, what is the net present worth of the project by this approach? 19

• Example 3 -4 : A municipality is considering an investment in a small-scale energy system that will cost $6. 5 million to install, and then generate a net annuity of $400, 000/year for 25 years, with a salvage value at the end of $1 million. (a) Calculate the IRR for the investment 20

• A third approach is to calculate the benefit-cost ratio, or ratio of all the benefits of the project to all of the costs. • For instance, a project to build a hydroelectric dam might provide benefits in the form of boating, fishing, and water for irrigation. The benefit of each could be estimated and included in the sum of benefits in the ratio. • In general, if the B/C ratio is greater than 1, the project is acceptable, and if it is less than 1, it is not. • Where the B/C ratio is close to 1, the decision-maker should re-examine the inputs to make sure they are as accurate as possible, and to look for any additional information that might help to make a decision one way or the other. B/C NPV C C 21

• Example 3 -5 Calculate the B/C ratio for the investment in Example 3 -3, (a) using the present worth of all costs and benefits, and (b) using the annual worth of all costs and benefits. 22

• Example 3 -6 Now suppose the project of Example 3 -3 includes an annual operating cost of $50, 000, with all other values remaining the same. Calculate B/C ratios using the present worth of all benefits and costs. 23

Advantages and Disadvantages of NPV, IRR, and B/C Methods • Advantages: • With the NPV method, the advantage is that it is a direct measure of the dollar contribution to the stockholders. • With the IRR method, the advantage is that it shows the return on the original money invested. • Disadvantages: • NPV needs cost of capital • With the IRR method, the disadvantage is that, at times, it can give you conflicting answers when compared to NPV for mutually exclusive projects. 24

• Example 3 -7 An oil company is considering adding a well to a field for the cost of $6 million. The result of this investment will be a net increase in oil production by $4. 5 million in Year 1, with the net change in production declining by $1 million for each year thereafter until the end of the investment lifetime in Year 9: Year 2 = $3. 5 M, Year 3 = $2. 5 M, and so on. Note that from Year 6 onward the change in production becomes negative, i. e. , Year 6 = −$0. 5 M, etc. , and that there is a net increase in total face value of production by $4. 5 million thanks to the new well. Show that the IRR method returns two values of i for which NPV = 0. 25

Levelized Cost of Energy (LCOE) • The LCOE is the average cost of producing per k. Wh of useful energy over the entire life cycle of the project. It includes all the costs associated with an investment and takes into account the time value of money. • The LCOE is the value that must be received for each unit of energy to ensure that all costs and a reasonable profit are made. 26

Levelized Cost of Energy Profit is ensured by discounting future revenues at a discount rate that equals the rate of return that might be gained on other investments of comparable risk, i. e. , the opportunity cost of capital. In equation form, this is represented as: LCOE Ca CO&M , a Pa Ea 27

• Example 3 -8 An electric plant that produces 2 billion k. Wh/year has an initial capital cost of $500 million and an expected lifetime of 20 years, with no remaining salvage value. The capital cost of the plant is repaid at 7% interest. Total operating cost at the plant is $25 million/year, and annual return to investors is estimated at 10% of the operating cost plus capital repayment cost. What is the levelized cost of electricity, in $/k. Wh? 28

• Example 3 -9 Recalculate NPV in Example 3 -3 using the following adjustments to reflect government support programs for the project: 1. A rebate of $200/rated k. W, if the system is rated at 5000 k. W. 2. An operating credit of $0. 025/k. Wh, if the system produces on average 1. 8 million k. Wh/year. 3. An interest rate buy-down such that the MARR for the project is reduced to 3%. 29

Risk Assessment • Risk assessment provides decision makers with information about the “risk exposure” inherent in a given decision, i. e. , the probability that the outcome will be different from the “best-guess” estimate. • Risk assessment is also concerned with the risk attitude of the decision maker that describes his/her willingness to take a chance on an investment of uncertain outcome. Risk assessment techniques are typically used in conjunction with the evaluation methods outlined earlier; and not as stand-alone evaluation techniques. • Though none takes the risk out of making decisions, the techniques—if used correctly—can help the decision maker make more informed choices in the face of uncertainty.

Exercise 1. A power plant operator is considering an investment in increased efficiency of their plant that costs $1. 2 million and lasts for 10 years, during which time it will save $250, 000/year. The investment has no salvage value. The plant has an MARR of 13%. Is the investment viable? Exercise 2. A municipality is considering an investment in a small renewable energy power plant with the following parameters. The cost is $360, 000, and the output averages 50 k. W year-round. The price paid for electricity at the plant gate is $0. 039/k. Wh. The investment is to be evaluated over a 25 -year time horizon, and the expected salvage value at the end of the project is $20, 000. The MARR is 6%. Calculate the NPV of this investment. Is it financially attractive? Calculate the operating credit per k. Wh which the government would need to give to the investment in order to make it break even financially. Express your answer to the nearest 1/1000 th of dollars. Exercise 3. An electric utility investment has a capital cost of $60 million, a term of 8 years, and an annuity of $16 million. What is the CRF for this investment? 31

Exercise 5. An interest buy down program offers to reduce interest rates by 4% from the base rate. Suppose the base rate for a loan of $8000 is 8% for 10 years. What is the monthly payment before and after the buy down? In this case, use monthly compounding, that is, the term is 120 payment periods, and the interest per month is 0. 667% before and 0. 333% after the buy down. 32

• Two options are being considered for a new cool-room. Option A involves an initial installed cost of EUR 7, 000 and an annual running cost of EUR 2, 000. Option B involves an initial installed cost of EUR 12, 000 and an annual running cost of EUR 1, 500. Calculate the Net Present Cost of these two options over the expected equipment life of ten years. Use a discount rate of 10% and ignore any inflation effects. Which of the two options would you recommend and why? What will happen to these net present costs if a higher discount rate is used? What will happen to the difference between the two net present costs? i(1 i ) N A C N 1 ( 1 i)