ENE 428 Microwave Engineering Lecture 12 Power Dividers

ENE 428 Microwave Engineering Lecture 12 Power Dividers and Directional Couplers 1

Power dividers and directional couplers § Passive components that are used for power division or combining. § The coupler may be a three-port or a four-port component § Three-port networks take the form of T-junctions § Four-port networks take the form of directional couplers and hybrids. § Hybrid junctions have equal power division and either 90 or a 180 phase shift between the outports. 2

Types of power dividers and directional couplers § T-junction power divider § Resistive divider § Wilkinson power divider § Bethe Hole Coupler § Quadrature (90 ) hybrid and magic-T (180 ) hybrid § Coupled line directional coupler 3

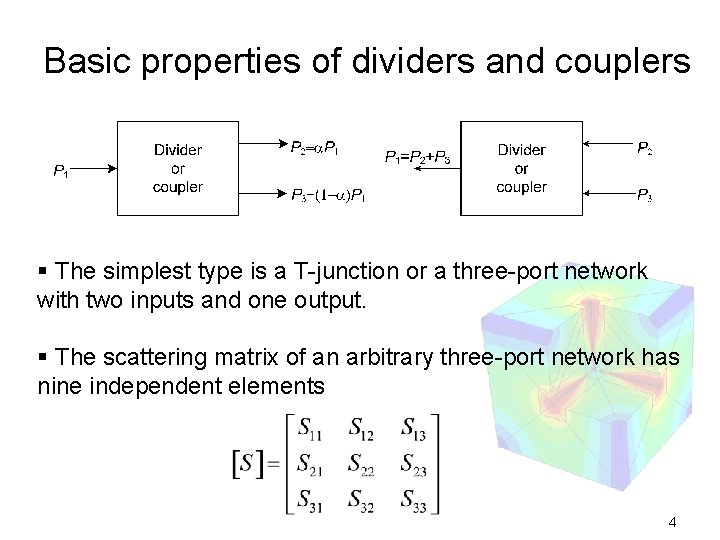
Basic properties of dividers and couplers § The simplest type is a T-junction or a three-port network with two inputs and one output. § The scattering matrix of an arbitrary three-port network has nine independent elements 4

The scattering parameters’ lossless property § The unitary matrix: § This can be written in summation form as where ij = 1 if i = j and ij = 0 if i j thus if i = j, while if i j , 5

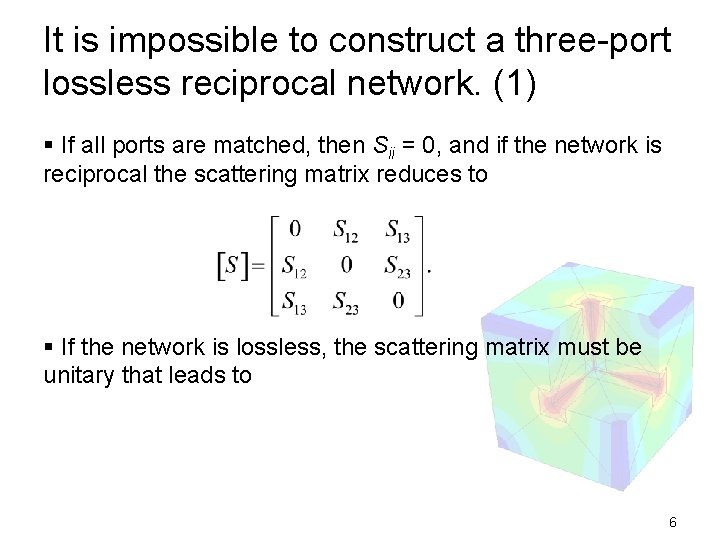
It is impossible to construct a three-port lossless reciprocal network. (1) § If all ports are matched, then Sii = 0, and if the network is reciprocal the scattering matrix reduces to § If the network is lossless, the scattering matrix must be unitary that leads to 6

It is impossible to construct a three-port lossless reciprocal network. (2) § Two of the three parameters (S 12, S 13, S 23) must be zeros but this will be inconsistent with one of eq. (1 a-c), implying that a three-port network cannot be lossless, reciprocal, and matched at all ports. 7

Any matched lossless three-port network must be nonreciprocal. (1) § The [S] matrix of a matched three-port network has the following form: § If the network is lossless, [S] must be unitary, which implies the following: 8

Any matched lossless three-port network must be nonreciprocal. (2) § Either of these followings can satisfy above equations, or 9

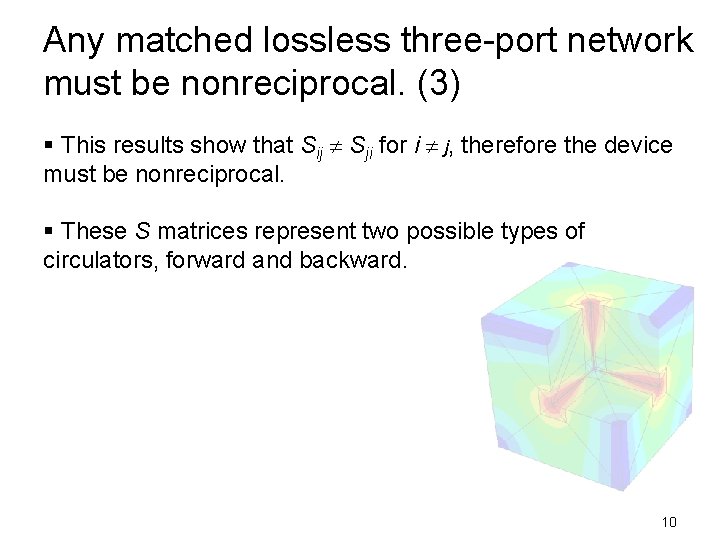
Any matched lossless three-port network must be nonreciprocal. (3) § This results show that Sij Sji for i j, therefore the device must be nonreciprocal. § These S matrices represent two possible types of circulators, forward and backward. 10

A lossless and reciprocal three-port network can be physically realized if only two of its ports are matched. (1) § If ports 1 and 2 are matched ports, then § To be lossless, the following unitary conditions must be satisfied: 11

A lossless and reciprocal three-port network can be physically realized if only two of its ports are matched. (2) § From (3 a-b), Then |S 12|=|S 33|=1. , so (3 d) shows that S 13 = S 23 = 0. 12

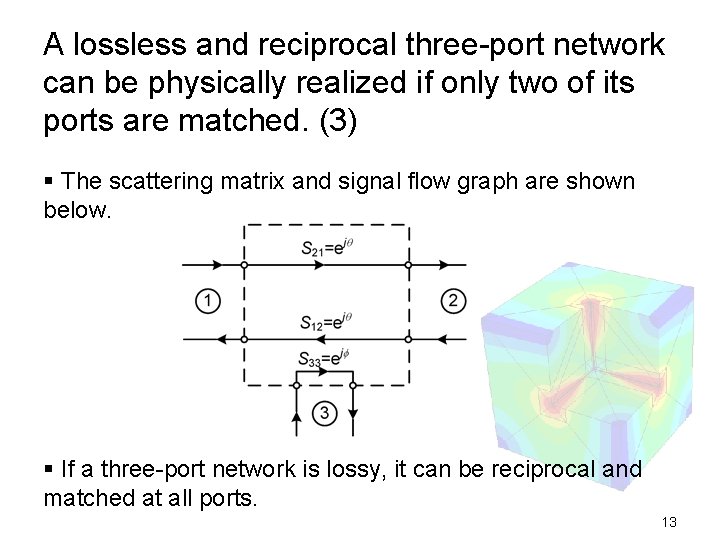
A lossless and reciprocal three-port network can be physically realized if only two of its ports are matched. (3) § The scattering matrix and signal flow graph are shown below. § If a three-port network is lossy, it can be reciprocal and matched at all ports. 13

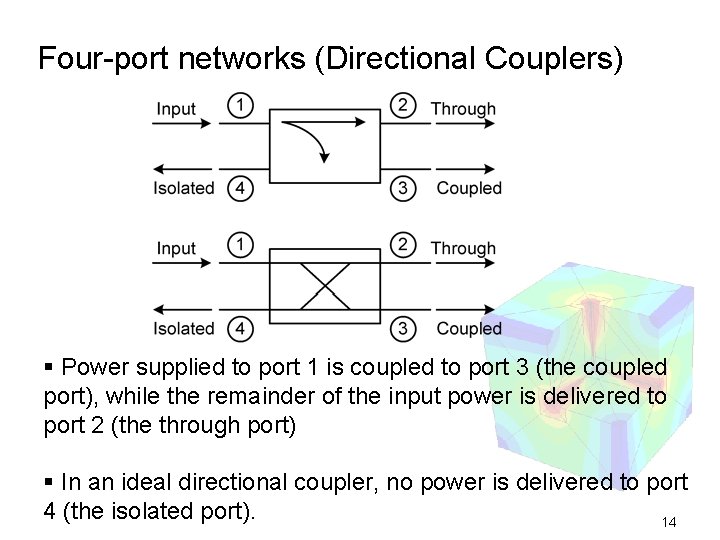
Four-port networks (Directional Couplers) § Power supplied to port 1 is coupled to port 3 (the coupled port), while the remainder of the input power is delivered to port 2 (the through port) § In an ideal directional coupler, no power is delivered to port 4 (the isolated port). 14

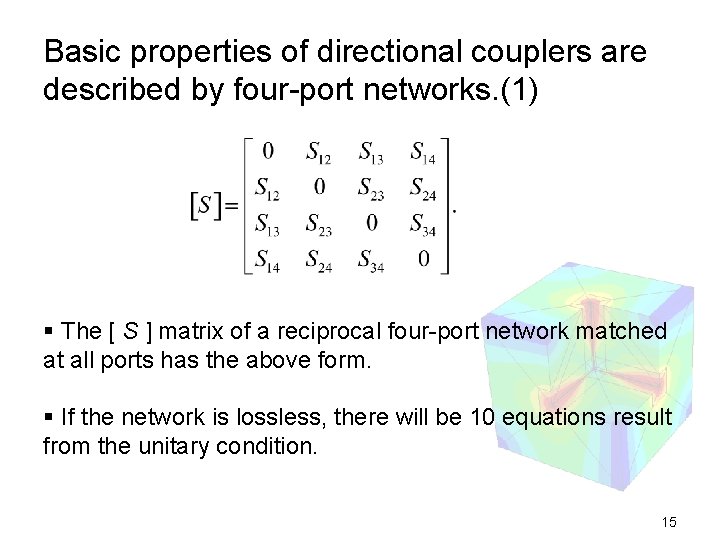
Basic properties of directional couplers are described by four-port networks. (1) § The [ S ] matrix of a reciprocal four-port network matched at all ports has the above form. § If the network is lossless, there will be 10 equations result from the unitary condition. 15

Conditions needed for a lossless reciprocal four-port network (1) § The multiplication of row 1 and row 2, and the multiplication of row 4 and row 3 can be arranged so that (4) § The multiplication of row 1 and row 3, and the multiplication of row 2 and row 4 can be arranged so that (5) § If S 14 = S 23 = 0, a directional coupler can be obtained. 16

Conditions needed for a lossless reciprocal four-port network (2) § Then the self-products of the rows of the unitary [S] matrix yield the following equations: which imply that |S 13|=|S 24|and that |S 12|=|S 24|. 17

Symmetrical and Antisymmetrical coupler (1) § The phase references of three of the four ports are chosen as S 12 = S 34 = , S 13 = ej , and S 24 = ej , where and are real, and are phase constants to be determined. § The dot products or rows 2 and 3 gives which yields a relation between the remaining phase constant as + = 2 n. 18

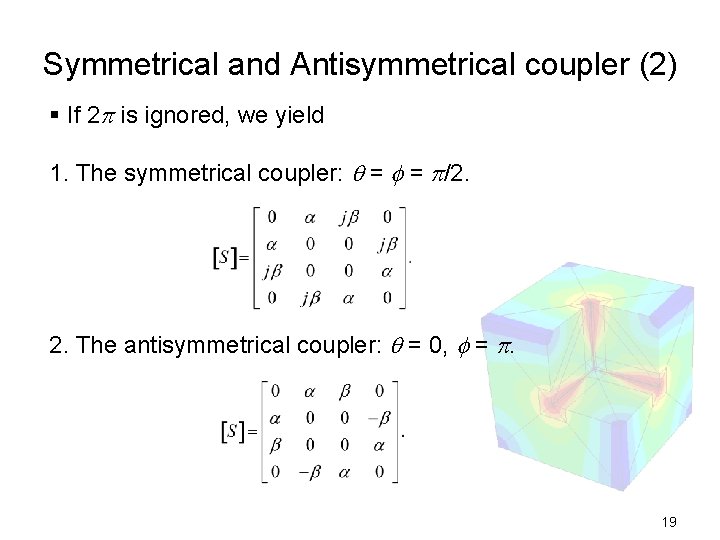
Symmetrical and Antisymmetrical coupler (2) § If 2 is ignored, we yield 1. The symmetrical coupler: = = /2. 2. The antisymmetrical coupler: = 0, = . 19

Symmetrical and Antisymmetrical coupler (3) § The two couplers differ only in the choice of the reference planes. The amplitudes and are not independent, eq (6 a) requires that 2 + 2 =1. § Another way for eq. (4) and (5) to be satisfied is if |S 13|=|S 24| and |S 12|=|S 34|. § If phase references are chosen such that S 13=S 24= and S 12=S 34=j , two possible solutions are given. First S 14=S 23=0, same as above. § The other solution is for = =0, which implies S 12=S 13=S 24=S 34=0, the case of two decoupled two-port network. 20

Directional coupler’s characterization (1) § Power supplied to port 1 is coupled to port 3 (the coupled port) with the coupling factor § The remainder of the input power is delivered to port 2 (the through port) with the coefficient § In an ideal coupler, no power is delivered to port 4 (the isolated port). § Hybrid couplers have the coupling factor of 3 d. B or = = The quadrature hybrid coupler has a 90 phase shift between ports 2 and 3 ( = = /2) when fed at port 1. 21

Directional coupler’s characterization (2) Coupling = C = Directivity = D = Isolation = I = = -20 log d. B, = 20 log d. B, = -20 log|S 14| d. B. § The coupling factor indicates the fraction of the input power coupled to the output port. § The directivity is a measure of the coupler’s ability to isolate forward and backward waves, as is the isolation. These quantities can be related as I = D + C d. B. 22

Ideal coupler § The ideal coupler would have infinite directivity and isolation (S 14 = 0). 23

The T-junction power divider § The T-junction power divider can be implemented in any type of transmission line medium. 24

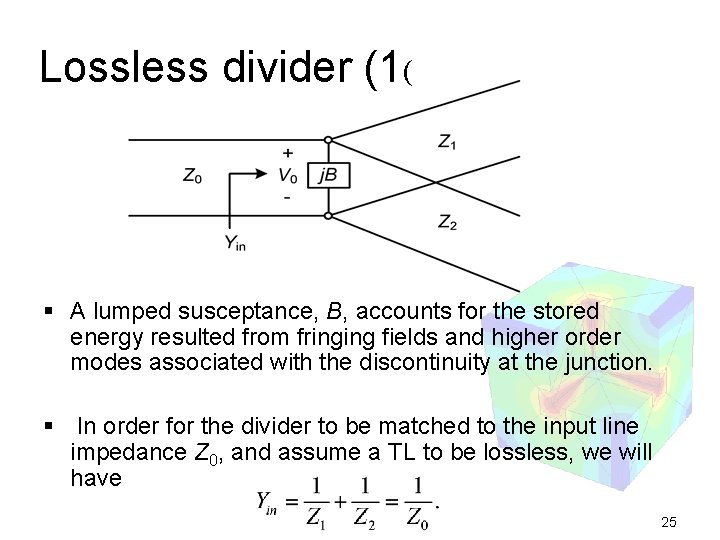
Lossless divider (1( § A lumped susceptance, B, accounts for the stored energy resulted from fringing fields and higher order modes associated with the discontinuity at the junction. § In order for the divider to be matched to the input line impedance Z 0, and assume a TL to be lossless, we will have 25

Lossless divider (2( § The output line impedances Z 1 and Z 2 can then be selected to provide various power division ratios. § In order for the divider to be matched to the input line impedance Z 0, and assume a TL to be lossless, we will have 26

Ex 1 A lossless T-junction power divider has a source impedance of 50 . Find the output characteristic impedances so that the input power is divided in a 3: 1 ratio. Compute the reflection coefficients seen looking into the output ports. 27

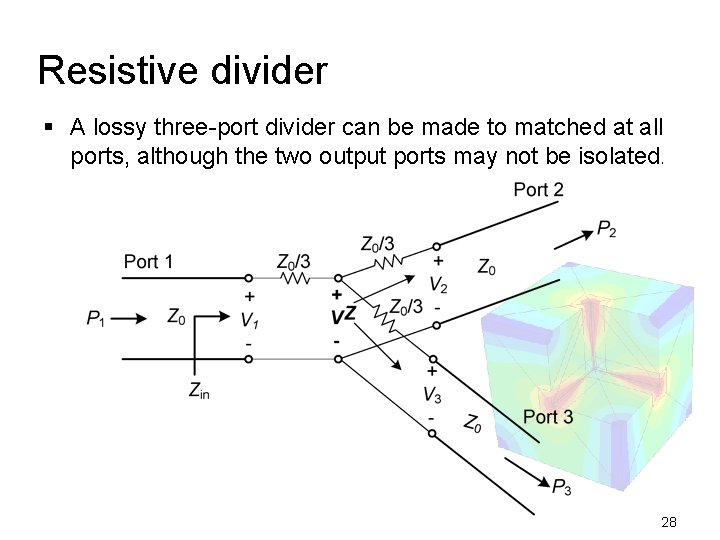
Resistive divider § A lossy three-port divider can be made to matched at all ports, although the two output ports may not be isolated. 28

The Wilkinson power divider § The lossless T-junction divider cannot be matched at all ports and does not have any isolation between output ports. § The resistive divider can be matched at all ports but the isolation is still not achieved. § The Wilkinson power divider can be matched at all ports and isolation can be achieved between the output ports. 29