End of Chapter 4 Movement of a Flood

Monoclinal Wave Velocity: Celerity • Suppose there is a big storm upstream, or a

• • Divide the cross-section in two. The flow rate of the advancing

Manning’s Equation • The average velocity V in an open channel is given by

Manning’s for a wide rectangular channel • Here wetted perimeter P is mostly B,

Celerity • If we differentiate the flow form of Manning’s we can evaluate the

Steady Flow • Now, lets jump to Chapter 7 and continue our use of

Normal Depth • Uniform flow problems use Manning’s to compute Normal depth yn, the

Overland Flow Manning’s n Roughness coefficients for overland flow onto the floodplain vary greatly.

Two Examples • As usual, we will have some examples and similar class work

Slides: 10

Download presentation

End of Chapter 4 Movement of a Flood Wave and begin Chapter 7 Open Channel Flow, Manning’s Eqn. Overland Flow

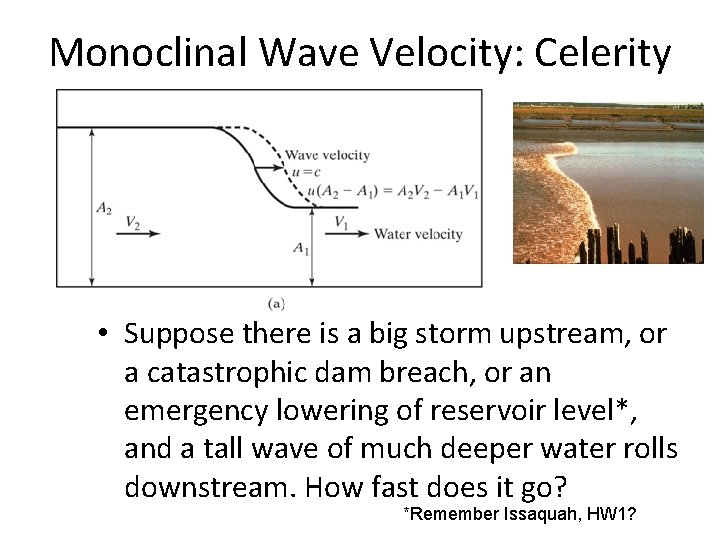
Monoclinal Wave Velocity: Celerity • Suppose there is a big storm upstream, or a catastrophic dam breach, or an emergency lowering of reservoir level*, and a tall wave of much deeper water rolls downstream. How fast does it go? *Remember Issaquah, HW 1?

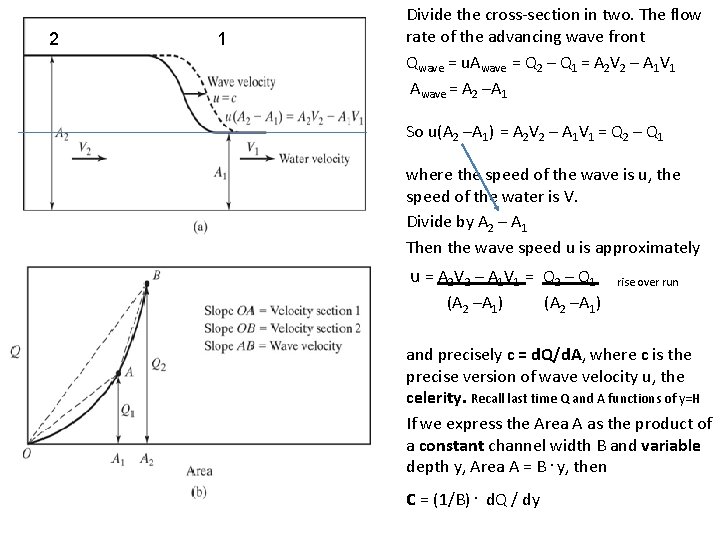
• • Divide the cross-section in two. The flow rate of the advancing wave front Qwave = u. Awave = Q 2 – Q 1 = A 2 V 2 – A 1 V 1 Awave = A 2 –A 1 • So u(A 2 –A 1) = A 2 V 2 – A 1 V 1 = Q 2 – Q 1 • where the speed of the wave is u, the speed of the water is V. Divide by A 2 – A 1 Then the wave speed u is approximately • 2 1 • • u = A 2 V 2 – A 1 V 1 = Q 2 – Q 1 • and precisely c = d. Q/d. A, where c is the precise version of wave velocity u, the celerity. Recall last time Q and A functions of y=H If we express the Area A as the product of a constant channel width B and variable depth y, Area A = B. y, then • (A 2 –A 1) • c = (1/B). d. Q / dy rise over run (A 2 –A 1)

Manning’s Equation • The average velocity V in an open channel is given by Manning’s equation: • where R (the hydraulic radius) = A/P [length], and • A = cross sectional Area [length 2] • P = wetted Perimeter [length] • S = the energy slope [length/length] • n = Manning’s Roughness [unitless] • k = 1. 49 [ft 1/3 /sec] or 1. 0 [m 1/3 /sec] for SI

Manning’s for a wide rectangular channel • Here wetted perimeter P is mostly B, • the cross-sectional area is A = B. y • so the hydraulic radius R = y approximately • Multiplying Manning’s by the area = By gives the flow rate Q • where Q and y are the only variables.

Celerity • If we differentiate the flow form of Manning’s we can evaluate the celerity. Since R ~ y everything to the right of B is a Manning velocity so Monoclinal waves move 5/3 faster than the stream water.

Steady Flow • Now, lets jump to Chapter 7 and continue our use of Manning’s Equation. Steady-state flow refers to the condition where the fluid properties at a point in the system do not change over time. Uniform flow is prismatic flow (flow in prismatic channels: constant cross section and slope) for which the slope of total energy (EGL slope) equals bottom slope.

Normal Depth • Uniform flow problems use Manning’s to compute Normal depth yn, the only depth where flow is uniform. • Normal depth depends on channel geometry and the roughness coefficient, n

Overland Flow Manning’s n Roughness coefficients for overland flow onto the floodplain vary greatly.

Two Examples • As usual, we will have some examples and similar class work / homework. • Example 7. 1 calculates normal depth in a rectangular channel given n and the flow rate. • Example 7. 3 calculates normal flow rate given normal depth in a trapezoidal channel