Enclosure Fire Dynamics Chapter 1 Introduction Chapter 2

Enclosure Fire Dynamics ¢ ¢ ¢ ¢ ¢ Chapter 1: Introduction Chapter 2: Qualitative description of enclosure fires Chapter 3: Energy release rates, Design fires Chapter 4: Plumes and flames Chapter 5: Pressure and vent flows Chapter 6: Gas temperatures (Chapter 7: Heat transfer) Chapter 8: Smoke filling (Chapter 9: Products of combustion) Chapter 10: Computer modeling

Overview General on smoke control in buildings ¢ Examples of applications ¢ Derivation of conservation equations ¢ Smoke filling in small room with small opening: Zukoski method ¢ Smoke filling in large room with large opening: Steady-state method ¢ • Natural ventilation • Mechanical ventilation • Pressurization of lower layer

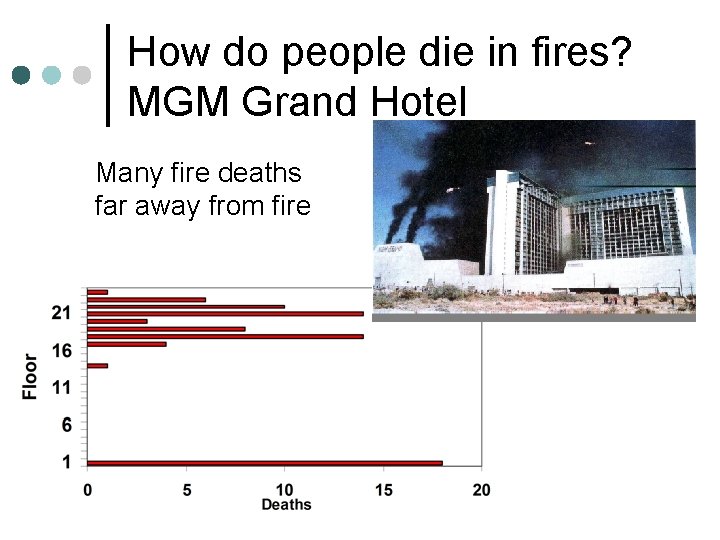
How do people die in fires? MGM Grand Hotel Many fire deaths far away from fire

Reasons for smoke control Life safety – maintain the escape path as long as possible ¢ Firefighter safety – improve visibility ¢ Firefighter operations – reduce time to put out fire ¢ Property protection – reduce smoke damage ¢ Property protection – reduce temperature and external radiation to fuel packages ¢ Continuity of operations = Open for business sooner ¢

Smoke management – preventing smoke spread ¢ Smoke control l ¢ Use of mechanical fans for pressurization Smoke and heat venting Natural (link operated vents) l Mechanical l

Locations for smoke control Atria ¢ Warehouses (rack storage) ¢ High rise buildings (stairwells) ¢ Shopping malls ¢ Performance based designs ¢ Increase travel distance l Substitute for rated construction (smoke barriers) l ¢ Elevators for egress

Example: Atria Atrium – singular (one) ¢ Atria – plural (many) ¢ Opening through floors ¢

Example: Atrium

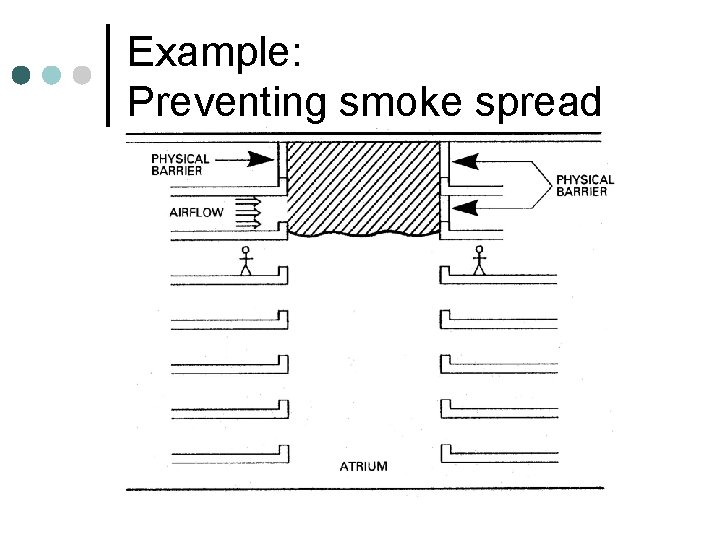
Example: Preventing smoke spread

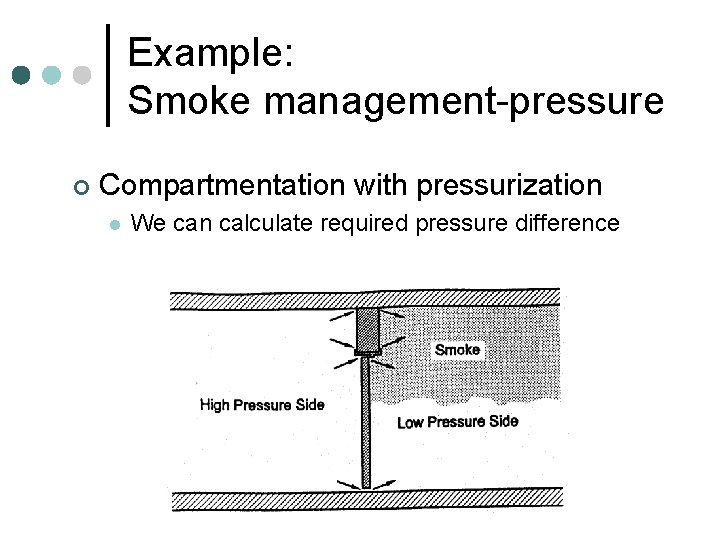
Example: Smoke management-pressure ¢ Compartmentation with pressurization l We can calculate required pressure difference

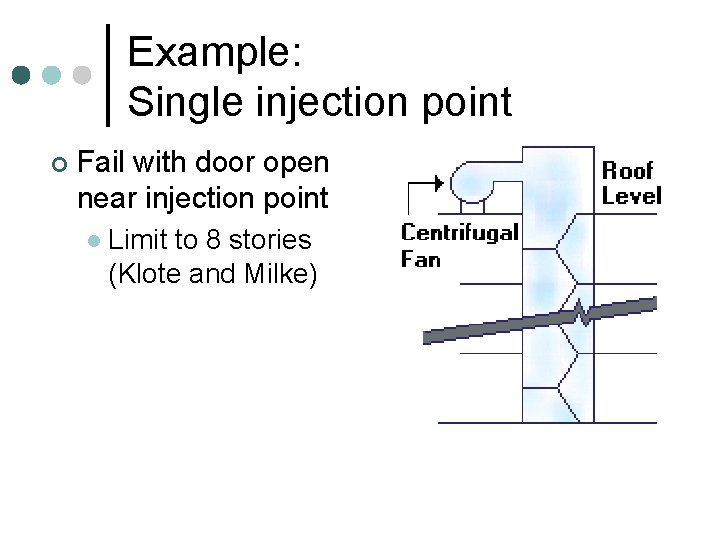
Example: Single injection point ¢ Fail with door open near injection point l Limit to 8 stories (Klote and Milke)

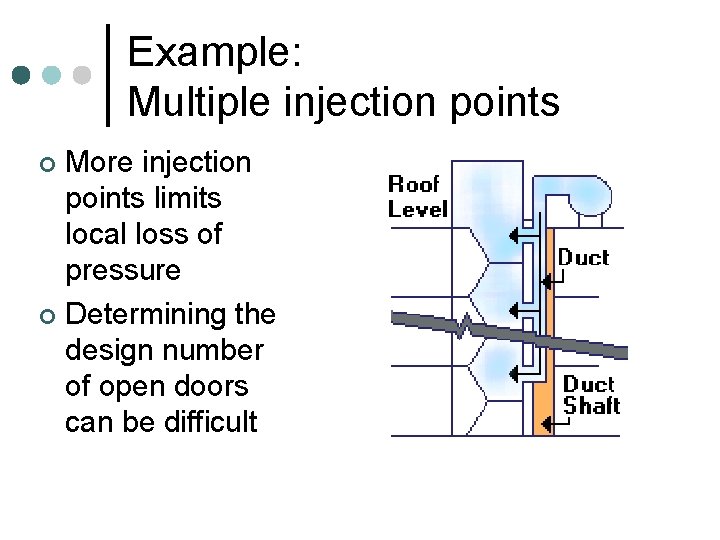
Example: Multiple injection points More injection points limits local loss of pressure ¢ Determining the design number of open doors can be difficult ¢

Example: Smoke control by air flow ¢ Airflow without barriers can control smoke if the air velocity is sufficient l Not usually a recommended method (expensive) l Airflow can enhance burning rate

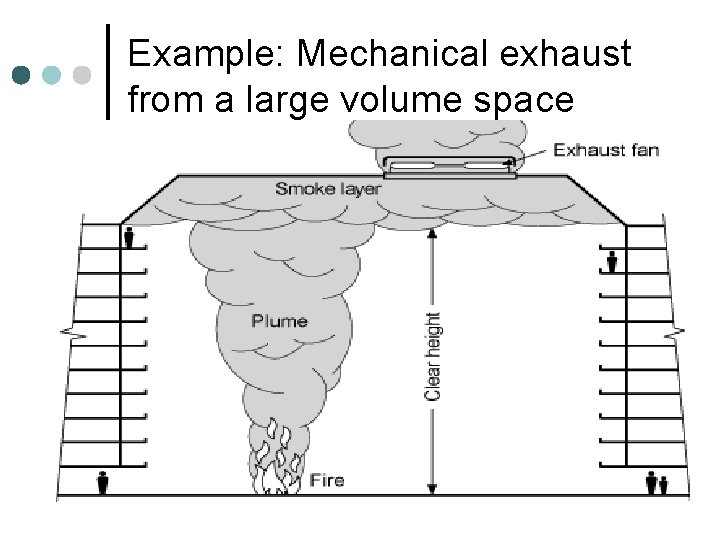
Example: Mechanical exhaust from a large volume space

Example: Balcony spill plume ¢ In many cases, the mass flow rate is larger than from an axi-symmetric plume

Example: Roof vents

Example: Natural smoke venting Reduced flow due to obstructions, wind and sprinklers ¢ Makeup (replacement) air required ¢

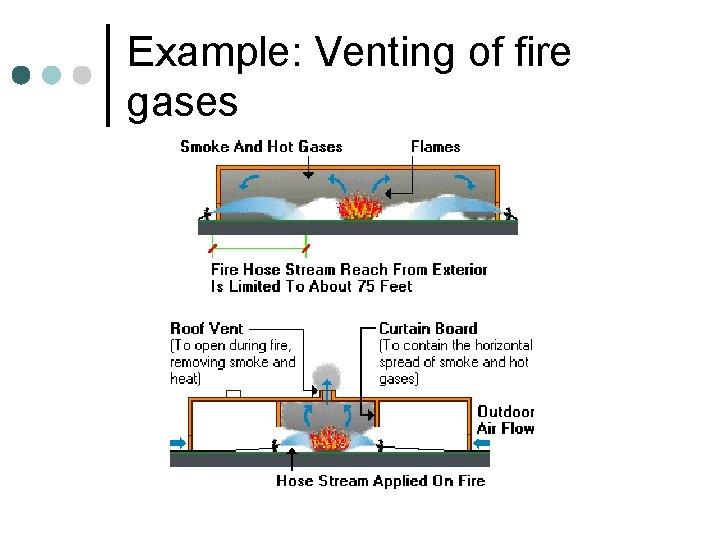
Example: Venting of fire gases

Activation of smoke control system ¢ Smoke detector Thermal detector l Smoke density detector l • Specified optical density/obscuration ¢ Beam detectors • Specified optical density/obscuration ¢ Avoid manual activation, but provide manual activation for fire department

Overview General on smoke control in buildings ¢ Examples of applications ¢ Derivation of conservation equations ¢ Smoke filling in small room with small opening: Zukoski method ¢ Smoke filling in large room with large opening: Steady-state method ¢ • Natural ventilation • Mechanical ventilation • Pressurization of lower layer

Conservation equations Conservation of mass (C of M) ¢ Conservation of energy (C of E) ¢ Conservation of momentum ¢ Conservation of species ¢ l (O 2, CO 2, H 2 O, soot, fuel)

Compartment Fire Environment

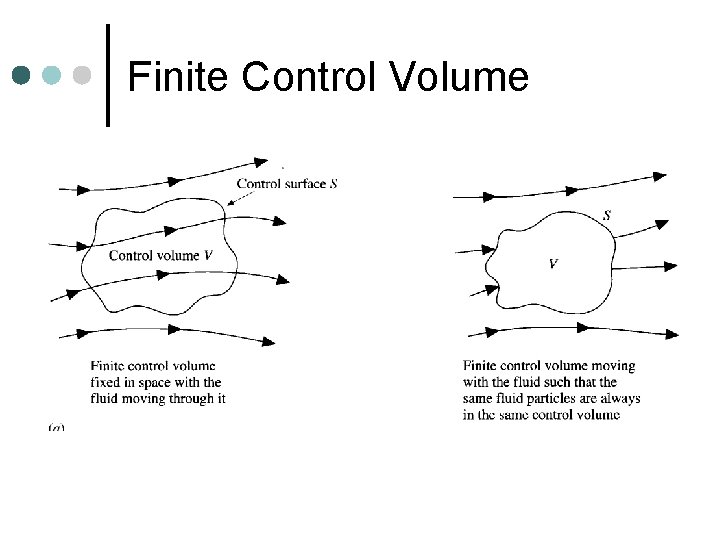
Finite Control Volume

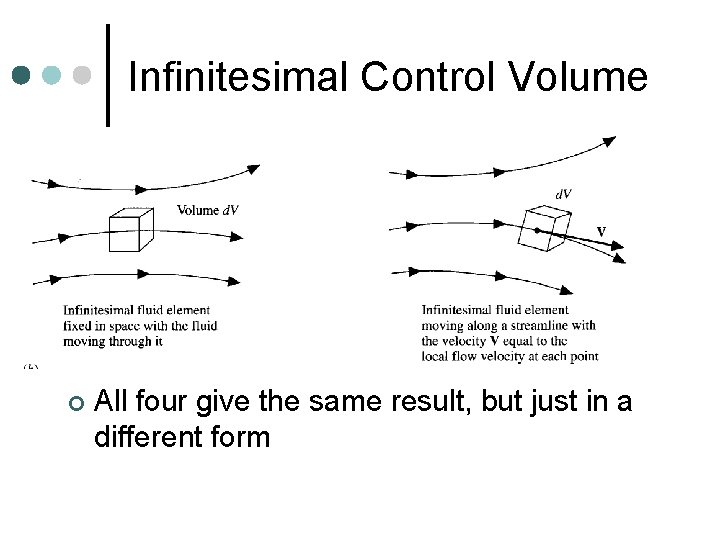
Infinitesimal Control Volume ¢ All four give the same result, but just in a different form

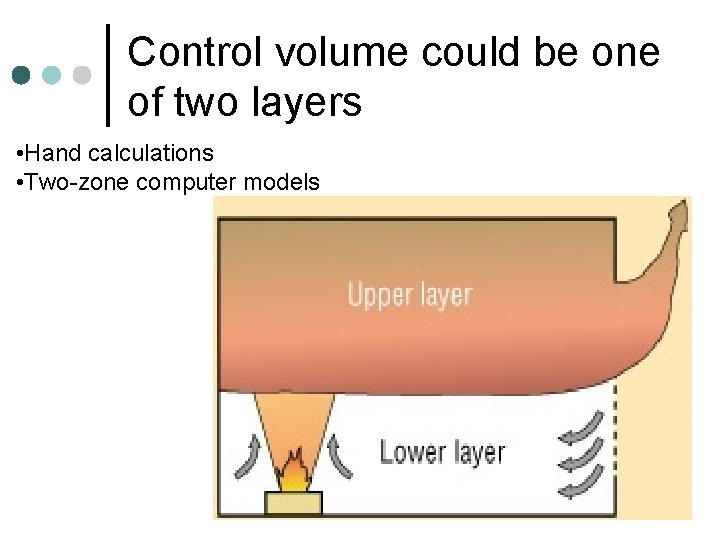
Control volume could be one of two layers • Hand calculations • Two-zone computer models

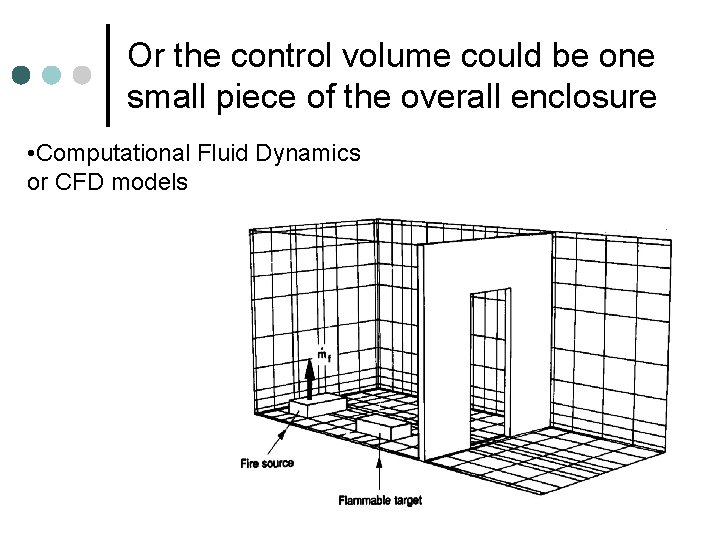
Or the control volume could be one small piece of the overall enclosure • Computational Fluid Dynamics or CFD models

Control surface Surface defining a control volume ¢ Mass, energy etc. pass through the control surface ¢

Overview General on smoke control in buildings ¢ Examples of applications ¢ Derivation of conservation equations ¢ Smoke filling in small room with small opening: Zukoski method ¢ Smoke filling in large room with large opening: Steady-state method ¢ • Natural ventilation • Mechanical ventilation • Pressurization of lower layer

Smoke filling in a room with a small opening (vent) ¢ ¢ Conservation of mass CV is lower layer Plume is ignored or could be included in upper layer Mass leaves CV through plume and vent (positive)

Smoke filling in a room with a small opening (vent) ¢ Remember the Zukoski plume equation ¢ Use the energy equation to find ¢ Substitute equation and into C of M

Smoke filling in a room with a small opening (vent) ¢ ¢ A numerical/graphical solution is possible Generalize results by using dimensionless numbers

Non-dimensional smoke filling equation ¢ Dimensionless height: ¢ Dimensionless HRR: ¢ Dimensionless time: ¢ Dimensionless form of smoke filling equation

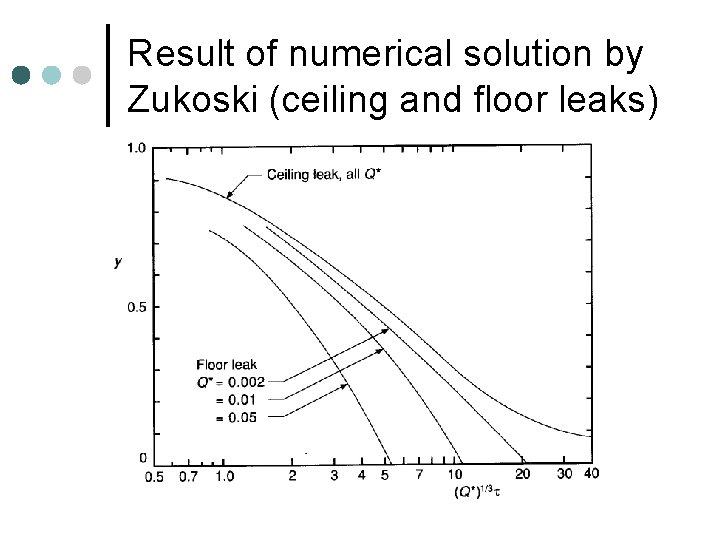
Result of numerical solution by Zukoski (ceiling and floor leaks)

Limitations of Zukoski model ¢ ¢ Small room and small opening Zukoski plume equation l Valid for weak sources ¢ No heat loss No pressure change with time Uniform pressure throughout room ¢ Expect approximate results only ¢ ¢

Overview General on smoke control in buildings ¢ Examples of applications ¢ Derivation of conservation equations ¢ Smoke filling in small room with small opening: Zukoski method ¢ Smoke filling in large room with large opening: Steady-state method ¢ • Natural ventilation • Mechanical ventilation • Pressurization of lower layer

Steady state smoke control ¢ ¢ Spaces are typically large (tall) Openings are large, so there is little (no) pressure buildup inside enclosure l l ¢ Two direction vent flow l ¢ Flow rates through vents are a function of hydrostatic pressure differences Pressure difference varies over height of opening More directions possible with smoke filling in second compartment C of M and C of E equations coupled l Must solve at the same time

Steady state smoke control ¢ Now do something to stop the upper layer from descending (moving) l ¢ Steady state l ¢ Rate of smoke venting (exhaust) equals rate of smoke production (entrainment in plume) Conditions no longer changing with time Method of Tanaka and Yamana

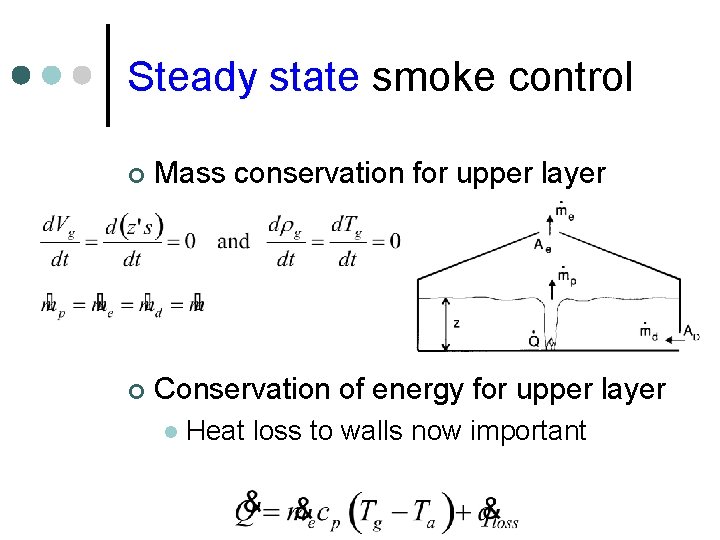
Steady state smoke control ¢ Mass conservation for upper layer ¢ Conservation of energy for upper layer l Heat loss to walls now important

Steady state smoke control ¢ We already solved this energy equation in Chapter 6 l l But now we know z’, so we know the area of the wall being heated, Aw Semi-infinite solid with Tg=Ts

Look at three cases for removing smoke Natural ventilation ¢ Mechanical ventilation ¢ Pressurization of lower layer ¢

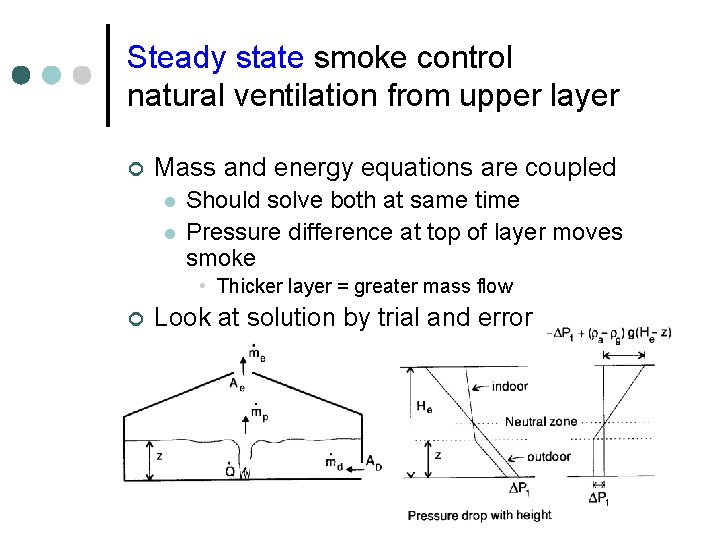
Steady state smoke control natural ventilation from upper layer ¢ Mass and energy equations are coupled l l Should solve both at same time Pressure difference at top of layer moves smoke • Thicker layer = greater mass flow ¢ Look at solution by trial and error

Steady state smoke control natural ventilation from upper layer ¢ Trial and error solution l Guess a layer height l Solve mass and energy balances l Correct layer height guess and density l Resolve mass and energy balance

Steady state smoke control mechanical ventilation from upper layer ¢ A fan is now placed at the top of the compartment to remove smoke l Generally know the fan exhaust rate [m 3/s]

Steady state smoke control mechanical ventilation from upper layer

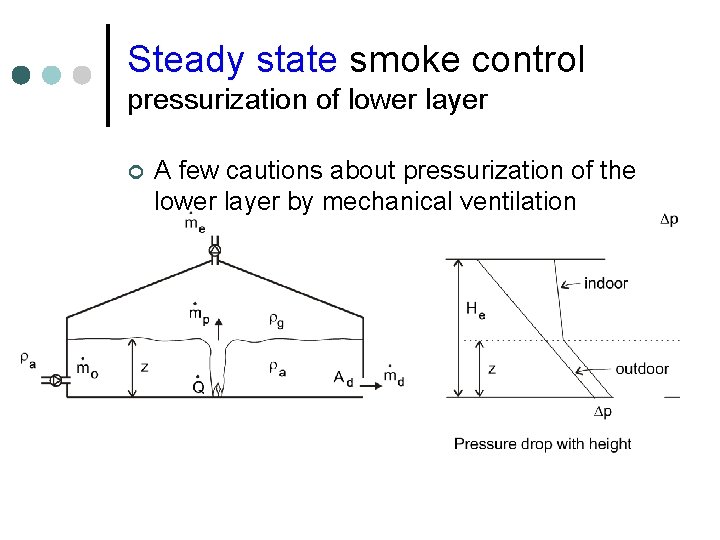
Steady state smoke control pressurization of lower layer ¢ A few cautions about pressurization of the lower layer by mechanical ventilation

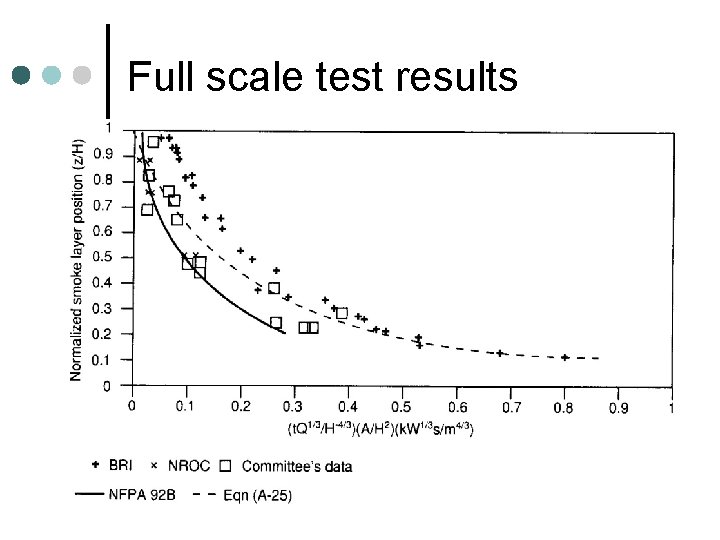
Full scale test results

Some final cautions ¢ ¢ ¢ There is not universal agreement by fire researchers on these equations Some, but not much, full scale testing Fire model results versus correlations l l Sometimes easier to just use a fire model Some models have been validated (tested) under smoke control conditions

Any questions?