Enclosure Fire Dynamics Chapter 1 Introduction Chapter 2

Enclosure Fire Dynamics ¢ ¢ ¢ ¢ ¢ Chapter 1: Introduction Chapter 2: Qualitative description of enclosure fires Chapter 3: Energy release rates, Design fires Chapter 4: Plumes and flames Chapter 5: Pressure and vent flows Chapter 6: Gas temperatures (Chapter 7: Heat transfer) Chapter 8: Smoke filling (Chapter 9: Products of combustion) Chapter 10: Computer modeling

Goals and expectations ¢ ¢ ¢ Flames l Calculate flame heights Plumes l Calculate plume mass flow (function of height z) l Calculate plume centerline temperature (fnct of z) l Know Zukoski plume and Heskestad plume Ceiling Jets l Use Alperts correlations

Define mean flame height ¢ Height where flame is observed 50% of the time l Height above which flame appears half the time

Froude number in terms of heat release rate ¢ Experiments show mean flame height, L, is a function of the square root of Fr:

Normalized flame height versus dimensionless energy release rate ¢ 1< Q* <1000 ¢ See Table 2 -1. 2 [SFPE] for many different flame height correlations

Flame height correlation of Heskestad ¢ Reliable for 0. 5 < Q* < 1000

Formation of plume and ceiling jet

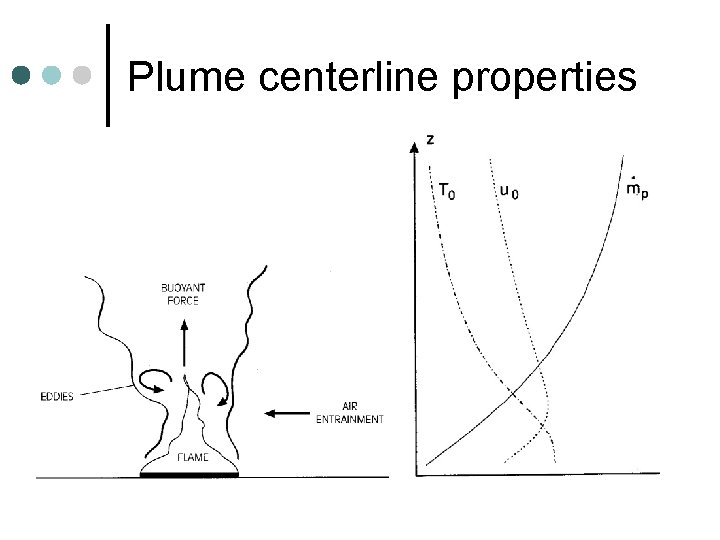
Plume centerline properties

The ideal plume (point source plume) Goal: Derive simple algebraic equations for properties in plume ¢ Assume top hat profile ¢

Derivation of ideal plume equations ¢ Temperature as a function of height l l ¢ Plume radius as a function of height l ¢ b(z) [m] Upward velocity as a function of height l ¢ Difference above T T(z) [o. C or K] u(z) [m/s] Plume mass flow rate as a function of height l [kg/s]

Final form of the equations:

Zukoski Plume ¢ Adjusted ideal plume theory to fit with experiments ¢ Generally underestimates plume mass flow rate

Zukoski plume experiments

Plume equations that better represent reality Many researchers have worked on developing plume equations ¢ Derive through dimensional analysis and experiment ¢ Heskestad plume equations l Mc. Caffrey plume equations l etc l

Heskestad; virtual origin

Heskestad plume correlations z>L z<L

Measurements of centerline temperatures

Plume interaction with a ceiling Forms a ceiling jet (CJ) ¢ Velocity of CJ driven by buoyancy of plume ¢ Just as with plumes, there a number of different CJ correlations ¢

Temperature and velocity cross sections are not necessarily the same Depth of CJ in the range 5%-12% of H ¢ Maximum u and T very near ceiling ( 1% of H) ¢

Alpert correlations r/H<0. 18 r/H>0. 18 r/H<0. 15 r/H>0. 15

Any questions? Next: Unit 5 – Vent flows