ENCE 710 Design of Steel Structures IV COMPOSITE









- Slides: 16

ENCE 710 Design of Steel Structures IV. COMPOSITE STEEL-CONCRET CONSTRUCTION C. C. Fu, Ph. D. , P. E. Civil and Environmental Engineering Department University of Maryland

Introduction Following subjects are covered: n Composite Action n Effective Width n Nominal Moment Strength n Shear Connectors, Strength and Fatigue n Formed Steel Deck Reading: n Chapters 16 of Salmon & Johnson n AISC LRFD Specification Chapters B (Design Requirements) and I (Design of Composite Members) 2

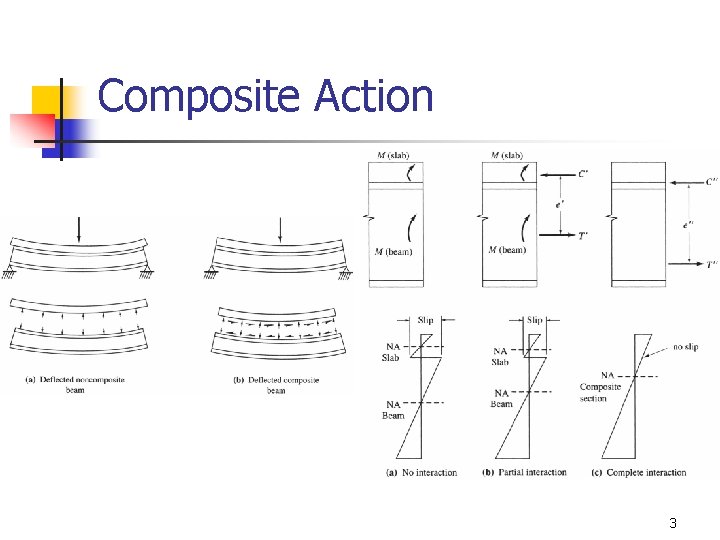
Composite Action 3

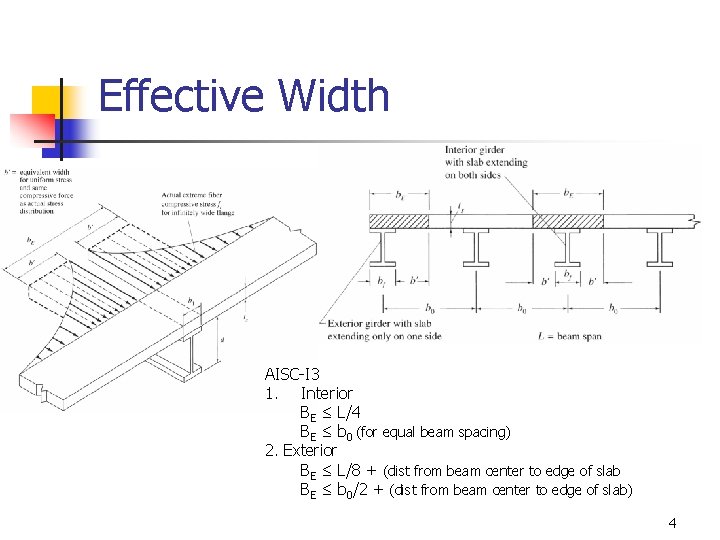
Effective Width AISC-I 3 1. Interior BE ≤ L/4 BE ≤ b 0 (for equal beam spacing) 2. Exterior BE ≤ L/8 + (dist from beam center to edge of slab BE ≤ b 0/2 + (dist from beam center to edge of slab) 4

Nominal Moment Strength of Fully Composite Section (AISC 14 th Edition Art. I 3. 2 a) 1. Mn = based on plastic stress distribution on the Composite Section; Φb = 0. 9 2. Mn = based on superposition of elastic stresses, considering the effect of shoring; Φb = 0. 9 5

Plastic Stress Distribution Case 1 (if a ≤ ts): S & J Eq. (16. 7. 1 to 5) Case 2 (if a > ts): S & J Eq. (16. 7. 6 to 10) 6

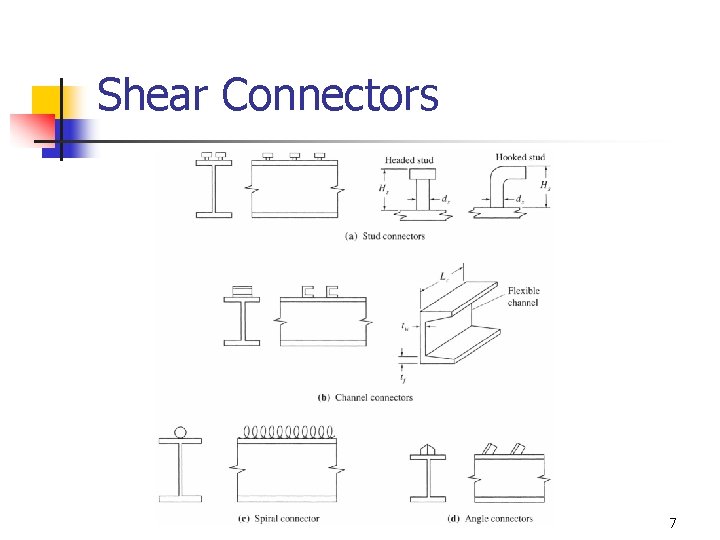
Shear Connectors 7

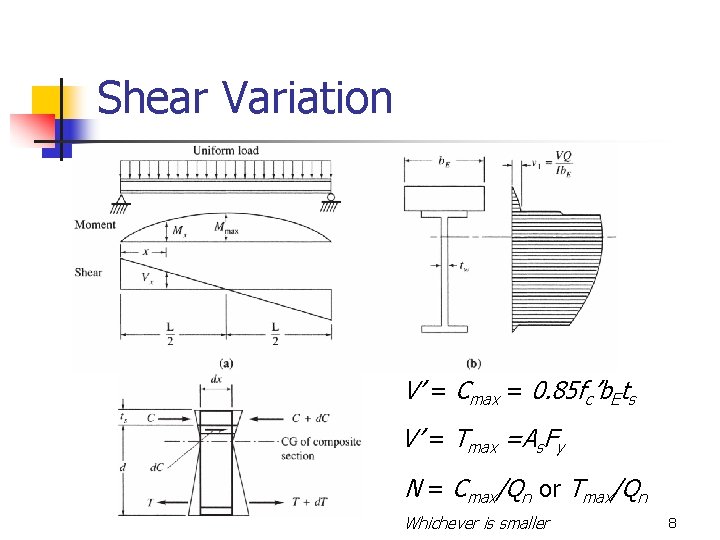
Shear Variation V’ = Cmax = 0. 85 fc’b. Ets V’ = Tmax =As. Fy N = Cmax/Qn or Tmax/Qn Whichever is smaller 8

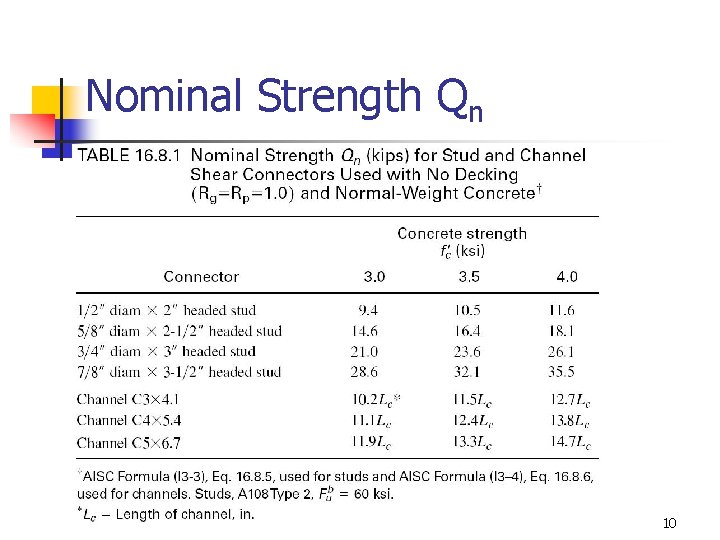
Nominal Strength Qn Qn = 1. Headed Steel Stud (AISC Eq. I 8 -1) 2. Channel Connectors (AISC Eq. I 8 -2) 9

Nominal Strength Qn 10

Connector Design – Fatigue Strength (AASHTO LRFD Eq. 6. 10. 7. 4. 1 b-1) Zr = d 2 5. 5 d 2/2; (AASHTO LRFD Eq. 6. 10. 7. 4. 2 -1) where = 34. 5 – 4. 28 log N (AASHTO LRFD Eq. 6. 10. 7. 4. 2 -2) Example: 11

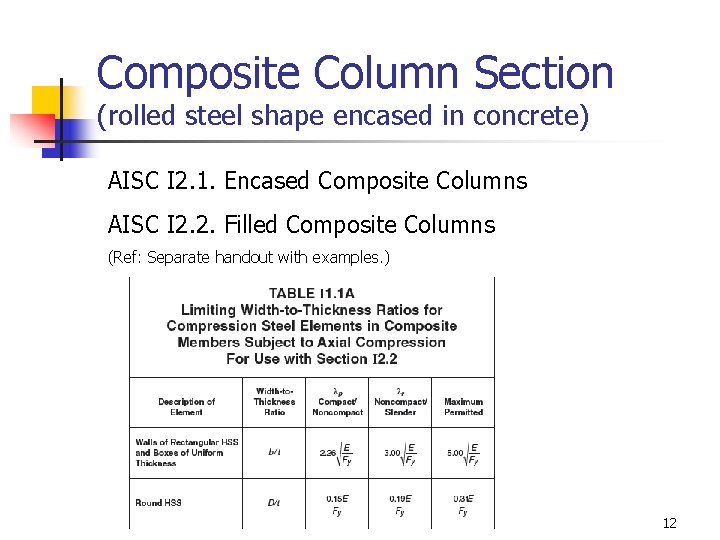
Composite Column Section (rolled steel shape encased in concrete) AISC I 2. 1. Encased Composite Columns AISC I 2. 2. Filled Composite Columns (Ref: Separate handout with examples. ) 12

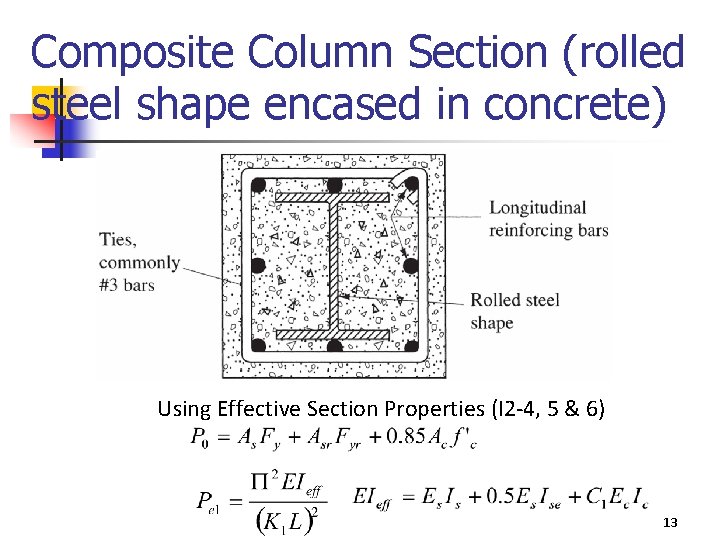
Composite Column Section (rolled steel shape encased in concrete) Using Effective Section Properties (I 2 -4, 5 & 6) 13

Filled Composite Column Example AISC I 2 -2 b (a) Compact (b) Noncompact (c) Slender 14

Filled Composite Column Example • For compact sections • Ac = bfhf+π(r-t)2+2 bf(r-t)+2 hf(r-t) Ac = (8. 5 in. )(4. 5 in. ) + π(0. 375 in. )2 + (8. 5 in. )(0. 375 in. ) + 2(4. 5 in. )(0. 375 in. ) = 48. 4 in. 2 • • • P 0 = (10. 4 in. 2)(46 ksi) + 0. 85(48. 4 in. 2)(5 ksi) = 684 kips • • EIeff = (29, 000 kis)(61. 8 in. 4) + (0. 90)(3, 900 ksi)(111 in. 4) = 2, 180, 000 kip-in. 2 15

Filled Composite Column Example • Pe = π2(2, 180, 000 kip-in. 2)/(1. 0(14 ft)(12 in. /ft))2 = 762 kips • P 0/Pe = 684 kips/762 kips = 0. 898 ≤ 2. 25 • • φc. Pn = 0. 75(470 kips) = 353 kips > 336 kips o. k. 16