EMT 360364 Control Engineering Transfer Function Transfer Function

EMT 360/364 Control Engineering Transfer Function

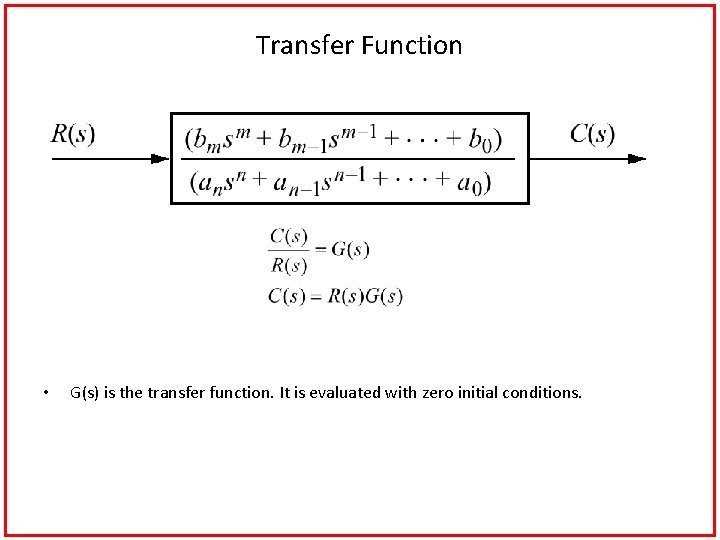
Transfer Function • G(s) is the transfer function. It is evaluated with zero initial conditions.

Transfer Function • Find the transfer function represented by c(t), to an input, r(t) • Taking the Laplace transform, The transfer function G(s), is

Transfer Function • From the previous slide, find the response, c(t), to an input, r(t)=u(t), a unit step, assuming zero initial condition. • Since r(t)=u(t), R(s)=1/s Using partial fraction expansion, Taking inverse Laplace,

Transfer Function • In general, a physical system that can be represented by a linear, time invariant differential equation can be modeled as a transfer function. • Transfer function can be used to represent – electrical networks – translational mechanical systems – rotational mechanical systems – electromechanical systems

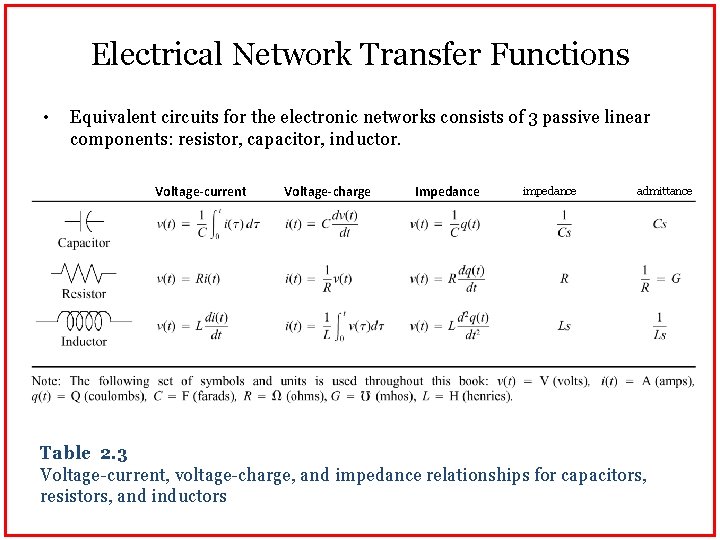
Electrical Network Transfer Functions • Equivalent circuits for the electronic networks consists of 3 passive linear components: resistor, capacitor, inductor. Voltage-current Voltage-charge Impedance impedance admittance Table 2. 3 Voltage-current, voltage-charge, and impedance relationships for capacitors, resistors, and inductors

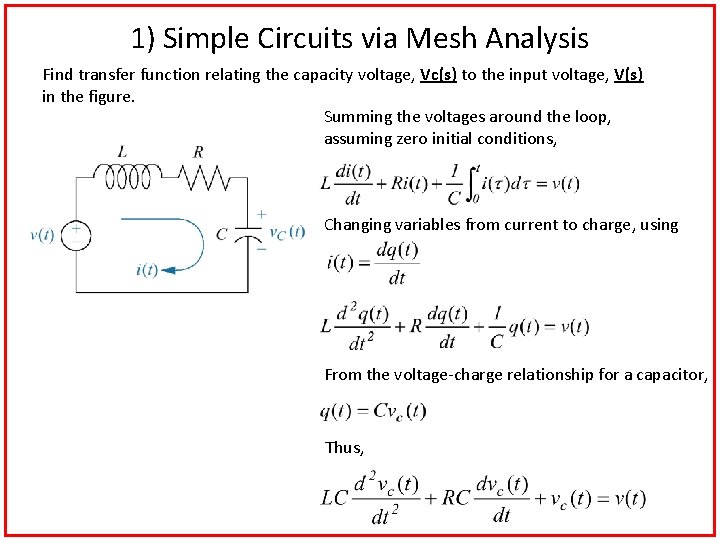
1) Simple Circuits via Mesh Analysis Find transfer function relating the capacity voltage, Vc(s) to the input voltage, V(s) in the figure. Summing the voltages around the loop, assuming zero initial conditions, Changing variables from current to charge, using From the voltage-charge relationship for a capacitor, Thus,

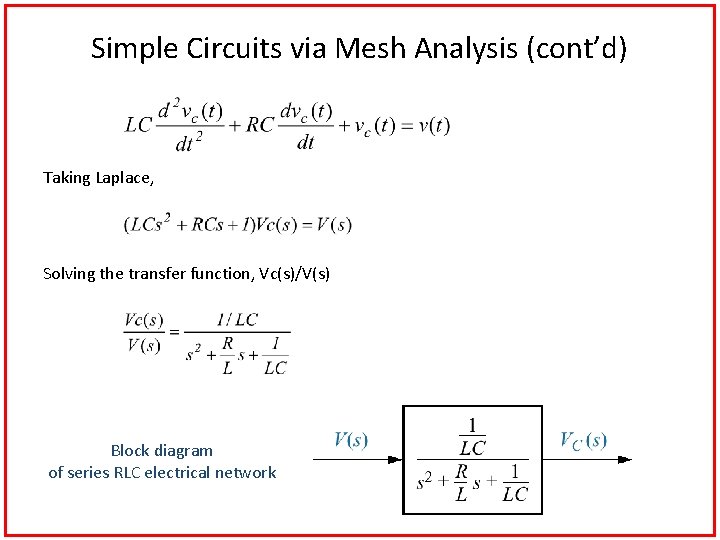
Simple Circuits via Mesh Analysis (cont’d) Taking Laplace, Solving the transfer function, Vc(s)/V(s) Block diagram of series RLC electrical network

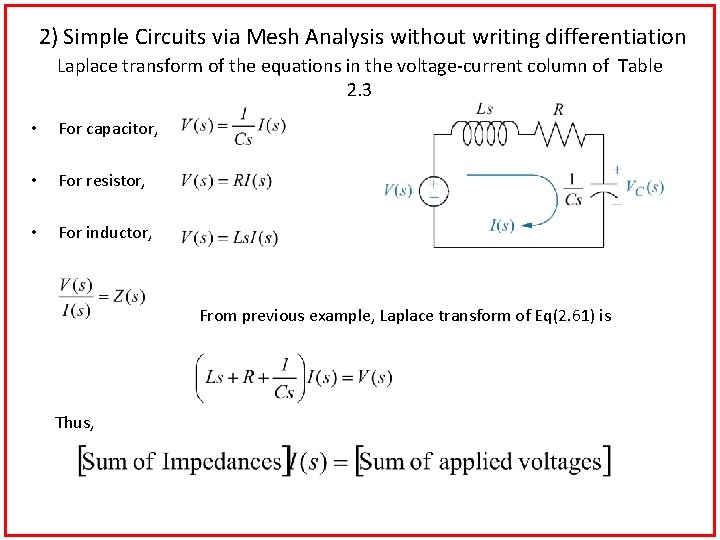
2) Simple Circuits via Mesh Analysis without writing differentiation Laplace transform of the equations in the voltage-current column of Table 2. 3 • For capacitor, • For resistor, • For inductor, From previous example, Laplace transform of Eq(2. 61) is Thus,

Using mesh analysis without writing differentiation, give the same results Solving for I(s)/V(s), For capacitor, Thus,

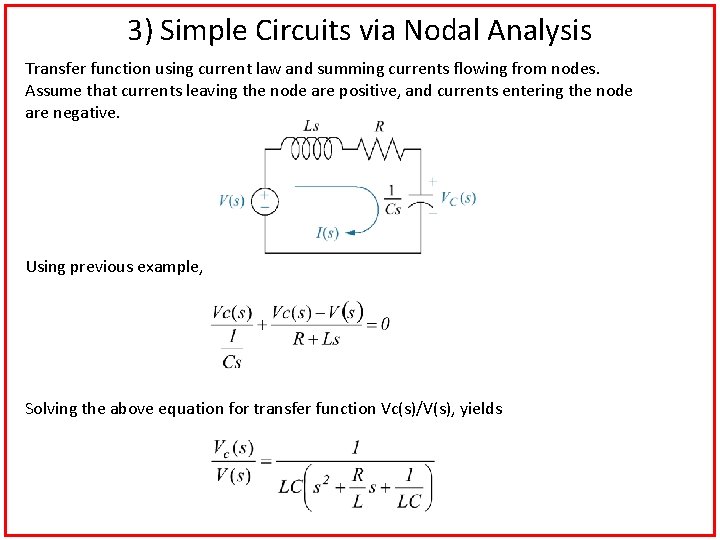
3) Simple Circuits via Nodal Analysis Transfer function using current law and summing currents flowing from nodes. Assume that currents leaving the node are positive, and currents entering the node are negative. Using previous example, Solving the above equation for transfer function Vc(s)/V(s), yields

4) Simple Circuits via Voltage Division Transfer function using voltage division. Using previous example, Solving the above equation for transfer function Vc(s)/V(s), yields

In summary 4 different methods can be used to obtain the transfer function of simple circuits 1) Differential equation derivation using KVL 2) Using mesh analysis with Laplace transform (without writing differential equation) 3) Nodal analysis 4) Voltage divider/division

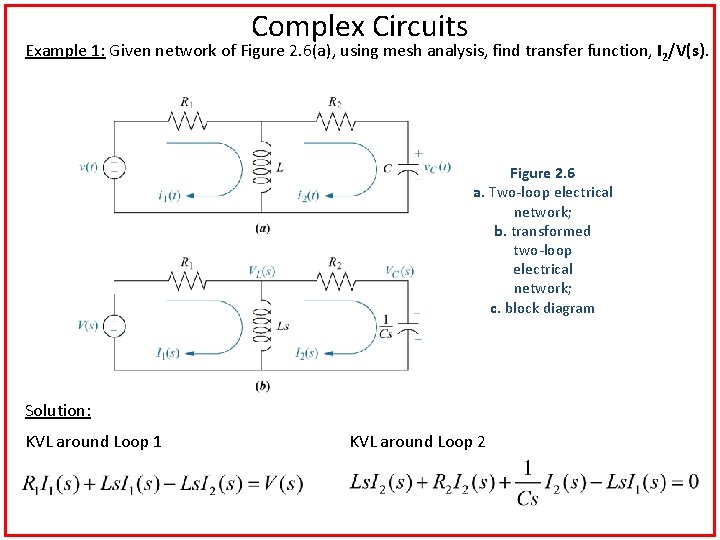
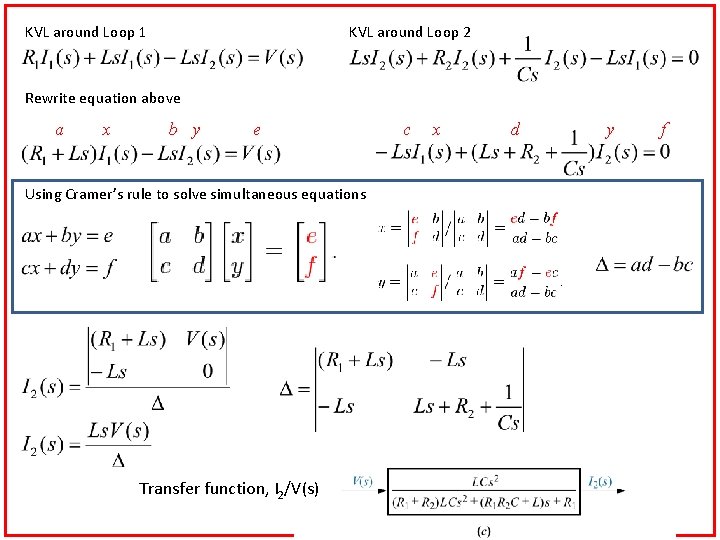
Complex Circuits Example 1: Given network of Figure 2. 6(a), using mesh analysis, find transfer function, I 2/V(s). Figure 2. 6 a. Two-loop electrical network; b. transformed two-loop electrical network; c. block diagram Solution: KVL around Loop 1 KVL around Loop 2

KVL around Loop 1 KVL around Loop 2 Rewrite equation above a x b y e Using Cramer’s rule to solve simultaneous equations Transfer function, I 2/V(s) c x d y f

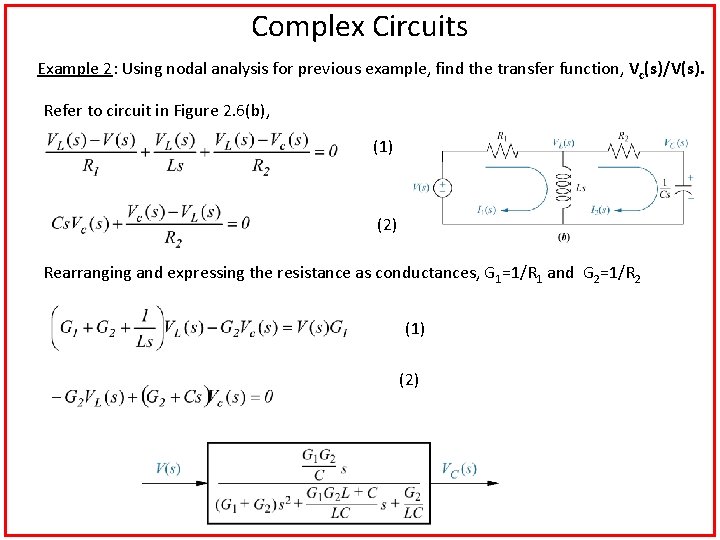
Complex Circuits Example 2: Using nodal analysis for previous example, find the transfer function, Vc(s)/V(s). Refer to circuit in Figure 2. 6(b), (1) (2) Rearranging and expressing the resistance as conductances, G 1=1/R 1 and G 2=1/R 2 (1) (2)

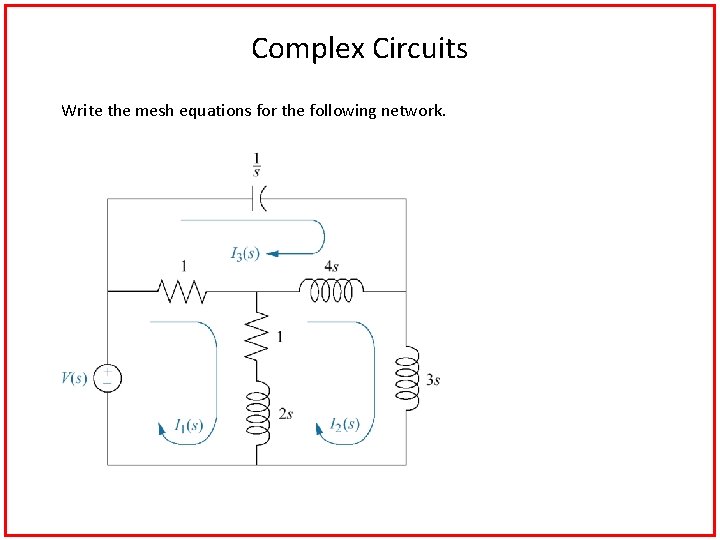
Complex Circuits Write the mesh equations for the following network.

Complex Circuits

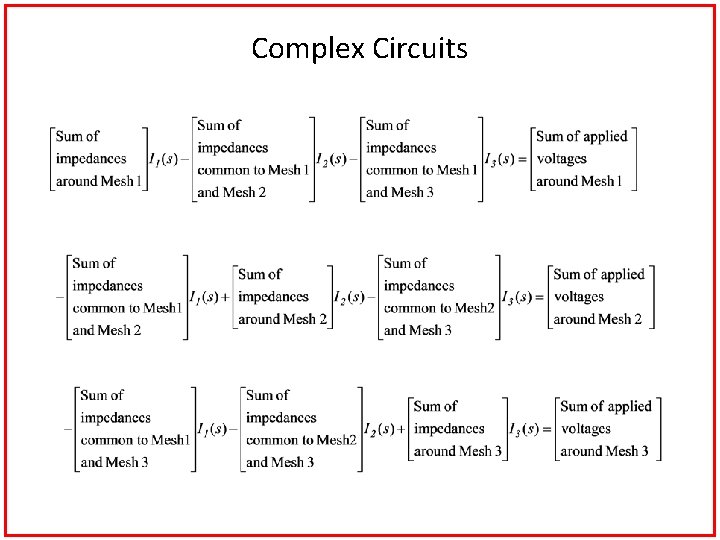
Complex Circuits Mesh equations:

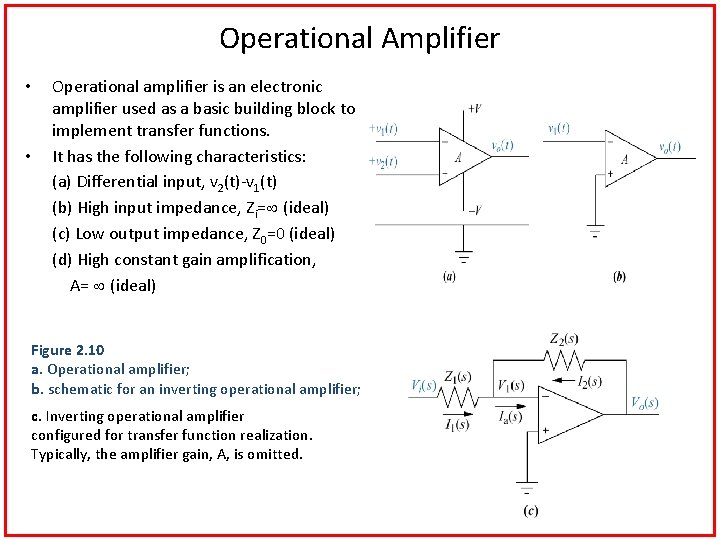
Operational Amplifier Operational amplifier is an electronic amplifier used as a basic building block to implement transfer functions. • It has the following characteristics: (a) Differential input, v 2(t)-v 1(t) (b) High input impedance, Zi= (ideal) (c) Low output impedance, Z 0=0 (ideal) (d) High constant gain amplification, A= (ideal) • Figure 2. 10 a. Operational amplifier; b. schematic for an inverting operational amplifier; c. Inverting operational amplifier configured for transfer function realization. Typically, the amplifier gain, A, is omitted.

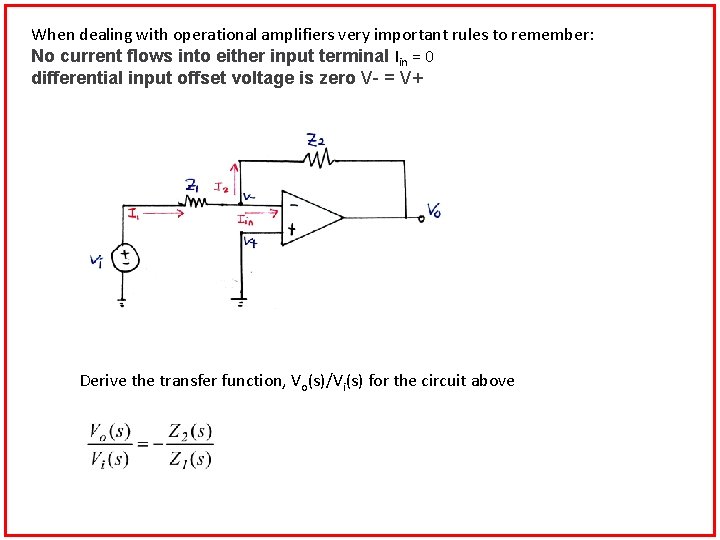
When dealing with operational amplifiers very important rules to remember: No current flows into either input terminal Iin = 0 differential input offset voltage is zero V- = V+ Derive the transfer function, Vo(s)/Vi(s) for the circuit above

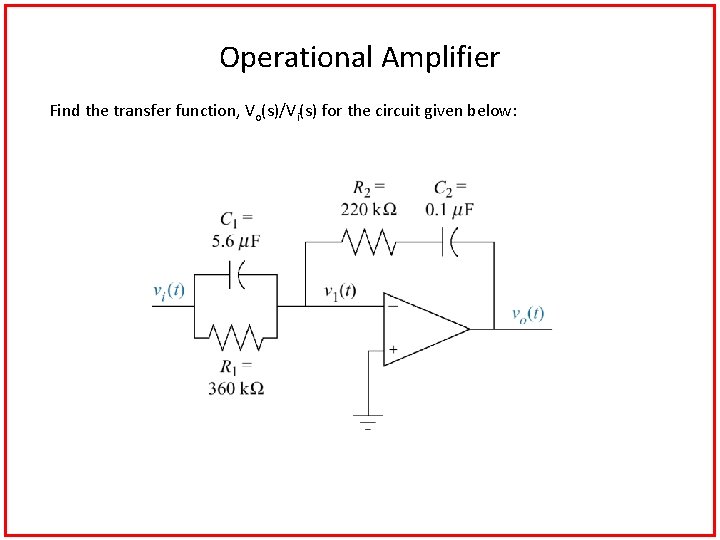
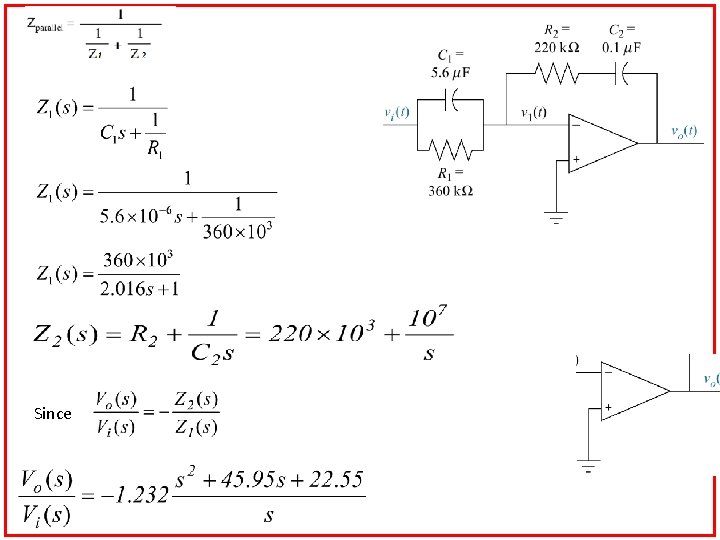
Operational Amplifier Find the transfer function, Vo(s)/Vi(s) for the circuit given below:

R Since

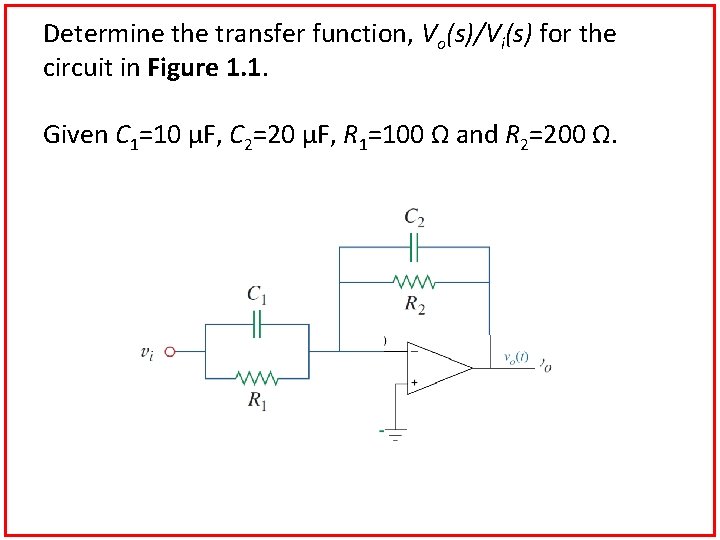
Determine the transfer function, Vo(s)/Vi(s) for the circuit in Figure 1. 1. Given C 1=10 µF, C 2=20 µF, R 1=100 Ω and R 2=200 Ω.

Modelling Mechanical System Determine the differential equations that model the behaviour of a mechanical system 1. Elements making up a mechanical system 2. Modelling examples 3. Transmitting and converting motion

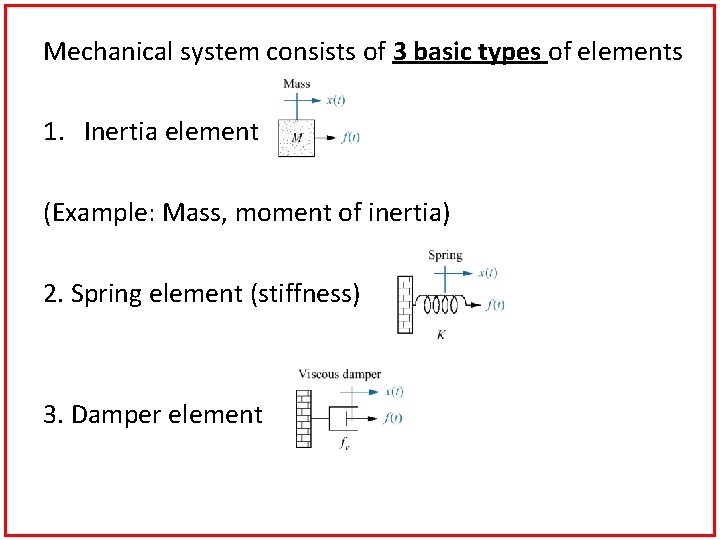
Mechanical system consists of 3 basic types of elements 1. Inertia element (Example: Mass, moment of inertia) 2. Spring element (stiffness) 3. Damper element

Mechanical Components

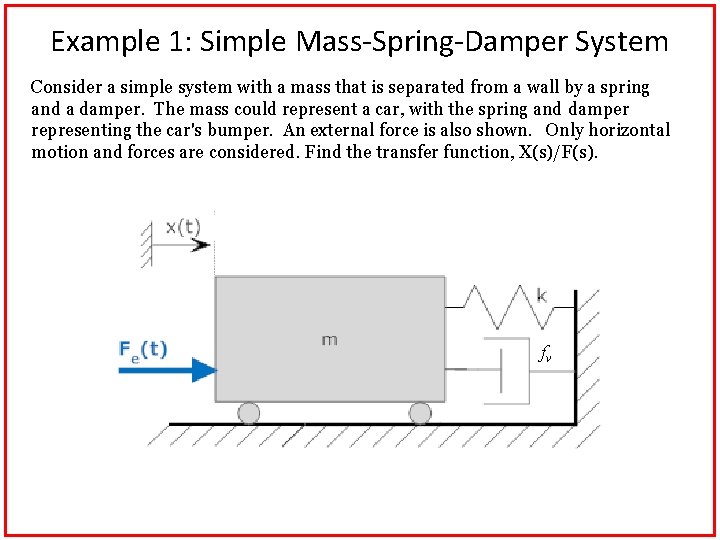
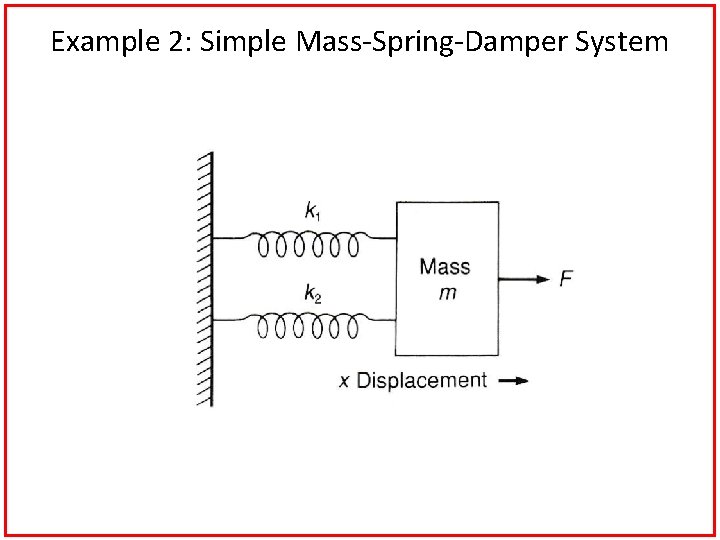
Example 1: Simple Mass-Spring-Damper System Consider a simple system with a mass that is separated from a wall by a spring and a damper. The mass could represent a car, with the spring and damper representing the car's bumper. An external force is also shown. Only horizontal motion and forces are considered. Find the transfer function, X(s)/F(s). fv

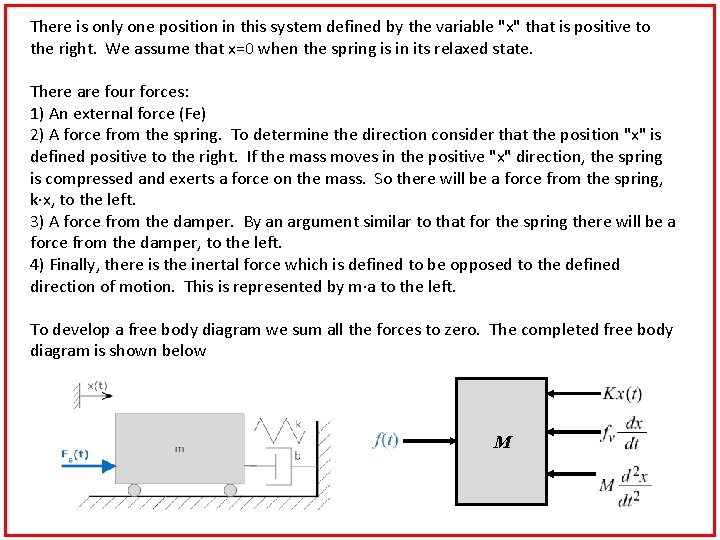
There is only one position in this system defined by the variable "x" that is positive to the right. We assume that x=0 when the spring is in its relaxed state. There are four forces: 1) An external force (Fe) 2) A force from the spring. To determine the direction consider that the position "x" is defined positive to the right. If the mass moves in the positive "x" direction, the spring is compressed and exerts a force on the mass. So there will be a force from the spring, k·x, to the left. 3) A force from the damper. By an argument similar to that for the spring there will be a force from the damper, to the left. 4) Finally, there is the inertal force which is defined to be opposed to the defined direction of motion. This is represented by m·a to the left. To develop a free body diagram we sum all the forces to zero. The completed free body diagram is shown below M

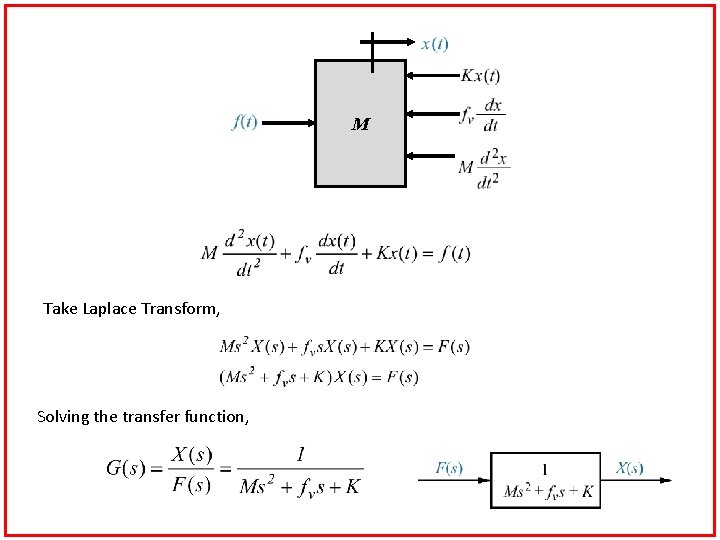
M Take Laplace Transform, Solving the transfer function,

Example 2: Simple Mass-Spring-Damper System

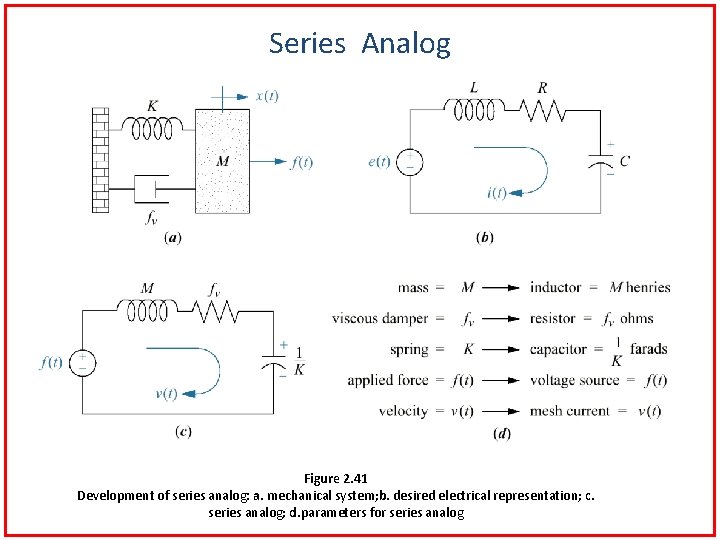
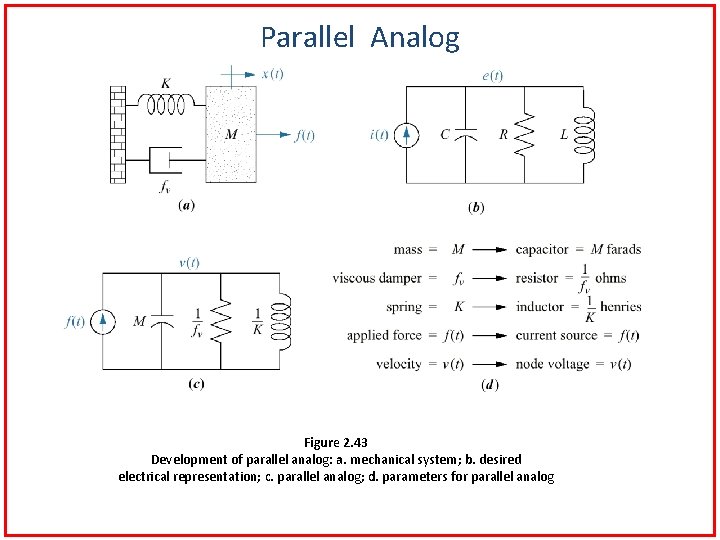
Electric Circuit Analogs • Converting mechanical systems to electrical networks before writing the describing equations is an alternative problem solving approach. • An electric circuit that is analogous to a system from another discipline is called an electric circuit analog. • When compared with mesh equations, the resulting electrical circuit is called series analog. • When compared with nodal equations, the resulting electrical circuit is called parallel analog.

Series Analog Figure 2. 41 Development of series analog: a. mechanical system; b. desired electrical representation; c. series analog; d. parameters for series analog

Consider the mechanical system in Figure 2. 41(a): Kirchhoff’s mesh equation for the simple RLC network in Figure 2. 41(b): Displacement and current are not analogous. A direct analogy can be created by converting displacement to velocity by dividing and multiplying the left hand side by s, yielding Comparing the equations, the sum of impedance is recognized and a circuit shown in Figure 2. 41 (c) can be drawn.

Parallel Analog Figure 2. 43 Development of parallel analog: a. mechanical system; b. desired electrical representation; c. parallel analog; d. parameters for parallel analog

Parallel Analog Consider mechanical system in Figure 2. 43 (a), whose equation of motion is: Kirchhoff’s nodal equation for a simple RLC network in Figure 2. 43 (b) is: Identify the sum of admittance and a circuit in Figure 2. 43 (c) can be drawn.