EMT 272297 Semiconductor Fundamentals Chapter 2 b Semiconductor

EMT 272/297 Semiconductor Fundamentals Chapter 2 b Semiconductor in Equilibrium

Semiconductor in Equilibrium Charge Carriers in Semiconductors ◦ ◦ Equilibrium Distribution of Electrons and Holes The no and po Equations The Intrinsic Carrier Concentration The Intrinsic Fermi-Level Position Dopant Atoms and Energy Levels ◦ Qualitative Description ◦ Ionization Energy ◦ Group III-V semiconductors The Extrinsic Semiconductor ◦ Equilibrium Distribution of Electrons and Holes ◦ The Product of no and po ◦ Degenerate and Nondegenerate Semiconductors

Semiconductor in Equilibrium Statistic of Donors and Acceptors ◦ Probability Function ◦ Complete Ionization and Freeze-Out Charge neutrality ◦ Compensated Semiconductors ◦ Equilibrium Electron and Hole Concentrations Position of Fermi Energy Level ◦ Mathematical Derivation ◦ Variation of EF with Doping Concentration and Temperature ◦ Relevance of the Fermi Energy

Equilibrium Distribution of Electrons and Holes Charge Carriers in Semiconductors T>0 K Ec Ev Conduction band Valence band ➢Particles that can freely move and contribute to the current flow (conduction) carrier 1. Electron in conduction band 2. Hole in valence band

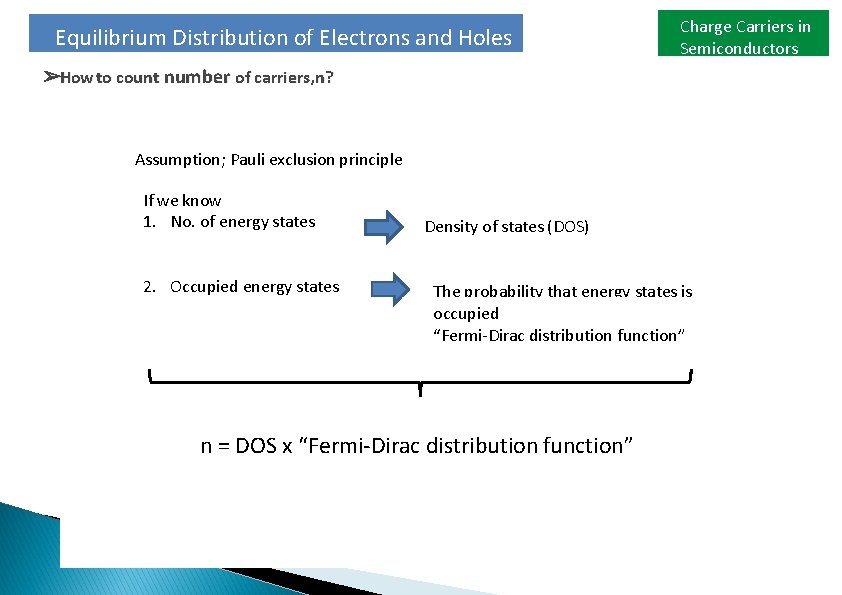
Equilibrium Distribution of Electrons and Holes Charge Carriers in Semiconductors ➢How to count number of carriers, n? Assumption; Pauli exclusion principle If we know 1. No. of energy states 2. Occupied energy states Density of states (DOS) The probability that energy states is occupied “Fermi-Dirac distribution function” n = DOS x “Fermi-Dirac distribution function”

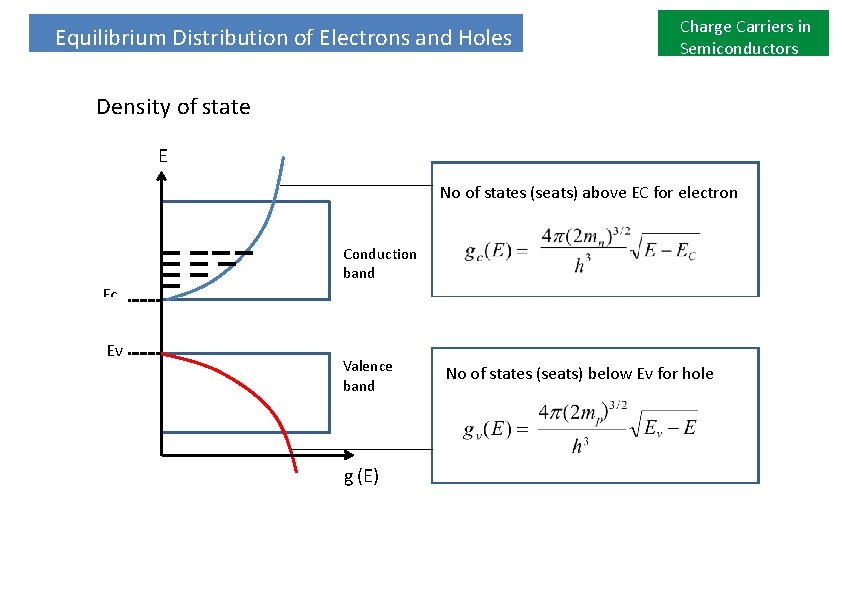
Equilibrium Distribution of Electrons and Holes Charge Carriers in Semiconductors Density of state E No of states (seats) above EC for electron Conduction band Ec Ev Valence band g (E) No of states (seats) below Ev for hole

Charge Carriers in Semiconductors Equilibrium Distribution of Electrons and Holes Fermi-Dirac distribution Probability of electron having certain energy E Electron (blue line) Electron having energy above Ec Ec Fermi energy, EF Ev hole (red line) Hole having energy below Ev 0. 5 1 f (E) EF; the energy below which all states are filled with electron and above which all states are empty at 0 K

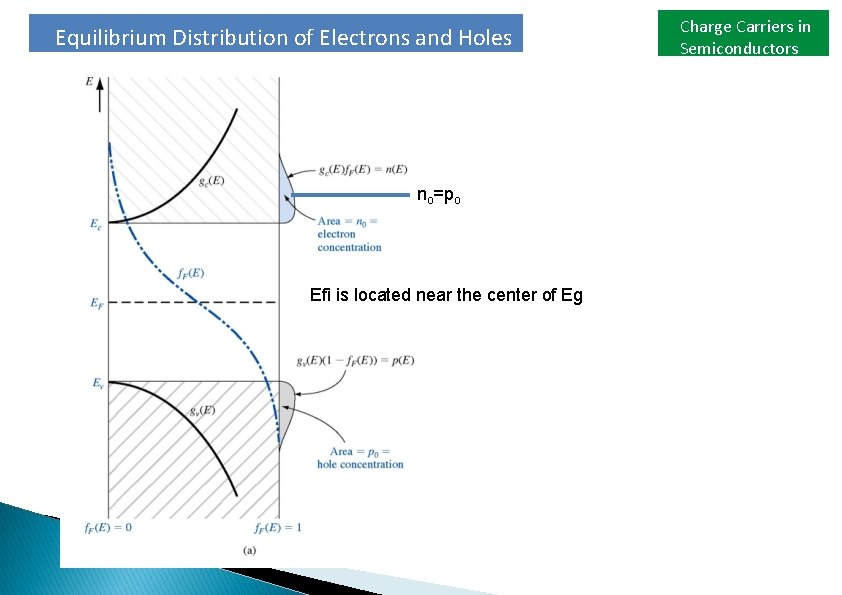
Equilibrium Distribution of Electrons and Holes no=po Efi is located near the center of Eg Charge Carriers in Semiconductors

Charge Carriers in Semiconductors The no and po Equations Thermal equilibrium concentration of electron, no NC ; effective density of states function in conduction band

The no and po Equations Charge Carriers in Semiconductors Q. 1 Calculate thermal equilibrium electron concentration in Si at T= 300 K. Assume that Fermi energy is 0. 25 e. V below the conduction band. The value of Nc for Si at T=300 K is 2. 8 x 1019 cm-3.

Charge Carriers in Semiconductors The no and po Equations Thermal equilibrium concentration of hole, po Nv; effective density of states function in valence band

The no and po Equations Charge Carriers in Semiconductors Q. 2 Calculate thermal equilibrium hole concentration in Si at T= 300 K. Assume that Fermi energy is 0. 27 e. V below the conduction band. The value of Nc for Si at T=300 K is 1. 04 x 1019 cm-3.

The no and po Equations Charge Carriers in Semiconductors ➢NC and Nv are constant for a given material (effective mass) and temperature ➢Position of Fermi energy is important If EF is closer to EC than to Ev, n>p If EF is closer to Ev than to EC, n<p

The no and po Equations Charge Carriers in Semiconductors Q. 3 (From Q. 1) Calculate thermal equilibrium hole concentration in Si at T= 300 K. Assume that Fermi energy is 0. 25 e. V below the conduction band. The value of Nv for Si at T=300 K is 1. 04 x 1019 cm-3 and Eg = 1. 12 e. V.

The Intrinsic Carrier Concentration Charge Carriers in Semiconductors Intrinsic semiconductor; A pure semiconductor with no impurity atoms and no lattice defects in crystal 1. Carrier concentration(ni, pi) 2. Fermi energy, EF = intrinsic Fermi energy, EFi 1. Intrinsic carrier concentration Concentration of electron in in conduction band, ni Concentration of hole in in valence band, pi Independent of Fermi energy

The Intrinsic Carrier Concentration Charge Carriers in Semiconductors

The Intrinsic Carrier Concentration Charge Carriers in Semiconductors Q. 4; Given that the value of Nc and Nv for gallium arsenide (Ga. As) at 300 K are 4. 7 x 1017 cm-3 and 7. 0 x 1018 cm-3, respectively. Both Nc and Nv vary as T 3/2. Assume the bandgap energy of Ga. As is 1. 42 e. V and does not vary with temperature over this range, calculate the intrinsic carrier concentration in Ga. As at room temperature (T=300 K) and at T=450 K.

Charge Carriers in Semiconductors The Intrinsic Fermi-Level Position Intrinsic Fermi level position, EFi If EF closer to Ec, n>p If EF closer to Ev, n<p Intrinsic; n=p EF is located near the center of the forbidden bandgap Ec Emidgap Ev mp = mn EFi = Emidgap mp > mn EFi shifts slightly above the Emidgap mp > mn EFi shifts slightly below the Emidgap

The Intrinsic Fermi-Level Position Charge Carriers in Semiconductors

Dopant Atoms and Energy Levels Qualitative Description adding small, controlled amounts of specific dopant, or impurity, atoms Increase no. of carrier (either electron or hole) Alter the conductivity of semiconductor 3 valence 5 valence electrons III IV V B C Al Ga In Si Ge P As Sb Consider Phosphorus (P) and boron (B) as impurity atoms in Silicon (Si)

Qualitative Description Dopant Atoms and Energy Levels 1. P as substitutional impurity (group V element; 5 valence electron) Donor electron Ø In intrinsic Si, all 4 valence electrons contribute to covalent bonding. Ø In Si doped with P, 4 valence electron of P contribute to covalent bonding and 1 electron loosely bound to P atom (Donor electron). can easily break the bond and freely moves

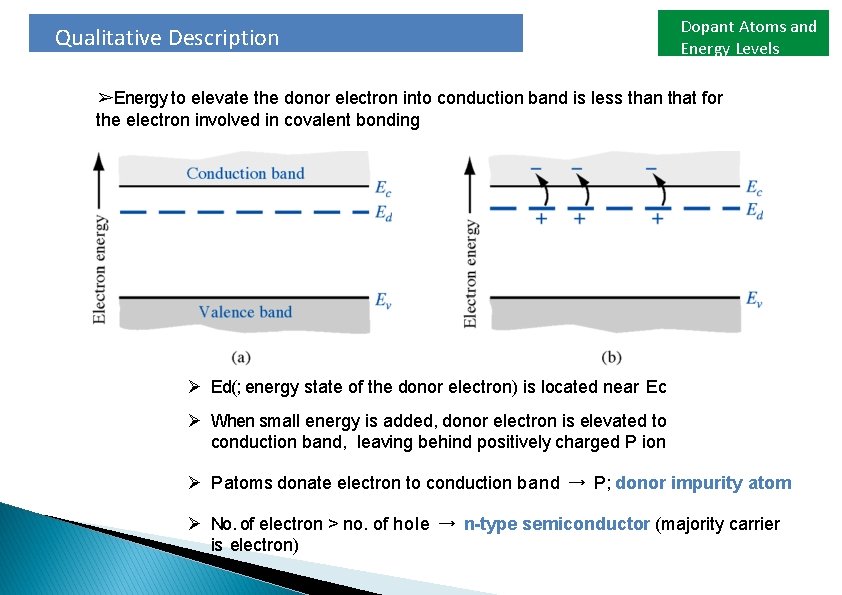
Qualitative Description Dopant Atoms and Energy Levels ➢Energy to elevate the donor electron into conduction band is less than that for the electron involved in covalent bonding Ø Ed(; energy state of the donor electron) is located near Ec Ø When small energy is added, donor electron is elevated to conduction band, leaving behind positively charged P ion Ø P atoms donate electron to conduction band → P; donor impurity atom Ø No. of electron > no. of hole → n-type semiconductor (majority carrier is electron)

Dopant Atoms and Energy Levels Qualitative Description 2. B as substitutional impurity (group III element; 3 valence electron) Ø In Si doped with B, all 3 valence electron of B contribute to covalent bonding and one covalent bonding is empty Ø When small energy is added, electron that involved in covalent bond will occupy the empty position leaving behind empty position that associated with Si atom Hole is created

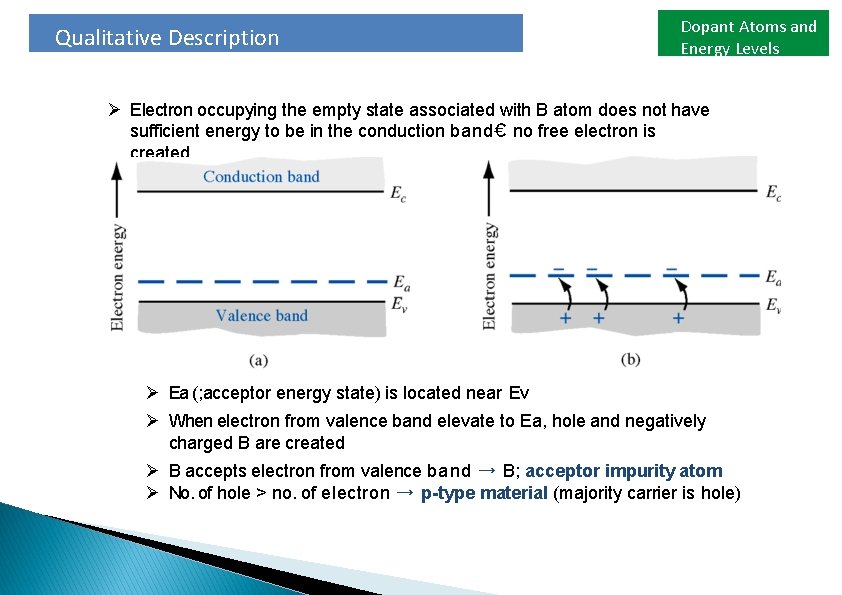
Qualitative Description Dopant Atoms and Energy Levels Ø Electron occupying the empty state associated with B atom does not have sufficient energy to be in the conduction band€ no free electron is created Ø Ea (; acceptor energy state) is located near Ev Ø When electron from valence band elevate to Ea, hole and negatively charged B are created Ø B accepts electron from valence band → B; acceptor impurity atom Ø No. of hole > no. of electron → p-type material (majority carrier is hole)

Dopant Atoms and Energy Levels Ionization Energy ➢Pure single-crystal semiconductor; intrinsic semiconductor ➢Semiconductor with dopant atoms; extrinsic semiconductor n-type Dopant atom; Majority carrier; ✓Donor impurity atom ✓electron p-type ✓Acceptor impurity atom ✓hole Ionization Energy The energy that required to elevate donor electron into the conduction (in case of donor impurity atom) or to elevate valence electron into acceptor state (in case of acceptor impurity atom).

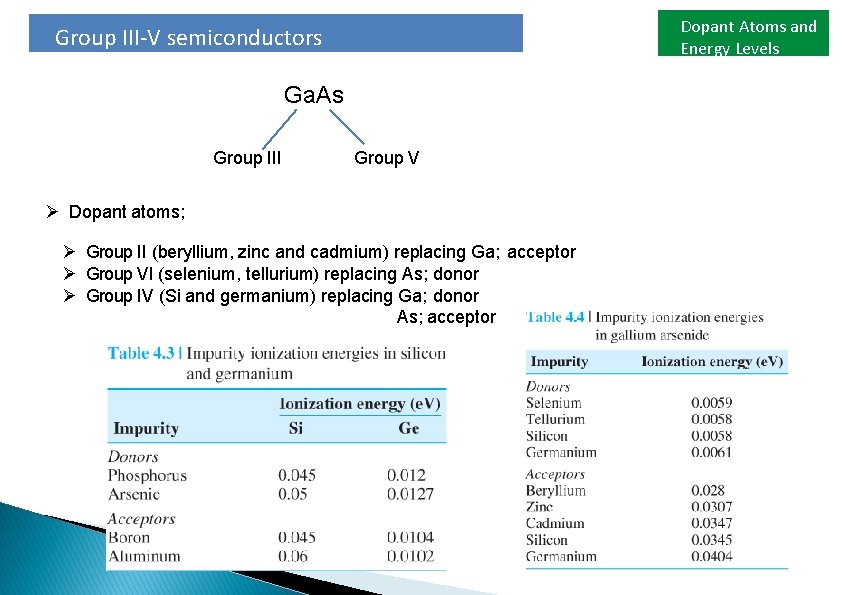
Dopant Atoms and Energy Levels Group III-V semiconductors Ga. As Group III Group V Ø Dopant atoms; Ø Group II (beryllium, zinc and cadmium) replacing Ga; acceptor Ø Group VI (selenium, tellurium) replacing As; donor Ø Group IV (Si and germanium) replacing Ga; donor As; acceptor

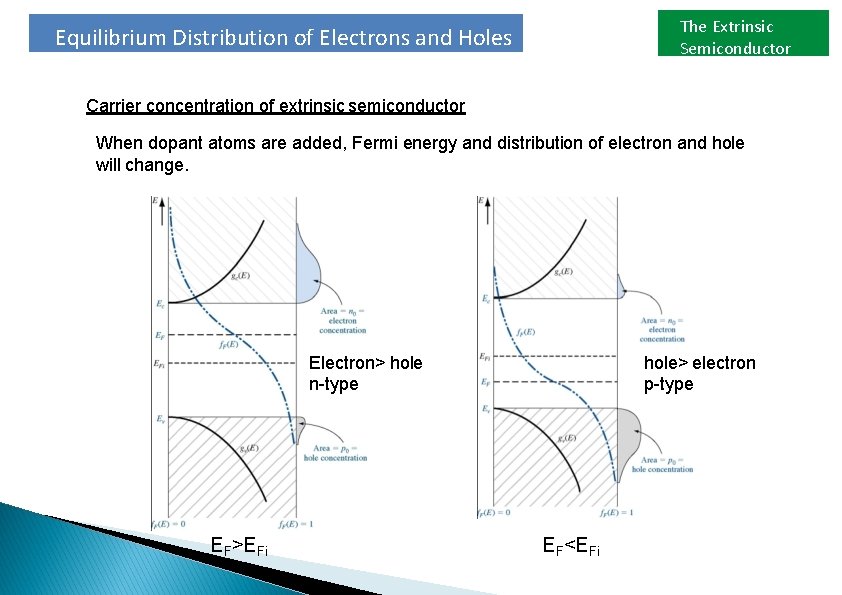
The Extrinsic Semiconductor Equilibrium Distribution of Electrons and Holes Carrier concentration of extrinsic semiconductor When dopant atoms are added, Fermi energy and distribution of electron and hole will change. Electron> hole n-type EF>EFi hole> electron p-type EF<EFi

Equilibrium Distribution of Electrons and Holes Thermal equilibrium concentration of electron Thermal equilibrium concentration of hole The Extrinsic Semiconductor

Equilibrium Distribution of Electrons and Holes The Extrinsic Semiconductor Q. 6; Calculate thermal equilibrium concentrations of electrons and holes for a given Fermi energy. Consider silicon at T = 300 K so that Nc = 2. 8 x 1019 cm-3 and Nv = 1. 04 x 1019 cm-3. Assume that the Fermi energy is 0. 25 e. V below the conduction band Eg = 1. 12 e. V.

The Product of no and po is always a constant for a given material at a given temperature. The Extrinsic Semiconductor

Degenerate and Nondegenerate Semiconductors The Extrinsic Semiconductor Nondegenerate Semiconductor Ø For cases that we assumed that electron/hole concentration is much lower than effective density of states in conduction band-NC /valence band -NV (or Fermi level is at least 3 k. T above Ev or 3 k. T below Ec) is referred as NONDEGENRATE SEMICONDUCTOR Ø COMPLETE IONIZATION : Enough thermal energy to supply the energy to ionize all donor impurities at room temperature and provide the same number of electrons in the conduction band. Electron Density under complete ionization: Fermi level : Concentration of holes under complete ionization: Fermi level : Higher donor/acceptor concentration- smaller ∆ E

Degenerate and Nondegenerate Semiconductors The Extrinsic Semiconductor Energy band of extrinsic semiconductors (a) donor ions, (b) acceptor ions Ø From Figure (a), the donor level ED is measured with respect to the bottom of the conduction band equal concentrations of electrons (which are mobile) and donor ions (which are immobile).

Degenerate and Nondegenerate Semiconductors Degenerate Semiconductor NA ≥ NV Or ND ≥ N C The Extrinsic Semiconductor

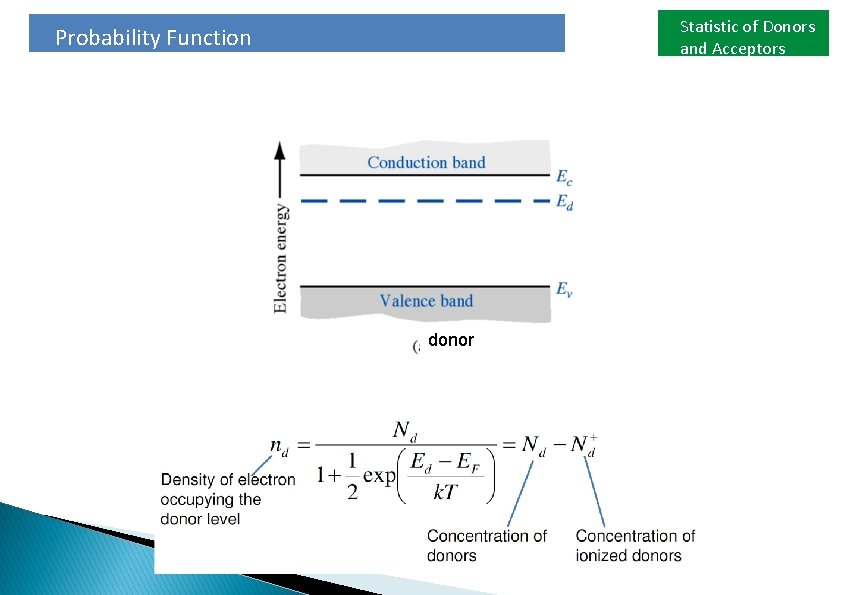
Statistic of Donors and Acceptors Probability Function Discrete donor level donor

Statistic of Donors and Acceptors Probability Function Discrete acceptor level acceptor

Statistic of Donors and Acceptors Probability Function from the probability function, we can calculate the friction of total electrons still in the donor states at T=300 K Ionization energy g = degeneracy factor, Si = 4

Probability Function Q. 7; Determine the fraction of total elements still in the donor states at T = 300 K. Consider phosphorus doping in Si for T=300 K at concentration of 1016 cm-3 (NC=2. 8 x 1019 cm-3, EC-Ed= 0. 045 e. V) Statistic of Donors and Acceptors

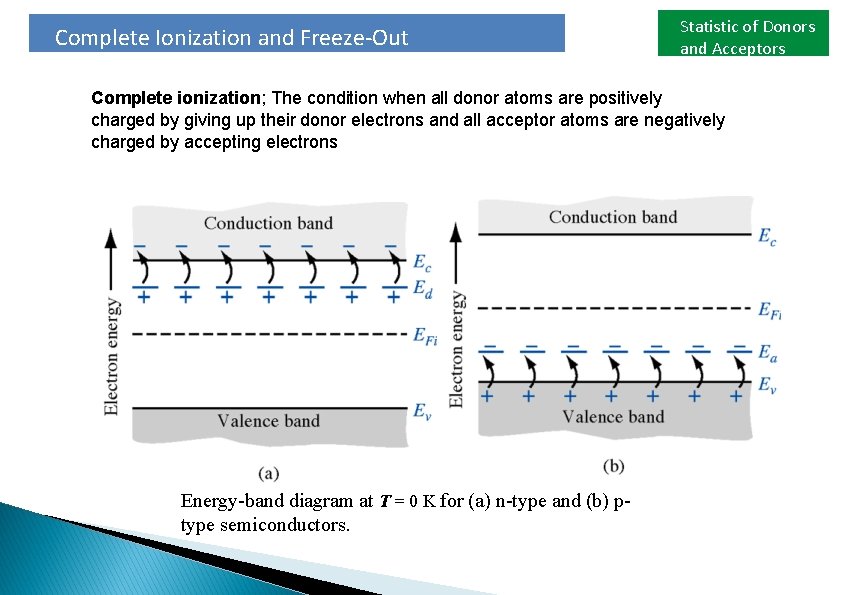
Complete Ionization and Freeze-Out Statistic of Donors and Acceptors Complete ionization; The condition when all donor atoms are positively charged by giving up their donor electrons and all acceptor atoms are negatively charged by accepting electrons Energy-band diagram at T = 0 K for (a) n-type and (b) ptype semiconductors.

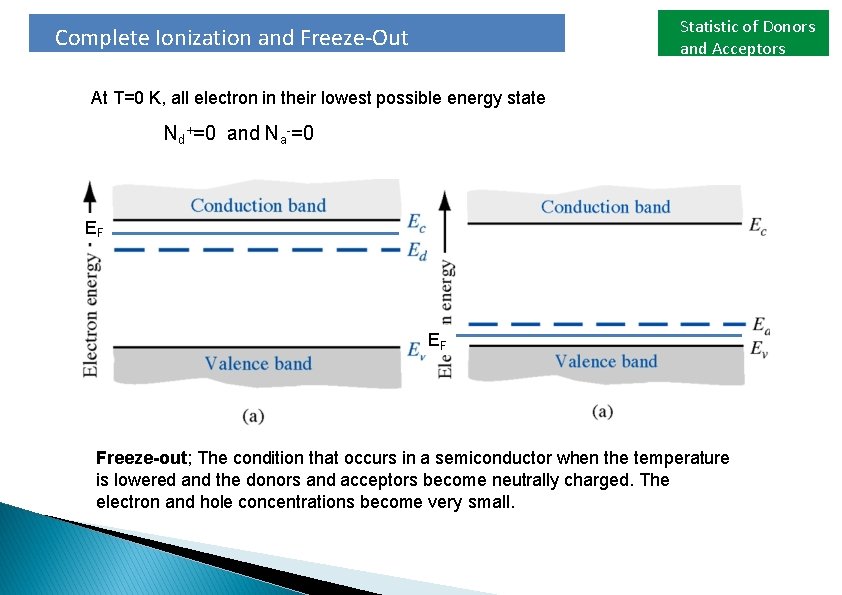
Statistic of Donors and Acceptors Complete Ionization and Freeze-Out At T=0 K, all electron in their lowest possible energy state Nd+=0 and Na-=0 EF EF Freeze-out; The condition that occurs in a semiconductor when the temperature is lowered and the donors and acceptors become neutrally charged. The electron and hole concentrations become very small.

Compensated Semiconductors Charge neutrality Charge-neutrality condition In thermal equilibrium, semiconductor crystal is electrically neutral “Negative charges = positive charge” Determined the carrier concentrations as a function of impurity doping concentration Compensated semiconductor; A semiconductor that contains both donor and acceptors at the same region If Nd > Na → n-type compensated semiconductor If Na > Nd → p-type compensated semiconductor If Nd = Na → has the characteristics of an intrinsic semiconductor

Compensated Semiconductors Charge neutrality Charge-neutrality condition Negative charges Positive charges no (N a pa ) po (N d nd )

Equilibrium Electron and Hole Concentrations Charge neutrality no (N a pa ) po (N d nd ) If we assume complete ionization (pa=0, nd=0) no Na po Nd Electron concentration is given as function of donors and acceptors concentrations

Equilibrium Electron and Hole Concentrations Charge neutrality Q 8; Consider an n-type silicon semiconductor at T=300 K in which Nd=1016 cm-3 and Na=0. The intrinsic carrier concentration is assumed to be ni=1. 5 x 1010 cm-3. Determine thermal equilibrium electron and hole concentrations.

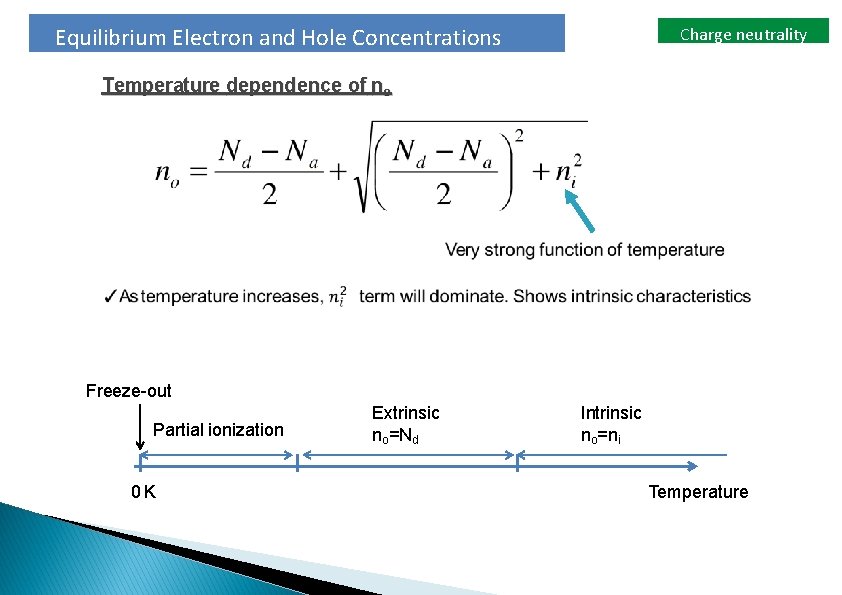
Equilibrium Electron and Hole Concentrations Charge neutrality Temperature dependence of no Freeze-out Partial ionization 0 K Extrinsic no=Nd Intrinsic no=ni Temperature

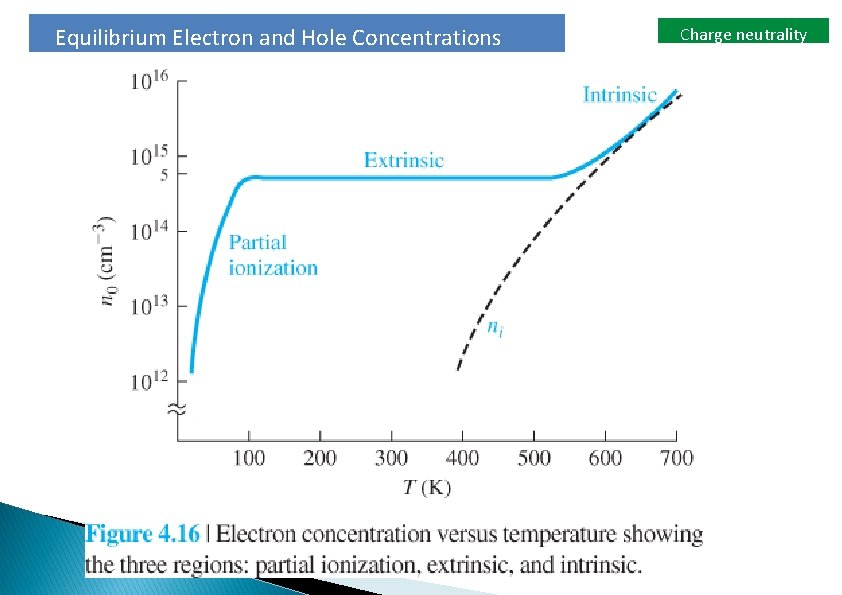
Equilibrium Electron and Hole Concentrations Charge neutrality

Equilibrium Electron and Hole Concentrations Hole concentration From charge-neutrality condition and nopo product no (N a pa ) po (N d nd ) no po n i 2 ni 2 po N a po N d Charge neutrality

Equilibrium Electron and Hole Concentrations Charge neutrality Q 9; Consider an p-type silicon semiconductor at T=300 K in which Na=1016 cm-3 and Nd=3 x 1015 cm-3. The intrinsic carrier concentration is assumed to be ni=1. 5 x 1010 cm-3. Determine thermal equilibrium electron and hole concentrations.

Mathematical Derivation As a function of doping concentration and temperature Equations for position of Fermi level (n-type) Position of Fermi Energy Level

Mathematical Derivation Equations for position of Fermi level (p-type) Position of Fermi Energy Level

Mathematical Derivation Position of Fermi Energy Level Q 10; Silicon at T=300 K contains an acceptor impurity concentration of Na=1016 cm-3. Determine the concentration of donor impurity atoms that must be added so that the Silicon is n-type and Fermi energy is 0. 20 e. V below the conduction band edge.

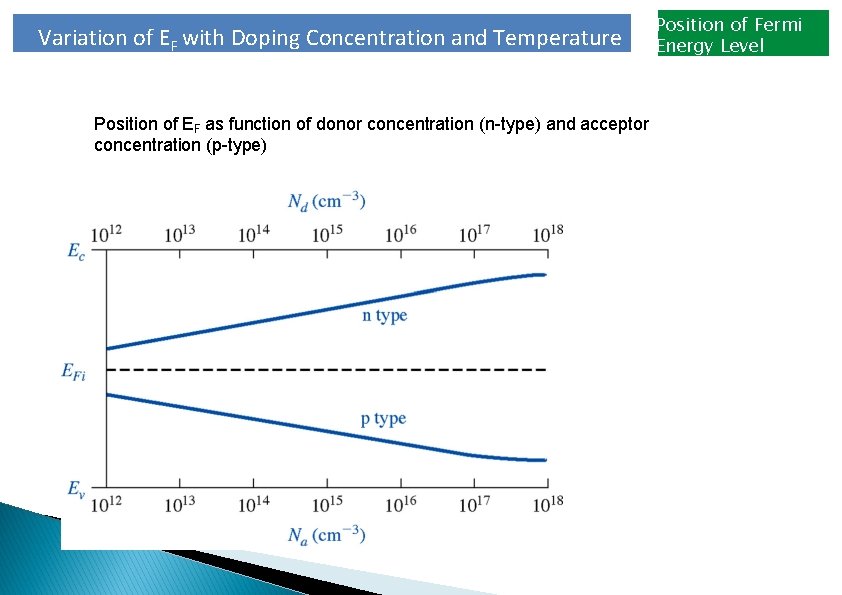
Variation of EF with Doping Concentration and Temperature Position of EF as function of donor concentration (n-type) and acceptor concentration (p-type) Position of Fermi Energy Level

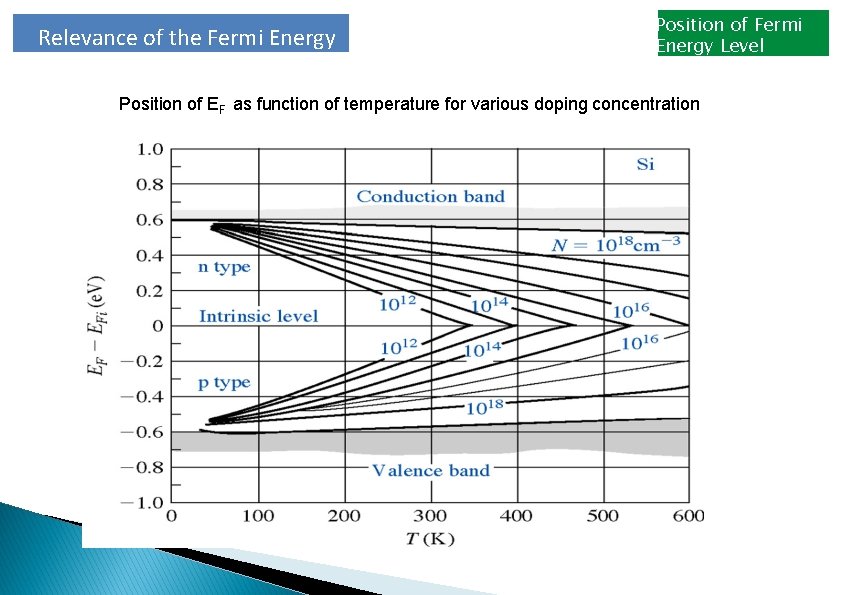
Relevance of the Fermi Energy Position of Fermi Energy Level Position of EF as function of temperature for various doping concentration

Summary Important terms Intrinsic semiconductor; A pure semiconductor material with no impurity atoms and no lattice defects in the crystal Extrinsic semiconductor; A semiconductor in which controlled amounts of donors and/or acceptors have been added so that the electron and hole concentrations change from the intrinsic carrier concentration and a preponderance of either electron (n-type) or hole (p-type) is created. Acceptor atoms; Impurity atoms added to a semiconductor to create a ptype material Donor atoms; Impurity atoms added to a semiconductor to create n-type material

Summary Complete ionization; The condition when all donor atoms are positively charged by giving up their donor electrons and all acceptor atoms are negatively charged by accepting electrons Freeze-out; The condition that occurs in a semiconductor when the temperature is lowered and the donors and acceptors become neutrally charged. The electron and hole concentrations become very small Fundamental relationship no po ni 2