EMT 125 3 DIGITAL ELECTRONIC PRINCIPLES 1 CHAPTER

EMT 125 /3 DIGITAL ELECTRONIC PRINCIPLES 1 CHAPTER 6 ADDERS Taught by: Jennifer Ong Siok Lan

Contents • • • Half Adder Full Adder 2 Bit Adder 3 Bit Adder 4 Bit Adder

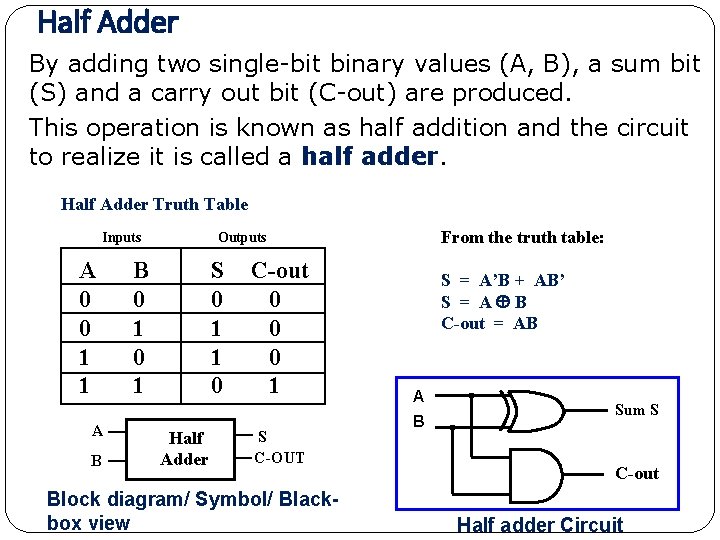
Half Adder By adding two single-bit binary values (A, B), a sum bit (S) and a carry out bit (C-out) are produced. This operation is known as half addition and the circuit to realize it is called a half adder. Half Adder Truth Table A 0 0 1 1 A B From the truth table: Outputs Inputs B 0 1 S 0 1 1 0 Half Adder C-out 0 0 0 1 S C-OUT Block diagram/ Symbol/ Blackbox view S = A’B + AB’ S = A B C-out = AB A B Sum S C-out Half adder Circuit

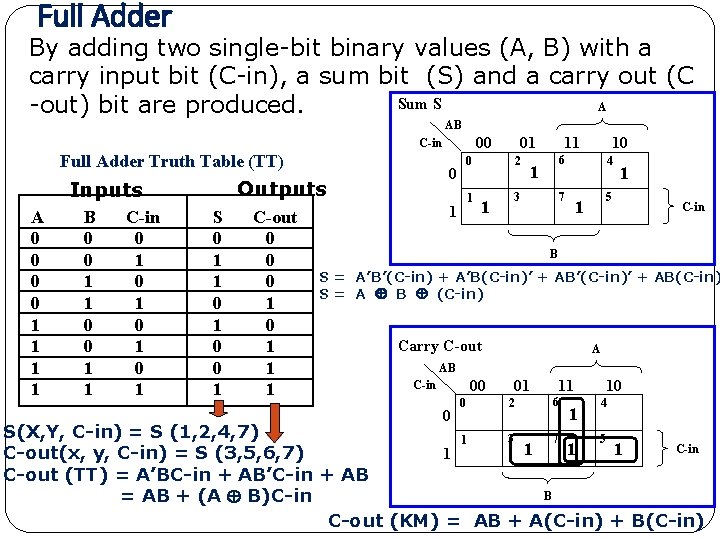
Full Adder By adding two single-bit binary values (A, B) with a carry input bit (C-in), a sum bit (S) and a carry out (C Sum S A -out) bit are produced. AB 00 C-in Full Adder Truth Table (TT) A 0 0 1 1 B 0 0 1 1 C-in 0 1 0 1 S 0 1 1 0 0 1 C-out 0 0 0 1 1 1 0 0 Outputs Inputs 01 1 1 2 1 11 10 6 1 3 4 7 1 5 1 C-in B S = A’B’(C-in) + A’B(C-in)’ + AB’(C-in)’ + AB(C-in) S = A B (C-in) Carry C-out A AB 00 C-in 0 0 01 2 11 6 1 10 4 S(X, Y, C-in) = S (1, 2, 4, 7) 3 5 7 1 C-in 1 1 C-out(x, y, C-in) = S (3, 5, 6, 7) C-out (TT) = A’BC-in + AB’C-in + AB B = AB + (A B)C-in C-out (KM) = AB + A(C-in) + B(C-in)

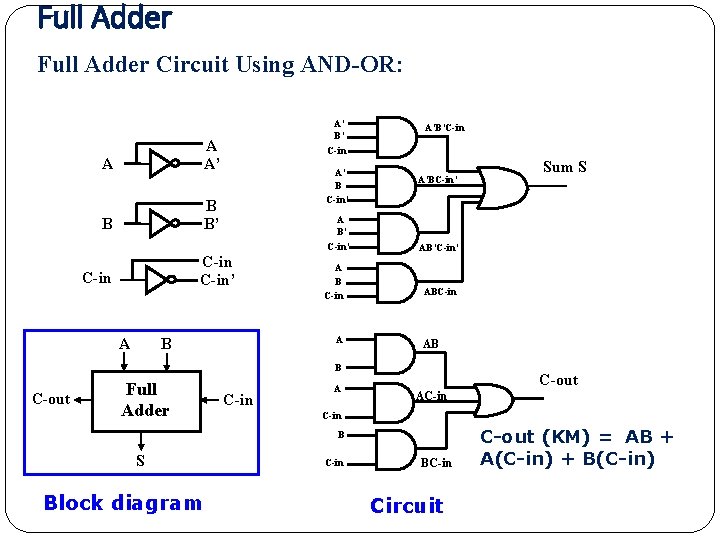
Full Adder Circuit Using AND-OR: A’ B’ C-in A A’ B C-in’ B B’ B A B’ C-in’ C-in A A B C-in A B A’B’C-in A’BC-in’ AB’C-in’ ABC-in AB B C-out Full Adder C-in A C-out AC-in B S Block diagram Sum S C-in BC-in Circuit C-out (KM) = AB + A(C-in) + B(C-in)

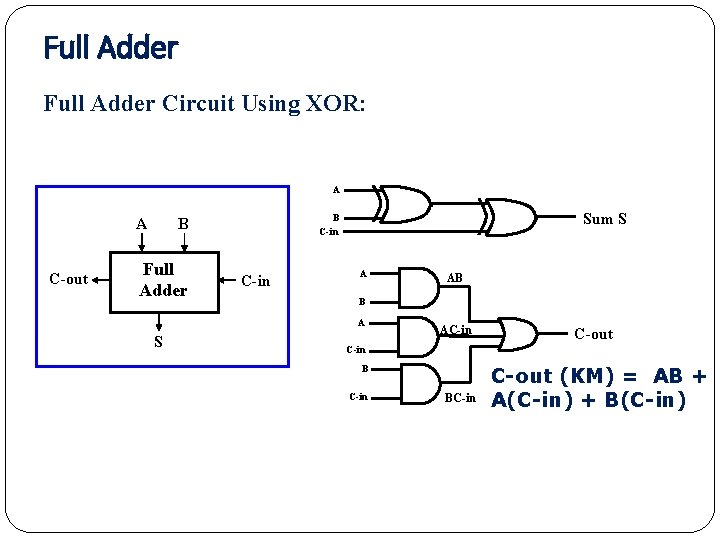
Full Adder Circuit Using XOR: A A C-out Full Adder Sum S B C-in A B A S AB AC-in C-out C-in BC-in C-out (KM) = AB + A(C-in) + B(C-in)

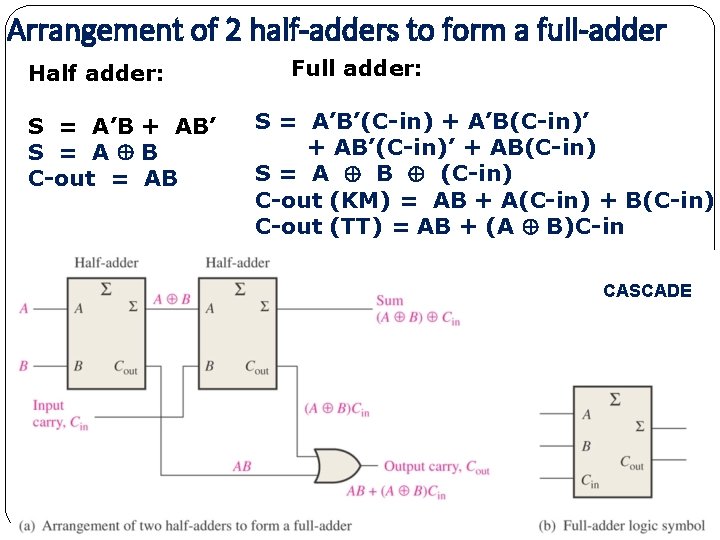
Arrangement of 2 half-adders to form a full-adder Half adder: S = A’B + AB’ S = A B C-out = AB Full adder: S = A’B’(C-in) + A’B(C-in)’ + AB’(C-in)’ + AB(C-in) S = A B (C-in) C-out (KM) = AB + A(C-in) + B(C-in) C-out (TT) = AB + (A B)C-in CASCADE

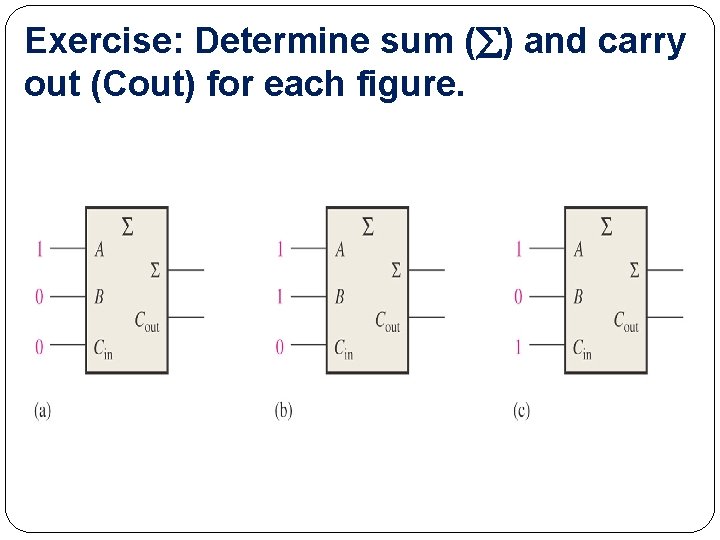
Exercise: Determine sum ( ) and carry out (Cout) for each figure.

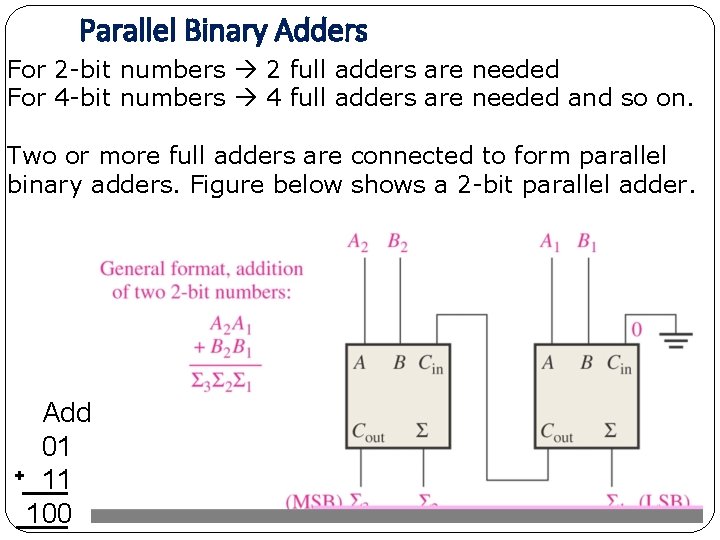
Parallel Binary Adders � A single full-adder is capable of adding two 1 -bit numbers and an input carry. � In order to add binary numbers with more than one bit, additional full adders must be used. � Consider the following case: 111 +01 100 � When one binary number is added to another, each column generates a sum bit and a 1 or 0 carry bit to the next column to the left.

Parallel Binary Adders For 2 -bit numbers 2 full adders are needed For 4 -bit numbers 4 full adders are needed and so on. Two or more full adders are connected to form parallel binary adders. Figure below shows a 2 -bit parallel adder. Add 01 + 11 100

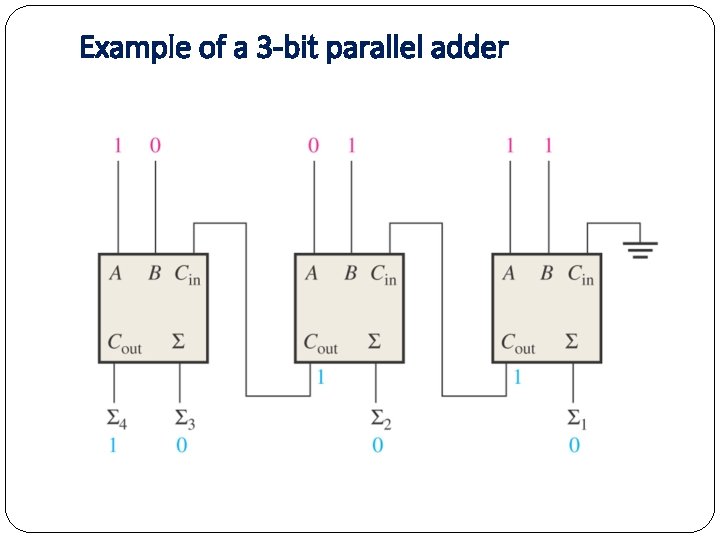
Example of a 3 -bit parallel adder

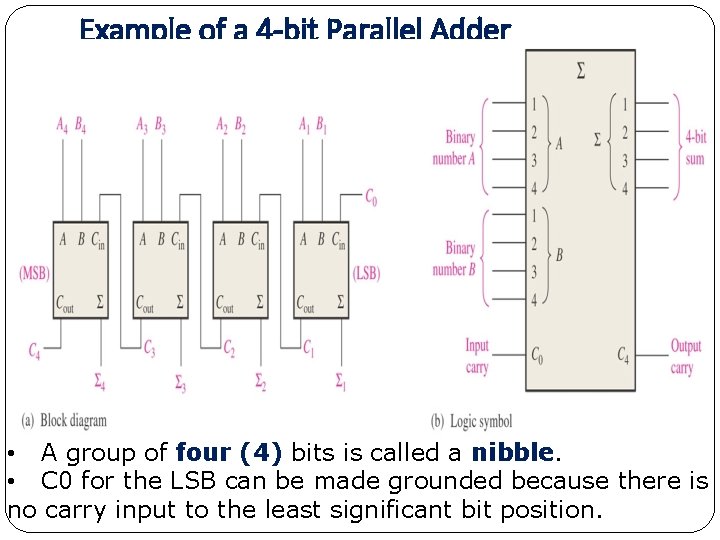
Example of a 4 -bit Parallel Adder • A group of four (4) bits is called a nibble. • C 0 for the LSB can be made grounded because there is no carry input to the least significant bit position.

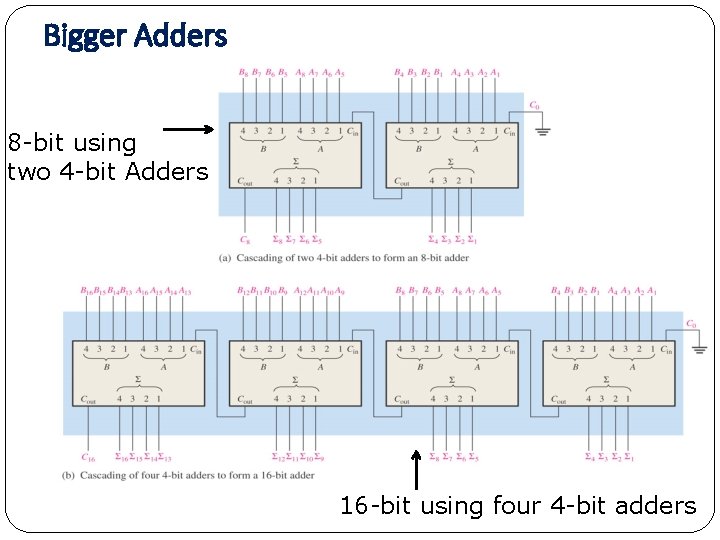
Bigger Adders 8 -bit using two 4 -bit Adders 16 -bit using four 4 -bit adders

Types of Parallel Adders 1) Ripple Carry Adder 2) Look-Ahead Carry Adder 3) Carry-Select Adder 4) Carry-Save Adder

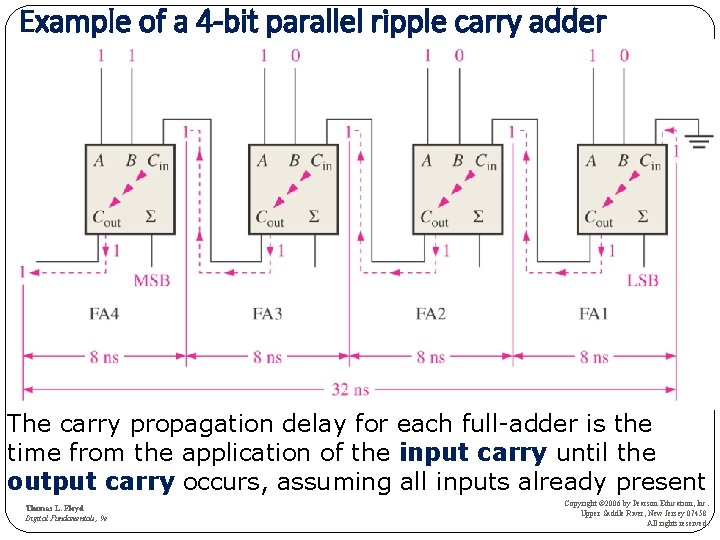
Ripple Carry Adder • The carry output of each full-adder is connected to the carry input of the next higher-order stage. • The sum and the output carry of any stage cannot be produced until the input carry occurs. • This causes delay in the addition process. • Consider an example of a 4 -bit full-adder given in the next slide.

Example of a 4 -bit parallel ripple carry adder The carry propagation delay for each full-adder is the time from the application of the input carry until the output carry occurs, assuming all inputs already present Thomas L. Floyd Digital Fundamentals, 9 e Copyright © 2006 by Pearson Education, Inc. Upper Saddle River, New Jersey 07458 All rights reserved.