Emittance Measurement for LCLS 13 December 2005 High

Emittance Measurement for LCLS 13 December 2005 High Level Applications Henrik Loos loos@slac. stanford. edu

Emittance Measurement Basics Measure different beam sizes “Three screen” At different locations (WS, OTR) with same accelerator setup “Quad scan” At same location (WS, OTR) with different accelerator setups Obtain transport (R)-Matrix from common starting point in accelerator for each measurement Least square fit for emittance Display results 13 December 2005 High Level Applications Henrik Loos loos@slac. stanford. edu

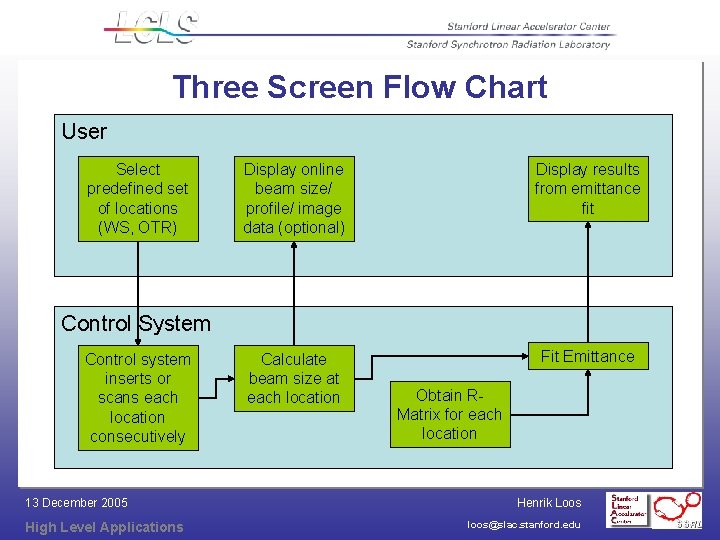
Three Screen Flow Chart User Select predefined set of locations (WS, OTR) Display online beam size/ profile/ image data (optional) Display results from emittance fit Calculate beam size at each location Fit Emittance Control System Control system inserts or scans each location consecutively 13 December 2005 High Level Applications Obtain RMatrix for each location Henrik Loos loos@slac. stanford. edu

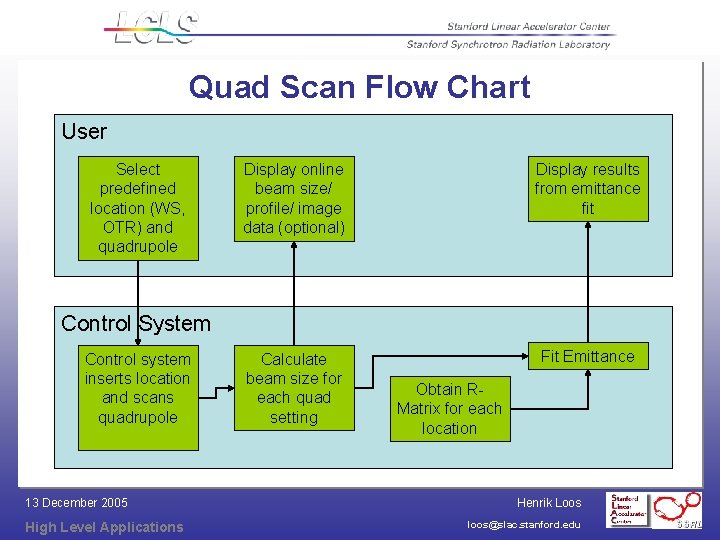
Quad Scan Flow Chart User Select predefined location (WS, OTR) and quadrupole Display online beam size/ profile/ image data (optional) Display results from emittance fit Calculate beam size for each quad setting Fit Emittance Control System Control system inserts location and scans quadrupole 13 December 2005 High Level Applications Obtain RMatrix for each location Henrik Loos loos@slac. stanford. edu

Software User front end Measurement sequence Beam data analysis R-Matrix generation Emittance calculation 13 December 2005 High Level Applications Henrik Loos loos@slac. stanford. edu

Emittance Algorithm Input List of beam sizes and their standard variations List of R-matrices corresponding to each measurement Output σ-matrix at start of beamline Twiss parameters, emittance Best fit beam sizes Standard deviations of all parameters 13 December 2005 High Level Applications Henrik Loos loos@slac. stanford. edu

Emittance Calculation Three independent values in σ-matrix, σ1, σ2, σ3 Related to measured beam size σx with R-matrix by σx 2 = R 112 σ1 + 2 R 11 R 12 σ2 + R 122 σ3 Form linear equations for measurement i: σx, i 2 = Σk. Mik σk Find σk by least squares fit Emittance is ε 2 = σ1 σ3 - σ22 Twiss parameters are β = σ1/ε, α = -σ2/ε Plus error calculation 13 December 2005 High Level Applications Henrik Loos loos@slac. stanford. edu