EMG Amplitude Estimation to Torque About a Joint

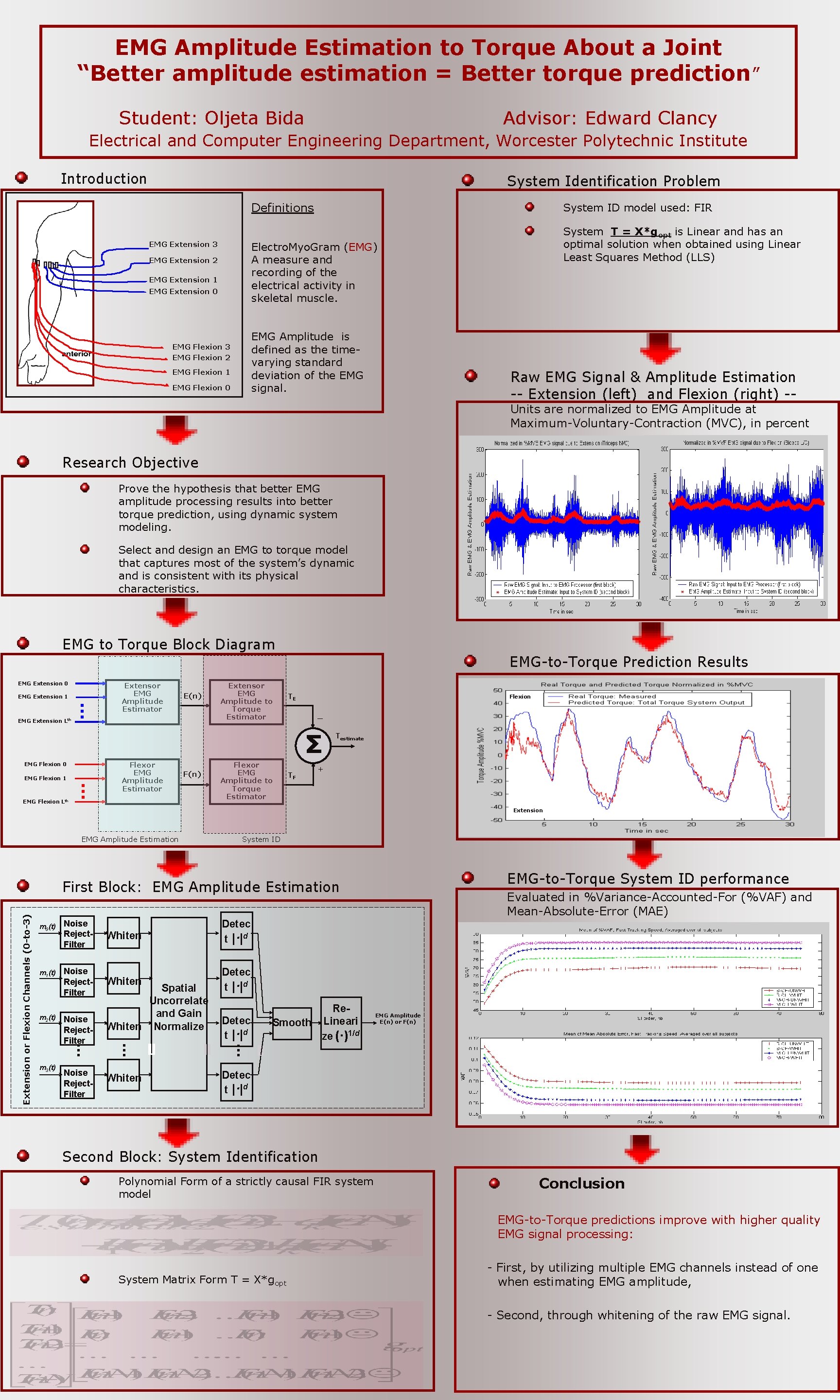
EMG Amplitude Estimation to Torque About a Joint “Better amplitude estimation = Better torque prediction” Student: Oljeta Bida Advisor: Edward Clancy Electrical and Computer Engineering Department, Worcester Polytechnic Institute Introduction System Identification Problem Definitions EMG Extension 3 System ID model used: FIR System T = X*gopt is Linear and has an optimal solution when obtained using Linear Least Squares Method (LLS) Electro. Myo. Gram (EMG) A measure and recording of the electrical activity in skeletal muscle. EMG Extension 2 EMG Extension 1 EMG Extension 0 EMG Amplitude is defined as the timevarying standard deviation of the EMG signal. EMG Flexion 3 EMG Flexion 2 EMG Flexion 1 EMG Flexion 0 Raw EMG Signal & Amplitude Estimation -- Extension (left) and Flexion (right) -- Units are normalized to EMG Amplitude at Maximum-Voluntary-Contraction (MVC), in percent Research Objective Prove the hypothesis that better EMG amplitude processing results into better torque prediction, using dynamic system modeling. Select and design an EMG to torque model that captures most of the system’s dynamic and is consistent with its physical characteristics. EMG to Torque Block Diagram EMG-to-Torque Prediction Results EMG Extension 0 EMG Extension 1 … EMG Extension Lth Extensor EMG Amplitude Estimator E(n) Extensor EMG Amplitude to Torque Estimator TE Flexion _ Σ EMG Flexion 0 EMG Flexion 1 … EMG Flexion Lth Flexor EMG Amplitude Estimator F(n) Flexor EMG Amplitude to Torque Estimator TF Testimate + Extension EMG Amplitude Estimation System ID EMG-to-Torque System ID performance Extension or Flexion Channels (0 -to-3) First Block: EMG Amplitude Estimation m 0(t) m 1(t) m 2(t) Noise Reject. Filter . . . m 3(t) Noise Reject. Filter Whiten Detec t |·|d Spatial Uncorrelate and Gain Whiten Normalize . . . Whiten Detec t |·|d . . . Re. Smooth Lineari ze (·)1/d Evaluated in %Variance-Accounted-For (%VAF) and Mean-Absolute-Error (MAE) EMG Amplitude E(n) or F(n) Detec t |·|d Second Block: System Identification Polynomial Form of a strictly causal FIR system model Conclusion EMG-to-Torque predictions improve with higher quality EMG signal processing: System Matrix Form T = X*gopt - First, by utilizing multiple EMG channels instead of one when estimating EMG amplitude, - Second, through whitening of the raw EMG signal.