Embedded Systems Design A Unified HardwareSoftware Introduction Chapter

Embedded Systems Design: A Unified Hardware/Software Introduction Chapter 2: Custom single-purpose processors 1

Outline • • • Introduction Combinational logic Sequential logic Custom single-purpose processor design RT-level custom single-purpose processor design Embedded Systems Design: A Unified Hardware/Software Introduction, (c) 2000 Vahid/Givargis 2

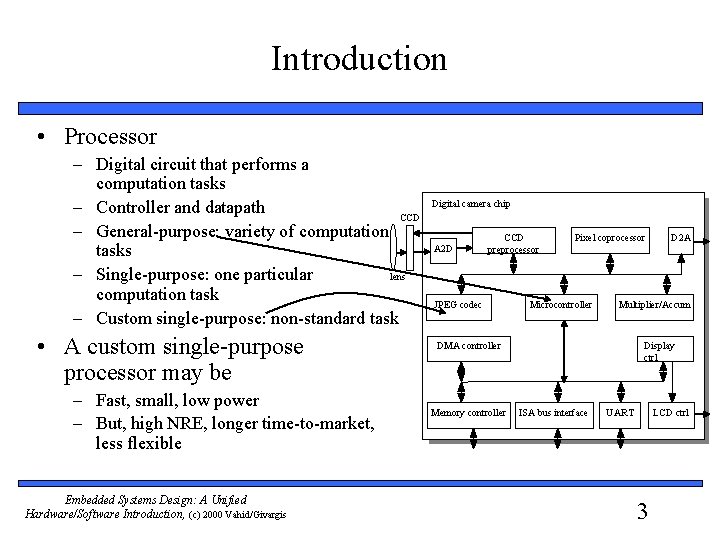
Introduction • Processor – Digital circuit that performs a computation tasks – Controller and datapath CCD – General-purpose: variety of computation tasks lens – Single-purpose: one particular computation task – Custom single-purpose: non-standard task • A custom single-purpose processor may be – Fast, small, low power – But, high NRE, longer time-to-market, less flexible Embedded Systems Design: A Unified Hardware/Software Introduction, (c) 2000 Vahid/Givargis Digital camera chip A 2 D CCD preprocessor JPEG codec Pixel coprocessor Microcontroller Multiplier/Accum DMA controller Memory controller D 2 A Display ctrl ISA bus interface UART LCD ctrl 3

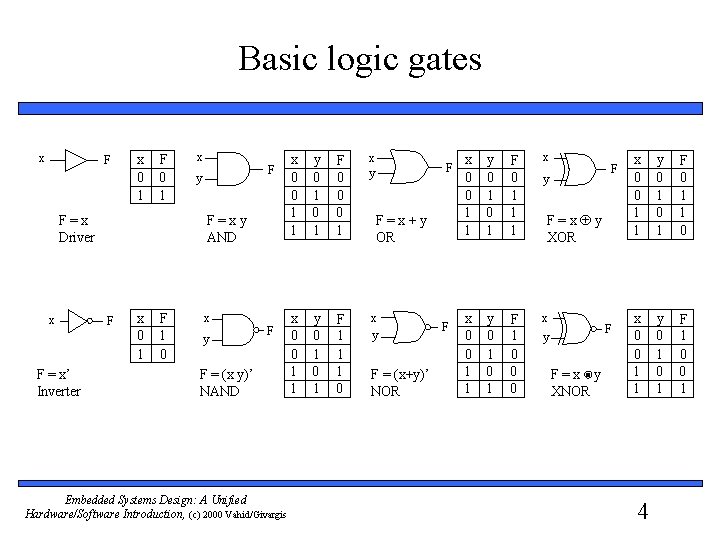
Basic logic gates x F x 0 1 F=x Driver x F = x’ Inverter x F y F=xy AND F x 0 1 F 1 0 x y F F = (x y)’ NAND Embedded Systems Design: A Unified Hardware/Software Introduction, (c) 2000 Vahid/Givargis x 0 0 1 1 y 0 1 F 0 0 0 1 x y x 0 0 1 1 y 0 1 F 1 1 1 0 x y F F=x+y OR F = (x+y)’ NOR F x 0 0 1 1 y 0 1 F 0 1 1 1 x x 0 0 1 1 y 0 1 F 1 0 0 0 x F y F=x y XOR F y F=x y XNOR x 0 0 1 1 y 0 1 F 0 1 1 0 x 0 0 1 1 y 0 1 F 1 0 0 1 4

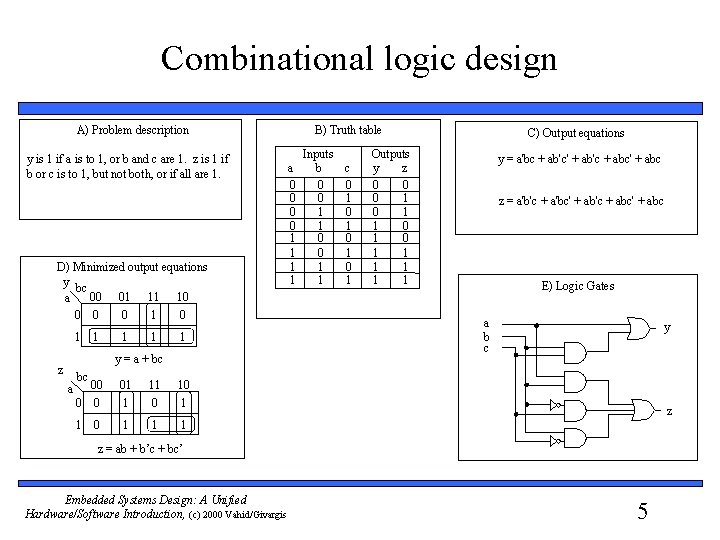
Combinational logic design B) Truth table A) Problem description y is 1 if a is to 1, or b and c are 1. z is 1 if b or c is to 1, but not both, or if all are 1. D) Minimized output equations y bc 00 01 11 10 a 0 0 0 1 1 1 y = a + bc z a bc 00 0 0 01 1 11 0 10 1 1 1 a 0 0 1 1 Inputs b c 0 0 0 1 1 C) Output equations Outputs y z 0 0 0 1 0 1 1 1 1 y = a'bc + ab'c' + ab'c + abc' + abc z = a'b'c + a'bc' + ab'c + abc' + abc E) Logic Gates a b c y z z = ab + b’c + bc’ Embedded Systems Design: A Unified Hardware/Software Introduction, (c) 2000 Vahid/Givargis 5

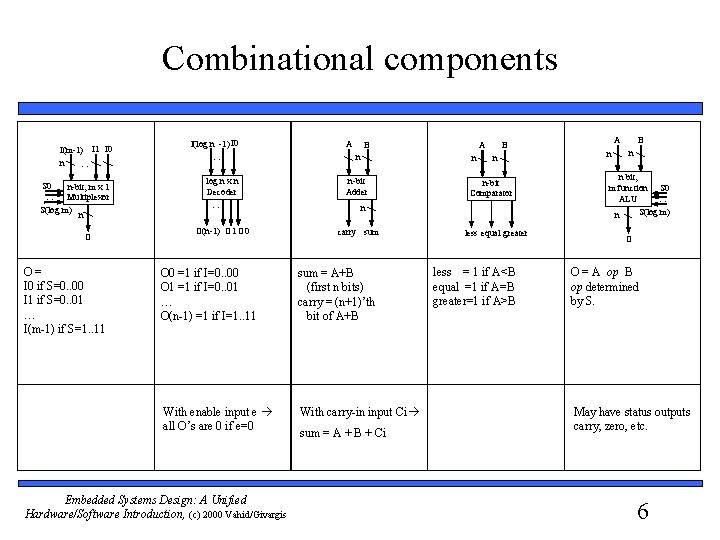
Combinational components I(m-1) I 1 I 0 n … S 0 … n-bit, m x 1 Multiplexor S(log m) n O O= I 0 if S=0. . 00 I 1 if S=0. . 01 … I(m-1) if S=1. . 11 I(log n -1) I 0 … A B n n log n x n Decoder … n-bit Adder O(n-1) O 1 O 0 carry sum B n n-bit Comparator n O 0 =1 if I=0. . 00 O 1 =1 if I=0. . 01 … O(n-1) =1 if I=1. . 11 sum = A+B (first n bits) carry = (n+1)’th bit of A+B With enable input e all O’s are 0 if e=0 With carry-in input Ci Embedded Systems Design: A Unified Hardware/Software Introduction, (c) 2000 Vahid/Givargis A sum = A + B + Ci less equal greater less = 1 if A<B equal =1 if A=B greater=1 if A>B A n B n n bit, m function S 0 ALU … S(log m) n O O = A op B op determined by S. May have status outputs carry, zero, etc. 6

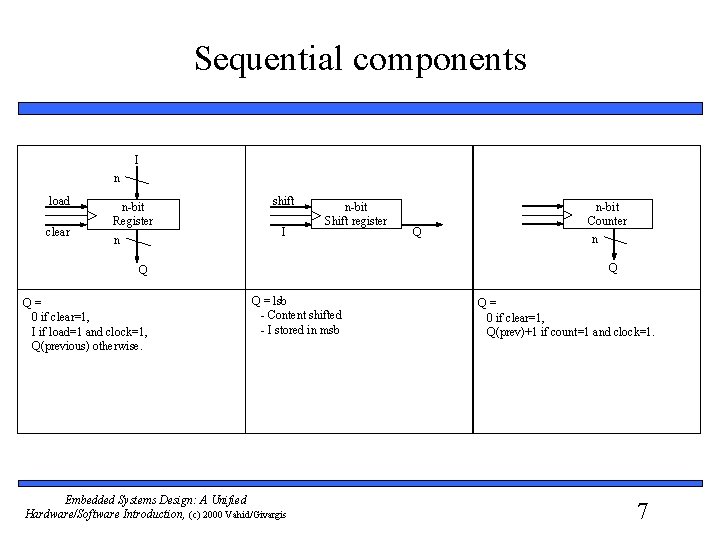
Sequential components I n load clear n-bit Register n shift I n-bit Shift register Q Q Q= 0 if clear=1, I if load=1 and clock=1, Q(previous) otherwise. Q n-bit Counter n Q = lsb - Content shifted - I stored in msb Embedded Systems Design: A Unified Hardware/Software Introduction, (c) 2000 Vahid/Givargis Q= 0 if clear=1, Q(prev)+1 if count=1 and clock=1. 7

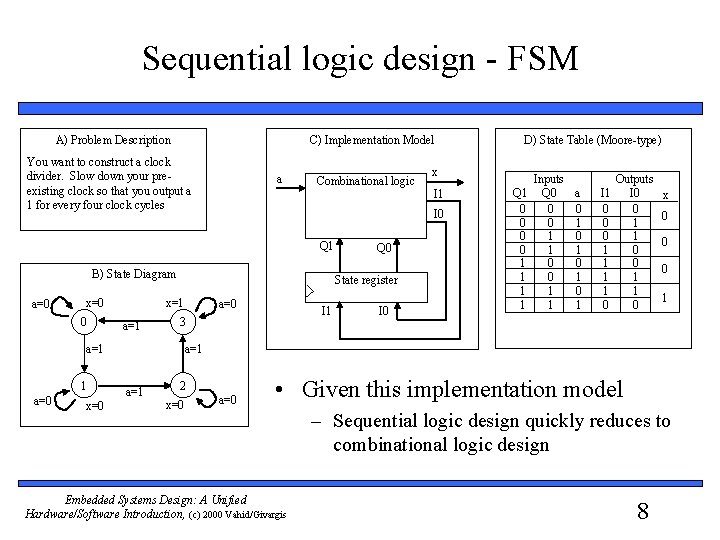
Sequential logic design - FSM C) Implementation Model A) Problem Description You want to construct a clock divider. Slow down your preexisting clock so that you output a 1 for every four clock cycles a Combinational logic B) State Diagram a=0 0 a=1 a=0 x=0 a=0 I 1 3 a=1 1 Q 0 State register x=1 x=0 x I 1 I 0 Q 1 I 0 D) State Table (Moore-type) Q 1 0 0 1 1 Inputs Q 0 a 0 0 0 1 1 I 1 0 0 0 1 1 0 Outputs I 0 0 1 1 0 x 0 0 0 1 a=1 2 x=0 a=0 • Given this implementation model Embedded Systems Design: A Unified Hardware/Software Introduction, (c) 2000 Vahid/Givargis – Sequential logic design quickly reduces to combinational logic design 8

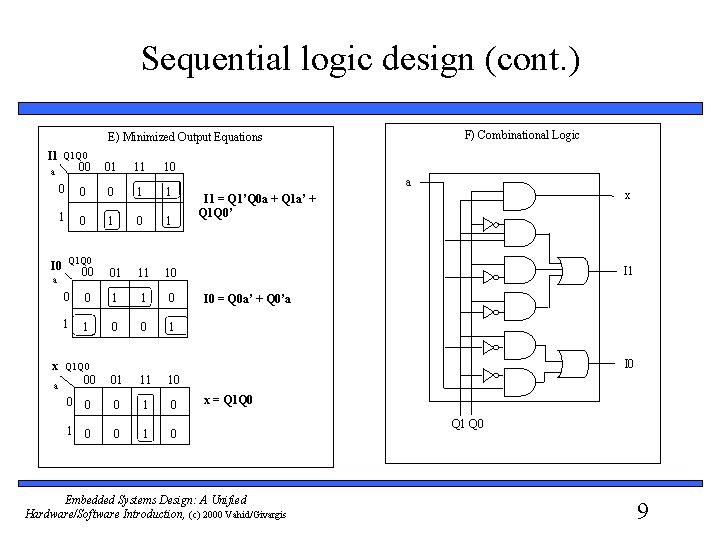
Sequential logic design (cont. ) F) Combinational Logic E) Minimized Output Equations I 1 Q 1 Q 0 00 a 01 11 10 0 1 1 1 0 1 01 11 10 I 0 Q 1 Q 0 00 a 0 0 1 1 0 0 1 x Q 1 Q 0 00 a a x I 1 = Q 1’Q 0 a + Q 1 a’ + Q 1 Q 0’ I 1 I 0 = Q 0 a’ + Q 0’a I 0 01 11 10 0 1 0 x = Q 1 Q 0 Embedded Systems Design: A Unified Hardware/Software Introduction, (c) 2000 Vahid/Givargis Q 1 Q 0 9

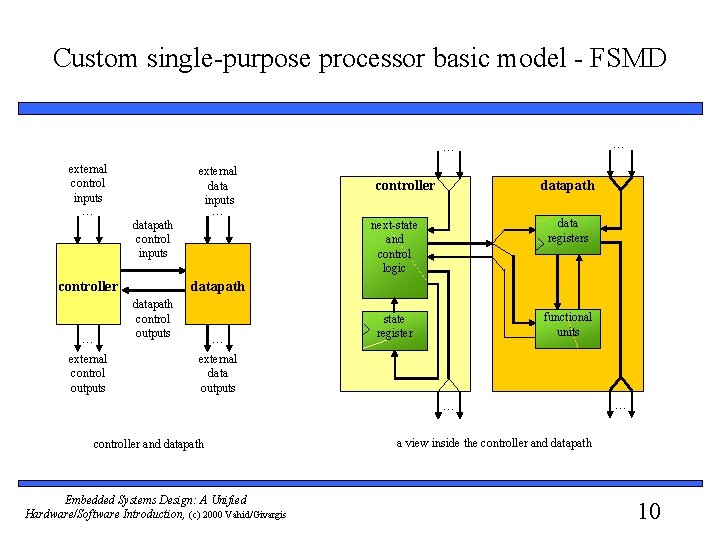
Custom single-purpose processor basic model - FSMD … … external control inputs … external data inputs … datapath control inputs controller … external control outputs controller datapath next-state and control logic data registers state register functional units datapath control outputs … external data outputs … controller and datapath Embedded Systems Design: A Unified Hardware/Software Introduction, (c) 2000 Vahid/Givargis … a view inside the controller and datapath 10

Register transfer level - RTL • O circuito digital é representado na forma: REG – L_COMB – REG ……. . • Os eventos num circuitos síncronos devem respeitar o período do Clock: 1) Leitura de Dados (após a borda ativa do Clock, respeitando tempo de Hold) 2) Processamento de Dados (Propagação dos dados através da L_COMB respeitando período do Clock e demais tempos) 3) Armazenamento de Dados (antes da próxima borda ativa do Clock, respeitando o tempo de Set-Up) Embedded Systems Design: A Unified Hardware/Software Introduction, (c) 2000 Vahid/Givargis 11

Example: greatest common divisor • First create algorithm • Convert algorithm to “complex” state machine – Known as FSMD: finitestate machine with datapath – Can use templates to perform such conversion Embedded Systems Design: A Unified Hardware/Software Introduction, (c) 2000 Vahid/Givargis (a) black-box view !1 1: 1 !(!go_i) (c) state diagram 2: go_i x_i y_i !go_i 2 -J: GCD d_o (b) desired functionality 0: int x, y; 1: while (1) { 2: while (!go_i); 3: x = x_i; 4: y = y_i; 5: while (x != y) { 6: if (x < y) 7: y = y - x; else 8: x = x - y; } 9: d_o = x; } 3: x = x_i 4: y = y_i !(x!=y) 5: x!=y 6: x<y 7: y = y -x !(x<y) 8: x = x - y 6 -J: 5 -J: 9: d_o = x 1 -J: 12

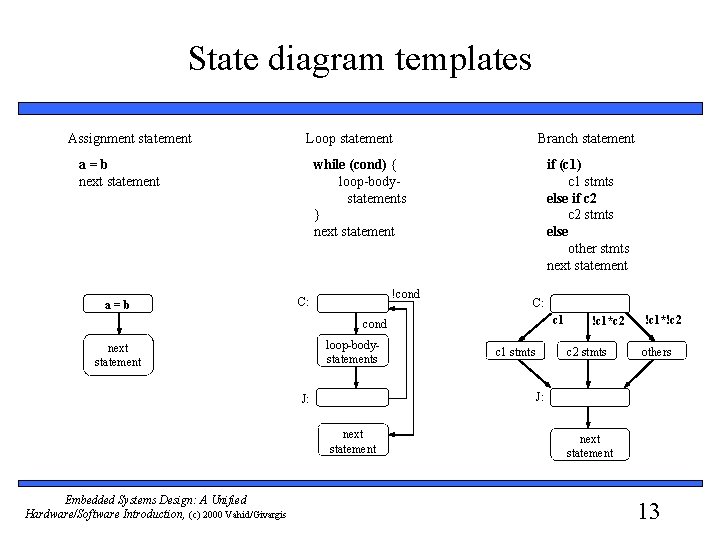
State diagram templates Assignment statement Loop statement a=b next statement a=b Branch statement while (cond) { loop-bodystatements } next statement !cond C: if (c 1) c 1 stmts else if c 2 stmts else other stmts next statement C: c 1 cond loop-bodystatements next statement c 2 stmts !c 1*!c 2 others J: next statement Embedded Systems Design: A Unified Hardware/Software Introduction, (c) 2000 Vahid/Givargis c 1 stmts !c 1*c 2 next statement 13

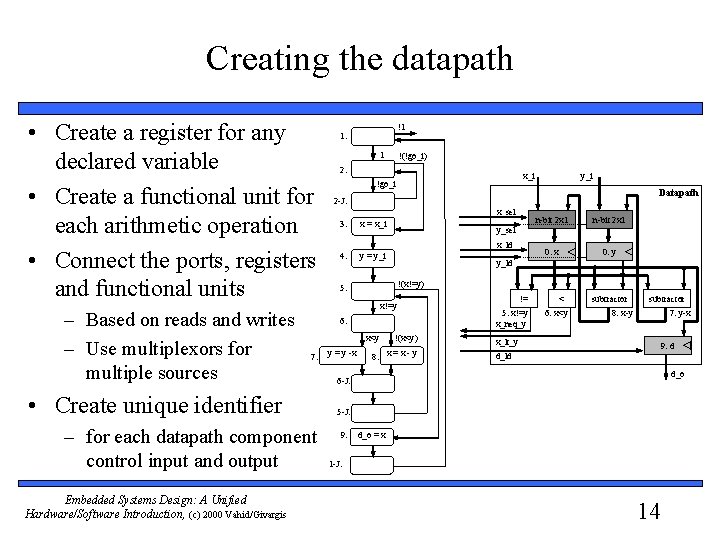
Creating the datapath • Create a register for any declared variable • Create a functional unit for each arithmetic operation • Connect the ports, registers and functional units – Based on reads and writes – Use multiplexors for multiple sources 1 !(!go_i) 2: x_i !go_i Datapath x_sel 3: x = x_i 4: y = y_i – for each datapath component control input and output n-bit 2 x 1 0: x 0: y y_ld !(x!=y) 5: x!=y y = y -x n-bit 2 x 1 y_sel x_ld x<y 7: y_i 2 -J: 6: • Create unique identifier Embedded Systems Design: A Unified Hardware/Software Introduction, (c) 2000 Vahid/Givargis !1 1: !(x<y) 8: x = x - y != 5: x!=y x_neq_y x_lt_y < 6: x<y subtractor 8: x-y 7: y-x 9: d d_ld d_o 6 -J: 5 -J: 9: d_o = x 1 -J: 14

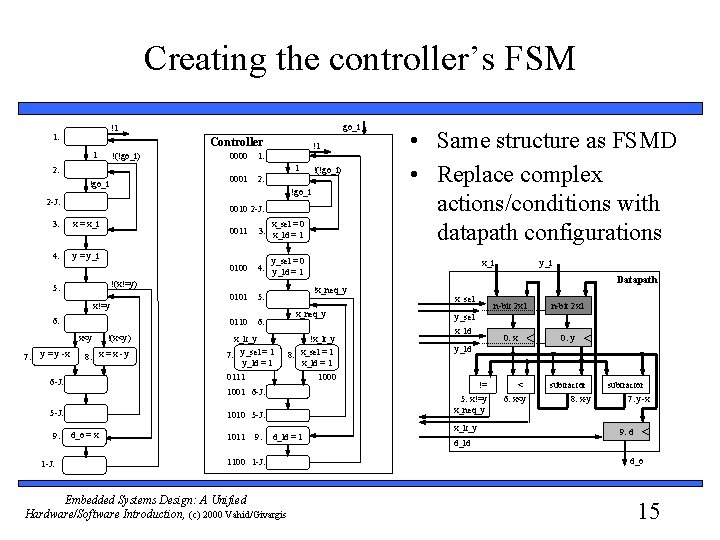
Creating the controller’s FSM Controller 1 !(!go_i) !go_i 1: 0001 2: !1 0010 2 -J: 3: x = x_i 4: y = y_i 0011 x_sel = 0 3: x_ld = 1 0100 y_sel = 0 4: y_ld = 1 !(x!=y) 5: x!=y 6: 0101 0110 x<y !(x<y) 8: x = x - y 5: x_lt_y 7: y_sel = 1 y_ld = 1 !x_lt_y x_sel =1 8: x_ld = 1 5 -J: 1011 9: d_ld = 1 1100 1 -J: Embedded Systems Design: A Unified Hardware/Software Introduction, (c) 2000 Vahid/Givargis n-bit 2 x 1 0: x 0: y y_sel x_ld y_ld != 5: x!=y x_neq_y 1010 5 -J: d_o = x x_sel 1000 1001 6 -J: y_i Datapath x_neq_y 6: • Same structure as FSMD • Replace complex actions/conditions with datapath configurations x_i !x_neq_y 0111 6 -J: 9: !(!go_i) !go_i 2 -J: y = y -x 0000 1 2: 7: go_i !1 1: x_lt_y < 6: x<y subtractor 8: x-y subtractor 7: y-x 9: d d_ld d_o 15

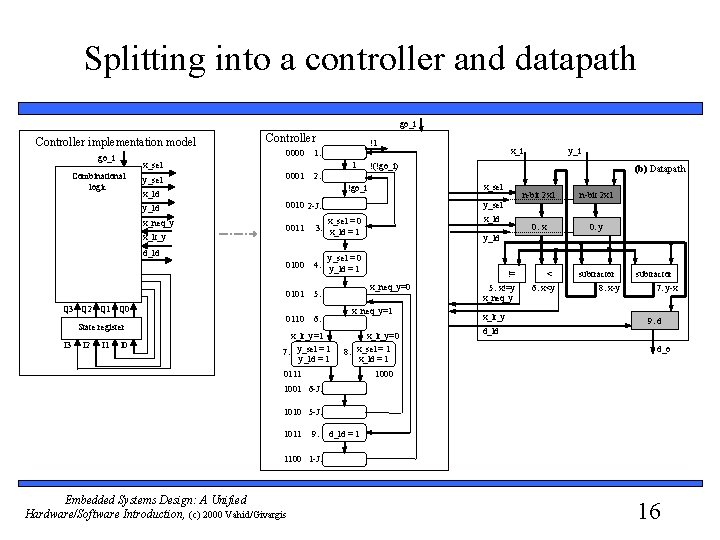
Splitting into a controller and datapath go_i Controller implementation model go_i Controller 0000 1 x_sel Combinational logic y_sel 0001 x_neq_y x_lt_y 0100 State register I 2 I 1 I 0 x_ld 0110 6: n-bit 2 x 1 0: x 0: y y_ld y_sel = 0 4: y_ld = 1 5: n-bit 2 x 1 y_sel x_sel = 0 3: x_ld = 1 0101 y_i (b) Datapath x_sel 0010 2 -J: 0011 x_i !(!go_i) !go_i d_ld Q 3 Q 2 Q 1 Q 0 2: x_ld y_ld I 3 !1 1: != x_neq_y=0 x_neq_y=1 x_lt_y=1 7: y_sel = 1 y_ld = 1 x_lt_y=0 x_sel =1 8: x_ld = 1 0111 5: x!=y x_neq_y x_lt_y < 6: x<y subtractor 8: x-y subtractor 7: y-x 9: d d_ld d_o 1000 1001 6 -J: 1010 5 -J: 1011 9: d_ld = 1 1100 1 -J: Embedded Systems Design: A Unified Hardware/Software Introduction, (c) 2000 Vahid/Givargis 16

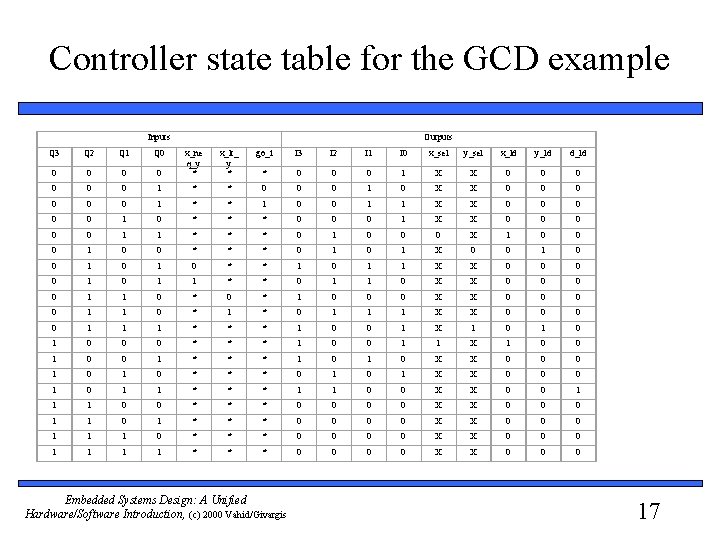
Controller state table for the GCD example Inputs Q 3 Q 2 Q 1 Q 0 0 0 0 Outputs x_lt_ y * go_i I 3 I 2 I 1 I 0 x_sel y_sel x_ld y_ld d_ld 0 x_ne q_y * * 0 0 0 1 X X 0 0 1 * * 0 0 0 1 0 X X 0 0 0 1 * * 1 0 0 1 1 X X 0 0 0 1 0 * * * 0 0 0 1 X X 0 0 0 1 1 * * * 0 1 0 0 0 X 1 0 0 0 1 0 0 * * * 0 1 X 0 0 1 0 1 0 * * 1 0 1 1 X X 0 0 1 0 1 1 * * 0 1 1 0 X X 0 0 1 1 0 * 1 0 0 0 X X 0 0 1 1 0 * 1 * 0 1 1 1 X X 0 0 1 1 1 * * * 1 0 0 1 X 1 0 1 0 0 0 * * * 1 0 0 1 1 X 1 0 0 1 * * * 1 0 X X 0 0 0 1 0 * * * 0 1 X X 0 0 0 1 1 * * * 1 1 0 0 X X 0 0 1 1 1 0 0 * * * 0 0 X X 0 0 0 1 1 0 1 * * * 0 0 X X 0 0 0 1 1 1 0 * * * 0 0 X X 0 0 0 1 1 * * * 0 0 X X 0 0 0 Embedded Systems Design: A Unified Hardware/Software Introduction, (c) 2000 Vahid/Givargis 17

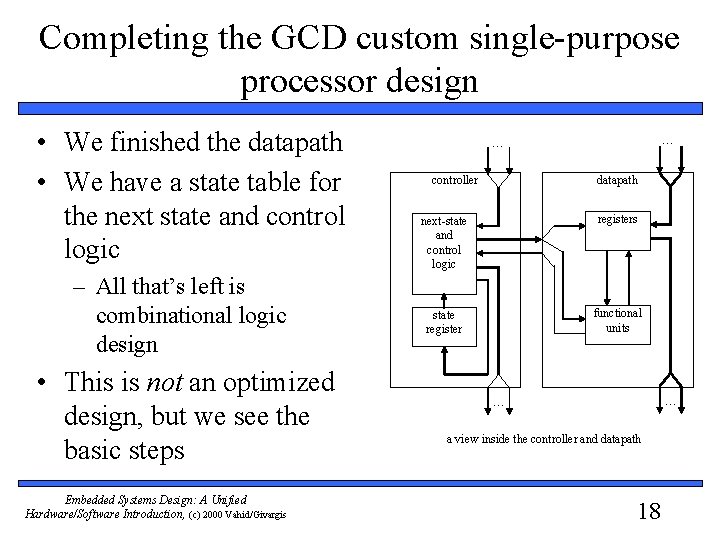
Completing the GCD custom single-purpose processor design • We finished the datapath • We have a state table for the next state and control logic – All that’s left is combinational logic design • This is not an optimized design, but we see the basic steps Embedded Systems Design: A Unified Hardware/Software Introduction, (c) 2000 Vahid/Givargis … … controller datapath next-state and control logic registers state register functional units … … a view inside the controller and datapath 18

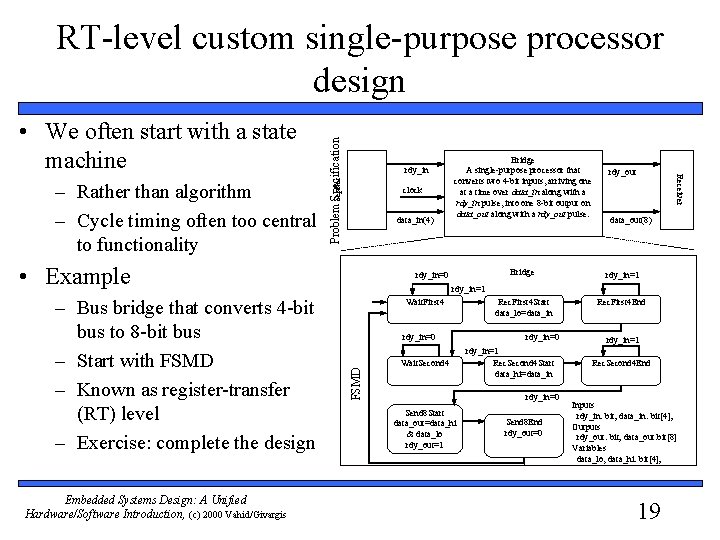
• We often start with a state machine rdy_in clock data_in(4) • Example Embedded Systems Design: A Unified Hardware/Software Introduction, (c) 2000 Vahid/Givargis rdy_in=0 rdy_out data_out(8) Bridge rdy_in=1 Rec. First 4 Start data_lo=data_in Rec. First 4 End rdy_in=1 Wait. First 4 rdy_in=0 FSMD – Bus bridge that converts 4 -bit bus to 8 -bit bus – Start with FSMD – Known as register-transfer (RT) level – Exercise: complete the design Bridge A single-purpose processor that converts two 4 -bit inputs, arriving one at a time over data_in along with a rdy_in pulse, into one 8 -bit output on data_out along with a rdy_out pulse. Receiver – Rather than algorithm – Cycle timing often too central to functionality Problem Sender Specification RT-level custom single-purpose processor design Wait. Second 4 rdy_in=0 rdy_in=1 Rec. Second 4 Start data_hi=data_in rdy_in=0 Send 8 Start data_out=data_hi & data_lo rdy_out=1 Send 8 End rdy_out=0 rdy_in=1 Rec. Second 4 End Inputs rdy_in: bit; data_in: bit[4]; Outputs rdy_out: bit; data_out: bit[8] Variables data_lo, data_hi: bit[4]; 19

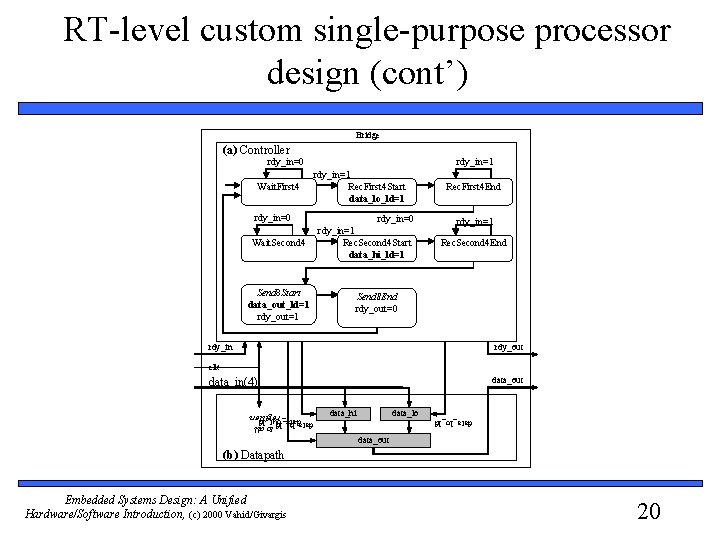
RT-level custom single-purpose processor design (cont’) Bridge (a) Controller rdy_in=0 Wait. First 4 rdy_in=0 Wait. Second 4 Send 8 Start data_out_ld=1 rdy_out=1 rdy_in=1 Rec. First 4 Start data_lo_ld=1 rdy_in=0 rdy_in=1 Rec. Second 4 Start data_hi_ld=1 Rec. First 4 End rdy_in=1 Rec. Second 4 End Send 8 End rdy_out=0 rdy_in rdy_out clk data_out data_in(4) data_hi data_lo_ld data_out to all data_hi_ld data_out_ld registers (b) Datapath Embedded Systems Design: A Unified Hardware/Software Introduction, (c) 2000 Vahid/Givargis 20

Optimizing single-purpose processors • Optimization is the task of making design metric values the best possible • Optimization opportunities – – original program FSMD datapath FSM Embedded Systems Design: A Unified Hardware/Software Introduction, (c) 2000 Vahid/Givargis 21

Optimizing the original program • Analyze program attributes and look for areas of possible improvement – – number of computations size of variable time and space complexity operations used • multiplication and division very expensive Embedded Systems Design: A Unified Hardware/Software Introduction, (c) 2000 Vahid/Givargis 22

Optimizing the original program (cont’) original program 0: int x, y; 1: while (1) { 2: while (!go_i); 3: x = x_i; 4: y = y_i; 5: while (x != y) { 6: if (x < y) 7: y = y - x; else 8: x = x - y; } 9: d_o = x; } replace the subtraction operation(s) with modulo operation in order to speed up program optimized program 0: int x, y, r; 1: while (1) { 2: while (!go_i); // x must be the larger number 3: if (x_i >= y_i) { 4: x=x_i; 5: y=y_i; } 6: else { 7: x=y_i; 8: y=x_i; } 9: while (y != 0) { 10: r = x % y; 11: x = y; 12: y = r; } 13: d_o = x; } GCD(42, 8) - 9 iterations to complete the loop GCD(42, 8) - 3 iterations to complete the loop x and y values evaluated as follows : (42, 8), (34, 8), (26, 8), (18, 8), (10, 8), (2, 6), (2, 4), (2, 2). x and y values evaluated as follows: (42, 8), (8, 2), (2, 0) Embedded Systems Design: A Unified Hardware/Software Introduction, (c) 2000 Vahid/Givargis 23

Optimizing the FSMD • Areas of possible improvements – merge states • states with constants on transitions can be eliminated, transition taken is already known • states with independent operations can be merged – separate states • states which require complex operations (a*b*c*d) can be broken into smaller states to reduce hardware size – scheduling Embedded Systems Design: A Unified Hardware/Software Introduction, (c) 2000 Vahid/Givargis 24

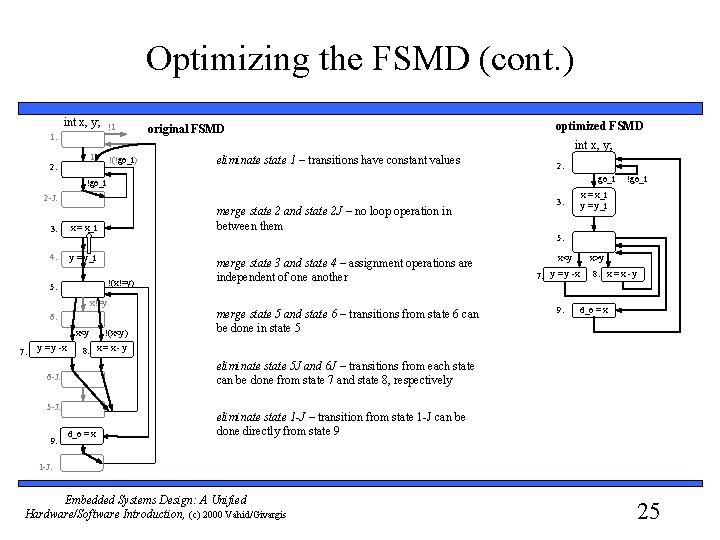
Optimizing the FSMD (cont. ) int x, y; !1 1: original FSMD optimized FSMD int x, y; 1 !(!go_i) 2: eliminate state 1 – transitions have constant values 2: go_i !go_i 2 -J: 3: x = x_i 4: y = y_i merge state 2 and state 2 J – no loop operation in between them !(x!=y) x!=y 6: x<y 7: !(x<y) merge state 3 and state 4 – assignment operations are independent of one another merge state 5 and state 6 – transitions from state 6 can be done in state 5 x<y 7: y = y -x 9: x>y 8: x = x - y d_o = x 8: x = x - y eliminate state 5 J and 6 J – transitions from each state can be done from state 7 and state 8, respectively 6 -J: 5 -J: 9: x = x_i y = y_i 5: y = y -x 3: !go_i d_o = x eliminate state 1 -J – transition from state 1 -J can be done directly from state 9 1 -J: Embedded Systems Design: A Unified Hardware/Software Introduction, (c) 2000 Vahid/Givargis 25

Optimizing the datapath • Sharing of functional units – one-to-one mapping, as done previously, is not necessary – if same operation occurs in different states, they can share a single functional unit • Multi-functional units – ALUs support a variety of operations, it can be shared among operations occurring in different states Embedded Systems Design: A Unified Hardware/Software Introduction, (c) 2000 Vahid/Givargis 26

Optimizing the FSM • State encoding – task of assigning a unique bit pattern to each state in an FSM – size of state register and combinational logic vary – can be treated as an ordering problem • State minimization – task of merging equivalent states into a single state • state equivalent if for all possible input combinations the two states generate the same outputs and transitions to the next same state Embedded Systems Design: A Unified Hardware/Software Introduction, (c) 2000 Vahid/Givargis 27

Summary • Custom single-purpose processors – – Straightforward design techniques Can be built to execute algorithms Typically start with FSMD CAD tools can be of great assistance Embedded Systems Design: A Unified Hardware/Software Introduction, (c) 2000 Vahid/Givargis 28