EM Waveguiding Overview Waveguide may refer to any

EM Waveguiding Overview • Waveguide may refer to any structure that conveys electromagnetic waves between its endpoints • Most common meaning is a hollow metal pipe used to carry radio waves • May be used to transport radiation of a single frequency • Transverse Electric (TE) modes have E ┴ kg (propagation wavevector) • Transverse Magnetic (TM) modes have B ┴ kg • Transverse Electric-Magnetic modes (TEM) have E, B ┴ kg • A cutoff frequency exists, below which no radiation propagates

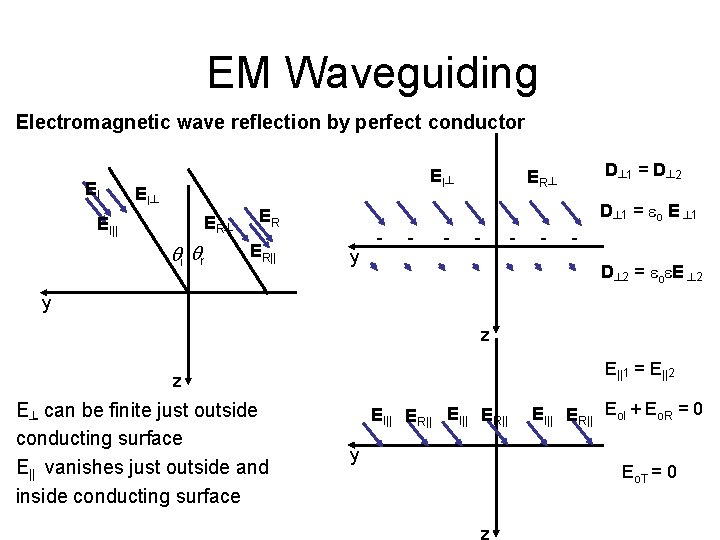
EM Waveguiding Electromagnetic wave reflection by perfect conductor EI EI┴ ER ┴ EI|| qi qr D┴ 1 = eo E ┴ 1 ER ER|| D┴ 1 = D┴ 2 ER ┴ y - - - D┴ 2 = eoe. E ┴ 2 y z E||1 = E||2 z E┴ can be finite just outside conducting surface E|| vanishes just outside and inside conducting surface EI|| ER|| y EI|| ER|| Eo. I + Eo. R = 0 Eo. T = 0 z

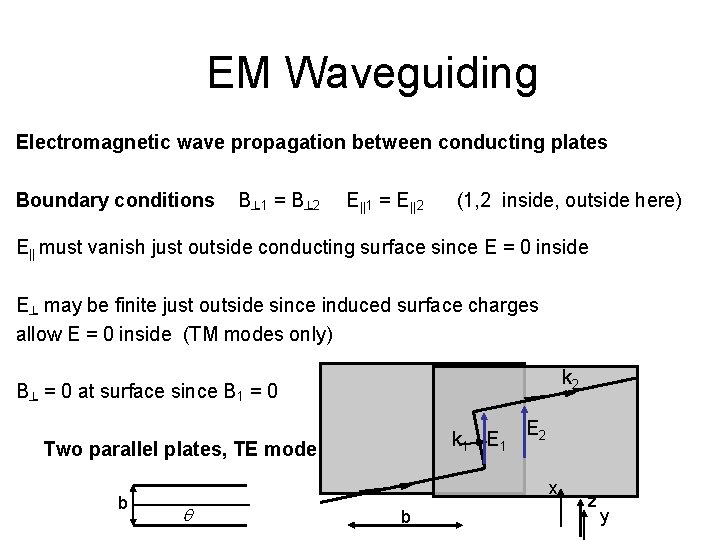
EM Waveguiding Electromagnetic wave propagation between conducting plates Boundary conditions B┴ 1 = B┴ 2 E||1 = E||2 (1, 2 inside, outside here) E|| must vanish just outside conducting surface since E = 0 inside E┴ may be finite just outside since induced surface charges allow E = 0 inside (TM modes only) k 2 B┴ = 0 at surface since B 1 = 0 k 1 E 1 Two parallel plates, TE mode b E 2 x q b z y

EM Waveguiding • Fields in vacuum E 1 = ex Eo ei(wt - k 1. r) k 1 = -ey k sinq + ez k cosq k 1. r = - ky sinq + kz cosq E 2 = -ex Eo ei(wt - k 2. r) k 2 = +ey k sinq + ez k cosq k 2. r = + ky sinq + kz cosq

EM Waveguiding • Fields E 1 = ex Eo ei(wt - k 1. r) k 1 = -ey k sinq + ez k cosq k 1. r = - ky sinq + kz cosq E 2 = -ex Eo ei(wt - k 2. r) k 2 = +ey k sinq + ez k cosq Ex k 2. r = + ky sinq + kz cosq sin(npy/b) y

EM Waveguiding •

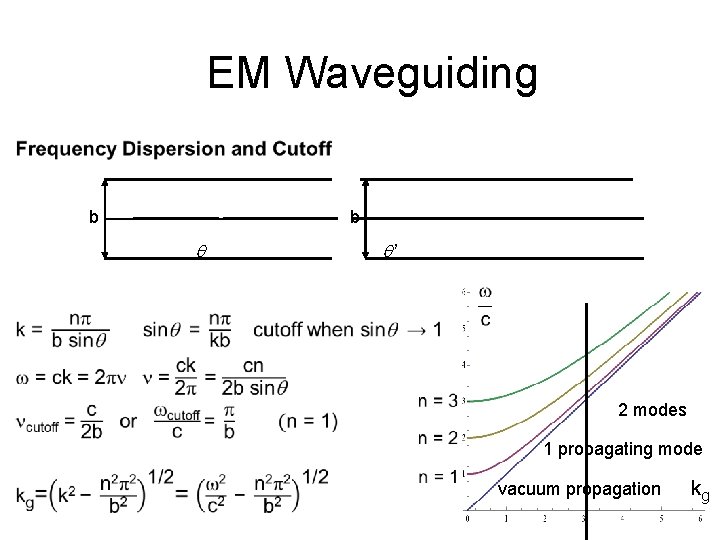
EM Waveguiding • b b q q’ 2 modes 1 propagating mode vacuum propagation kg

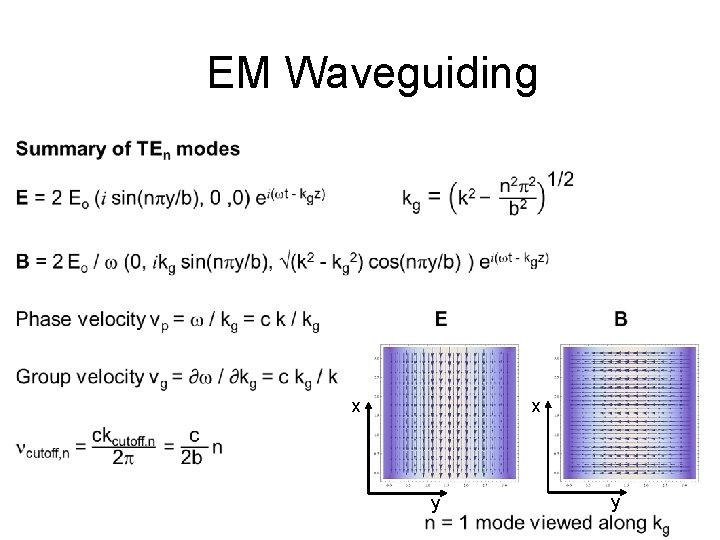
EM Waveguiding • x x y y

EM Waveguiding Electric components of TEn guided fields viewed along x (plan view) n=1 n=2 n=3 n=4 z y Magnetic components of TEn guided fields viewed along x (plan view) z y

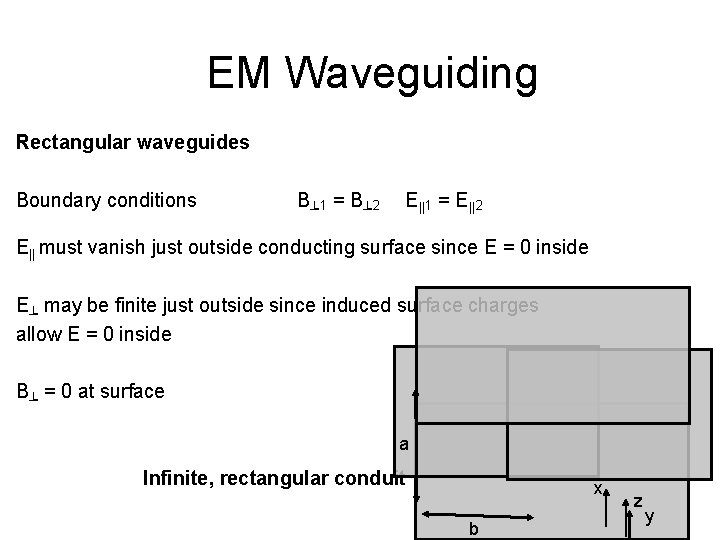
EM Waveguiding Rectangular waveguides Boundary conditions B┴ 1 = B┴ 2 E||1 = E||2 E|| must vanish just outside conducting surface since E = 0 inside E┴ may be finite just outside since induced surface charges allow E = 0 inside B┴ = 0 at surface a 0 Infinite, rectangular conduit b x z y

EM Waveguiding TEmn modes in rectangular waveguides TEn modes for two infinite plates are also solutions for the rectangular guide E field vanishes on xz plane plates as before, but not on the yz plane plates Charges are induced on the yz plates such that E = 0 inside the conductors Let Ex = C f(x) sin(npy/b) ei(wt - kgz) In free space . E = 0 and Ez = 0 for a TEmn mode and ∂Ez/∂z = 0 Hence ∂Ex/∂x = -∂Ey/∂y f(x) = -np / b cos(mpx/a) satisfies this condition By integration Ex = -C np / b cos(mpx/a) sin(npy/b) ei(wt - kgz) Ey = C mp / a sin(mpx/a) cos(npy/b) ei(wt - kgz) Ez = 0

EM Waveguiding •

EM Waveguiding •

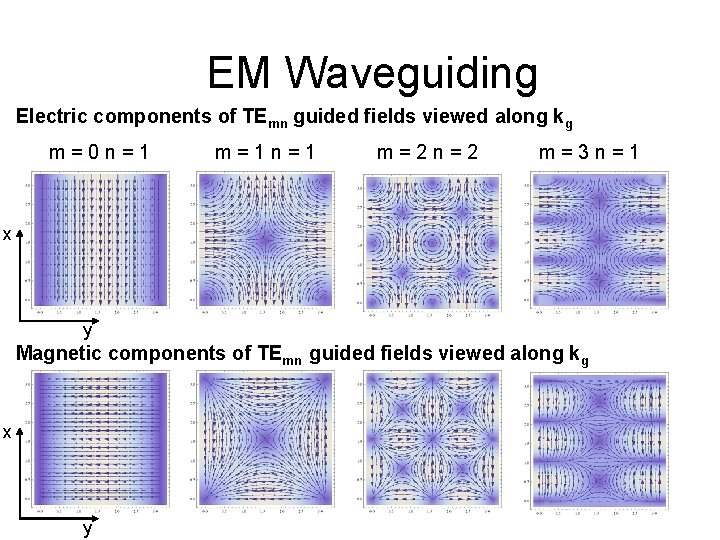
EM Waveguiding Electric components of TEmn guided fields viewed along kg m=0 n=1 m=1 n=1 m=2 n=2 m=3 n=1 x y Magnetic components of TEmn guided fields viewed along kg x y

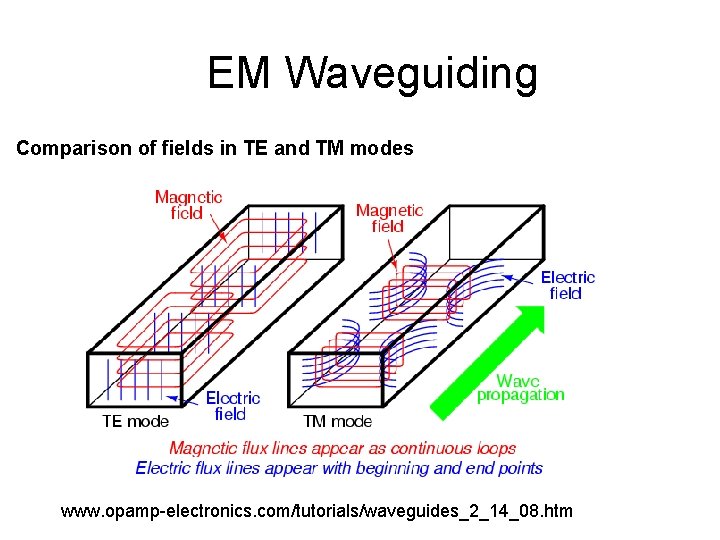
EM Waveguiding Comparison of fields in TE and TM modes www. opamp-electronics. com/tutorials/waveguides_2_14_08. htm

EM Waveguiding •