EM Algorithm with Markov Chain Monte Carlo Method

EM Algorithm with Markov Chain Monte Carlo Method for Bayesian Image Analysis Kazuyuki Tanaka Graduate School of Information Sciences, Tohoku University http: //www. smapip. is. tohoku. ac. jp/~kazu/ Collaborators: D. M. Titterington (Department of Statistics, University of Glasgow) 10 October, 2007 University of Glasgow 1

Contents 1. 2. 3. 4. Introduction Gaussian Graphical Model and EM Algorithm Markov Chain Monte Carlo Method Concluding Remarks 10 October, 2007 University of Glasgow 2

Contents 1. 2. 3. 4. Introduction Gaussian Graphical Model and EM Algorithm Markov Chain Monte Carlo Method Concluding Remarks 10 October, 2007 University of Glasgow 3

MRF and Statistical Inference Geman and Geman (1986): IEEE Transactions on PAMI Image Processing for Markov Random Fields (MRF) (Simulated Annealing, Line Fields) How can we estimate hyperparameters in the degradation process and in the prior model only from observed data? • EM Algorithm In the EM algorithm, we have to calculate some statistical quantities in the posterior and the prior models. • Belief Propagation • Markov Chain Monte Carlo Method 10 October, 2007 University of Glasgow 4

Statistical Analysis in EM Algorithm K. Tanaka, H. Shouno, M. Okada and D. M. Titterington: J. Phys. A 2004 Hyperparameter Estimation by using Belief Propagation (BP) for Gaussian Graphical Model in Image Processing J. Inoue and K. Tanaka: Phys. Rev. E 2002, J. Phys. A 2003 Statistical Behaviour of EM Algorithm for MRF (Graphical Models on Complete Graph) It is possible to estimate statistical behaviour of EM algorithm with belief propagation analytically. K. Tanaka and D. M. Titterington: J. Phys. A 2007 Statistical Trajectory of Approximate EM Algorithm for Probabilistic Image Processing 10 October, 2007 University of Glasgow 5

Contents 1. 2. 3. 4. Introduction Gaussian Graphical Model and EM Algorithm Markov Chain Monte Carlo Method Concluding Remarks 10 October, 2007 University of Glasgow 6

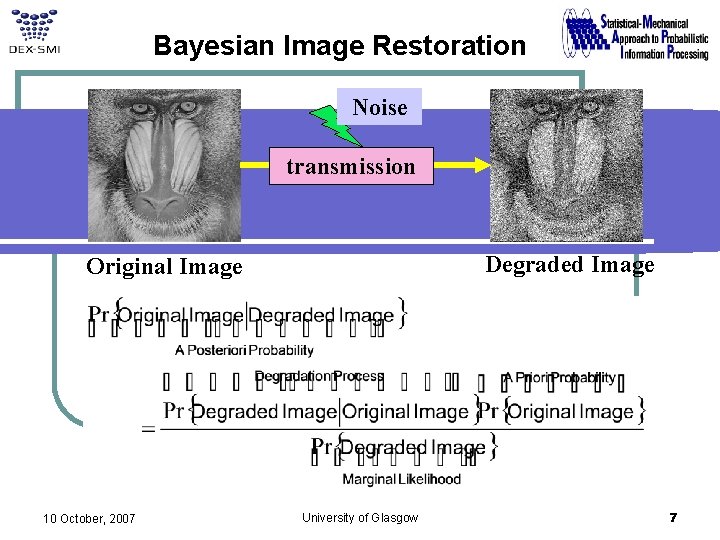
Bayesian Image Restoration Noise transmission Degraded Image Original Image 10 October, 2007 University of Glasgow 7

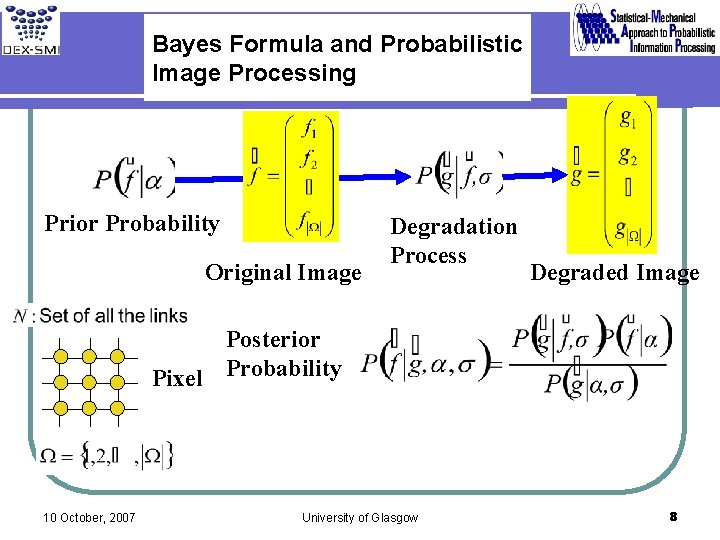
Bayes Formula and Probabilistic Image Processing Prior Probability Original Image Degradation Process Degraded Image Posterior Pixel Probability 10 October, 2007 University of Glasgow 8

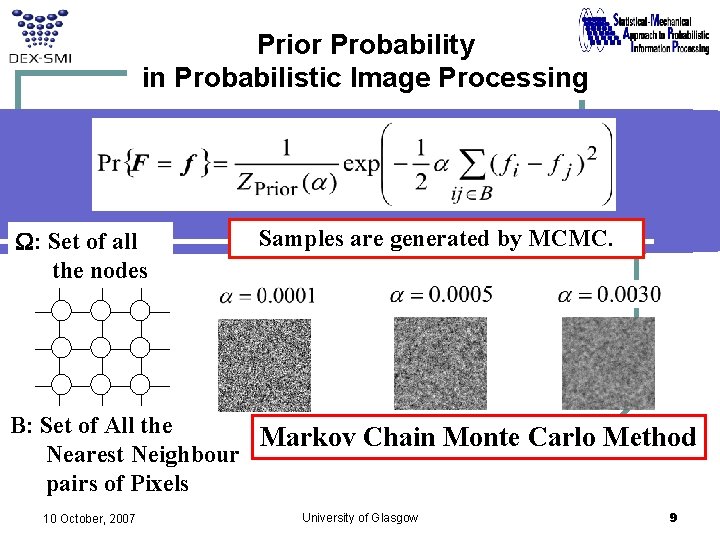
Prior Probability in Probabilistic Image Processing W: Set of all the nodes Samples are generated by MCMC. B: Set of All the Markov Chain Monte Carlo Method Nearest Neighbour pairs of Pixels 10 October, 2007 University of Glasgow 9

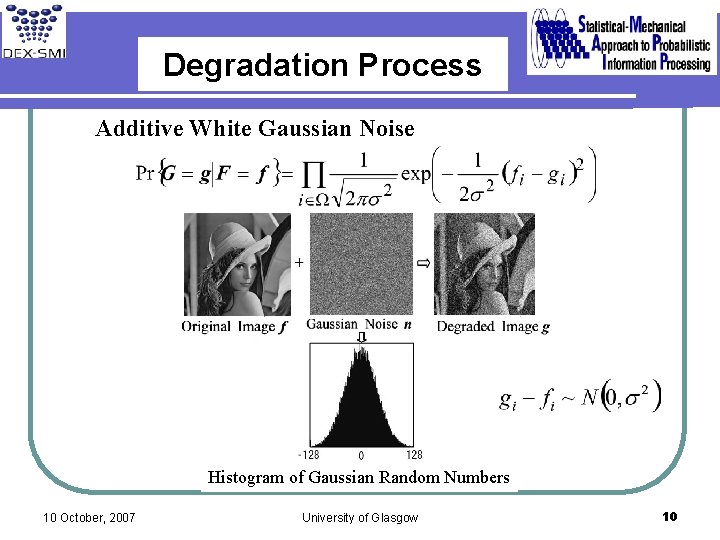
Degradation Process Additive White Gaussian Noise Histogram of Gaussian Random Numbers 10 October, 2007 University of Glasgow 10

Degradation Process and Prior Degradation Process Prior Probability Density Function Posterior Probability Density Function Multi-Dimensional Gaussian Integral Formula 10 October, 2007 University of Glasgow 11

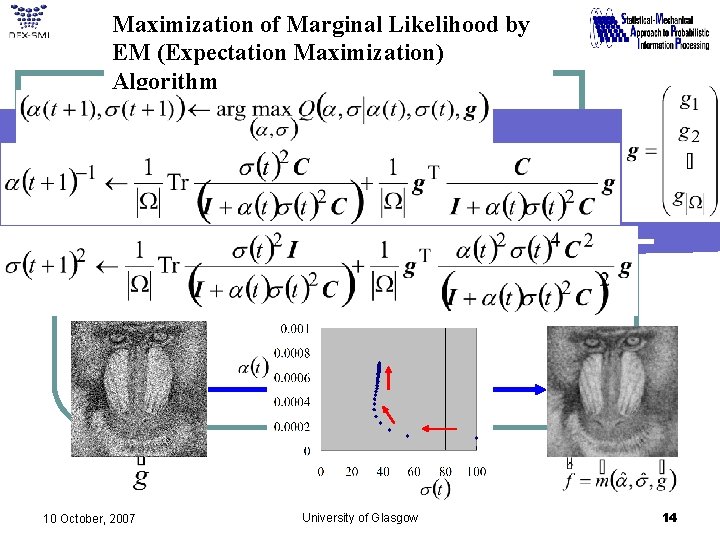
Maximization of Marginal Likelihood by EM Algorithm Marginal Likelihood Q-Function EM Algorithm Iterate the following EM-steps until convergence: A. P. Dempster, N. M. Laird and D. B. Rubin, “Maximum likelihood from incomplete data via the EM algorithm, ” J. Roy. Stat. Soc. B, 39 (1977). 10 October, 2007 University of Glasgow 12

Maximization of Marginal Likelihood by EM (Expectation Maximization) Algorithm Extremum Condisions of Q(a, s|a(t), s(t), g) w. r. t. a and s = 10 October, 2007 University of Glasgow 13

Maximization of Marginal Likelihood by EM (Expectation Maximization) Algorithm 10 October, 2007 University of Glasgow 14

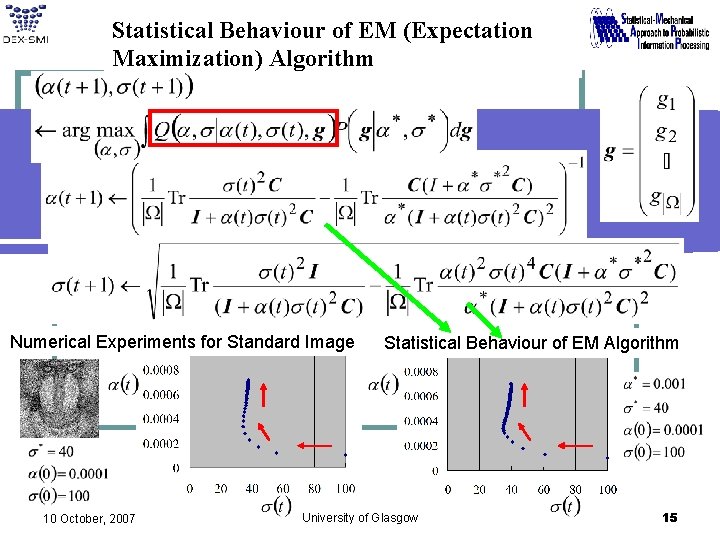
Statistical Behaviour of EM (Expectation Maximization) Algorithm Numerical Experiments for Standard Image 10 October, 2007 Statistical Behaviour of EM Algorithm University of Glasgow 15

Contents 1. 2. 3. 4. Introduction Gaussian Graphical Model and EM Algorithm Markov Chain Monte Carlo Method Concluding Remarks 10 October, 2007 University of Glasgow 16

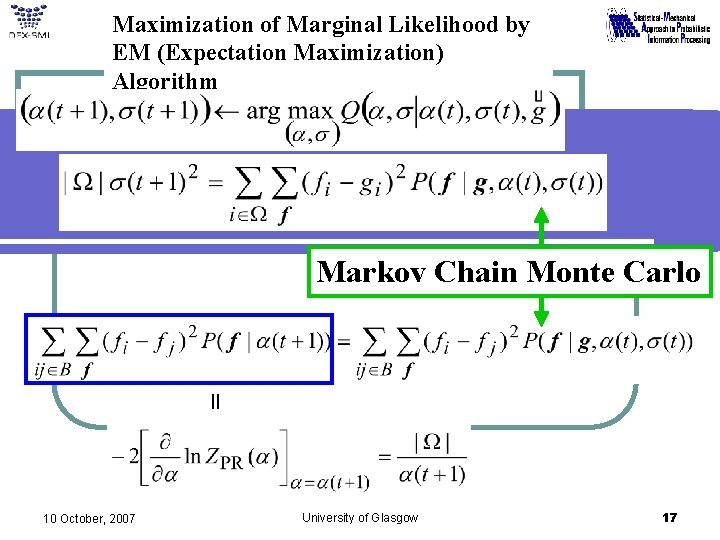
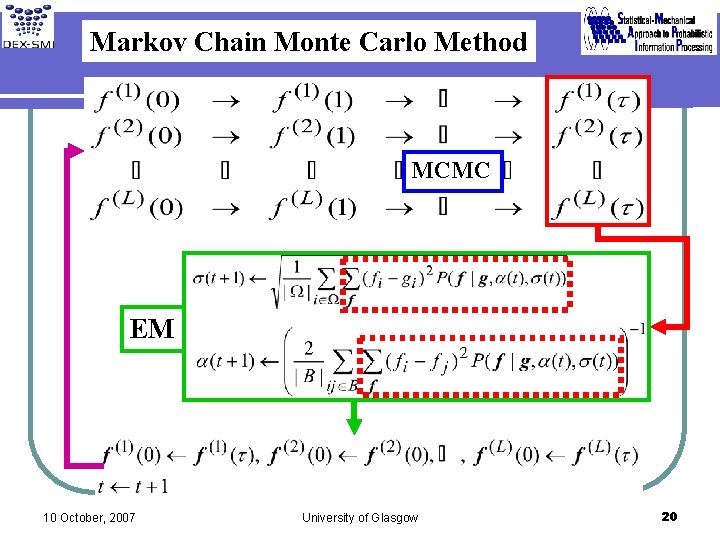
Maximization of Marginal Likelihood by EM (Expectation Maximization) Algorithm Markov Chain Monte Carlo = 10 October, 2007 University of Glasgow 17

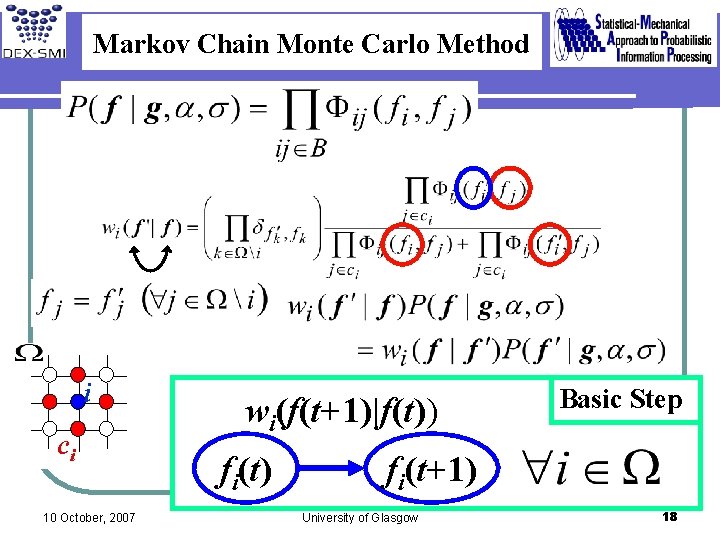
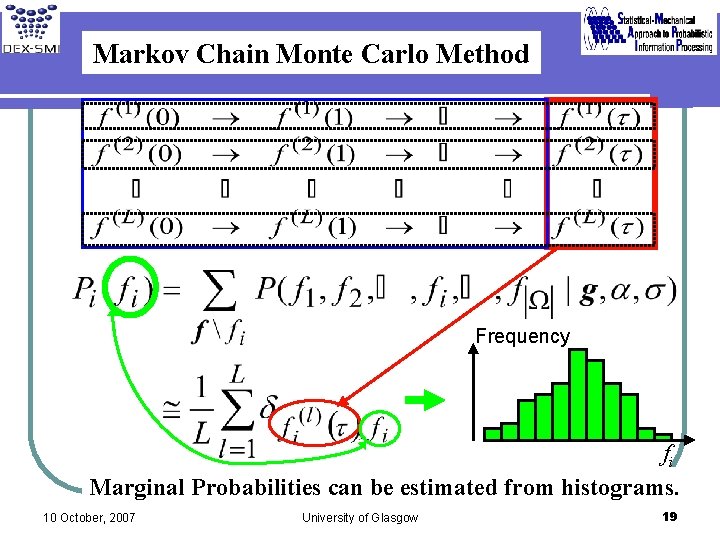
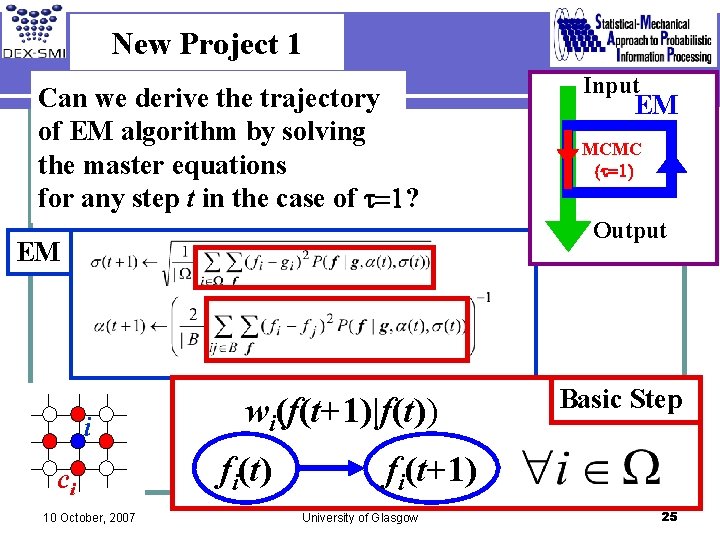
Markov Chain Monte Carlo Method i ci 10 October, 2007 wi(f(t+1)|f(t)) fi(t) Basic Step fi(t+1) University of Glasgow 18

Markov Chain Monte Carlo Method Frequency fi Marginal Probabilities can be estimated from histograms. 10 October, 2007 University of Glasgow 19

Markov Chain Monte Carlo Method MCMC EM 10 October, 2007 University of Glasgow 20

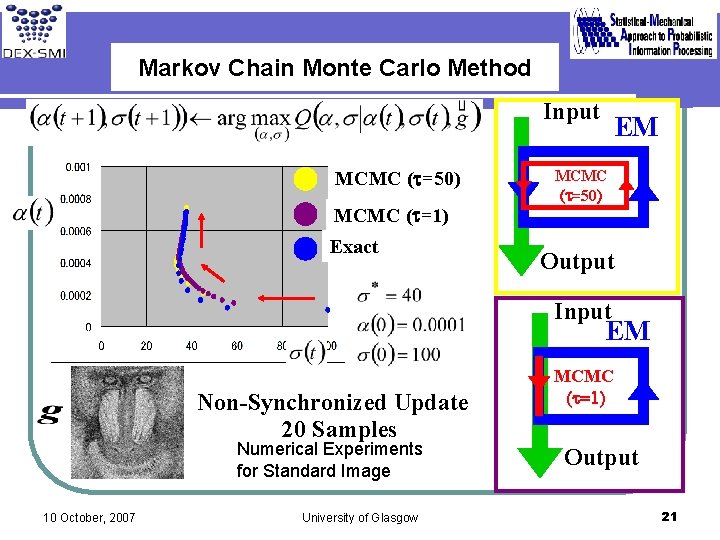
Markov Chain Monte Carlo Method Input MCMC (t=50) EM MCMC (t=50) MCMC (t=1) Exact Output Input EM Non-Synchronized Update 20 Samples Numerical Experiments for Standard Image 10 October, 2007 University of Glasgow MCMC (t=1) Output 21

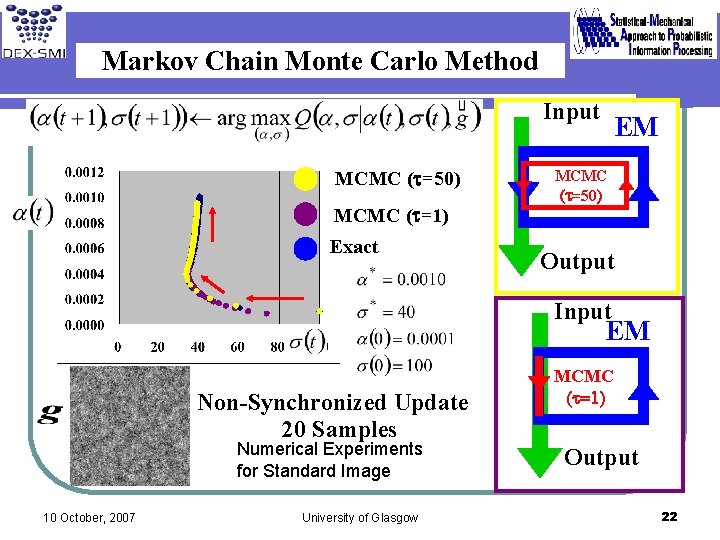
Markov Chain Monte Carlo Method Input MCMC (t=50) EM MCMC (t=50) MCMC (t=1) Exact Output Input EM Non-Synchronized Update 20 Samples Numerical Experiments for Standard Image 10 October, 2007 University of Glasgow MCMC (t=1) Output 22

Contents 1. 2. 3. 4. Introduction Gaussian Graphical Model and EM Algorithm Markov Chain Monte Carlo Method Concluding Remarks 10 October, 2007 University of Glasgow 23

Summary We construct EM algorithms by means of Markov Chain Monte Carlo method and compare them with some exact calculations. Input EM Input Exact Output 10 October, 2007 EM MCMC (t=50) Output University of Glasgow Input EM MCMC (t=1) Output 24

New Project 1 Can we derive the trajectory of EM algorithm by solving the master equations for any step t in the case of t=1? Input EM MCMC (t=1) Output EM i ci 10 October, 2007 wi(f(t+1)|f(t)) fi(t) Basic Step fi(t+1) University of Glasgow 25

New Project 1 Transition Probability From the solution of master equation, we calculate i ci 10 October, 2007 These are included in the EM update rules. University of Glasgow 26

New Project 2 Input Can we replace the calculation of statistical quantities in the prior probability by the MCMC? EM MCMC Output EM 10 October, 2007 University of Glasgow 27

New Project 3 Our previous works in EM algorithm and Loopy Belief Propagation K. Tanaka, H. Shouno, M. Okada and D. M. Titterington: J. Phys. A 2004 Hyperparameter Estimation by using Belief Propagation (BP) for Gaussian Graphical Model in Image Processing K. Tanaka and D. M. Titterington: J. Phys. A 2007 Statistical Trajectory of Approximate EM Algorithm for Probabilistic Image Processing 10 October, 2007 University of Glasgow 28

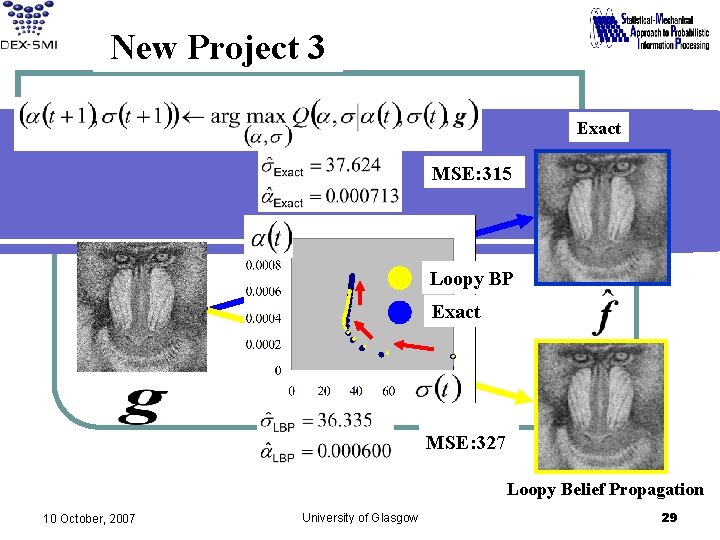
New Project 3 Exact MSE: 315 Loopy BP Exact MSE: 327 Loopy Belief Propagation 10 October, 2007 University of Glasgow 29

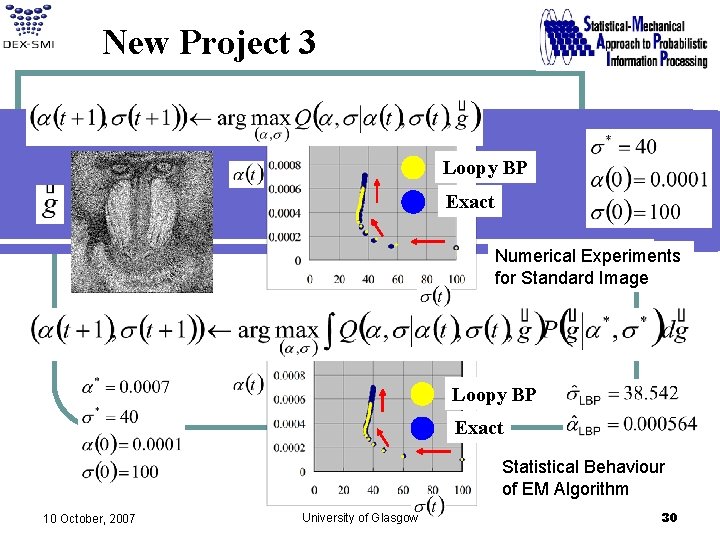
New Project 3 Loopy BP Exact Numerical Experiments for Standard Image Loopy BP Exact Statistical Behaviour of EM Algorithm 10 October, 2007 University of Glasgow 30

New Project 3 Can we update both messages and hyperparameters in the same step? Can we calculate the statistical trajectory? Input BP EM More Practical Algorithm BP EM Output 10 October, 2007 Input University of Glasgow 31