Ellipsometry Measures the amplitude and phase of reflected

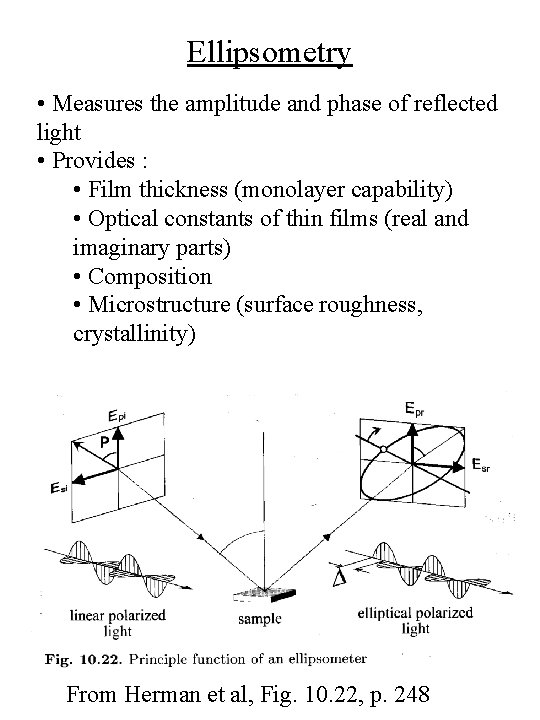
Ellipsometry • Measures the amplitude and phase of reflected light • Provides : • Film thickness (monolayer capability) • Optical constants of thin films (real and imaginary parts) • Composition • Microstructure (surface roughness, crystallinity) From Herman et al, Fig. 10. 22, p. 248

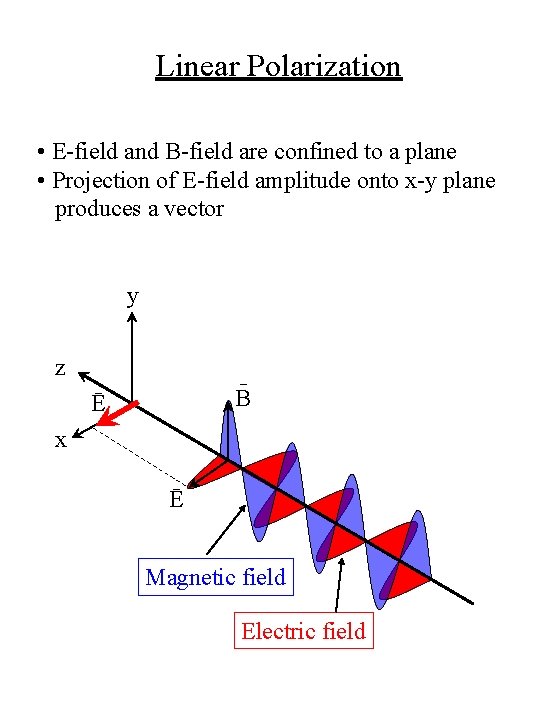
Linear Polarization • E-field and B-field are confined to a plane • Projection of E-field amplitude onto x-y plane produces a vector y z B Ē x Ē Magnetic field Electric field

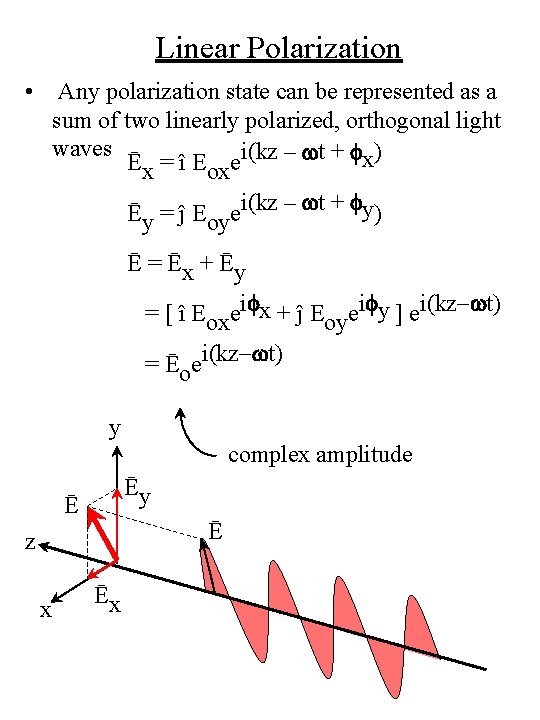
Linear Polarization • Any polarization state can be represented as a sum of two linearly polarized, orthogonal light waves Ēx = î Eoxei(kz – wt + fx) Ēy = ĵ Eoyei(kz – wt + fy) Ē = Ēx + Ēy = [ î Eoxeifx + ĵ Eoyeify ] ei(kz-wt) = Ēoei(kz-wt) y complex amplitude Ēy Ē Ē z x Ēx

Linear Polarization Ē = [ î Eoxeifx + ĵ Eoyeify ] ei(kz - wt) • Ēx and Ēy are in phase fx = fy y Ē z Ēy x Ēx

Ē = [ î Eoxeifx + ĵ Eoyeify ] ei(kz - wt) What if Ēx and Ēy are not in phase fx ≠ fy ? fy ≠ fx y Ēy z x Ēx

Elliptical Polarization Ē = [ î Eoxeifx + ĵ Eoyeify ] ei(kz - wt) • If Ēx and Ēy are not in phase Resultant Ē traces out an ellipse Elliptically polarized light y Resultant Ē w z x v

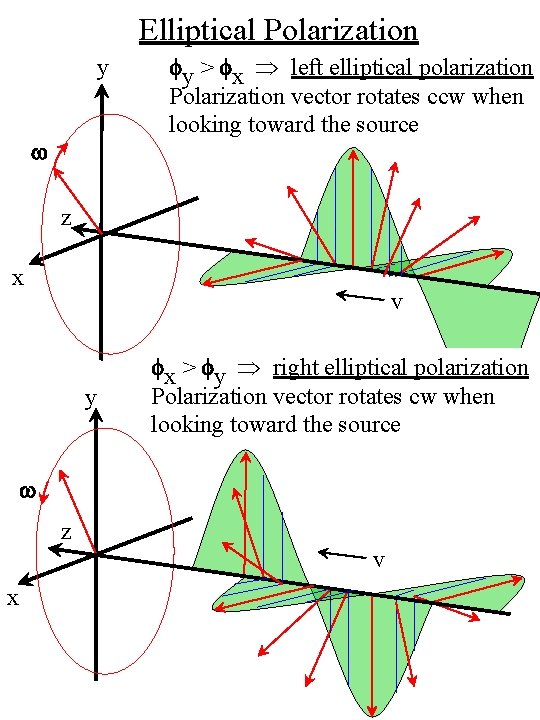
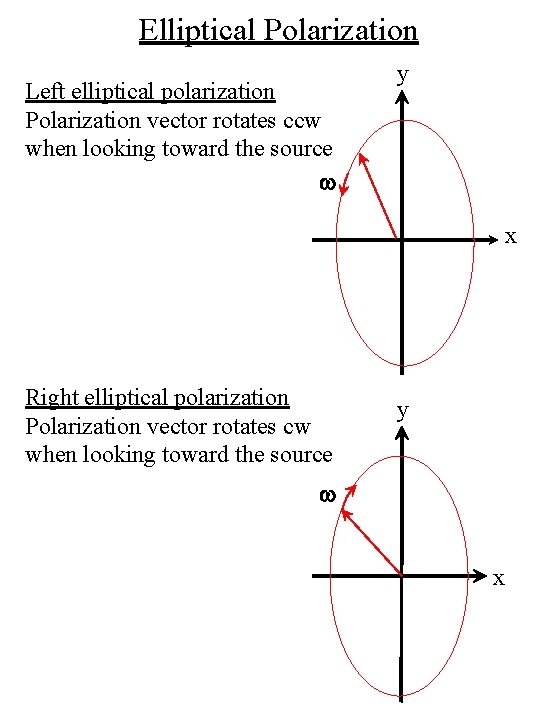
Elliptical Polarization y w fy > fx left elliptical polarization Polarization vector rotates ccw when looking toward the source z x v y fx > fy right elliptical polarization Polarization vector rotates cw when looking toward the source w z v x

Elliptical Polarization Left elliptical polarization Polarization vector rotates ccw when looking toward the source w y x Right elliptical polarization Polarization vector rotates cw when looking toward the source y w x

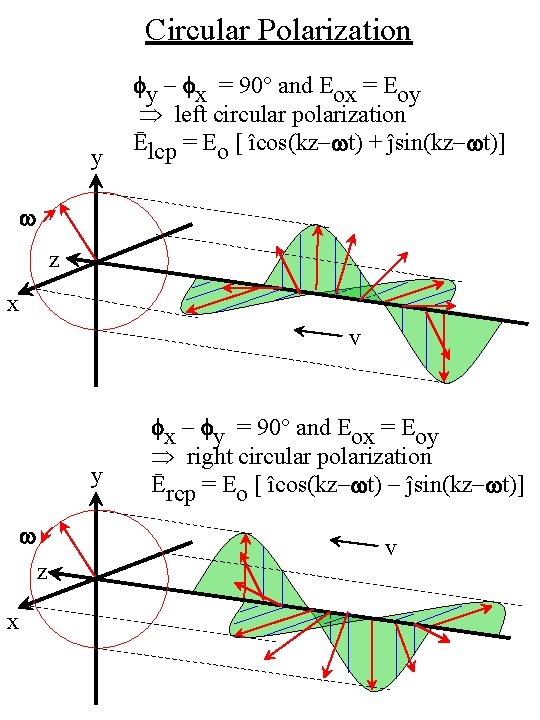
Circular Polarization y fy - fx = 90° and Eox = Eoy left circular polarization Ēlcp = Eo [ îcos(kz-wt) + ĵsin(kz-wt)] w z x v y w z x fx - fy = 90° and Eox = Eoy right circular polarization Ērcp = Eo [ îcos(kz-wt) - ĵsin(kz-wt)] v

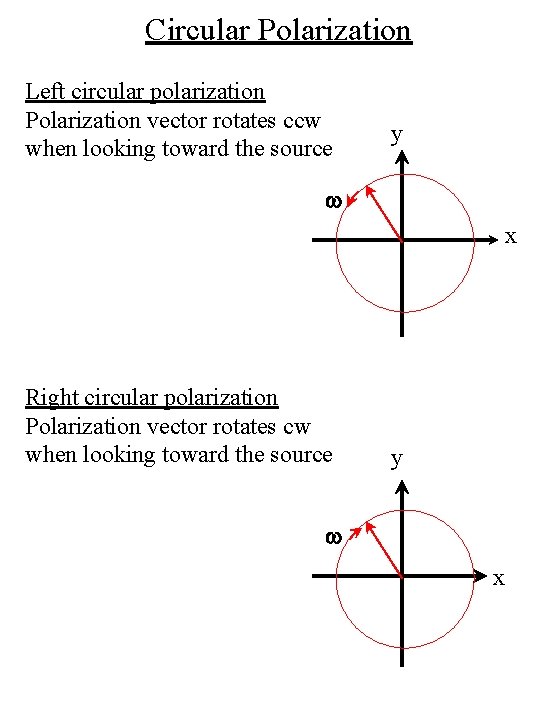
Circular Polarization Left circular polarization Polarization vector rotates ccw when looking toward the source y w x Right circular polarization Polarization vector rotates cw when looking toward the source y w x

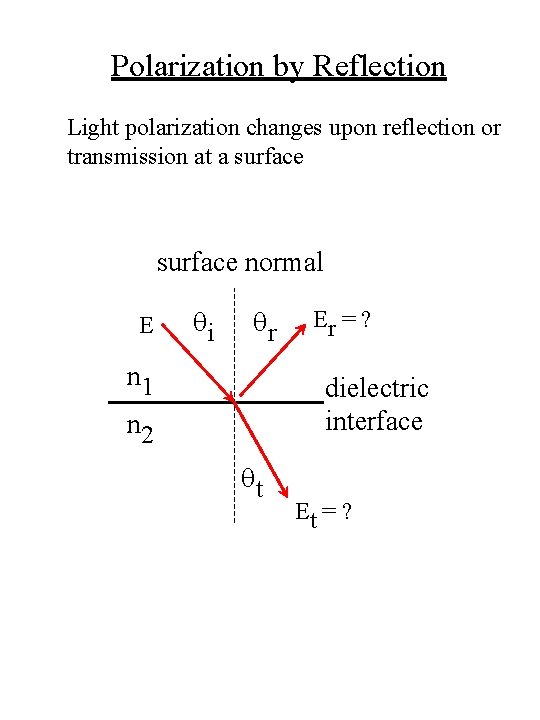
Polarization by Reflection Light polarization changes upon reflection or transmission at a surface normal E qi qr n 1 Er = ? dielectric interface n 2 qt Et = ?

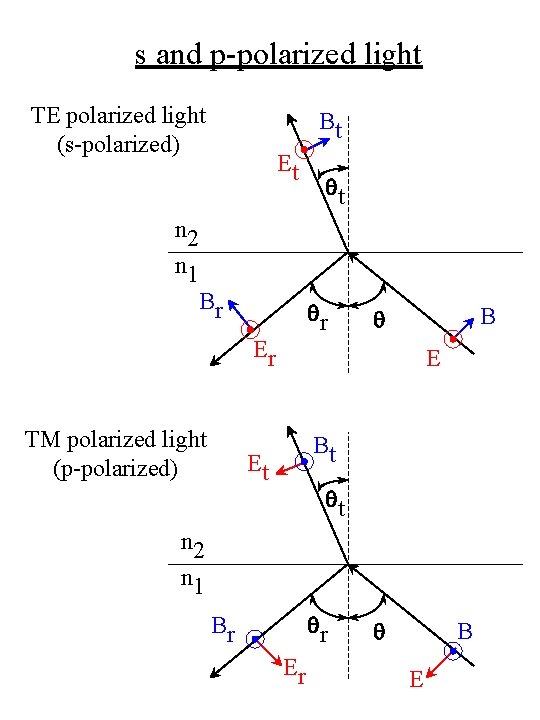
s and p-polarized light TE polarized light (s-polarized) Bt Et qt n 2 n 1 Br qr B q Er TM polarized light (p-polarized) E Bt Et qt n 2 n 1 qr Br Er q B E

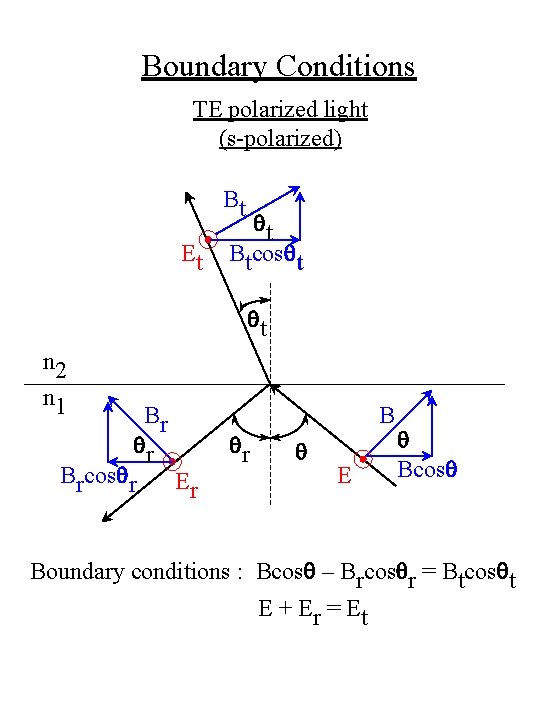
Boundary Conditions TE polarized light (s-polarized) Bt Et qt Btcosqt qt n 2 n 1 Br qr Brcosqr B qr Er q E q Bcosq Boundary conditions : Bcosq – Brcosqr = Btcosqt E + Er = E t

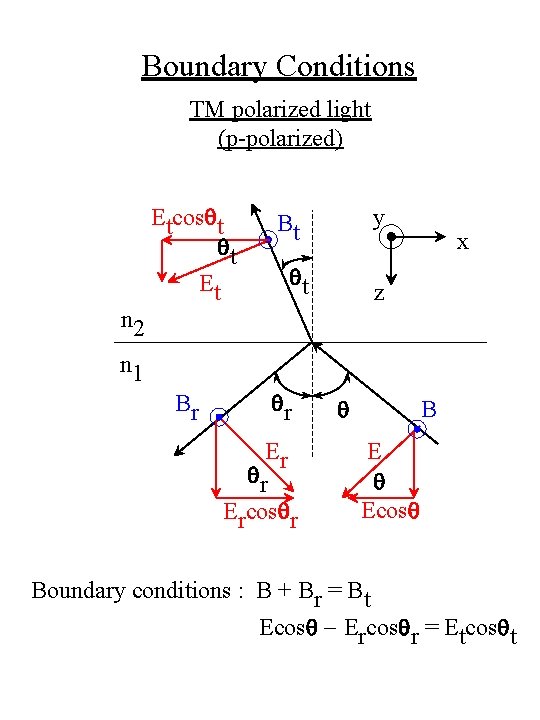
Boundary Conditions TM polarized light (p-polarized) Etcosqt qt Et Bt Br qr y qt x z n 2 n 1 Er qr Ercosqr q B E q Ecosq Boundary conditions : B + Br = Bt Ecosq - Ercosqr = Etcosqt

Fresnel Equations n = n 2/n 1 Reflection Coefficients: TE: r = Er / E = TM: r = Er / E = 2 – sin 2 q n cosq - √ 2 2 cosq + √ n – sin q 2 2 n 2 cosq - √ n – sin q 2 – sin 2 q 2 n n cosq + √ Transmission Coefficients: TE: t = Et / E = TM: t = Et / E = 2 cosq 2 – sin 2 q n cosq + √ 2 ncosq n 2 cosq + √ n 2 – sin 2 q

Reflectance and Transmittance Reflectance, R = Ir / I = (Er/E)2 = r 2 Transmittance, T = It / I = (n 2/n 1)(cosqt/cosqi) t 2 accounts for different rates of energy propagation accounts for different cross-sectional areas of incident and transmitted beams

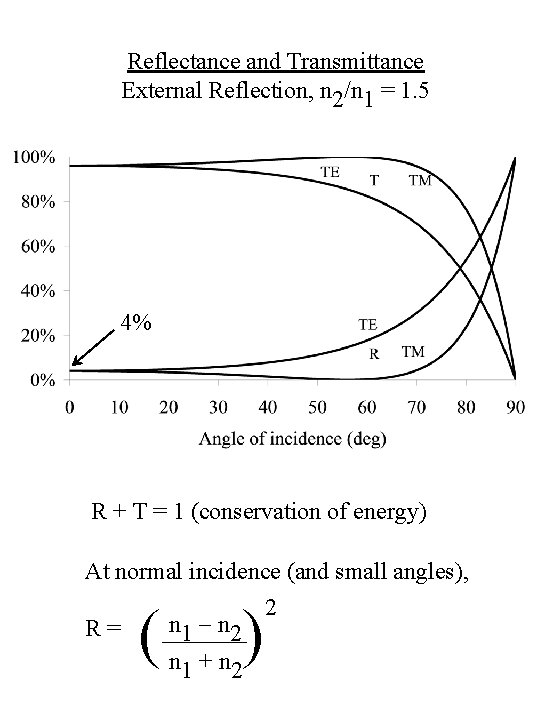
Reflectance and Transmittance External Reflection, n 2/n 1 = 1. 5 4% R + T = 1 (conservation of energy) At normal incidence (and small angles), 2 n 1 - n 2 R= n 1 + n 2 ( )

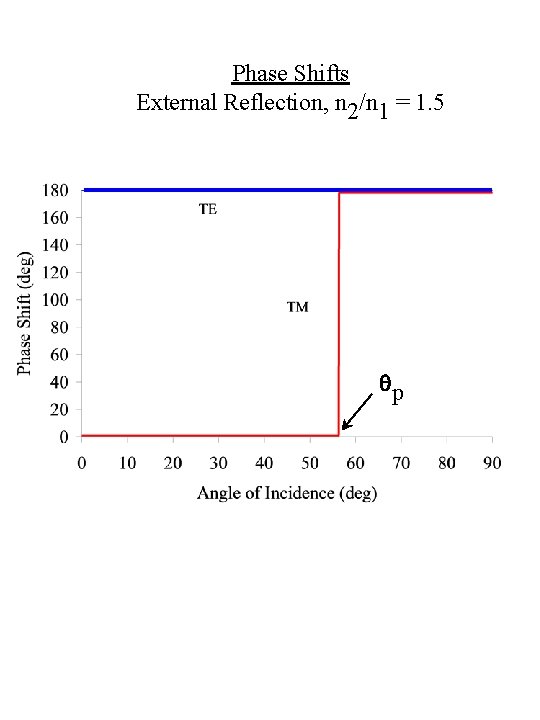
Phase Shifts External Reflection, n 2/n 1 = 1. 5 qp

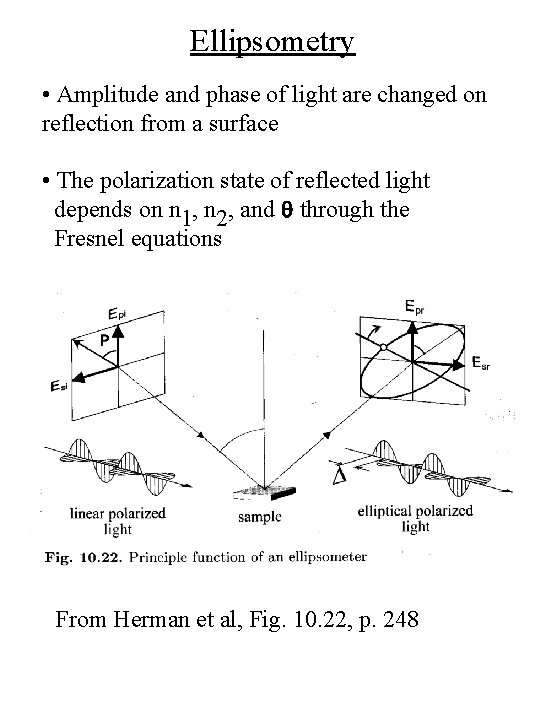
Ellipsometry • Amplitude and phase of light are changed on reflection from a surface • The polarization state of reflected light depends on n 1, n 2, and q through the Fresnel equations From Herman et al, Fig. 10. 22, p. 248

Ellipsometry • Ellipsometric parameters r = Rp / Rs = tan ei. D Rp = Ep (reflected) / Ep (incident) Rs = Es(reflected) / Es(incident) • Ellipsometry measures & D = tan-1(r) D = differential phase change = Dp - Ds • The Fresnel equations relate & D to the film thickness and optical constants • Ellipsometry is surface-sensitive due to ability to measure polarization extremely accurately (extinction ratios > 105 with polarizing prisms)

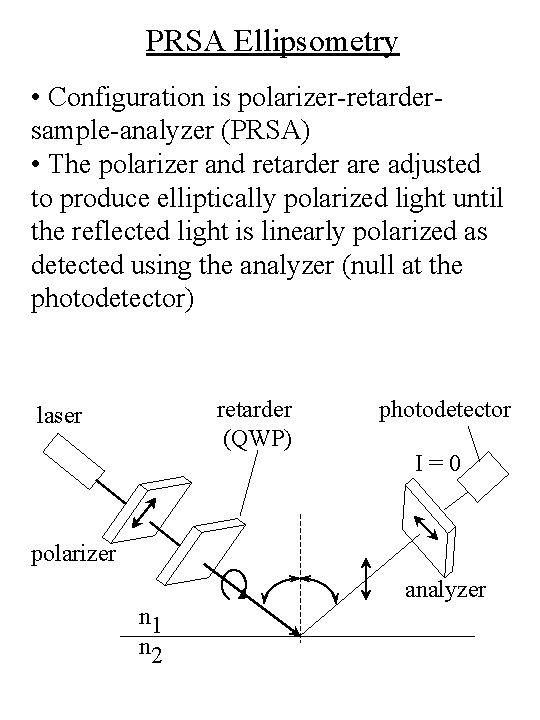
PRSA Ellipsometry • Configuration is polarizer-retardersample-analyzer (PRSA) • The polarizer and retarder are adjusted to produce elliptically polarized light until the reflected light is linearly polarized as detected using the analyzer (null at the photodetector) retarder (QWP) laser photodetector I=0 polarizer analyzer n 1 n 2

Ellipsometry • Penetration depth of light in semiconductors ~ mm’s • But ellipsometry has monolayer resolution. How? • Large dynamic range in intensity measurement (> 105 extinction ratio with polarizing prisms) • Use incident angle close to Brewster’s angle

VASE Ellipsometry Vary q and l to determine the optical constants of multilayer thin films laser l polarizer multilayer film retarder q photodetector q analyzer

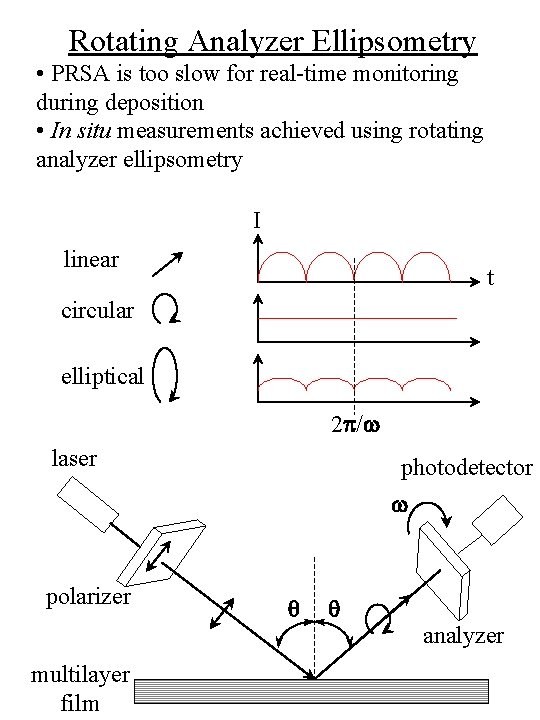
Rotating Analyzer Ellipsometry • PRSA is too slow for real-time monitoring during deposition • In situ measurements achieved using rotating analyzer ellipsometry I linear t circular elliptical 2 p/w laser photodetector w polarizer q q analyzer multilayer film

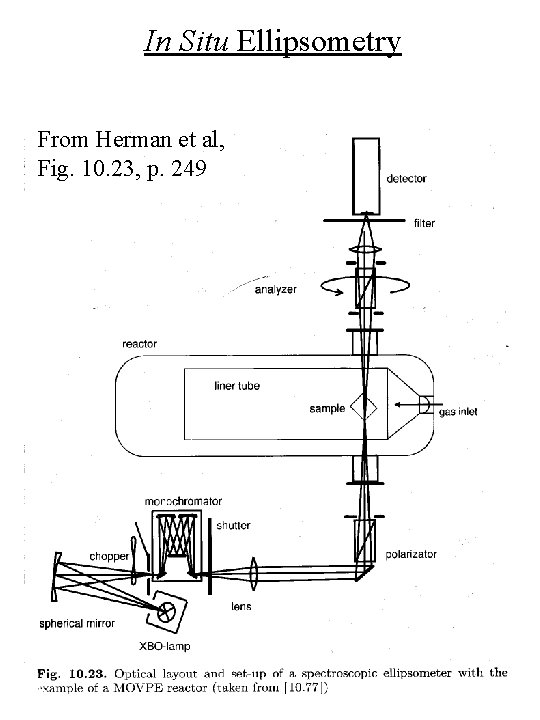
In Situ Ellipsometry From Herman et al, Fig. 10. 23, p. 249

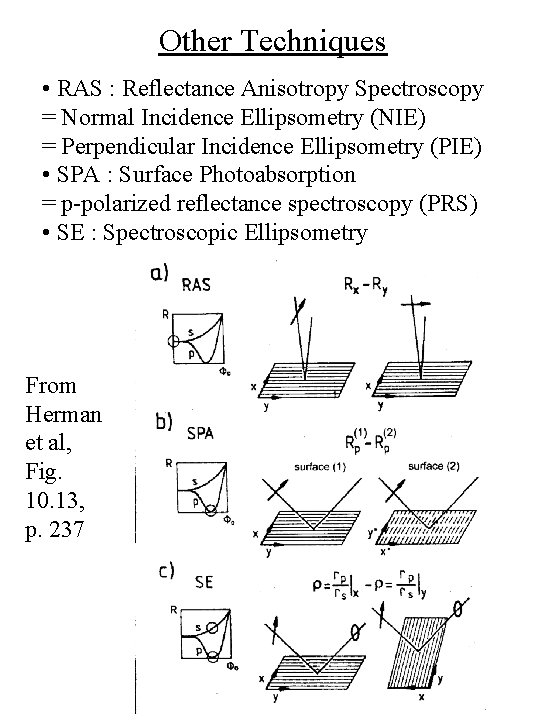
Other Techniques • RAS : Reflectance Anisotropy Spectroscopy = Normal Incidence Ellipsometry (NIE) = Perpendicular Incidence Ellipsometry (PIE) • SPA : Surface Photoabsorption = p-polarized reflectance spectroscopy (PRS) • SE : Spectroscopic Ellipsometry From Herman et al, Fig. 10. 13, p. 237

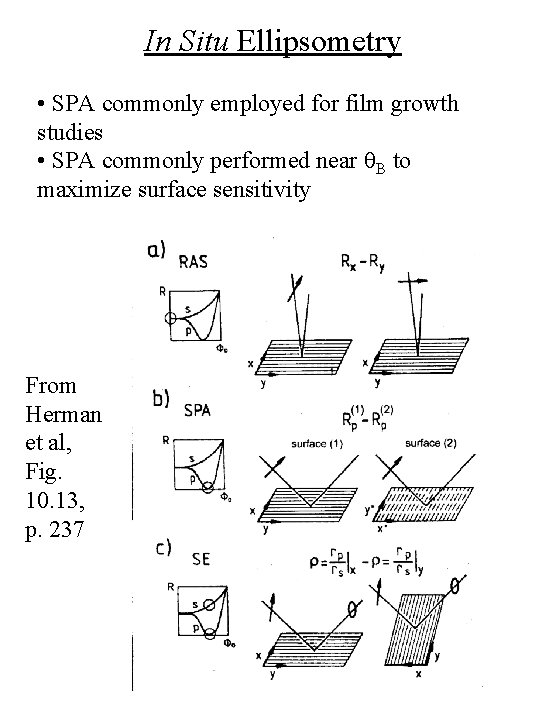
In Situ Ellipsometry • SPA commonly employed for film growth studies • SPA commonly performed near q. B to maximize surface sensitivity From Herman et al, Fig. 10. 13, p. 237

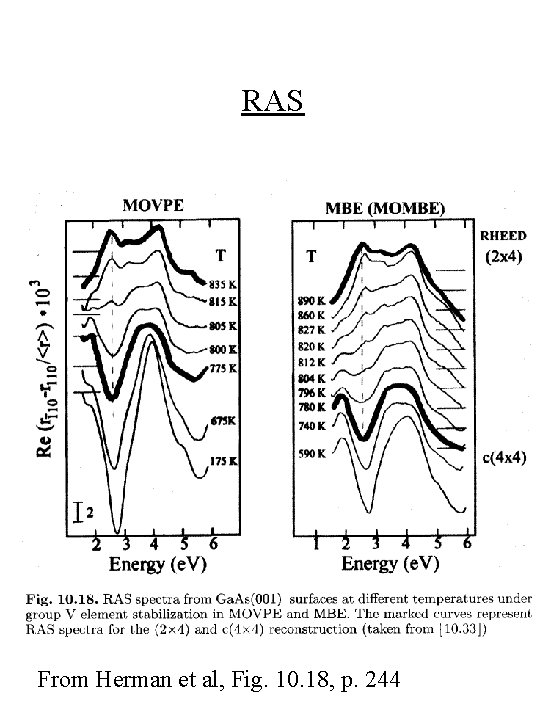
RAS From Herman et al, Fig. 10. 18, p. 244

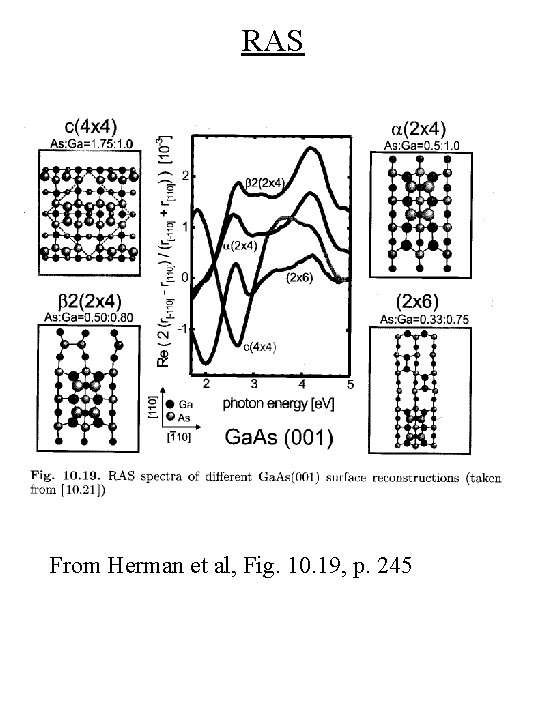
RAS From Herman et al, Fig. 10. 19, p. 245