Elevator algorithms and the DialaRide problem Mathematical Foundations

Elevator algorithms and the Dial-a-Ride problem Mathematical Foundations of AI Reshef Meir

A basic elevator algorithm • Consider the following Algorithm QUEUE for elevators: • Every new call enters a queue • Calls are served in order of arrival • Calls are served on the way if possible ()

A basic elevator algorithm • Consider the following Algorithm QUEUE for elevators: • Every new call enters a queue • Calls are served in order of arrival • Calls are served on the way if possible 5 6 ( (3 6) )

A basic elevator algorithm • Consider the following Algorithm QUEUE for elevators: • Every new call enters a queue • Calls are served in order of arrival • Calls are served on the way if possible 5 ( (3 6) , (4 5)) 5

A basic elevator algorithm • Consider the following Algorithm QUEUE for elevators: • Every new call enters a queue • Calls are served in order of arrival • Calls are served on the way if possible ( (3 6) , (4 5), (2 5)) 5 5

A basic elevator algorithm • Consider the following Algorithm QUEUE for elevators: 6 • Every new call enters a queue • Calls are served in order of arrival • Calls are served on the way if possible ( (3 6) , (2 5)) 5

A basic elevator algorithm • Consider the following Algorithm QUEUE for elevators: • Every new call enters a queue • Calls are served in order of arrival • Calls are served on the way if possible ( (2 5)) 5

A basic elevator algorithm • Consider the following Algorithm QUEUE for elevators: • Every new call enters a queue • Calls are served in order of arrival • Calls are served on the way if possible • Is this a good algorithm? 5

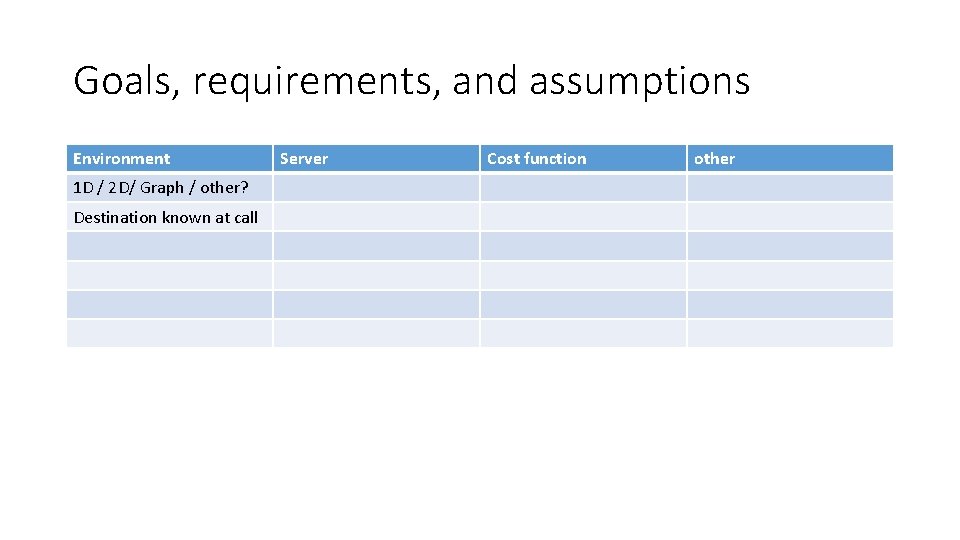
Goals, requirements, and assumptions Environment 1 D / 2 D/ Graph / other? Destination known at call Server Cost function other

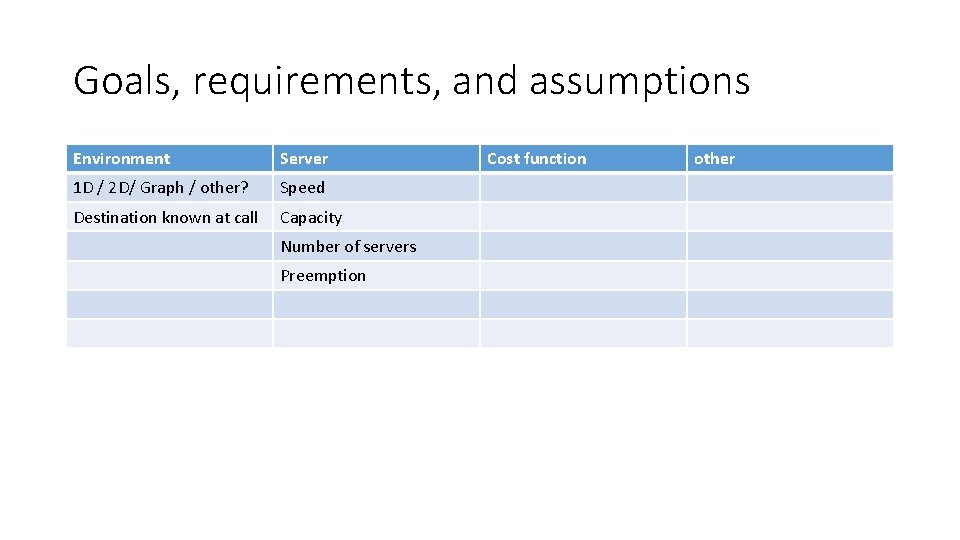
Goals, requirements, and assumptions Environment Server 1 D / 2 D/ Graph / other? Speed Destination known at call Capacity Number of servers Preemption Cost function other

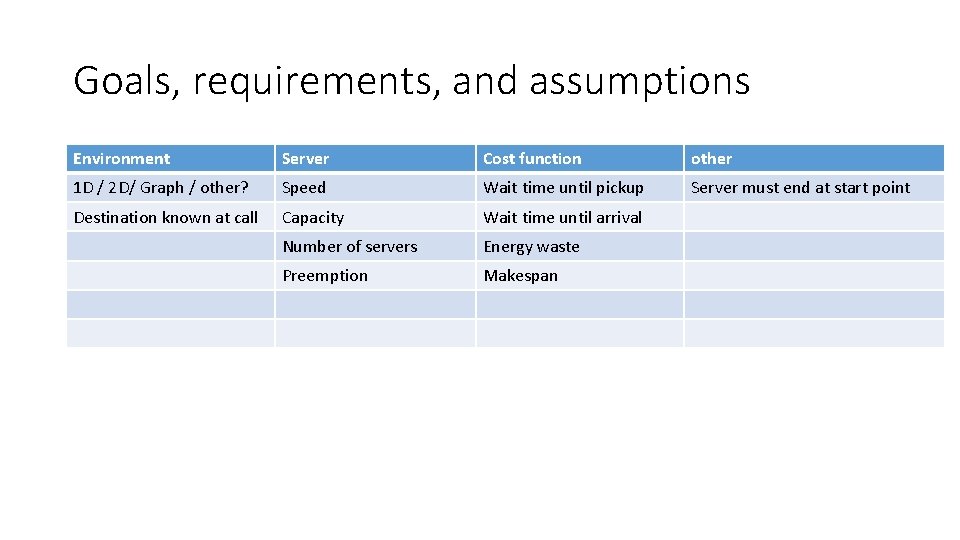
Goals, requirements, and assumptions Environment Server Cost function other 1 D / 2 D/ Graph / other? Speed Wait time until pickup Server must end at start point Destination known at call Capacity Wait time until arrival Number of servers Energy waste Preemption Makespan

Some definitions • An instance is a sequence of calls ri = (ti, ai, bi) • ti is the time of call • ai is the pickup location • bi is the destination (may only be revealed after pickup) • J = (r 1, r 2, r 3, … , rm) • The quality of algorithm A on instance J, is the time required to • Start in the origin O • complete all tasks • return to O

Competitive Ratio • OPT(J) is the minimal time (makespan) it would take for a “perfect” server that knows all the tasks in advance • We compare each algorithm A to the optimal algorithm OPT CR(A) = max. J {A(J) / OPT(J)} • Similar to approximation ratio • not due to computational complexity, but due to lack of information

Analyzing the competitive ratio • How good (or bad) is the QUEUE algorithm ? • Does an optimal algorithm exist?

The IGNORE algorithm (Lipmann et al. 04) • We assume complete information • Loop: • Wait until S ≠ empty • Plan optimal route DAR(S) • Perform DAR(S) • (ignore new requests) • Update S after returning O * • S= ()

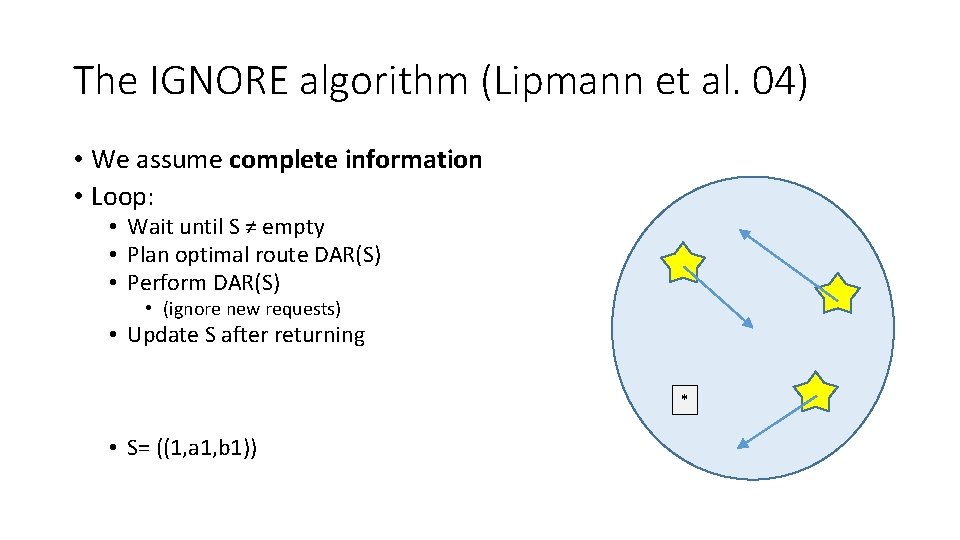
The IGNORE algorithm (Lipmann et al. 04) • We assume complete information • Loop: • Wait until S ≠ empty • Plan optimal route DAR(S) • Perform DAR(S) • (ignore new requests) • Update S after returning O * • S= ((1, a 1, b 1))

The IGNORE algorithm (Lipmann et al. 04) • We assume complete information • Loop: • Wait until S ≠ empty • Plan optimal route DAR(S) • Perform DAR(S) • (ignore new requests) • Update S after returning O * • S= ((1, a 1, b 1)) • S= ((3, a 2, b 2); (5, a 3, b 3))

The SNIFFER algorithm (Ascheuer et al. ‘ 00) We assume partial information (bi is revealed at pickup) 1. Repeat (wait): If a new task arrives, compute an optimal TSP(S) 2. Until t ≥ |TSP(S)| and S ≠ empty 3. Execute TSP(S) ; R S; update S 4. If S≠ empty, goto (1) 5. Compute an optimal DAR(R) 6. Repeat (wait) If a new task arrives (S≠ empty), goto (1) 7. Until t ≥ |DAR(R)| 8. Execute DAR(R); R empty; update S 9. Goto (1) S = tasks with unknown goal R = (unserved) tasks with known goal t = current time TSP = Traveling Sales Person (only visit) DAR = Dial-a-Ride (serve tasks)