Elementi di logica matematica Prof Ugo Morra Programma

Elementi di logica matematica. Prof. Ugo Morra Programma Operativo Nazionale Scuola “Competenze per lo sviluppo” Fondo sociale europeo 2009/2010 Liceo scientifico R. Nuzzi di Andria Matematica: si grazie!

Logica nelle … frasi comuni. Qual è la negazione della frase Luca ha almeno due figli? RISPOSTA. Luca ha al più un figlio (o ha un solo figlio o non ce ne ha nessuno!)

Logica nelle … frasi comuni. Qual è la negazione della frase Ogni studente della II A ha l’orologio? RISPOSTA. Esiste almeno uno studente di II A che non ha l’orologio.

Logica nelle … frasi comuni. Qual è la negazione della frase Ogni studente della V A ha almeno due cugini ? RISPOSTA. Esiste almeno uno studente di VA che ha al più un cugino.

100 delegati sono riuniti in congresso. Non tutti portano la cravatta, ma si sa che comunque se ne scelgano due, almeno uno dei due la porta. Quanti sono i congressisti con cravatta? • Almeno 2, ma possono essere meno di 50 • Esattamente 50 • più di 50, ma non si può dire esattamente quanti • la situazione descritta è impossibile • Nessuna delle precedenti affermazioni è vera

Definizione di logica La logica (dal greco logiké, riguardante il parlare o il ragionare) è lo studio del ragionamento. La logica matematica è lo studio dei ragionamenti utilizzati dai matematici e pertanto si occupa dei linguaggi formali quelli in cui non vi sono né ambiguità di interpretazione, né eccezioni alle regoleintroducendo regole che garantiscono la correttezza dei ragionamenti.

Enunciati Si dice enunciato o proposizione, un’espressione linguistica cui sia possibile attribuire un valore di “vero” (simbolo V oppure 1) o di falso (simbolo F oppure 0). Il cane è un quadrupede. 27 è il cubo di 3. Il serpente è un mammifero. 35 è un numero pari.

Le prime due affermazioni sono vere, mentre le altre sono false. In ogni caso le affermazioni precedenti sono tutte degli enunciati (o proposizioni). Ad ogni enunciato si può associare uno solo dei due valori di verità Vero V Falso F

Per indicare un enunciato si usano le lettere minuscole. p: seguo il corso “Matematica: si grazie!” Un enunciato è atomico (o semplice) se non è suddivisibile in altri più elementari. Gli enunciati visti prima sono tutti semplici.

Enunciati composti Un enunciato composto è quello in cui più enunciati semplici sono legati dai connettivi …e… …o… se…allora… …se e solo se…

ESEMPIO p: studio latino q: vado al teatro Con tali enunciati possiamo formare, ad esempio, i seguenti altri enunciati: a: studio latino e vado al teatro b: studio latino o vado al teatro c: se studio latino allora vado al teatro d: studio latino se e solo se vado al teatro

Dunque un connettivo logico è un operatore che trasforma due enunciati elementari in un nuovo enunciato composto. IDEA: Con i connettivi si possono effettuare delle operazioni tra gli enunciati semplici. Esse sono dette operazioni logiche.

Per eseguire queste operazioni e visualizzarne il risultato ci si serve delle tavole di verità.

2) Congiunzione: se p, q sono proposizioni, la proposizione p q è la loro congiunzione, con la seguente tavola di verità: p q p q ----------- V V V F F Condizione: p q è Vera se e solo se sia p che q sono Vere.

3) Disgiunzione: se p, q sono proposizioni, la proposizione p q è la loro disgiunzione, con la seguente tavola di verità: p q p q -----------V V V F V V F F Condizione: p q è Vera se p è Vera oppure q è Vera o entrambe sono Vere. p q è Falsa se e solo se sia p che q sono False.

4) Implicazione di due enunciati: se p, q sono proposizioni, si definisce p q (leggi: p implica q, se p allora q, da p segue q) come l’enunciato che è falso nel caso in cui p sia vero e q sia falso ed è vero in tutti gli altri casi. p: antecedente; q: conseguente. Con la tavola di verità: p q p q ---------- V V F F F V V F F V

Esempi Consideriamo gli enunciati: p: 12 è divisibile per 4 q: 12 è un numero pari L’enunciato p q risulterà vero ed è Se 12 è divisibile per 4 allora 12 è un numero pari

(5) Equivalenza (o coimplicazione ): se p, q sono proposizioni, l'equivalenza p q (p se e solo se q) è una proposizione, con la seguente tavola di verità: p q ---------- V V V F F V F F F V Condizione: p q è Vera se e solo se p e q sono entrambe Vere, o entrambe False.

Negazione di un enunciato Si definisce negazione di un enunciato p e si indica con l’enunciato che è falso se p è vero ed è vero se p è falso.

Leggi di De Morgan

Modus Ponens MP A B due premesse A __________

Esempi di Modus Ponens • Se Giorgio è un deputato, vive a Roma. • Giorgio è un deputato • Quindi, Giorgio vive a Roma • Se non piove, allora esco. • Non piove. • Quindi esco. • Se è sabato o domenica, vado a teatro. • E' sabato o domenica. •

Modus Tollens MT A B due premesse ~ B _____________ __ ~ A una conclusione

Esempi Modus Tollens • Se Marco ha perso il treno, è rimasto a casa. • Marco non ha perso il treno. • Se non fa freddo, non metto il cappotto. • Metto il cappotto. • Quindi fa freddo. • Se ho studiato poco, non passo l'esame. • Passo l'esame. • Non ho studiato poco (i. e. ho studiato molto).

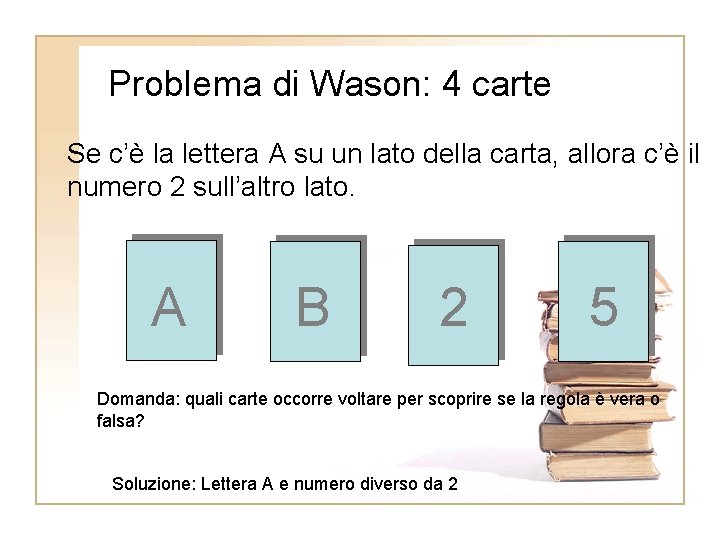
Problema di Wason: 4 carte Se c’è la lettera A su un lato della carta, allora c’è il numero 2 sull’altro lato. A B 2 5 Domanda: quali carte occorre voltare per scoprire se la regola è vera o falsa? Soluzione: Lettera A e numero diverso da 2